6.3: El desarrollo de la teoría cuántica
- Page ID
- 1847
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Extender el concepto de dualidad onda-partícula que se observó en la radiación electromagnética a la materia también
- Comprender la idea general de la descripción mecánica cuántica de los electrones en un átomo y que usar la noción de funciones de onda tridimensionales, u orbitales, que definen la distribución de probabilidad para encontrar un electrón en una parte particular del espacio.
- Enumerar y describir los rasgos de los cuatro números cuánticos que forman la base para especificar completamente el estado de un electrón en un átomo
El modelo de Bohr explicó los datos experimentales para el átomo de hidrógeno y fue ampliamente aceptado, pero también planteó muchas preguntas. ¿Por qué los electrones orbitaron a distancias fijas definidas por un solo número cuántico n = 1, 2, 3, etc., pero nunca en el medio? ¿Por qué el modelo funcionó tan bien describiendo hidrógeno e iones de un electrón, pero no pudo predecir correctamente el espectro de emisión para el helio o cualquier otro átomo más grande? Para responder a estas preguntas, los científicos necesitaban revisar completamente la forma en que pensaban sobre la materia.
El comportamiento en el mundo microscópico
Sabemos cómo se comporta la materia en el mundo macroscópico: los objetos que son lo suficientemente grandes para ser vistos a simple vista siguen las reglas de la física clásica. Una bola de billar que se mueve sobre una mesa se comportará como una partícula: continuará en una línea recta si no colisiona con otra bola o con el cojín de la mesa, o sea accionada por alguna otra fuerza (como la fricción). La bola tiene una posición y velocidad bien definida (o un momento bien definido, p = mv, definido por la masa m y la velocidad v) en cualquier momento dado. En otras palabras, la pelota se mueve en una trayectoria clásica. Este es el comportamiento típico de un objeto clásico.
Cuando las ondas interactúan entre sí, muestran patrones de interferencia que no son mostrados por partículas macroscópicas como la bola de billar. Por ejemplo, las olas que interactúan en la superficie del agua pueden producir patrones de interferencia similares a los que se muestran en la Figura \(\PageIndex{1}\). Este es un caso de comportamiento de onda en la escala macroscópica, y está claro que las partículas y las ondas son fenómenos muy diferentes en el ámbito macroscópico.

A medida que la tecnología permitió a los científicos explorar el mundo microscópico con mayor detalle, en la década de 1920 se hizo cada vez más evidente que piezas muy pequeñas de materia siguen un conjunto diferente de reglas de las que observamos para objetos grandes. La indiscutible separación de las ondas y las partículas ya no era el caso del mundo microscópico.
Una de las primeras personas en prestar atención al comportamiento especial del mundo microscópico fue Louis de Broglie. Él hizo la pregunta: Si la radiación electromagnética puede tener un carácter similar a una partícula, ¿Pueden los electrones y otras partículas submicroscópicas exhibir un carácter similar a una onda? En su disertación doctoral del año 1925, De Broglie extendió la dualidad de la onda-partícula de la luz que Einstein usó para resolver la paradoja del efecto fotoeléctrico a las partículas materiales. Predijo que una partícula con masa m y velocidad v (es decir, con momento lineal p) también debería mostrar el comportamiento de una onda con un valor de longitud de onda λ, dada por esta expresión en la que h es el constante de Planck.
\[\lambda=\dfrac{h}{mv}=\dfrac{h}{p} \label{6.4.1}\]
Esto se llama la longitud de onda de De Broglie. A diferencia de los otros valores de λ descritos en este capítulo, la longitud de la onda de De Broglie es una característica de las partículas y otros cuerpos, no de la radiación electromagnética (tenga en cuenta que esta ecuación involucra la velocidad [v, m / s], no la frecuencia [ν, Hz]. Aunque estos dos símbolos son idénticos, significan cosas muy diferentes). Cuando Bohr había postulado que el electrón era una partícula que orbita alrededor del núcleo en órbitas cuantificadas, De Broglie argumentó que la suposición de cuantificación de Bohr se puede explicar si el electrón no se considera como una partícula, sino más bien como una onda estacionaria circular tal que solo un entero El número de longitudes de onda podría caber exactamente dentro de la órbita (Figura \(\PageIndex{2}\)).
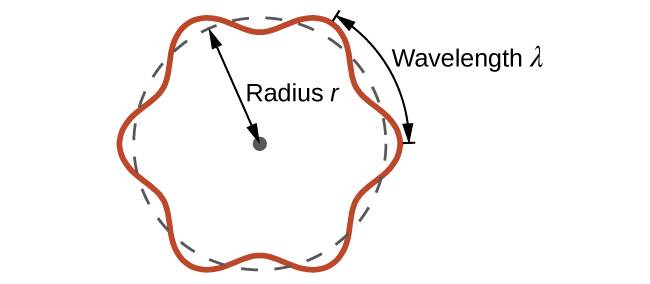
Para una órbita circular de radio r, la circunferencia es 2πr, por lo que la condición de De Broglie es:
\[2πr=nλ \label{6.4.3}\]
con \(n=1,2,3,...\)
Dado que la expresión de Broglie relaciona la longitud de la onda con el impulso y, por lo tanto, con la velocidad, esto implica:
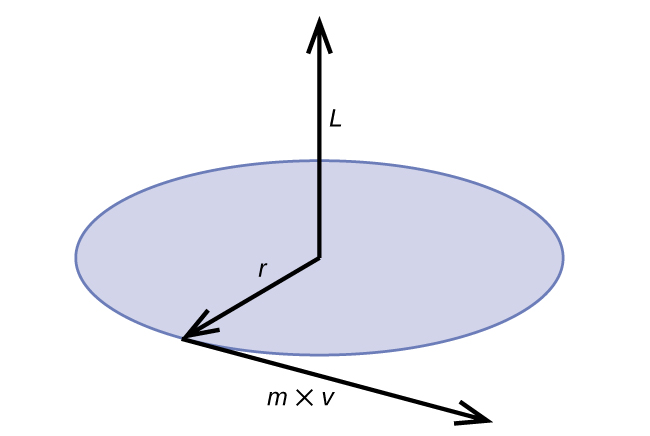
\[2πr=nλ=\dfrac{nh}{p}=\dfrac{nh}{mv}=\dfrac{nhr}{mvr}=\dfrac{nhr}{L} \label{6.4.3b}\]
Esta expresión se puede reorganizar para dar la farmula de Bohr para la cuantización del momento angular:
\[L=\dfrac{nh}{2π}=n \hbar \label{6.4.4}\]
El momento angular clásico L para un movimiento circular es igual al producto del radio del círculo y al momento de la partícula en movimiento p.
\[L=rp=rmv \;\;\; \text{(for a circular motion)} \label{6.4.5}\]
Poco después de que De Broglie propusiera la naturaleza ondulatoria de la materia, dos científicos de los Laboratorios Bell, C. J. Davisson y L. H. Germer, demostraron experimentalmente que los electrones pueden demostrar un comportamiento de onda al mostrar un patrón de interferencia para los electrones que viajan a través de un patrón atómico regular en un cristal. Las capas atómicas espaciadas regularmente sirvieron como rendijas, como se usa en otros experimentos de interferencia. Dado que el espaciado entre las capas que sirven como rendijas debe ser similar en tamaño a la longitud de onda de la onda probada para que se forme un patrón de interferencia, Davisson y Germer usaron un objetivo de níquel cristalino para sus "rendijas", ya que el espaciado de los átomos dentro de la celosía era aproximadamente la misma que la longitud de onda de Broglie de los electrones que utilizaban. La figura \(\PageIndex{4}\) muestra un patrón de interferencia.
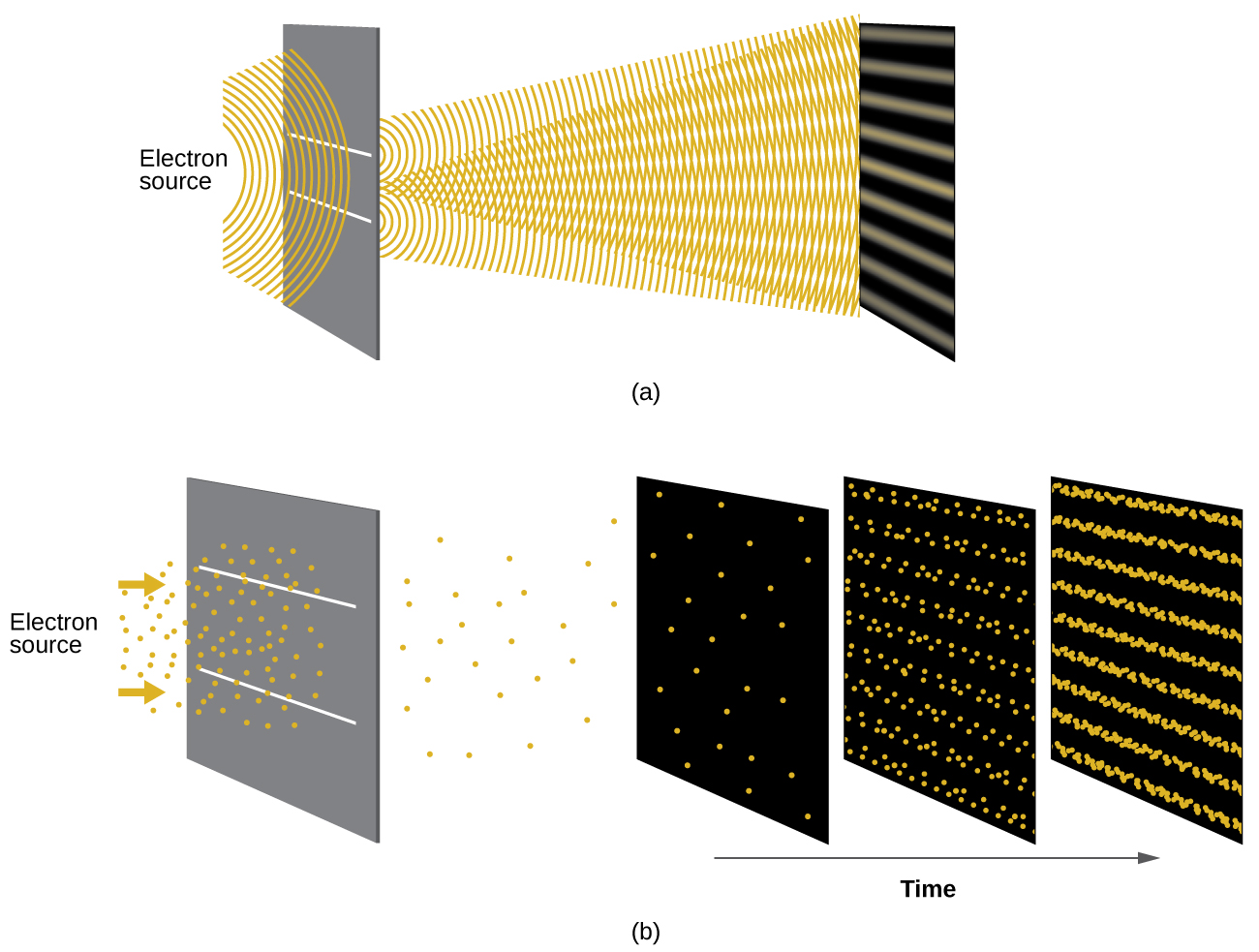
La dualidad de la onda-partícula de la materia se puede ver observando lo que sucede si las colisiones de electrones se registran durante un largo período de tiempo. Inicialmente, cuando solo se han registrado unos pocos electrones, muestran un claro comportamiento similar a las partículas, habiendo llegado en pequeños paquetes localizados que parecen ser aleatorios. A medida que más y más electrones llegaron y se registraron, surgió un claro patrón de interferencia que es el sello distintivo del comportamiento de la onda. Por lo tanto, parece que los electrones son pequeñas partículas localizadas, su movimiento no sigue las ecuaciones de movimiento implícitas en la mecánica clásica, sino que se rige por algún tipo de ecuación de onda que gobierna una distribución de probabilidad incluso para el movimiento de un solo electrón. Por lo tanto, la dualidad de onda-partícula observada por primera vez con los fotones es en realidad un comportamiento fundamental intrínseco a todas las partículas cuánticas.
Vea el dibujo animado del Dr.Quantum - Experimento de doble rendija para obtener una descripción fácil de entender de la dualidad de onda-partícula y los experimentos asociados.
Ejemplo \(\PageIndex{1}\): Calculando la longitud de onda de una partícula
Si un electrón viaja a una velocidad de 1.000 × 107 m s–1 y tiene una masa de 9.109 × 10–28 g, cual es la longitud de la onda?
Solucion
Podemos usar la ecuación de De Broglie para resolver este problema, pero primero debemos hacer una conversión unitaria de el constante de Planck. Ya aprendió que 1 J = 1 kg m2/s2. Por lo tanto, podemos escribir h = 6.626 × 10–34 J s como 6.626 × 10–34 kg m2/s.
&=\mathrm{\dfrac{6.626×10^{−34}\:kg\: m^2/s}{(9.109×10^{−31}\:kg)(1.000×10^7\:m/s)}}\\
&=\mathrm{7.274×10^{−11}\:m}
\end{align*}\)
Este es un valor pequeño, pero es significativamente más grande que el tamaño de un electrón en la vista clásica (partícula). Este tamaño es del mismo orden de magnitud que el tamaño de un átomo. Esto significa que el comportamiento de una onda electrónica se notará en un átomo.
Ejercicio \(\PageIndex{1}\)
Calcule la longitud de onda de una pelota de softball con una masa de 100 g viajando a una velocidad de 35 ms-1, suponiendo que se puede modelar como una sola partícula.
- Respuesta
-
1.9 × 10–34 m.
Nunca pensamos que una pelota de softball lanzada tenga una longitud de onda, su longitud de onda es tan pequeña que es imposible que nuestros sentidos o cualquier instrumento conocido la detecte (hablando estrictamente, la longitud de la onda de una pelota de béisbol real correspondería a las longitudes de onda de sus átomos y moléculas constituyentes, que aunque es mucho más grande que este valor, aún sería microscópicamente pequeño). La longitud de la onda de De Broglie solo es apreciable para la materia que tiene una masa muy pequeña y/o una velocidad muy alta.
Werner Heisenberg consideró los límites de la precisión con la que podemos medir las propiedades de un electrón u otras partículas microscópicas. Determinó que existe un límite fundamental en que tan preciso se puede medir la posición de una partícula y su impulso simultáneamente. Cuanto más exactamente midamos el impulso de una partícula, menos podemos determinar su posición en ese momento y viceversa. Esto se resume en lo que ahora llamamos el principio de incertidumbre de Heisenberg: es fundamentalmente imposible determinar de manera simultánea y exacta tanto el momento como la posición de una partícula. Para una partícula de masa m que se mueve con la velocidad vx en la dirección x (o de manera equivalente con el impulso px), el producto de la incertidumbre en la posición, Δx, y la incertidumbre en el momento, Δpx, debe ser más grande o igual que \(\dfrac{ℏ}{2}\) (recuerde que \(ℏ=\dfrac{h}{2π}\), el valor de el constante de Planck dividido por 2π).
\[Δx×Δp_x=(Δx)(mΔv)≥\dfrac{ℏ}{2}\]
Esta ecuación nos permite calcular el límite de la precisión con la que podemos conocer la posición simultánea de un objeto y su momento. Por ejemplo, si mejoramos nuestra medición de la posición de un electrón para que la incertidumbre en la posición (Δx) tenga un valor de, por ejemplo, 1 pm (10-12 m, aproximadamente 1% del diámetro de un átomo de hidrógeno), entonces nuestra determinación de su impulso debe tener una incertidumbre con un valor de al menos
\[\left [Δp=mΔv=\dfrac{h}{(2Δx)} \right ]=\mathrm{\dfrac{(1.055×10^{−34}\:kg\: m^2/s)}{(2×1×10^{−12}\:m)}=5×10^{−23}\:kg\: m/s.}\]
El valor de ħ no es grande, por eso la incertidumbre en la posición o el impulso de un objeto macroscópico como una pelota de béisbol es demasiado insignificante para observar. Sin embargo, la masa de un objeto microscópico, como un electrón, es lo suficientemente pequeñoa como para que la incertidumbre sea grande y significativa.
Se debería notar que el principio de incertidumbre de Heisenberg no solo se limita a las incertidumbres en la posición y el impulso, sino que también vincula otras variables dinámicas. Por ejemplo, cuando un átomo absorbe un fotón y hace una transición de un estado de energía a otro, la incertidumbre en la energía y la incertidumbre en el tiempo requerido para la transición se relacionan de manera similar, como ΔE Δt ≥ \(\dfrac{ℏ}{2}\). Como veremos más adelante, incluso los componentes vectoriales del momento angular no se pueden especificar exactamente de manera simultánea.
El principio de Heisenberg impone límites definitivos a lo que se sabe en la ciencia. Se puede demostrar que el principio de incertidumbre es una consecuencia de la dualidad de onda-partícula, que se encuentra en el corazón de lo que distingue a la teoría cuántica moderna de la mecánica clásica. Recuerde que las ecuaciones de movimiento obtenidas de la mecánica clásica son trayectorias donde, en cualquier momento dado en el tiempo, tanto la posición como el impulso de una partícula se pueden determinar con exactitud. El principio de incertidumbre de Heisenberg implica que tal visión es insostenible en el dominio microscópico y que existen limitaciones fundamentales que dominan el movimiento de las partículas cuánticas. Esto no significa que las partículas microscópicas no se mueven en las trayectorias, solo significa que las mediciones de las trayectorias están limitadas en su precisión. En el ámbito de la mecánica cuántica, las mediciones introducen cambios en el sistema que se está observando.
El modelo cuántico-mecánico de un átomo
Poco después, de Broglie publicó sus ideas de que el electrón en un átomo de hidrógeno se podría considerar mejor como una onda estacionaria circular en lugar de una partícula que se mueve en órbitas circulares cuantificadas, como Bohr había argumentado. Erwin Schrödinger extendió el trabajo de Broglie incorporando la Relación de Broglie en una ecuación de onda, derivando lo que hoy se conoce como la ecuación de Schrödinger. Cuando Schrödinger aplicó su ecuación a átomos similares al hidrógeno, pudo reproducir la expresión de Bohr para la energía y, por lo tanto, la fórmula de Rydberg que gobierna los espectros de hidrógeno, y lo hizo sin tener que invocar las suposiciones de Bohr de estados estacionarios y órbitas cuantificadas, momento angular, y energías; la cuantificación en la teoría de Schrödinger fue una consecuencia natural de las matemáticas subyacentes de la ecuación de la onda. Similar a de Broglie, Schrödinger inicialmente vio el electrón en el hidrógeno como una onda física en lugar de una partícula, pero cuando De Broglie pensó en el electrón en términos de ondas estacionarias circulares, Schrödinger pensó correctamente en términos de ondas estacionarias tridimensionales, o funciones de la onda representado por la letra griega psi ψ. Unos años más tarde, Max Born propuso una interpretación de la función de onda que todavía se acepta: los electrones son todavía partículas, las ondas representadas por ψ no son ondas físicas, sino que, en cambio, son amplitudes de probabilidad complejas. El cuadrado de la magnitud de una función de onda \(∣ψ∣^2\) describe la probabilidad de que la partícula cuántica esté presente cerca de cierta ubicación en el espacio. Esto significa que las funciones de onda se pueden usar para determinar la distribución de la densidad del electrón con respecto al núcleo en un átomo. En la forma más general, la ecuación de Schrödinger se puede escribir como:
\[\hat{H}ψ=Eψ\]
\(\hat{H}\) es el operador hamiltoniano, un conjunto de operaciones matemáticas que representan la energía total de la partícula cuántica (como un electrón en un átomo), ψ es la función de la onda de esta partícula que se puede usar para encontrar la distribución especial de la probabilidad de encontrar la partícula, y \(E\) es el valor real de la energía total de la partícula. El trabajo de Schrödinger, así como el de Heisenberg y muchos otros científicos que siguen sus pasos, generalmente se conoce como la mecánica cuántica.
Es posible que también hayas escuchado de Schrödinger por su famoso experimento mental. Esta historia explica los conceptos de superposición y enredo relacionados con un gato en una caja con veneno (https://www.youtube.com/watch?v=IOYy...eature=youtube).
Comprensión de la teoría cuántica de los electrones en los átomos
El objetivo de esta sección es comprender los orbitales electrónicos (ubicación de los electrones en los átomos), sus diferentes energías y otras propiedades. El uso de la teoría cuántica nos da la mejor comprensión de estos temas. Este conocimiento es un precursor del enlace químico.
Como se describió anteriormente, los electrones en los átomos pueden existir solo en niveles de energía discretos pero no entre los niveles de energía. Se dice que la energía de un electrón en un átomo se cuantifica, es decir, puede ser igual solo a ciertos valores específicos y puede saltar de un nivel de energía a otro pero no hacer una transición suave o permanecer entre estos niveles.
Los niveles de energía están etiquetados con un valor n, donde n=1,2,3,…. En términos generales, la energía de un electrón en un átomo es más grande para valores mayores de n. Este número, n, se conoce como el número cuántico principal. El número cuántico principal define la ubicación del nivel de energía. Es esencialmente el mismo concepto que el n en la descripción del átomo de Bohr. Otro nombre para el número cuántico principal es el número de capa. Se puede pensar en las conchas de un átomo en círculos concéntricos que irradian desde el núcleo. Los electrones que pertenecen a una capa específica tienen mayor probabilidad de encontrarse dentro del área circular correspondiente. Cuanto más nos alejemos del núcleo,el número de capa será más grande y, por lo tanto, mayor será el nivel de energía (Figura \(\PageIndex{5}\)). Los protones cargados positivamente en el núcleo estabilizan los orbitales electrónicos por atracción electrostática entre las cargas positivas de los protones y las cargas negativas de los electrones. Así, cuanto más lejos esté el electrón del núcleo, mayor será la energía que tiene.
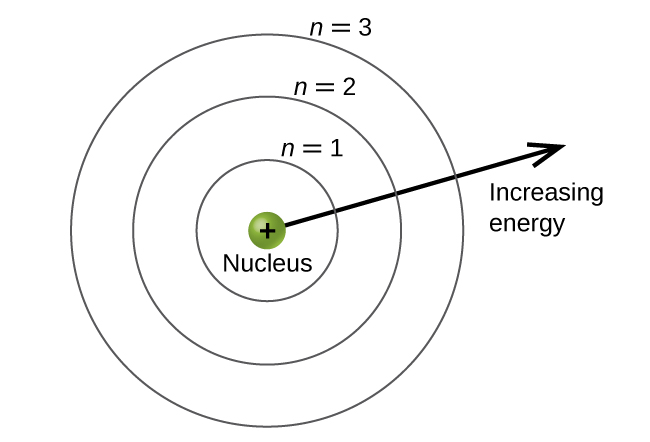
Este modelo mecánico cuántico para el lugar donde están los electrones en un átomo se puede usar para observar las transiciones electrónicas, los eventos en que un electrón se mueve de un nivel de energía a otro. Si la transición es a un nivel de energía más alto, la energía se absorbe y el cambio de energía tiene un valor positivo. Para obtener la cantidad de energía necesaria para la transición a un nivel de energía más alto, el fotón es absorbido por el átomo. Una transición a un nivel de energía más bajo implica una liberación de energía, y el cambio de energía es negativo. Este proceso es acompañado por la emisión de un fotón por el átomo. La siguiente ecuación resume estas relaciones y se basa en el átomo de hidrógeno:
\[ \begin{align*} ΔE &=E_\ce{final}−E_\ce{initial} \\[5pt] &=−2.18×10^{−18}\left(\dfrac{1}{n^2_\ce f}−\dfrac{1}{n^2_\ce i}\right)\:\ce J \end{align*} \]
Los valores nf y ni son los estados energéticos finales e iniciales del electrón.
El número cuántico principal es uno de los tres números cuánticos usados para caracterizar un orbital. Un orbital atómico, que es distinto de una órbita, es una región general en un átomo dentro del cual es más probable que este un electrón. El modelo mecánico cuántico especifica la probabilidad de encontrar un electrón en el espacio tridimensional alrededor del núcleo y se basa en soluciones de la ecuación de Schrödinger. Además, el número cuántico principal define la energía de un electrón en un hidrógeno o un átomo similar a hidrógeno o un ion (un átomo o un ion con un solo electrón) y la región general en la que los niveles discretos de la energía de los electrones en átomos de varios electrones y los iones están localizados.
Otro número cuántico es l, el número cuántico de momento angular. Es un número entero que define la forma del orbital y toma los valores, l = 0,1,2,…, n - 1. Esto significa que un orbital con n =1 puede tener solo un valor de l, l = 0, mientras que n = 2 permite l = 0 y l = 1, y así sucesivamente. El número cuántico principal define el tamaño general y la energía del orbital. El valor de l especifica la forma del orbital. Los orbitales con el mismo valor de l forman una subcapa. Además, cuanto mayor es el número cuántico de momento angular, mayor es el momento angular de un electrón en este orbital.
Los orbitales con l = 0 se llaman orbitales s (o las subcapas s). El valor l = 1 corresponde a los orbitales p. Para un n dado, los orbitales p constituyen una subcapa p (por ejemplo, 3p si n = 3). Los orbitales con l = 2 se llaman orbitales d, seguidos de los orbitales f, g y h para l = 3, 4, 5, y hay valores más altos que no consideraremos.
Hay ciertas distancias desde el núcleo a las cuales la densidad de probabilidad de encontrar un electrón ubicado en un orbital particular es cero. En otras palabras, el valor de la función de la onda ψ es cero a esta distancia para este orbital. Dicho valor de radio r se llama el nodo radial. El número de nodos radiales en un orbital es n - l - 1.
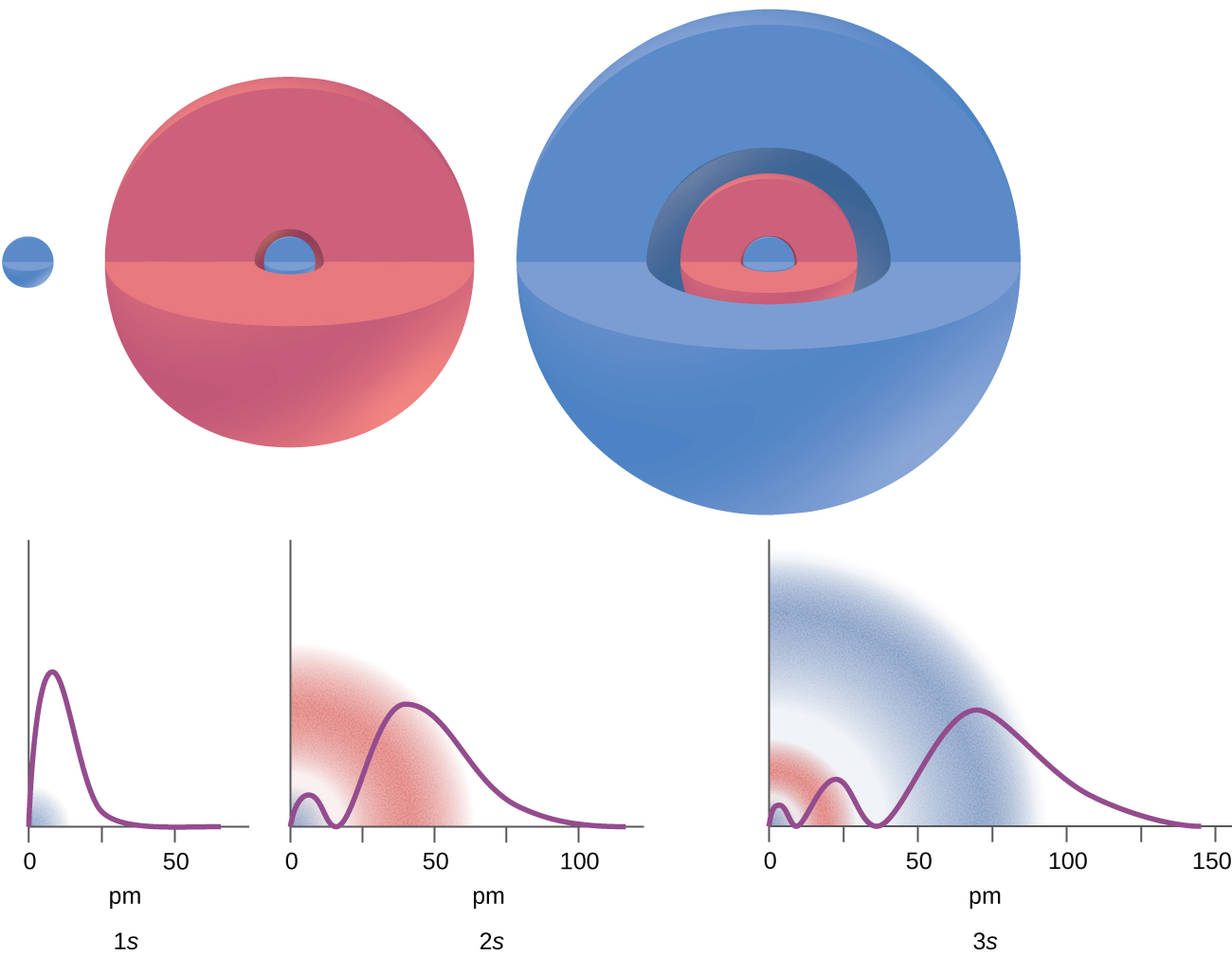
Considere los ejemplos en la Figura \(\PageIndex{7}\). Los orbitales representados son del tipo s, por lo tanto, l = 0 para todos ellos. En las gráficas de las densidades de probabilidad se puede ver que hay 1 - 0 - 1 = 0 lugares donde la densidad es cero (nodos) para 1s (n = 1), 2 - 0 - 1 = 1 nodo para 2s, y 3 - 0 - 1 = 2 nodos para los orbitales 3s.
La distribución de la densidad de los electrones de la subcapa es esférica y la subcapa p tiene una forma de mancuerna. Los orbitales d y f son más complejos. Estas formas representan las regiones tridimensionales dentro de las cuales es probable que se encuentre el electrón.
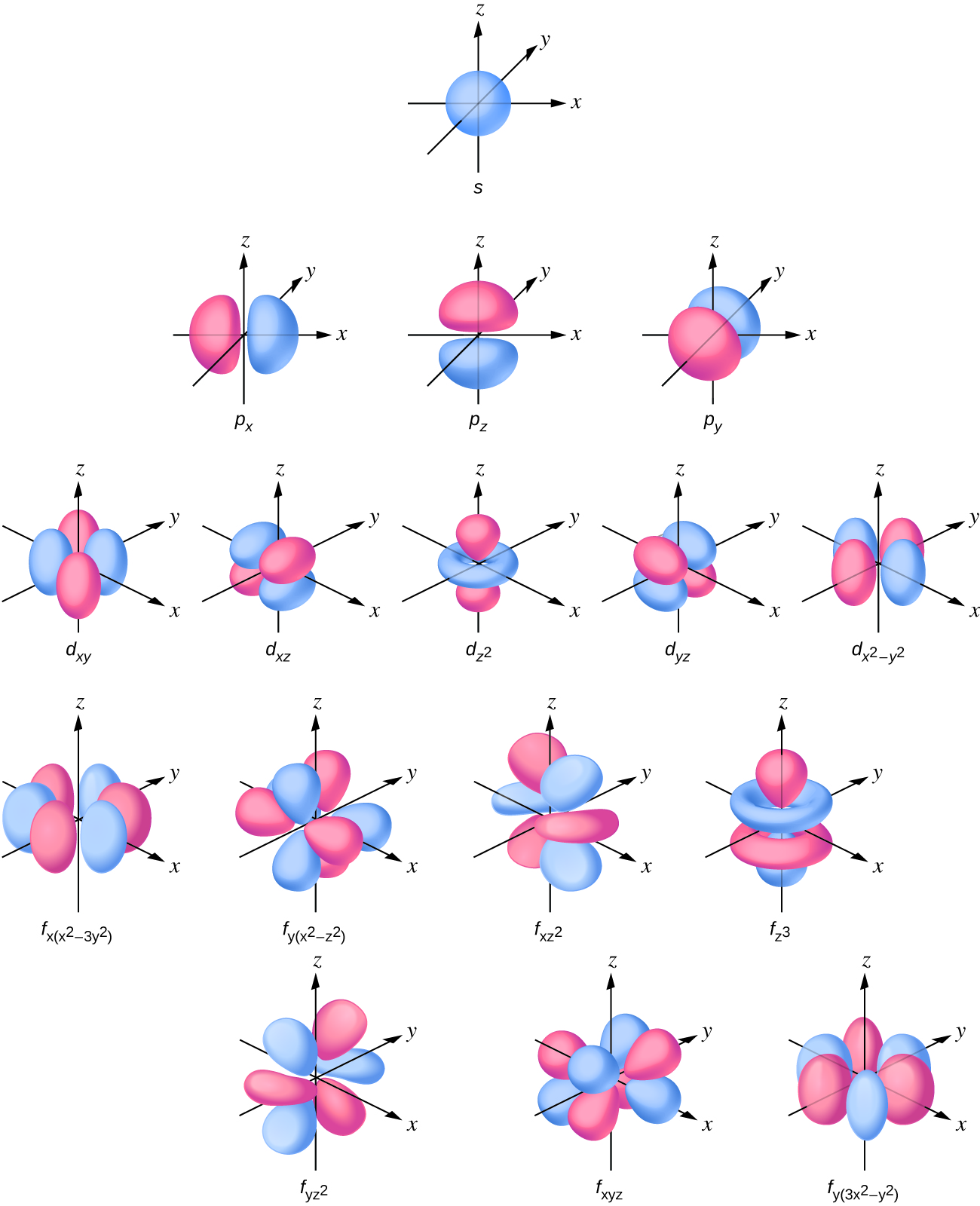
Si un electrón tiene un momento angular (l ≠ 0), entonces este vector puede puntar en diferentes direcciones. Además, el componente z del momento angular puede tener más de un valor. Esto significa que, si se aplica un campo magnético en la dirección z, los orbitales con diferentes valores de el componente z del momento angular tendrán diferentes energías resultantes de la interacción con el campo. El número cuántico magnético, llamado ml, especifica el componente z del momento angular para un orbital en particular. Por ejemplo, para un orbital s, l = 0, y el único valor de ml es cero. Para p orbitales, l = 1, y ml puede ser igual a –1, 0 o +1. En términos generales, ml puede ser igual a –l, - (l - 1),…, –1, 0, +1,…, (l - 1), l. El número total de orbitales posibles con el mismo valor de l (una subcapa) es 2l + 1. Por lo tanto, hay un s-orbital para ml= 0, hay tres p-orbital para ml = 1, cinco d-orbital para ml= 2, siete orbitales-f para ml= 3, y así sucesivamente. El número cuántico principal define el valor general de la energía electrónica. El número cuántico de momento angular determina la forma del orbital. Y el número cuántico magnético especifica la orientación del orbital en el espacio, como se puede ver en la Figura \(\PageIndex{7}\).
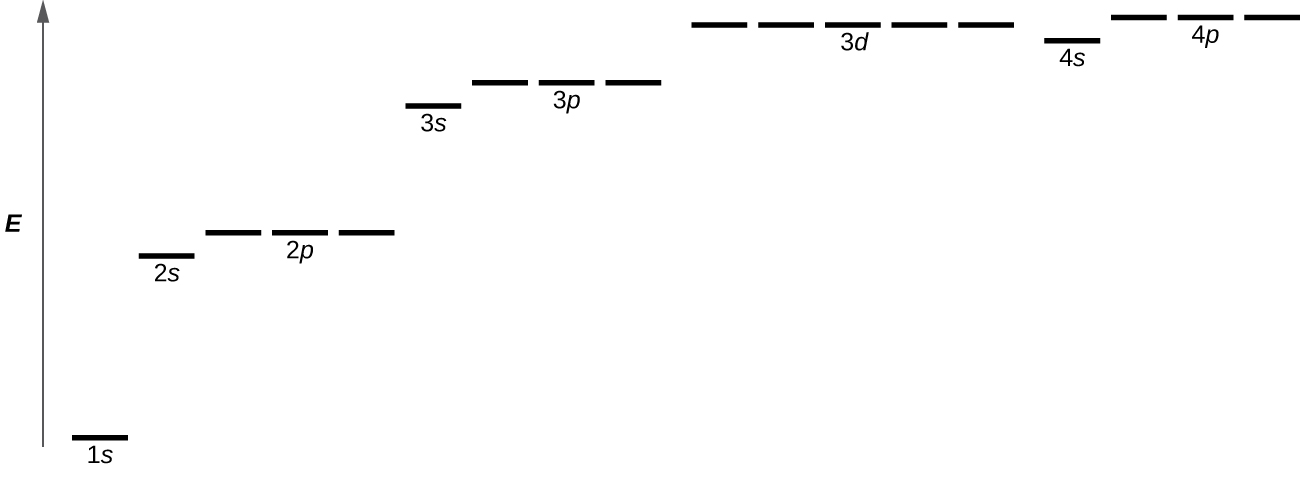
Figura \(\PageIndex{8}\) Ilustra los niveles de energía para varios orbitales. El número antes del nombre orbital (como 2s, 3p, etc.) representa el número cuántico principal, n. La letra en el nombre orbital define la subcapa con un número cuántico de momento angular específico l = 0 para orbitales s, 1 para p orbitales, 2 para d orbitales. Finalmente, hay más de un orbital posible para l ≥ 1, cada uno correspondiente a un valor específico de ml. En el caso de un átomo de hidrógeno o un ion de un electrón (como He+, Li2+, etc.), las energías de todos los orbitales con la misma n son iguales. Esto se llama degeneración, y los niveles de energía para el mismo número cuántico principal, n, se llaman niveles de energía degenerados. Sin embargo, en los átomos con más de un electrón, esta degeneración se elimina por las interacciones de electrón-electrón, y los orbitales que pertenecen a diferentes subcapas tienen diferentes energías. Los orbitales dentro del la misma subcapa (por ejemplo, ns, np, nd, nf, como 2p, 3s) todavía están degenerados y tienen la misma energía.
Mientras los tres números cuánticos analizados en los párrafos anteriores funcionan bien para describir orbitales de electrones, algunos experimentos demostraron que no eran suficientes para explicar todos los resultados observados. Se demostró en la década de 1920 que cuando los espectros de líneas de hidrógeno se examinan con una resolución extremadamente alta, algunas líneas no son en realidad picos individuales sino pares de líneas muy espaciadas. Esto pasa por la estructura fina del espectro, e implica que existen pequeñas diferencias adicionales en las energías de los electrones, incluso cuando se encuentran en el mismo orbital. Estas observaciones llevaron a Samuel Goudsmit y George Uhlenbeck a proponer que los electrones tienen un cuarto número cuántico. Llamaron a esto el número cuántico de espín, o ms.
Los otros tres números cuánticos, n, l y ml., son propiedades de orbitales atómicos específicos que también definen en qué parte del espacio es más probable que se ubique un electrón. Los orbitales son el resultado de resolver la ecuación de Schrödinger para los electrones en los átomos. El giro electrónico es un diferente tipo de propiedad. Es un fenómeno completamente cuántico sin análogos en el reino clásico. Además, no se puede derivar de resolver la ecuación de Schrödinger y no está relacionado con las coordenadas espaciales normales (como la cartesiana x, y, y z). El giro del electrón describe una "rotación" o "giro" intrínseco del electrón. Cada electrón actúa como un imán pequeño o un objeto giratorio pequeño con un momento angular, aunque esta rotación no se puede observar en términos de las coordenadas espaciales.
La magnitud del espín general de electrones solo puede tener un valor, y un electrón solo puede "girar" en uno de los dos estados cuantificados. Uno se llama el estado α, y el componente z del giro se encuentra en la dirección positiva del eje z. Esto corresponde al número cuántico de espín \(m_s=\dfrac{1}{2}\). El otro se llama el estado β, con el componente z del giro negativo y \(m_s=-\dfrac{1}{2}\). Cualquier electrón, independientemente del orbital atómico en el que se encuentre, solo puede tener uno de esos dos valores del número cuántico de espín. Las energías de los electrones que tienen \(m_s=-\dfrac{1}{2}\) y \(m_s=\dfrac{1}{2}\) son diferentes si se aplica un campo magnético externo.
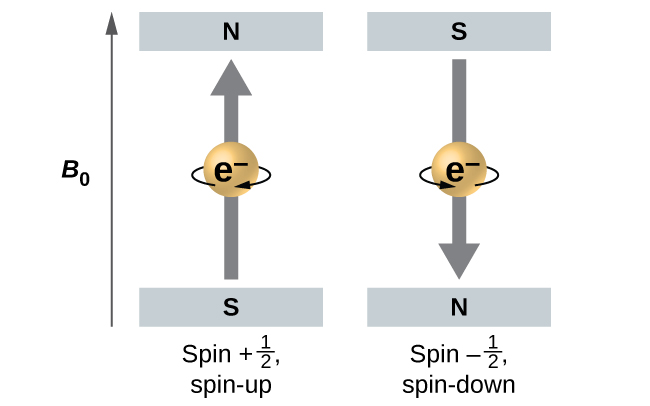
Figura \(\PageIndex{9}\) ilustra este fenómeno. Un electrón actúa como un pequeño imán. Su momento se dirige hacia arriba (en la dirección positiva del eje z) para el \(\dfrac{1}{2}\) número cuántico de giro y hacia abajo (en la dirección z negativa) para el número cuántico de giro de \(-\ce{1/2}\). Un imán tiene una energía más baja si su momento magnético está alineado con el campo magnético externo (el electrón izquierdo) y una energía más alta para el momento magnético es opuesta al campo aplicado. Esta es la razón por la que un electrón con \(m_s=\dfrac{1}{2}\) tiene una energía un poco menos que en un campo externo en la dirección z positiva, y un electrón con \(m_s=-\dfrac{1}{ 2}\) tiene una energía un poco más grande en el mismo campo. Esto es cierto incluso para un electrón que ocupa el mismo orbital en un átomo. Una línea espectral correspondiente a una transición para electrones del mismo orbital, pero con diferentes números cuánticos de espín tiene dos valores posibles de energía; por lo tanto, la línea en el espectro mostrará una estructura fina dividida.
El principio de exclusión de Pauli
Un electrón en un átomo se describe completamente mediante cuatro números cuánticos: n, l, ml y ms. Los tres primeros números cuánticos definen el orbital y el cuarto número cuántico describe la propiedad electrónica intrínseca llamada el espín. Un físico austriaco Wolfgang Pauli formuló un principio general que nos da la última información que necesitamos para comprender el comportamiento general de los electrones en los átomos. El principio de exclusión de Pauli se puede formular de la siguiente manera: no hay dos electrones en el mismo átomo que puedan tener exactamente el mismo conjunto de los cuatro números cuánticos. Lo que esto significa es que los electrones pueden compartir el mismo orbital (el mismo conjunto de los números cuánticos n, l y ml ), pero solo si sus números cuánticos de espín tienen valores diferentes. Dado que el número cuántico de espín solo puede tener dos valores \(\left(±\dfrac{1}{2}\right)\), no más de dos electrones pueden ocupar el mismo orbital (y si dos electrones están ubicados en el mismo orbital, deben tener giros opuestos). Por lo tanto, cualquier orbital atómico puede ser poblado por solo cero, uno o dos electrones. Las propiedades y el significado de los números cuánticos de electrones en los átomos se resumen brevemente en la Tabla \(\PageIndex{1}\).
| Nombre | Símbolo | Valores Permitidos | Significado físico |
|---|---|---|---|
| número cuántico principal | n | 1, 2, 3, 4, …. |
capa, la región general para el valor de la energía de un electrón en el orbital |
| El momento angular o el número cuántico azimutal | l | 0 ≤ l ≤ n – 1 | subcapa, la forma del orbital |
| el número cuántico magnético | ml | – l ≤ ml ≤ l | orientación del orbital |
| el número cuántico de espín | ms | \(\dfrac{1}{2},\:−\dfrac{1}{2}\) | dirección del "giro" cuántico intrínseco del electrón |
Ejemplo \(\PageIndex{2}\): TRABAJANDO CON capas Y SUBcapas
Indique el número de subcapas, el número de orbitales en cada subcapa y los valores de 1 y ml para los orbitales en la capa n = 4 de un átomo.
Solución
Para n = 4, l puede tener valores de 0, 1, 2 y 3. Por lo tanto, las subcapas s, p, d y f se encuentran en la capa n = 4 de un átomo. Para l = 0 (la subcapa s), ml solo puede ser 0. Por lo tanto, solo hay un orbital de 4s. Para l = 1 (orbitales tipo p), m puede tener valores de –1, 0, +1, por lo que encontramos tres orbitales 4p. Para l = 2 (orbitales tipo d), ml puede tener valores de –2, –1, 0, +1, +2, por lo que tenemos cinco orbitales 4d. Cuando l = 3 (orbitales tipo f), ml puede tener valores de –3, –2, –1, 0, +1, +2, +3, y podemos tener siete orbitales 4f. Por lo tanto, encontramos un total de 16 orbitales en la capa n = 4 de un átomo.
Ejercicio \(\PageIndex{2}\)
Identifique las subcapas en donde electrones con los siguientes números cuánticos se pueden encontrar:
- n = 3, l = 1;
- n = 5, l = 3;
- n = 2, l = 0.
- Respuesta a
-
3p
- Respuesta b
-
5f
- Respuesta c
-
2s
Ejemplo \(\PageIndex{3}\): El numero máximo de electrones
Calcule el número máximo de electrones que pueden ocupar una capa con (a) n = 2, (b) n = 5 y (c) n como una variable. Tenga en cuenta que solo está mirando los orbitales con el valor n especificado, no aquellos con energías más bajas.
Solución
(a) Cuando n = 2, hay cuatro orbitales (un solo orbital 2s, y tres orbitales etiquetados como 2p). Estos cuatro orbitales pueden contener ocho electrones.
(b) Cuando n = 5, Hay cinco subcapas de orbitales que necesitamos sumar:
&\phantom{+}\textrm{1 orbital labeled }5s\\
&\phantom{+}\textrm{3 orbitals labeled }5p\\
&\phantom{+}\textrm{5 orbitals labeled }5d\\
&\phantom{+}\textrm{7 orbitals labeled }5f\\
&\underline{+\textrm{9 orbitals labeled }5g}\\
&\,\textrm{25 orbitals total}
\end{align*}\)
Una vez más, cada orbital tiene dos electrones, por lo que 50 electrones pueden caber en esta capa.
(c) El número de orbitales en cualquier capa n será igual a n2. Puede haber hasta dos electrones en cada orbital, por lo que el número máximo de electrones será 2 × n2
Ejercicio \(\PageIndex{3}\)
Si una capa contiene un máximo de 32 electrones, ¿Cuál es el número cuántico principal, n?
- Respuesta
-
n = 4
Ejemplo \(\PageIndex{4}\): TRABAJANDO CON NÚMEROS Cuánticos
Complete la siguiente tabla para los orbitales atómicos:
| Orbital | n | l | ml degeneración | Nodos radiales (no.) |
|---|---|---|---|---|
| 4f | ||||
| 4 | 1 | |||
| 7 | 7 | 3 | ||
| 5d |
Solución
La tabla se puede completar usando las siguientes reglas:
- La designación orbital es nl, donde l = 0, 1, 2, 3, 4, 5, ... se asigna a la secuencia de letras s, p, d, f, g, h, ...,
- La degeneración de ml es el número de orbitales dentro de una capa, y también es 2l + 1 (hay un orbital s, tres orbitales p, cinco orbitales d, siete orbitales f, etc.).
- El número de nodos radiales es igual a n - l - 1.
| Orbital | n | l | ml degeneración | Nodos radiales (no.) |
|---|---|---|---|---|
| 4f | 4 | 3 | 7 | 0 |
| 4p | 4 | 1 | 3 | 2 |
| 7f | 7 | 3 | 7 | 3 |
| 5d | 5 | 2 | 5 | 2 |
Ejercicio \(\PageIndex{4}\)
¿Cuantos orbitales tienen l = 2 y n = 3?
- Respuesta
-
Los cinco degenerados 3d orbitales
Resumen
Los objetos macroscópicos actúan como partículas. Los objetos microscópicos (como los electrones) tienen propiedades tanto de una partícula como de una onda. Sus trayectorias exactas no se pueden determinar. El modelo mecánico cuántico de los átomos describe la posición tridimensional del electrón de manera probabilística de acuerdo con una función matemática llamada la función de la onda, a menudo denotada como ψ. Las funciones de onda atómica también se llaman orbitales. La magnitud cuadrada de la función de onda describe la distribución de la probabilidad de encontrar el electrón en una región particular en el espacio. Por lo tanto, los orbitales atómicos describen las áreas en un átomo donde es más probable encontrar electrones.
Un orbital atómico se caracteriza por tres números cuánticos. El número cuántico principal, n, puede ser cualquier número entero positivo. La región general para el valor de la energía del orbital y la distancia promedio de un electrón desde el núcleo están relacionadas con n. Se dice que los orbitales que tienen el mismo valor de n están en la misma capa. El número cuántico de momento angular, l, puede tener cualquier valor entero de 0 a n - 1. Este número cuántico describe la forma o el tipo del orbital. Los orbitales con el mismo número cuántico principal y el mismo valor l pertenecen a la misma capa. El número cuántico magnético, ml, con valores de 2l + 1 que van de –l a + l, describe la orientación del orbital en el espacio. Además, cada electrón tiene un número cuántico de espín, ms, que puede ser igual a \(±\dfrac{1}{2}\). No hay dos electrones en el mismo átomo que puedan tener el mismo conjunto de valores para los cuatro números cuánticos.
Glosario
- número cuántico de momento angular (l)
- Número cuántico que distingue las diferentes formas de los orbitales; también es una medida del momento angular orbital.
- orbital atómico
- Función matemática que describe el comportamiento de un electrón en un átomo (también llamada función de onda), se puede usar para encontrar la probabilidad de ubicar un electrón en una región específica alrededor del núcleo, así como otras variables dinámicas.
- orbital d
- Región del espacio con alta densidad de electrones que tiene cuatro lóbulos o contiene una forma de mancuerna y toro; describe orbitales con l = 2. Un electrón en este orbital se llama un electrón d.
- densidad de electrones
- Una medida de la probabilidad de ubicar un electrón en una región particular del espacio, es igual al valor absoluto cuadrado de la función de onda ψ.
- orbital f
- La región multilobular del espacio con alta densidad de electrones, describe orbitales con l = 3. Un electrón en este orbital se llama un electrón f.
- Principio de incertidumbre de Heisenberg
- Regla que indica que es imposible determinar exactamente ciertas propiedades dinámicas conjugadas, como el impulso y la posición de una partícula al mismo tiempo. El principio de incertidumbre es una consecuencia de las partículas cuánticas que muestran una dualidad de la onda-partícula.
- número cuántico magnético (ml)
- Número cuántico que nos da la orientación de un orbital atómico alrededor del núcleo; los orbitales que tienen diferentes valores de ml, pero el mismo valor de capa de l tienen la misma energía (son degenerados), pero esta degeneración se puede eliminar mediante la aplicación de un campo magnético externo.
- orbital p
- Región del espacio con forma de mancuerna con alta densidad de electrones, describe orbitales con l = 1. Un electrón en este orbital se llama un electrón p.
- principio de exclusión de Pauli
- Especifica que no hay dos electrones en un átomo que puedan tener el mismo valor para los cuatro números cuánticos.
- número cuántico principal (n)
- Número cuántico que especifica la capa que un electrón ocupa en un átomo.
- la mecánica cuántica
- El campo de estudio que incluye la cuantificación de la energía, la dualidad de la onda-partícula y el principio de incertidumbre de Heisenberg para describir la materia.
- orbital s
- La región esférica del espacio con alta densidad electrónica, describe orbitales con l = 0. Un electrón en este orbital se llama un electrón s.
- capa
- Un conjunto de orbitales con el mismo número cuántico principal, n.
- número cuántico de espín (ms)
- Número que especifica la dirección de giro del electrón, ya sea \(+\dfrac{1}{2}\) o \(−\dfrac{1}{2}\).
- subcapa
- Conjunto de orbitales en un átomo con los mismos valores de n y l.
- función de onda (ψ)
- La descripción matemática de un orbital atómico que describe la forma del orbital; se puede usar para calcular la probabilidad de encontrar el electrón en cualquier ubicación dada en el orbital, así como variables dinámicas como la energía y el momento angular.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


