7.5: Fortaleza de los enlaces iónicos y covalentes

habilidades para desarrollar

• Describir la energía de la formación y ruptura de enlaces iónicos y covalentes.
• Utilizar el ciclo de Born-Haber para calcular las energías reticulares de los compuestos iónicos.
• Usar energías de enlace covalente promedio para estimar entalpías de reacción

La fuerza de un enlace describe la fuerza con la que cada átomo se une a otro átomo y, por lo tanto, cuánta energía se requiere para romper el enlace entre los dos átomos. En esta sección, aprenderá sobre la fuerza de los enlaces covalentes, y luego la comparará con la fuerza de los enlaces iónicos, que está relacionada con la energía reticular de un compuesto.

La fuerza de enlace: enlaces covalentes

Moléculas estables existen porque los enlaces covalentes mantienen unidos a los átomos. Medimos la fuerza de un enlace covalente por la energía requerida para romperlo, es decir, la energía necesaria para separar los átomos unidos. Separar cualquier par de átomos unidos requiere energía; cuanto más fuerte es un enlace, mayor es la energía requerida para romperlo. La energía requerida para romper un enlace covalente específico en un mol de moléculas gaseosas se llama la energía de enlace o energía de disociación de enlace. La energía de enlace para una molécula diatómica, \(D_{X–Y}\), se define como el cambio de entalpía estándar para la reacción endotérmica:

\[XY_{(g)}⟶X_{(g)}+Y_{(g)}\;\;\; D_{X−Y}=ΔH° \label{7.6.1}\]

Por ejemplo, la energía del enlace covalente puro de H – H, \(\Delta_{H–H}\), es 436 kJ por mol de enlaces H – H separados.

\[H_{2(g)}⟶2H_{(g)} \;\;\; D_{H−H}=ΔH°=436kJ \label{EQ2}\]

Romper un enlace siempre requiere que se agregue energía a la molécula. En consecuencia, formar un enlace siempre libera energía.

Las moléculas con tres o más átomos tienen dos o más enlaces. La suma de todas las energías de enlace en dicha molécula es igual al cambio de entalpía estándar para la reacción endotérmica que rompe todos los enlaces en la molécula. Por ejemplo, la suma de las cuatro energías de enlace C – H en CH₄, 1660 kJ, es igual al cambio de entalpía estándar de la reacción:

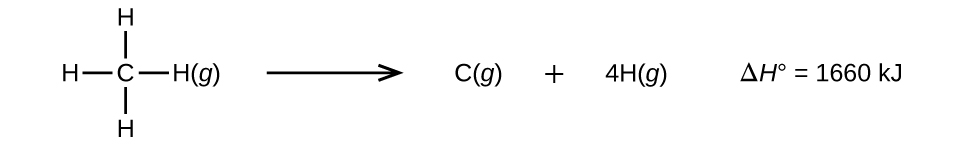
La energía promedio del enlace C–H, \(D_{C–H}\), es 1660/4 = 415 kJ/mol porque hay cuatro moles de enlaces C–H separados por mol de la reacción. Aunque los cuatro enlaces de C–H son equivalentes en la molécula original, no requieren la misma energía para romperse; una vez que se rompe el primer enlace (que requiere 439 kJ/mol), los enlaces restantes son más fáciles de romper. El valor de 415 kJ/mol es el promedio, no el valor exacto requerido para romper cualquier enlace.

La fuerza de un enlace entre dos átomos aumenta a medida que aumenta el número de pares de electrones en el enlace. Generalmente, a medida que aumenta la resistencia de la unión, la longitud de la unión disminuye. Por lo tanto, encontramos que los enlaces triples son más fuertes y cortos que los enlaces dobles entre los mismos dos átomos; asimismo, los enlaces dobles son más fuertes y más cortos que los enlaces simples entre los mismos dos átomos. Las energías de enlace promedio para algunos enlaces comunes aparecen en la Tabla \(\PageIndex{2}\), y una comparación de las longitudes de enlace y las fuerzas de enlace para algunos enlaces comunes aparece en la Tabla \(\PageIndex{2}\). Cuando un átomo se une a varios átomos en un grupo, la fuerza del enlace generalmente disminuye a medida que avanzamos hacia abajo del grupo. Por ejemplo, C–F es 439 kJ/mol, C–Cl es 330 kJ/mol y C–Br es 275 kJ/mol.

Tabla \(\PageIndex{1}\): Energías de enlace (kJ/mol)

Enlace	Energías de enlace		Enlace	Energías de enlace		Enlace	Energías de enlace
H–H	436		C–S	260		F–Cl	255
H–C	415		C–Cl	330		F–Br	235
H–N	390		C–Br	275		Si–Si	230
H–O	464		C–I	240		Si–P	215
H–F	569		N–N	160		Si–S	225
H–Si	395		\(\mathrm{N=N}\)	418		Si–Cl	359
H–P	320		\(\mathrm{N≡N}\)	946		Si–Br	290
H–S	340		N–O	200		Si–I	215
H–Cl	432		N–F	270		P–P	215
H–Br	370		N–P	210		P–S	230
H–I	295		N–Cl	200		P–Cl	330
C–C	345		N–Br	245		P–Br	270
\(\mathrm{C=C}\)	611		O–O	140		P–I	215
\(\mathrm{C≡C}\)	837		\(\mathrm{O=O}\)	498		S–S	215
C–N	290		O–F	160		S–Cl	250
\(\mathrm{C=N}\)	615		O–Si	370		S–Br	215
\(\mathrm{C≡N}\)	891		O–P	350		Cl–Cl	243
C–O	350		O–Cl	205		Cl–Br	220
\(\mathrm{C=O}\)	741		O–I	200		Cl–I	210
\(\mathrm{C≡O}\)	1080		F–F	160		Br–Br	190
C–F	439		F–Si	540		Br–I	180
C–Si	360		F–P	489		I–I	150
C–P	265		F–S	285

Tabla \(\PageIndex{2}\): Promedio de longitudes de enlace y energías de enlace para algunos enlaces comunes

Enlace	Longitud de Enlace (Å)	Energía de Enlace (kJ/mol)
C–C	1.54	345
\(\mathrm{C=C}\)	1.34	611
\(\mathrm{C≡C}\)	1.20	837
C–N	1.43	290
\(\mathrm{C=N}\)	1.38	615
\(\mathrm{C≡N}\)	1.16	891
C–O	1.43	350
\(\mathrm{C=O}\)	1.23	741
\(\mathrm{C≡O}\)	1.13	1080

Podemos usar energías de enlace para calcular los cambios aproximados de entalpía para reacciones en las que las entalpías de formación no están disponibles. Los cálculos de este tipo también nos dirán si una reacción es exotérmica o endotérmica.

• Se produce una reacción exotérmica (ΔH negativa, producida por calor) cuando los enlaces en los productos son más fuertes que los enlaces en los reactivos.
• Se produce una reacción endotérmica (ΔH positiva, absorbida por calor) cuando los enlaces en los productos son más débiles que los de los reactivos.

El cambio de entalpía, ΔH, para una reacción química es aproximadamente igual a la suma de la energía requerida para romper todos los enlaces en los reactivos (energía "entrando", signo positivo) más la energía liberada cuando se forman todos los enlaces en los productos (energía "suelta", signo negativo). Esto se puede expresar matemáticamente de la siguiente manera:

\[\Delta H=\sum D_{\text{bonds broken}}− \sum D_{\text{bonds formed}} \label{EQ3}\]

En esta expresión, el símbolo \(\Sigma\) significa "la suma de" y D representa la energía de enlace en kilojulios por mol, que siempre es un número positivo. La energía del enlace se obtiene de una tabla y dependerá de si el enlace particular es un enlace simple, doble o triple. Por lo tanto, al calcular las entalpías de esta manera, es importante que consideremos los enlaces en todos los reactivos y productos. Debido a que los valores D suelen ser promedios para un tipo de enlace en muchas moléculas diferentes, este cálculo nos da una estimación aproximada, no un valor exacto, para la entalpía de la reacción.

Considere la siguiente reacción:

\[\ce{H_{2(g)} + Cl_{2(g)}⟶2HCl_{(g)}} \label{EQ4}\]

o

\[\ce{H–H_{(g)} + Cl–Cl_{(g)}⟶2H–Cl_{(g)}} \label{\EQ5}\]

Para formar dos moles de HCl, se deben romper un mol de enlaces H – H y un mol de enlaces Cl – Cl. La energía requerida para romper estos enlaces es la suma de la energía de enlace, del enlace H – H (436 kJ/mol) y el enlace Cl – Cl (243 kJ/mol). Durante la reacción, se forman dos moles de enlaces H – Cl (energía de enlace = 432 kJ/mol), liberando 2 × 432 kJ; o 864 kJ. Debido a que los enlaces en los productos son más fuertes que los de los reactivos, la reacción libera más energía que absorbe:

\[\begin {align*}
ΔH&= \sum \mathrm{D_{bonds\: broken}}− \sum \mathrm{D_{bonds\: formed}}\\
ΔH&=\mathrm{[D_{H−H}+D_{Cl−Cl}]−2D_{H−Cl}}\\
&=\mathrm{[436+243]−2(432)=−185\:kJ}
\end {align*}\]

Este exceso de energía se libera como calor, por lo que la reacción es exotérmica. Tabla T2 nos da un valor para la entalpía molar estándar de la formación de HCl(g), \(ΔH^\circ_\ce f\), de –92.307 kJ/mol. Dos veces ese valor es –184.6 kJ, lo que concuerda bien con la respuesta obtenida anteriormente para la formación de dos moles de HCl.

Ejemplo \(\PageIndex{1}\): Uso de energías de enlace para aproximar los cambios de entalpía

El metanol, CH₃OH, puede ser un excelente combustible alternativo. La reacción a alta temperatura de vapor y carbono produce una mezcla de los gases monóxido de carbono, CO e hidrógeno, H₂, a partir de los cuales se puede producir el metanol. Usando las energías de enlace en la Tabla \(\PageIndex{2}\), calcule el cambio aproximado de entalpía, ΔH, para la reacción aquí:

\[CO_{(g)}+2H2_{(g)}⟶CH_3OH_{(g)}\]

Solución

Primero, necesitamos que escribir las estructuras de Lewis de los reactivos y los productos:

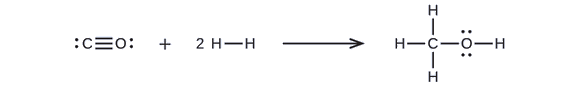
A partir de esto, vemos que ΔH para esta reacción involucra la energía requerida para romper un triple enlace C – O y dos enlaces simples H – H, así como la energía producida por la formación de tres enlaces simples C – H, un C– O enlace sencillo y un enlace sencillo de O-H. Podemos expresar esto de la siguiente manera (a través de la ecuación \ref{EQ3}):

\[\begin {align*}
ΔH&= \sum D_{bonds\: broken}− \sum D_{bonds\: formed}\\
ΔH&=\mathrm{[D_{C≡O}+2(D_{H−H})]−[3(D_{C−H})+D_{C−O}+D_{O−H}]}
\end {align*}\]

Usando los valores de energía de enlace en la Tabla \(\PageIndex{2}\), obtenemos:

\[\begin {align*}
ΔH&=[1080+2(436)]−[3(415)+350+464]\\
&=\ce{−107\:kJ}
\end {align*}\]

Podemos comparar este valor con el valor calculado en base a los datos \(ΔH^\circ_\ce f\) del Apéndice G:

\[\begin {align*}
ΔH&=[ΔH^\circ_{\ce f}\ce{CH3OH}(g)]−[ΔH^\circ_{\ce f}\ce{CO}(g)+2×ΔH^\circ_{\ce f}\ce{H2}]\\
&=[−201.0]−[−110.52+2×0]\\
&=\mathrm{−90.5\:kJ}
\end {align*}\]

Tenga en cuenta que existe una diferencia bastante significativa entre los valores calculados usando los dos métodos diferentes. Esto ocurre porque los valores de D son el promedio de diferentes fuerzas de unión; por lo tanto, a menudo solo están aproximadamente de acuerdo con otros datos.

Ejercicio \(\PageIndex{1}\)

El alcohol etílico, CH₃CH₂OH, fue uno de los primeros químicos orgánicos sintetizados deliberadamente por los humanos. Tiene muchos usos en la industria, y es el alcohol contenido en las bebidas alcohólicas. Se puede obtener por fermentación de azúcar o se sintetiza por hidratación de etileno en la siguiente reacción:

Usando las energías de enlace en la Tabla \(\PageIndex{2}\), calcule un cambio aproximado de entalpía, ΔH, para esta reacción.

Respuesta

–35 kJ

Fuerza de enlace iónico y energía reticular

Un compuesto iónico es estable debido a la atracción electrostática entre sus iones positivos y negativos. La energía reticular de un compuesto es una medida de la fuerza de esta atracción. La energía reticular (\(ΔH_{retícula}\)) de un compuesto iónico se define como la energía requerida para separar un mol del sólido en sus iones gaseosos componentes. Para el MX iónico sólido, la energía reticular es el cambio de entalpía del proceso:

\[MX_{(s)}⟶Mn^+_{(g)}+X^{n−}_{(g)} \;\;\;\;\; ΔH_{lattice} \label{EQ6}\]

Tenga en cuenta que estamos usando la convención donde el sólido iónico se separa en iones, por lo que nuestras energías reticulares serán endotérmicas (valores positivos). Algunos textos usan la convención equivalente pero opuesta, que define la energía de la red como la energía liberada cuando los iones separados se combinan para formar una red y dan valores negativos (exotérmicos). Por lo tanto, si está buscando energías reticulares en otra referencia, asegúrese de verificar qué definición esta usando. En ambos casos, una magnitud mayor para la energía reticular indica un compuesto iónico más estable. Para cloruro de sodio, ΔH_lattice = 769 kJ. Por lo tanto, requiere 769 kJ para separar un mol de NaCl sólido en iones de Na ⁺ y Cl^– gaseosos. Cuando un mol de cada uno de los iones gaseosos de Na⁺ y Cl^– forma NaCl sólido, se liberan 769 kJ de calor.

La energía reticular \(ΔH_{retícula}\) de un cristal iónico se puede expresar mediante la siguiente ecuación (derivada de la ley de Coulomb, que rige las fuerzas entre cargas eléctricas):

\[ΔH_{lattice}=\dfrac{C(Z^+)(Z^−)}{R_o} \label{EQ7}\]

en el cual

• \(\ce{C}\) es un constante que depende del tipo de estructura cristalina;
• \(Z^+\) y \(Z^-\) son las cargas en los iones; y
• \(R_o\) es la distancia interiónica (la suma de los radios de los iones positivos y negativos).

Por lo tanto, la energía reticular de un cristal iónico aumenta rápidamente a medida que aumentan las cargas de los iones y disminuyen los tamaños de los iones. Cuando todos los demás parámetros se mantienen constantes, duplicar la carga tanto del catión como del anión cuadruplica la energía de la red. Por ejemplo, la energía reticular de LiF (Z⁺ y Z^– = 1) es 1023 kJ/mol, mientras que la de MgO (Z ⁺ y Z^– = 2) es 3900 kJ/mol (R_o es casi la misma, alrededor de 200 pm para ambos compuestos).

Diferentes distancias interatómicas producen diferentes energías reticulares. Por ejemplo, podemos comparar la energía de la red de MgF₂ (2957 kJ/mol) con la de MgI₂ (2327 kJ/mol) para observar el efecto sobre la energía de red del tamaño iónico más pequeño de F^– en comparación con I^–.

Ejemplo \(\PageIndex{2}\): Comparaciones de energía reticular

La preciosa gema rubí es el óxido de aluminio, Al₂O₃, que contiene trazas de Cr³⁺. El compuesto Al₂Se₃ se usa en la fabricación de algunos dispositivos semiconductores. ¿Cual tiene la energía de red más grande, Al₂O₃ o Al₂Se₃?

Solución

En estos dos compuestos iónicos, las cargas Z ⁺ y Z^– son las mismas, por lo que la diferencia en la energía de la red dependerá principalmente de R^o. El ion O₂ es más pequeño que el ion Se₂. Por lo tanto, Al₂O₃ tendría una distancia interiónica más corta que Al₂Se₃, y Al₂O₃ tendría la energía reticular más grande.

Ejercicio \(\PageIndex{2}\)

El óxido de zinc, ZnO, es un protector solar muy efectivo. ¿Cómo se compararía la energía reticular de ZnO con la de NaCl?

Respuesta

El compuesto ZnO tendría la energía de red más grande porque los valores Z tanto del catión como del anión en ZnO son mayores, y la distancia interiónica de ZnO es menor que la del NaCl.

El Ciclo de Born-Haber

No es posible medir las energías de la red directamente. Sin embargo, la energía de la red se puede calcular usando la ecuación dada en la sección anterior o usando un ciclo termoquímico. El ciclo de Born-Haber es una aplicación de la ley de Hess que descompone la formación de un sólido iónico en una serie de pasos individuales:

• \(ΔH^\circ_\ce f\), la entalpía estándar de formación del compuesto
• IE, la energía de ionización del metal
• EA, la afinidad electrónica del no metal \(ΔH^\circ_s\), la entalpía de sublimación del metal
• D, la energía de disociación de enlace del no metal
• ΔH_lattice, la energía reticular del compuesto

Figura \(\PageIndex{1}\) diagramas del ciclo de Born-Haber para la formación de fluoruro de cesio sólido.

Figura \(\PageIndex{1}\): El ciclo de Born-Haber muestra las energías relativas de cada paso involucrado en la formación de un sólido iónico a partir de los elementos necesarios en sus estados de referencia.

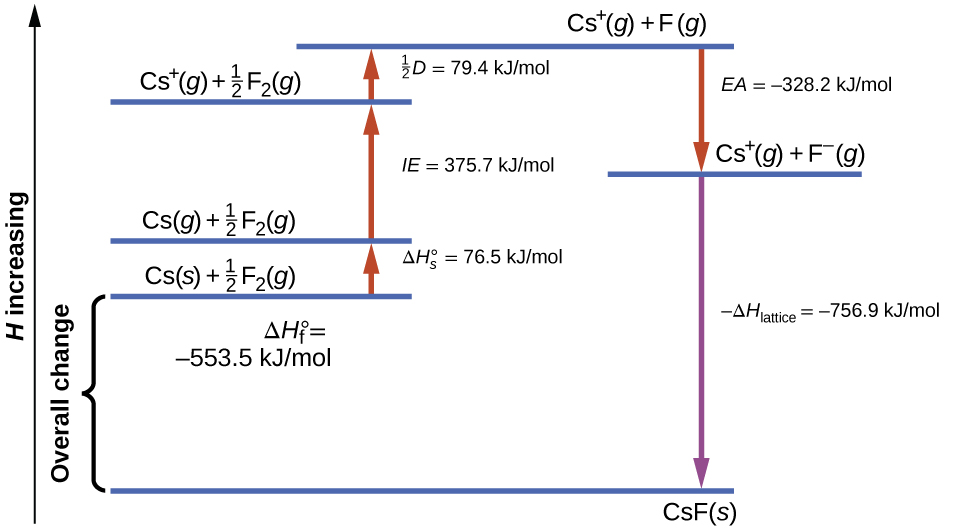
Comenzamos con los elementos en sus estados más comunes, Cs_(s) y F_2(g). El \(\Delta H^\ circ_\ce s\) representa la conversión de cesio sólido en un gas, y luego la energía de ionización convierte los átomos de cesio gaseoso en cationes. En el siguiente paso, tenemos en cuenta la energía requerida para romper el enlace F – F para producir átomos de flúor. La conversión de un mol de átomos de flúor en iones fluoruro es un proceso exotérmico, por lo que este paso emite energía (la afinidad electrónica) y se muestra como decreciente a lo largo del eje y. Ahora tenemos un mol de cationes Cs y un mol de aniones F. Estos iones se combinan para producir fluoruro de cesio sólido. El cambio de entalpía en este paso es el negativo de la energía de la red, por lo que también es una cantidad exotérmica. La energía total involucrada en esta conversión es igual a la entalpía de formación determinada experimentalmente, \(ΔH^\circ_\ce f \), del compuesto a partir de sus elementos. En este caso, el cambio general es exotérmico.

La ley de Hess también se puede usar para mostrar la relación entre las entalpías de los pasos individuales y la entalpía de la formación. La tabla \(\PageIndex{3}\) muestra esto para el fluoruro de cesio, CsF.

Tabla\(\PageIndex{3}\): Entalpías de transiciones selectas

Entalpía de sublimación de Cs(s)	\(\ce{Cs}(s)⟶\ce{Cs}(g)\hspace{20px}ΔH=ΔH^\circ_s=\mathrm{77\:kJ/mol}\)
La mitad de la energía de enlace de F2	\(\dfrac{1}{2}\ce{F2}(g)⟶\ce{F}(g)\hspace{20px}ΔH=\dfrac{1}{2}D=\mathrm{79\:kJ/mol}\)
Energía de ionización de Cs(g)	\(\ce{Cs}(g)⟶\ce{Cs+}(g)+\ce{e-}\hspace{20px}ΔH=IE=\ce{376\:kJ/mol}\)
Negativo de la afinidad electrónica de F	\(\ce{F}(g)+\ce{e-}⟶\ce{F-}(g)\hspace{20px}ΔH=−EA=\ce{-328\:kJ/mol}\)
Negativo de la energía reticular de CsF(s)	\(\ce{Cs+}(g)+\ce{F-}(g)⟶\ce{CsF}(s)\hspace{20px}ΔH=−ΔH_\ce{lattice}=\:?\)
Entalpía de formación de CsF(s), sume pasos 1–5	\(ΔH=ΔH^\circ_f=ΔH^\circ_s+\dfrac{1}{2}D+IE+(−EA)+(−ΔH_\ce{lattice})\) \(\ce{Cs}(s)+\dfrac{1}{2}\ce{F2}(g)⟶\ce{CsF}(s)=\ce{-554\:kJ/mol}\)

Por lo tanto, la energía reticular se puede calcular a partir de otros valores. Para el cloruro de cesio, usando estos datos, la energía reticular es:

\[ΔH_\ce{lattice}=\mathrm{(411+109+122+496+368)\:kJ=770\:kJ}\]

El ciclo de Born-Haber también se puede usar para calcular cualquiera de las otras cantidades en la ecuación para la energía reticular, siempre que se sepa el resto. Por ejemplo, si la entalpía relevante de sublimación \(ΔH^\circ_s\), la energía de ionización (IE), la entalpía de disociación de enlace (D), la energía reticular ΔH_lattice y la entalpía estándar de formación \(ΔH^\circ_\cef\) se saben, el ciclo de Born-Haber se puede usar para determinar la afinidad electrónica de un átomo.

Las energías reticulares calculadas para compuestos iónicos son típicamente mucho más grandes que las energías de disociación de enlaces medidas para enlaces covalentes. Como las energías reticulares generalmente caen en el rango de 600–4000 kJ/mol (algunas incluso más altas), las energías de disociación de enlaces covalentes están típicamente entre 150–400 kJ/mol para enlaces simples. Sin embargo, tenga en cuenta que estos no son valores directamente comparables. Para los compuestos iónicos, las energías reticulares están asociadas con muchas interacciones, ya que los cationes y los aniones se agrupan en una red extendida. Para enlaces covalentes, la energía de disociación de enlaces está asociada con la interacción de solo dos átomos.

Resumen

La fuerza de un enlace covalente se mide por su energía de disociación de enlace, es decir, la cantidad de energía requerida para romper ese enlace particular en un mol de moléculas. Los enlaces múltiples son más fuertes que los enlaces simples entre los mismos átomos. La entalpía de una reacción se puede estimar en función de la entrada de energía requerida para romper los enlaces y la energía liberada cuando se forman nuevos enlaces. Para los enlaces iónicos, la energía reticular es la energía requerida para separar un mol de un compuesto en sus iones de fase gaseosa. La energía reticular aumenta para los iones con cargas más altas y distancias más cortas entre iones. A menudo, las energías reticulares se calculan usando el ciclo de Born-Haber, un ciclo termoquímico que incluye todos los pasos energéticos involucrados en la conversión de elementos en un compuesto iónico.

Ecuaciones Clave

• Energía de enlace para una molécula diatómica: \(\ce{XY}(g)⟶\ce{X}(g)+\ce{Y}(g)\hspace{20px}\ce{D_{X–Y}}=ΔH°\)
• Cambio de entalpía: ΔH = ƩD_{bonds broken} – ƩD_{bonds formed}
• Energía reticular para un sólido MX: \(\ce{MX}(s)⟶\ce M^{n+}(g)+\ce X^{n−}(g)\hspace{20px}ΔH_\ce{lattice}\)
• Energía reticular para un cristal iónico: \(ΔH_\ce{lattice}=\mathrm{\dfrac{C(Z^+)(Z^-)}{R_o}}\)

Notas al Pie de la Página

1. Esta pregunta está tomada del Examen de Colocación Avanzada de Química y se usa con el permiso del Servicio de Pruebas Educativas.

Glosario

energía de enlace

(también, energía de disociación de enlace) energía requerida para romper un enlace covalente en una sustancia gaseosa

Ciclo de Born-Haber

ciclo termoquímico que relaciona los diversos pasos energéticos involucrados en la formación de un sólido iónico a partir de los elementos relevantes

energía reticular (ΔH_lattice)

energía requerida para separar un mol de un sólido iónico en sus iones gaseosos componentes

Contribuyentes

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.