7.4: Las cargas formales y la resonancia
- Page ID
- 1856
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
• Calcular las cargas formales para átomos en cualquier estructura de Lewis
• Usar las cargas formales para identificar la estructura de Lewis más razonable para una molécula dada
• Explicar el concepto de resonancia y dibujar estructuras de Lewis que representen formas de resonancia para una molécula dada
Anteriormente, discutimos cómo escribir estructuras de Lewis para moléculas e iones poliatómicos. Sin embargo, en algunos casos hay más de una estructura válida para una molécula. Podemos usar el concepto de cargas formales para ayudarnos a predecir la estructura de Lewis más apropiada cuando más de una es razonable.
Cálculo de la carga formal
La carga formal de un átomo en una molécula es la carga hipotética que tendría el átomo si pudiéramos redistribuir los electrones en los enlaces de manera uniforme entre los átomos. Otra forma de decir esto es que la carga formal resulta cuando tomamos la cantidad de electrones de valencia de un átomo neutro, restamos los electrones sin enlace y luego restamos la cantidad de enlaces conectados a ese átomo en la estructura de Lewis.
Así, calculamos la carga formal de la siguiente manera:
Podemos verificar los cálculos de las cargas formales determinando la suma de las cargas formales para toda la estructura. La suma de las cargas formales de todos los átomos en una molécula debe ser cero; la suma de las cargas formales en un ion debe ser igual a la carga del ion.
Debemos recordar que la carga formal calculada para un átomo no es la carga real del átomo en la molécula. El cargo formal es solo un procedimiento útil de contabilidad; no indica la presencia de cargos reales.
Ejemplo \(\PageIndex{1}\): Cálculo de la carga formal a partir de las estructuras de Lewis
Asigne las cargas formales a cada átomo en el ion interhalógeno \(\ce{ICl4-}\).
Solución
Dividimos los pares de electrones de enlace por igual para todos los enlaces de \(\ce{I–Cl}\):
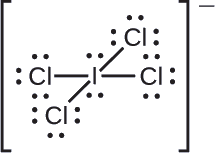
Asignamos pares solitarios de electrones a sus átomos. Cada átomo de Cl ahora tiene siete electrones asignados, y el átomo I tiene ocho electrones.
Reste este número del número de electrones de valencia para el átomo neutro:
- I: 7 – 8 = –1
- Cl: 7 – 7 = 0
La suma de las cargas formales de todos los átomos es igual a –1, que es idéntica a la carga del ion (–1).
Ejercicio \(\PageIndex{1}\)
Calcule la carga formal para cada átomo en la molécula de monóxido de carbono:

- Respuesta
-
C −1, O +1
Ejemplo \(\PageIndex{2}\): Cálculo de la carga formal a partir de las estructuras de Lewis
Asigne las cargas formales a cada átomo en el ion interhalógeno \(\ce{BrCl3}\).
Solución
Asigne uno de los electrones en cada enlace de Br – Cl al átomo Br y uno al átomo Cl en ese enlace:
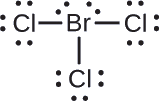
Asigne los pares solitarios a su átomo. Ahora cada átomo de Cl tiene siete electrones y el átomo de Br tiene siete electrones.
Reste este número del número de electrones de valencia para el átomo neutro. Esto le da la carga formal:
- Br: 7 – 7 = 0
- Cl: 7 – 7 = 0
Todos los átomos en \(\ce{BrCl3}\) tienen una carga formal de cero, y la suma de las cargas formales totaliza cero, como debe ser en una molécula neutra.
Ejercicio \(\PageIndex{2}\)
Determine la carga formal para cada átomo en \(\ce{NCl3}\).
- Respuesta
-
N: 0; todos los átomos de Cl: 0
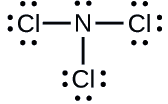
Usando la carga formal para predecir la estructura molecular
La disposición de los átomos en una molécula o ion se llama la estructura molecular. En muchos casos, seguir los pasos para escribir las estructuras de Lewis puede resultar en más de una posible estructura molecular; por ejemplo, diferentes enlaces múltiples y colocaciones de electrones de pares solitarios o diferentes disposiciones de átomos. Algunas pautas relacionadas con la carga formal pueden ser útiles para decidir cuál de las posibles estructuras es más probable para una molécula o ion particular.
Directrices de predicción de la estructura molecular
- Una estructura molecular en la que todas las cargas formales son cero es preferible a una en la que algunas cargas formales son distantes a cero.
- Si la estructura de Lewis debe tener cargas formales que no son cero, es preferible el arreglo con las cargas formales más cercas a cero.
- Las estructuras de Lewis son preferibles cuando las cargas formales adyacentes son cero o del signo opuesto.
- Cuando debemos elegir entre varias estructuras de Lewis con distribuciones similares de cargas formales, es preferible la estructura con las cargas formales negativas en los átomos más electronegativos.
Para ver cómo se aplican estas pautas, consideremos algunas estructuras posibles para el dióxido de carbono, \(\ce{CO2}\). Sabemos por nuestra discusión previa que el átomo menos electronegativo generalmente ocupa la posición central, pero las cargas formales nos permiten entender por qué ocurre esto. Podemos dibujar tres posibilidades para la estructura: carbono en el centro y enlaces dobles, carbono en el centro con un enlace simple y triple, y el oxígeno en el centro con enlaces dobles:
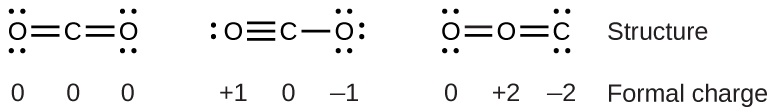
Comparando las tres cargas formales, podemos identificar definitivamente la estructura de la izquierda como preferible porque solo tiene cargas formales de cero (Directriz 1).
Como otro ejemplo, el ion tiocianato, un ion formado a partir de un átomo de carbono, un átomo de nitrógeno y un átomo de azufre, podría tener tres estructuras moleculares diferentes: \(\ce{CNS^{–}}\), \(\ce{NCS^{–}}\), o \(\ce{CSN^{–}}\). Las cargas formales presentes en cada una de estas estructuras moleculares pueden ayudarnos a elegir la disposición más probable de los átomos. Las posibles estructuras de Lewis y las cargas formales para cada una de las tres estructuras posibles para el ion tiocianato se muestran aquí:
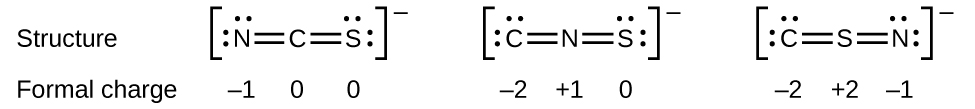
Tenga en cuenta que la suma de las cargas formales en cada caso es igual a la carga del ion (–1). Sin embargo, se prefiere la primera disposición de los átomos porque tiene el menor número de átomos con cargas formales distintas de cero (Directriz 2). Además, coloca el átomo menos electronegativo en el centro y la carga negativa en el elemento más electronegativo (Directriz 4).
Ejemplo \(\PageIndex{3}\): Uso de la carga formal para determinar la estructura molecular
Óxido nitroso, N2O, comúnmente conocido como el gas de la risa, se usa como anestésico en cirugías menores, como la extracción de rutina de las muelas del juicio. ¿Cuál es la estructura probable para el óxido nitroso?

Solución
La determinación de la carga formal produce lo siguiente:
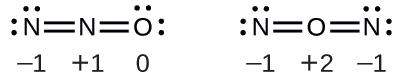
La estructura con un átomo de oxígeno terminal satisface mejor los criterios para la distribución más estable de la carga formal:
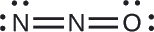
El número de átomos con cargas formales se minimiza (Directriz 2), y no hay carga formal mayor que uno (Directriz 2). Esto es de nuevo consistente con la preferencia por tener el átomo menos electronegativo en la posición central.
Ejercicio \(\PageIndex{3}\)
¿Cuál es la estructura molecular más probable para el ion nitrito (\(\ce{NO2-}\))?
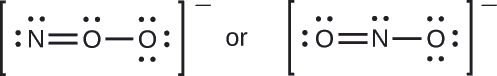
- Respuesta
-
\(\ce{ONO^{–}}\)
Resonancia
Es posible que haya notado que el anión nitrito en el Ejemplo \(\PageIndex{3}\) puede tener dos estructuras posibles con los átomos en las mismas posiciones. Los electrones involucrados en el doble enlace N – O, sin embargo, están en diferentes posiciones:
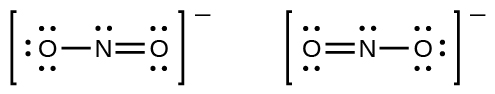
Si los iones nitrito contienen un enlace simple y uno doble, esperaríamos que las dos longitudes de enlace sean diferentes. Un enlace doble entre dos átomos es más corto (y más fuerte) que un enlace simple entre los mismos dos átomos. Sin embargo, los experimentos muestran que ambos enlaces N–O en \(\ce{NO2-}\) tienen la misma fuerza y longitud, y son idénticos en todas las demás propiedades.
No es posible escribir una sola estructura de Lewis para \(\ce{NO2-}\) en la que el nitrógeno tenga un octeto y ambos enlaces sean equivalentes. En su lugar, usamos el concepto de resonancia: si dos o más estructuras de Lewis con la misma disposición de átomos se pueden escribir para una molécula o ion, la distribución real de electrones es un promedio de la que muestran las diversas estructuras de Lewis. La distribución real de electrones en cada uno de los enlaces nitrógeno-oxígeno en \(\ce{NO2-}\) es el promedio de un enlace doble y un enlace simple. Llamamos a las estructuras individuales de Lewis formas de resonancia. La estructura electrónica real de la molécula (el promedio de las formas de resonancia) se llama un híbrido de resonancia de las formas de resonancia individuales. Una flecha de dos puntas entre las estructuras de Lewis indica que son formas de resonancia. Por lo tanto, la estructura electrónica del ion \(\ce{NO2-}\) se muestra como:
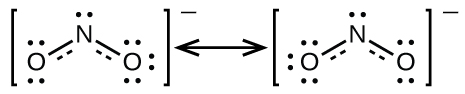
Debemos recordar que una molécula descrita como un híbrido de resonancia nunca posee una estructura electrónica descrita por cualquiera de las formas de resonancia. No fluctúa entre las formas de resonancia; más bien, la estructura electrónica real es siempre la media de la que muestran todas las formas de resonancia. George Wheland, uno de los pioneros de la teoría de la resonancia, usó una analogía histórica para describir la relación entre las formas de resonancia y los híbridos de resonancia. Un viajero medieval, que nunca había visto un rinoceronte, lo describió como un híbrido de un dragón y un unicornio porque tenía muchas propiedades en común con ambos. Así como un rinoceronte no es un dragón a veces ni un unicornio en otras ocasiones, un híbrido de resonancia no es ninguna de sus formas de resonancia en un momento dado. Como un rinoceronte, es una entidad real que la evidencia experimental ha demostrado que existe. Tiene algunas características en común con sus formas de resonancia, pero las formas de resonancia son imágenes convenientes e imaginarias (como el unicornio y el dragón).
El anión carbonato \(\ce{CO3^2-}\), Nos da un segundo ejemplo de la resonancia:
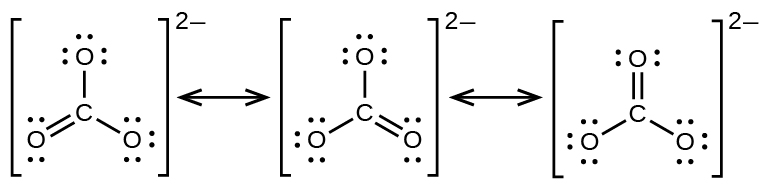
Un átomo de oxígeno debe tener un doble enlace con el carbono para completar el octeto en el átomo central. Sin embargo, todos los átomos de oxígeno son equivalentes, y el doble enlace se podría formar a partir de cualquiera de los tres átomos. Esto da lugar a tres formas de resonancia del ion carbonato. Como podemos escribir tres estructuras de resonancia idénticas, sabemos que la disposición real de los electrones en el ion carbonato es el promedio de las tres estructuras. Una vez más, los experimentos muestran que los tres enlaces C – O son exactamente iguales.
Resumen
En una estructura de Lewis, se pueden asignar cargas formales a cada átomo tratando cada enlace como si la mitad de los electrones estuvieran asignados a cada átomo. Estos cargos formales hipotéticos son una guía para determinar la estructura de Lewis más apropiada. Se prefiere una estructura en la que los cargos formales sean lo más cercanos posible a cero. La resonancia ocurre en los casos en que se pueden escribir dos o más estructuras de Lewis con arreglos idénticos de átomos pero diferentes distribuciones de electrones. La distribución real de electrones (el híbrido de resonancia) es un promedio de la distribución indicada por las estructuras individuales de Lewis (las formas de resonancia).
Ecuaciones Clave
- \(\textrm{formal charge = # valence shell electrons (free atom) − # one pair electrons − }\dfrac{1}{2}\textrm{ # bonding electrons}\)
Glosario
- carga formal
- La carga que resultaría en un átomo tomando la cantidad de electrones de valencia en el átomo neutro y restando los electrones no unidos y la cantidad de enlaces (la mitad de los electrones en enlace).
- estructura molecular
- La disposición de los átomos en una molécula o ion.
- resonancia
- La situación en la que una estructura de Lewis es insuficiente para describir el enlace en una molécula y se observa el promedio de estructuras múltiples.
- formas de resonancia
- Dos o más estructuras de Lewis que tienen la misma disposición de átomos pero diferentes disposiciones de electrones.
- híbrido de resonancia
- Promedio de las formas de resonancia mostradas por las estructuras individuales de Lewis.
Contribuyentes
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


