7.6: La estructura molecular y la polaridad

habilidades para desarrollar

• Predecir las estructuras de moléculas pequeñas usando la teoría de la valencia de la repulsión del par de electrones (VSEPR)
• Explicar los conceptos de enlaces covalentes polares y polaridad molecular.
• Evaluar la polaridad de una molécula en función de su unión y estructura.

Hasta ahora, hemos usado estructuras de Lewis bidimensionales para representar moléculas. Sin embargo, la estructura molecular es en realidad tridimensional, y es importante poder describir los enlaces moleculares en términos de sus distancias, ángulos y disposiciones relativas en el espacio (Figura \(\PageIndex{1}\)). Un ángulo de enlace es el ángulo entre dos enlaces que comprenden un átomo común, generalmente medido en grados. Una distancia de enlace (o longitud de enlace) es la distancia entre los núcleos de dos átomos unidos a lo largo de la línea recta que une los núcleos. Las distancias de enlace se miden en Ångstroms (1 Å = 10^–10 m) o picómetros (1 pm = 10^–12 m, 100 pm = 1 Å).

Figura \(\PageIndex{1}\): Las distancias de enlace (longitudes) y los ángulos se muestran para la molécula de formaldehído, H₂CO.

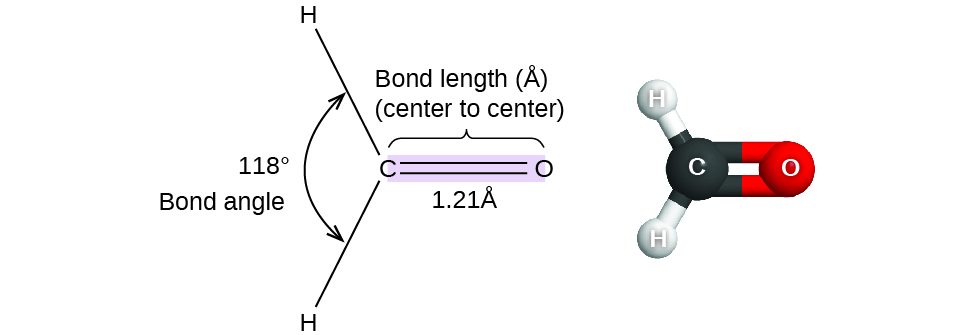
La Teoría de VSEPR

La teoría de la repulsión de pares de electrones de valencia (teoría VSEPR) nos permite predecir la estructura molecular, incluidos los ángulos de enlace aproximados alrededor de un átomo central, de una molécula a partir de un examen del número de enlaces y pares de electrones solitarios en su estructura de Lewis. El modelo VSEPR supone que los pares de electrones en la capa de valencia de un átomo central adoptarán una disposición que minimice las repulsiones entre estos pares de electrones al maximizar la distancia entre ellos. Los electrones en la capa de valencia de un átomo central forman pares de electrones de enlace, ubicados principalmente entre átomos unidos, o pares solitarios. La repulsión electrostática de estos electrones se reduce cuando las diversas regiones de alta densidad electrónica asumen posiciones lo más alejadas posible.

La teoría VSEPR predice la disposición de los pares de electrones alrededor de cada átomo central y, por lo general, la disposición correcta de los átomos en una molécula. Sin embargo, debemos entender que la teoría solo considera las repulsiones de pares de electrones. Otras interacciones, como las repulsiones nuclear-nucleares y las atracciones de electrones nucleares, también están involucradas en la disposición final que los átomos adoptan en una estructura molecular particular.

Como un ejemplo simple de la teoría VSEPR, vamos a predecir la estructura de una molécula gaseosa de BeF₂. La estructura de Lewis de BeF₂ (Figura \(\PageIndex{2}\)) muestra solo dos pares de electrones alrededor del átomo central de berilio. Con dos enlaces y sin pares solitarios de electrones en el átomo central, los enlaces están lo más separados posible, y la repulsión electrostática entre estas regiones de alta densidad de electrones se reduce al mínimo cuando están en lados opuestos del átomo central. El ángulo de enlace es180° (Figura \(\PageIndex{2}\)).

Figura \(\PageIndex{2}\): La moleula BeF₂ adopta una estructura lineal en la que los dos enlaces están lo más separados posible, en lados opuestos del átomo Be.

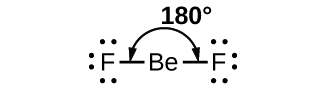
Figura \(\PageIndex{3}\) ilustra esta y otras geometrías de pares de electrones que minimizan las repulsiones entre regiones de alta densidad de electrones (enlaces y/o pares solitarios). Dos regiones de densidad electrónica alrededor de un átomo central en una molécula forman una geometría lineal; tres regiones forman una geometría plana trigonal; cuatro regiones forman una geometría tetraédrica; cinco regiones forman una geometría bipiramidal trigonal; y seis regiones forman una geometría octaédrica.

Figura \(\PageIndex{3}\): Las geometrías básicas de pares de electrones predichas por la teoría VSEPR maximizan el espacio alrededor de cualquier región de densidad de electrones (enlaces o pares solitarios).

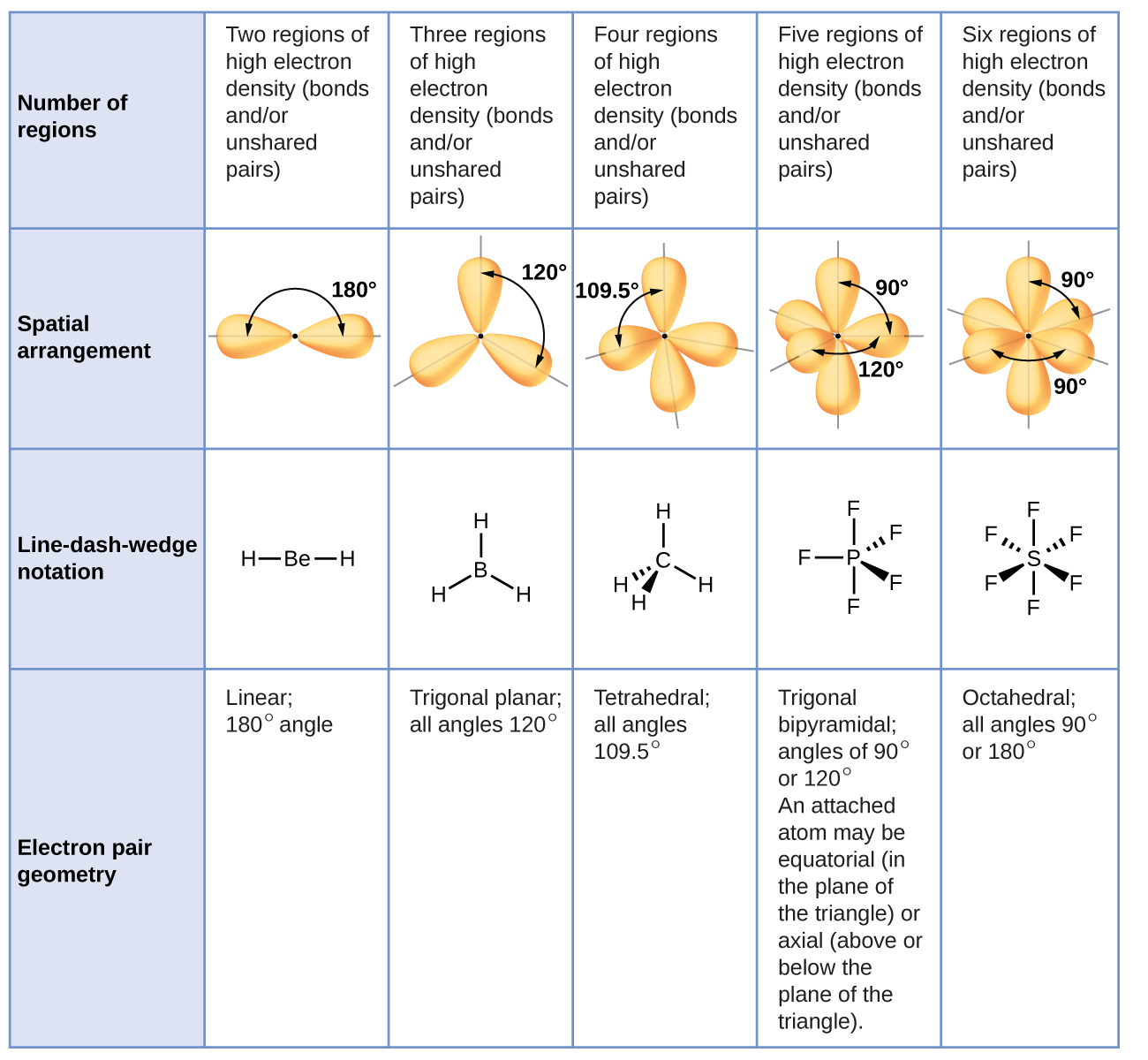
Geometría de pares de electrones versus estructura molecular

Es importante tener en cuenta que la geometría de pares de electrones alrededor de un átomo central no es lo mismo que su estructura molecular. Las geometrías de pares de electrones que se muestran en la Figura \(\PageIndex{3}\) describen todas las regiones donde se encuentran los electrones, los enlaces y los pares solitarios. La estructura molecular describe la ubicación de los átomos, no de los electrones.

Diferenciamos entre estas dos situaciones nombrando la geometría que incluye todos los pares de electrones, la geometría de pares de electrones. La estructura que incluye solo la colocación de los átomos en la molécula se llama la estructura molecular. Las geometrías de los pares de electrones serán las mismas que las estructuras moleculares cuando no haya pares de electrones solitarios alrededor del átomo central, pero serán diferentes cuando haya pares solitarios presentes en el átomo central.

Figura \(\PageIndex{4}\): La estructura molecular de la molécula del metano, CH₄, se muestra con una disposición tetraédrica de los átomos de hidrógeno. A veces, las estructuras VSEPR como esta, se dibujan usando la notación de cuña y guión, en la que las líneas continuas representan enlaces en el plano de la página, las cuñas sólidas representan enlaces que salen del plano y las líneas discontinuas representan enlaces que bajan al plano.

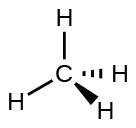
Por ejemplo, la molécula del metano, CH₄, que es el componente principal del gas natural, tiene cuatro pares de electrones de enlace alrededor del átomo de carbono central; la geometría del par de electrones es tetraédrica, al igual que la estructura molecular (Figura \(\PageIndex{4}\)). Por otro lado, la molécula de amoníaco, NH₃, también tiene cuatro pares de electrones asociados con el átomo de nitrógeno, y por lo tanto tiene una geometría tetraédrica de pares de electrones. Sin embargo, una de estas regiones es un par solitario, que no está incluido en la estructura molecular, y este par solitario influye en la forma de la molécula (Figura \(\PageIndex{5}\)).

Figura \(\PageIndex{5}\): (a) La geometría del par de electrones para la molécula del amoníaco es tetraédrica con un par solitario y tres enlaces simples. (b) La estructura molecular piramidal trigonal se determina a partir de la geometría del par de electrones. (c) Los ángulos de enlace reales son un poco diferente de los ángulos idealizados porque el par solitario ocupa una región de espacio más grande que los enlaces simples, lo que hace que el ángulo HNH sea un poco más pequeño que 109.5°.

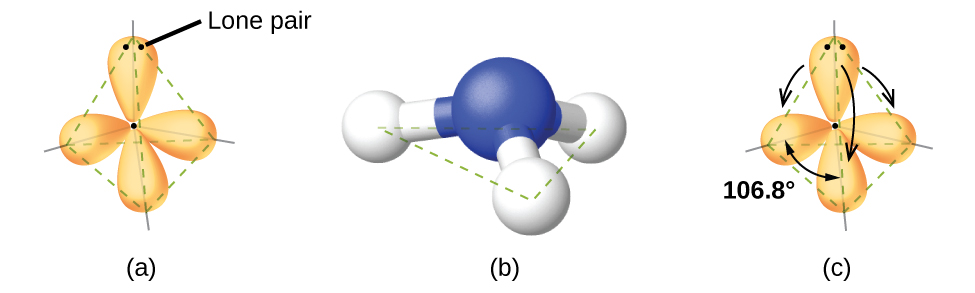
Pequeñas distorsiones desde los ángulos ideales en la Figura \(\PageIndex{5}\) pueden resultar de diferencias en la repulsión entre varias regiones de densidad de electrones. La teoría VSEPR predice estas distorsiones al establecer un orden de repulsiones y un orden de la cantidad de espacio ocupado por diferentes tipos de pares de electrones. El orden de las repulsiones de pares de electrones de mayor a menor repulsión es:

par solitario-par solitario > par solitario-par de unión > par de unión-par de unión

Este orden de repulsiones determina la cantidad de espacio ocupado por diferentes regiones de electrones. Un par solitario de electrones ocupa una región más grande del espacio que los electrones en un enlace triple; en turno, los electrones en un enlace triple ocupan más espacio que aquellos en un enlace doble, y así sucesivamente. El orden de tamaños de mayor a menor es:

par solitario > triple enlace > doble enlace > enlace simple

Considere el formaldehído, H₂CO, que se usa como conservante para muestras biológicas y anatómicas. Esta molécula tiene regiones de alta densidad de electrones que consisten en dos enlaces simples y un enlace doble. La geometría básica es trigonal plana con ángulos de enlace de 120 °, pero vemos que el doble enlace causa ángulos un poco más grandes (121 °), y el ángulo entre los enlaces simples es un poco más pequeño (118 °).

En la molécula de amoníaco, los tres átomos de hidrógeno unidos al nitrógeno central no están dispuestos en una estructura molecular plana trigonal, sino más bien en una estructura molecular pirámide trigonal tridimensional (Figura \(\PageIndex{6}\)) con el nitrógeno átomo en el ápice y los tres átomos de hidrógeno que forman la base. Los ángulos de enlace ideales en una pirámide trigonal se basan en la geometría del par de electrones tetraédricos. Nuevamente, hay desviaciones del ideal porque los pares solitarios ocupan regiones más grandes del espacio que los electrones en un enlace. Los ángulos de enlace H - N - H en NH₃ son un poco más pequeños que el ángulo de 109.5 ° en un tetraedro regular (Figura \(\PageIndex{6}\)) porque la repulsión del par de unión-pares solitarios es mayor que la repulsión de par de unión- par de unión. Las estructuras moleculares ideales se predicen en función de las geometrías de pares de electrones para diversas combinaciones de pares solitarios y pares de enlace.

Figura \(\PageIndex{6}\): Las estructuras moleculares son idénticas a las geometrías de pares de electrones cuando no hay pares de electrones solos presentes (primera columna). Para un número particular de pares de electrones (fila), las estructuras moleculares para uno o más pares solitarios se determinan en función de las modificaciones de la geometría de pares de electrones correspondiente.

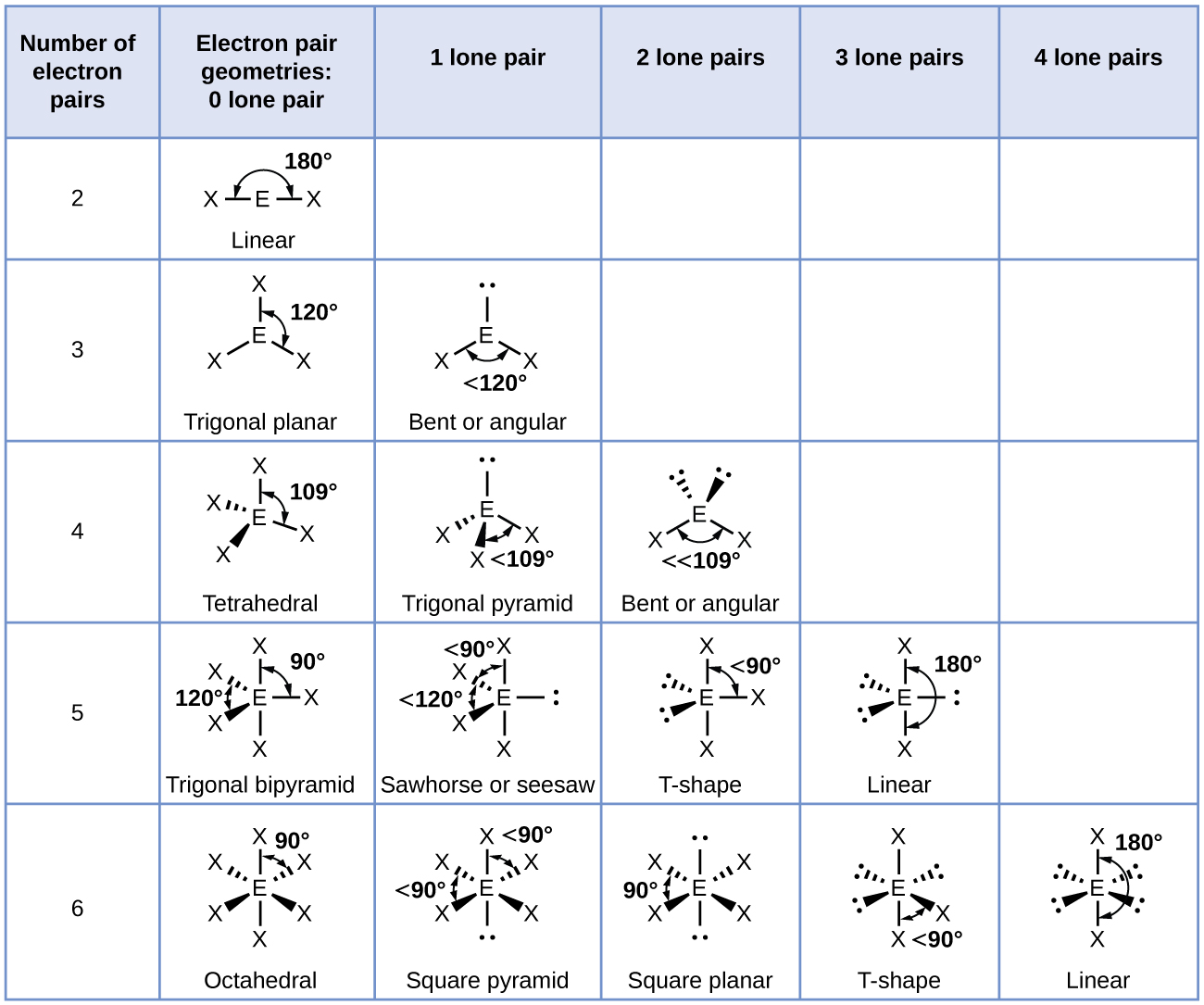
De acuerdo con la teoría VSEPR, las ubicaciones atómicas terminales (Xs en la Figura \(\PageIndex{7}\)) son equivalentes dentro de las geometrías lineales, planas trigonales y de pares de electrones tetraédricos (las primeras tres filas de la tabla). No importa qué X se reemplaza con un par solitario porque las moléculas se pueden rotar para convertir posiciones. Sin embargo, para las geometrías de pares de electrones bipiramidales trigonales, hay dos posiciones X distintas (Figura \(\PageIndex{7}\) a): una posición axial (si tenemos un modelo de una bipirámide trigonal en las dos posiciones axiales, tener un eje alrededor del cual podemos rotar el modelo) y una posición ecuatorial (tres posiciones forman un ecuador alrededor del centro de la molécula). La posición axial está rodeada por ángulos de enlace de 90 °, mientras que la posición ecuatorial tiene más espacio disponible debido a los ángulos de enlace de 120°. En una geometría de pares de electrones bipiramidales trigonales, los pares solitarios siempre ocupan posiciones ecuatoriales porque estas posiciones más espaciosas pueden acomodar más fácilmente a los pares solitarios más grandes.

Teóricamente, podemos encontrar tres posibles arreglos para los tres enlaces y dos pares solitarios para la molécula de ClF₃ (Figura \(\PageIndex{7}\)). La estructura estable es la que coloca los pares solitarios en ubicaciones ecuatoriales, dando una estructura molecular en forma de T.

Figura \(\PageIndex{7}\): (a) En una bipirámide trigonal, las dos posiciones axiales se ubican directamente una frente a la otra, mientras que las tres posiciones ecuatoriales se ubican en una disposición triangular. (b - d) Los dos pares solitarios (líneas rojas) en ClF₃ tienen varios arreglos posibles, pero la estructura molecular en forma de T(b) es la que realmente se observa, consistente con los pares solitarios más grandes que ocupan ambas posiciones ecuatoriales.

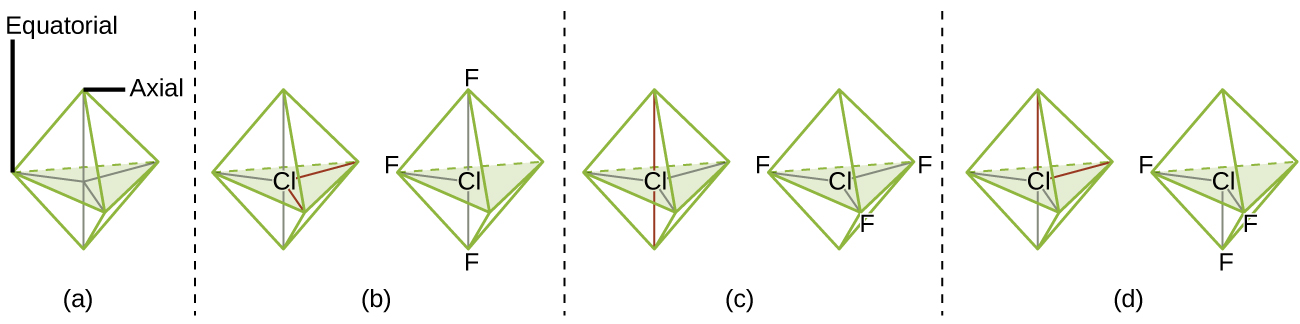
Cuando un átomo central tiene dos pares de electrones solitarios y cuatro regiones de enlace, tenemos una geometría de pares de electrones octaédricos. Los dos pares solitarios están en lados opuestos del octaedro (separados por 180°), dando una estructura molecular plana cuadrada que minimiza las repulsiones de par solitario-par solitario.

Predicción de geometría de pares de electrones y la estructura molecular

1. Escriba la estructura de Lewis de la molécula o ión poliatómico.
2. Cuente el número de regiones de densidad electrónica (pares y enlaces solitarios) alrededor del átomo central. Un enlace simple, doble o triple cuenta como una región de densidad electrónica.
3. Identifique la geometría del par de electrones en función del número de regiones de densidad de electrones: lineal, trigonal plano, tetraédrico, trigonal bipiramidal u octaédrico (Figura \(\PageIndex{7}\), primera columna).
4. Use el número de pares solitarios para determinar la estructura molecular (Figura \(\PageIndex{7}\)). Si más de un arreglo de pares solitarios y enlaces químicos es posible, elija el que minimice las repulsiones, recordando que los pares solitarios ocupan más espacio que los enlaces múltiples, que ocupan más espacio que los enlaces simples. En arreglos bipiramidales trigonales, la repulsión se minimiza cuando cada par solitario está en una posición ecuatorial. En una disposición octaédrica con dos pares solitarios, la repulsión se minimiza cuando los pares solitarios están en lados opuestos del átomo central.

Los siguientes ejemplos ilustran el uso de la teoría VSEPR para predecir la estructura molecular de las moléculas o iones que no tienen pares de electrones solitarios. En este caso, la estructura molecular es idéntica a la geometría del par de electrones.

Ejemplo \(\PageIndex{1}\): Predicción de geometría de pares de electrones y estructura molecular

Prediga la geometría de pares de electrones y la estructura molecular para cada uno de los siguientes:

1. dióxido de carbono, CO₂, una molécula producida por la combustión de combustibles fósiles
2. tricloruro de boro, BCl₃, un importante químico industrial

Solución

(a) Escribimos la estructura de Lewis de CO₂ como:

Esto nos muestra dos regiones de alta densidad de electrones alrededor del átomo de carbono: cada doble enlace cuenta como una región, y no hay pares solitarios en el átomo de carbono. Usando la teoría VSEPR, predecimos que las dos regiones de densidad electrónica se disponen en lados opuestos del átomo central con un ángulo de enlace de 180°. La geometría del par de electrones y la estructura molecular son idénticas, y las moléculas de CO₂ son lineales.

(b) Escribimos la estructura de Lewis de BCl₃ como:

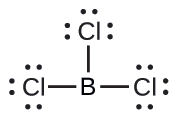
Por lo tanto, vemos que BCl₃ contiene tres enlaces, y no hay pares de electrones solitarios en el boro. La disposición de tres regiones de alta densidad de electrones da una geometría de par de electrones plana trigonal. Los enlaces B - Cl se encuentran en un plano con ángulos de 120° entre ellos. BCl₃ también tiene una estructura molecular plana trigonal.

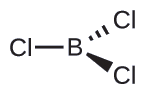
La geometría del par de electrones y la estructura molecular de BCl₃ son ambas planas trigonales. Tenga en cuenta que la geometría VSEPR indica los ángulos de enlace correctos (120°), a diferencia de la estructura de Lewis que se muestra arriba.

Ejercicio \(\PageIndex{1}\)

El carbonato, \(\ce{CO3^2-}\), es un ion poliatómico común que se encuentra en varios materiales, desde cáscaras de huevo hasta antiácidos. ¿Cuáles son la geometrías de pares de electrones y la estructura molecular de este ion poliatómico?

Respuesta

La geometría del par de electrones es trigonal plana y la estructura molecular es trigonal plana. Debido a la resonancia, los tres enlaces C - O son idénticos. Ya sea que sean simples, dobles o un promedio de los dos, cada enlace cuenta como una región de densidad de electrones.

Ejemplo \(\PageIndex{2}\): Predicción de geometría de pares de electrones y estructura molecular

Dos de los 50 principales químicos producidos en los Estados Unidos, el nitrato de amonio y el sulfato de amonio, ambos usados como fertilizantes, contienen el ion amonio. Prediga la geometría de pares de electrones y la estructura molecular del catión \(\ce{NH4+}\).

Solución

Escribimos la estructura de Lewis de \(\ce{NH4+}\) como:

Figura \(\PageIndex{7}\)).

Figura \(\PageIndex{8}\): El ion amonio muestra una geometría tetraédrica de pares de electrones, así como una estructura molecular tetraédrica.

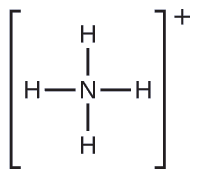
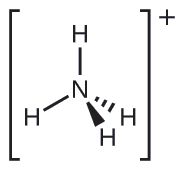
Ejercico \(\PageIndex{2}\)

Identifique una molécula con estructura molecular bipiramidal trigonal.

Respuesta

Cualquier molécula con cinco pares de electrones alrededor de los átomos centrales, incluidos los pares solitarios, será trigonal bipiramidal. \(\ce{PF5}\) es un ejemplo común.

Los siguientes ejemplos ilustran el efecto de pares de electrones solitarios en la estructura molecular.

Ejemplo \(\PageIndex{3}\): Pares solitarios en el átomo central

Prediga la geometría del par de electrones y la estructura molecular de una molécula de agua.

Solución

La estructura de Lewis de H₂O indica que hay cuatro regiones de alta densidad de electrones alrededor del átomo de oxígeno: dos pares solitarios y dos enlaces químicos:

Figura \(\PageIndex{9}\). Por lo tanto, la geometría del par de electrones es tetraédrica y la estructura molecular está en un ángulo un poco menos que 109.5 °. De hecho, el ángulo de enlace es 104.5°.

Figura\(\PageIndex{9}\): (a) H₂O tiene cuatro regiones de densidad de electrones alrededor del átomo central, por eso tiene una geometría de pares de electrones tetraédricos. (b) Dos de las regiones de electrones son pares solitarios, por eso la estructura molecular es angular.

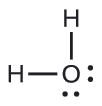
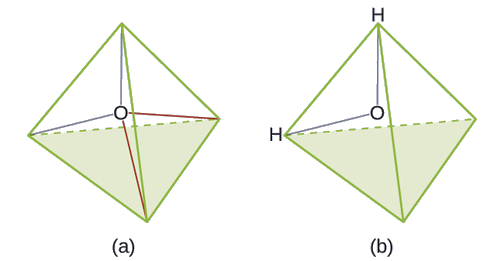
Ejercicio \(\PageIndex{3}\)

El ion hidronio, H₃O ⁺, se forma cuando los ácidos se disuelven en el agua. Prediga la geometría de pares de electrones y la estructura molecular de este catión.

Respuesta

geometría de par de electrones: tetraédrica; estructura molecular: piramidal trigonal

Ejemplo \(\PageIndex{4}\): SF₄ Tetrafluoruro de azufre

Predicción de geometría de pares de electrones y estructura molecular: SF₄ es extremadamente valioso para la preparación de compuestos que contienen flúor usados como herbicidas (es decir, SF₄ se usa como agente fluorante). Prediga la geometría del par de electrones y la estructura molecular de una molécula de SF₄.

Solución

La estructura de Lewis de SF₄ indica cinco regiones de densidad de electrones alrededor del átomo de azufre: un par solitario y cuatro pares de enlace:

Figura \(\PageIndex{10}\)).

Figura \(\PageIndex{10}\): (a) SF₄ tiene una disposición bipiramidal trigonal de las cinco regiones de densidad electrónica. (b) Una de las regiones es un par solitario, lo que da como resultado una estructura molecular en forma de balancín.

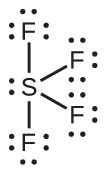
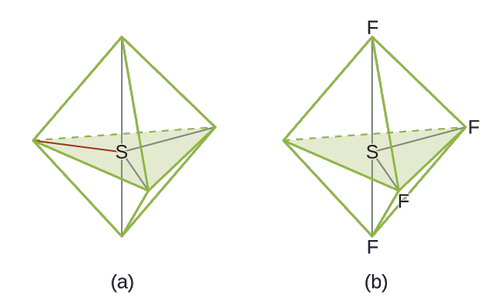
Ejercicio \(\PageIndex{4}\)

Prediga la geometría del par de electrones y la estructura molecular de las moléculas de XeF₂.

Respuesta

La geometría del par de electrones es trigonal bipiramidal. La estructura molecular es lineal.

Ejemplo \(\PageIndex{4}\): XeF₄

De todos los gases nobles, el xenón es el más reactivo, reaccionando con frecuencia con elementos como el oxígeno y el flúor. Prediga la geometría del par de electrones y la estructura molecular de la molécula XeF₄.

Solución

La estructura de Lewis de XeF₄ indica seis regiones de alta densidad de electrones alrededor del átomo de xenón: dos pares solitarios y cuatro enlaces:

Figura \(\PageIndex{11}\)). Los cinco átomos están todos en el mismo plano y tienen una estructura molecular plana cuadrada.

Figura \(\PageIndex{11}\): (a)XeF₄ adopta una disposición octaédrica con dos pares solitarios (líneas rojas) y cuatro enlaces en la geometría del par de electrones. (b) La estructura molecular es plana cuadrada con los pares solitarios directamente uno frente al otro.

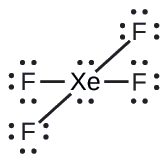
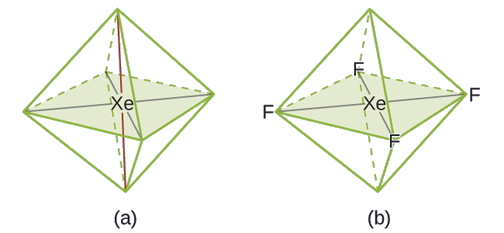
Ejercicio \(\PageIndex{4}\)

En una determinada molécula, el átomo central tiene tres pares solitarios y dos enlaces. ¿Cuál será la geometría del par de electrones y la estructura molecular?

Respuesta

geometría de par de electrones: trigonal bipiramidal; estructura molecular: lineal

Estructura molecular para moléculas multicéntricas

Cuando una molécula o ion poliatómico tiene solo un átomo central, la estructura molecular describe completamente la forma de la molécula. Las moléculas más grandes no tienen un solo átomo central, pero están conectadas por una cadena de átomos interiores que poseen una geometría "local". La forma en que estas estructuras locales están orientadas entre sí también influye en la forma molecular, pero tales consideraciones están fuera del alcance de esta discusión introductoria. Para nuestros propósitos, solo nos enfocaremos en determinar las estructuras locales.

Ejemplo \(\PageIndex{5}\): Predicción de estructura en moléculas multicéntricas

Aquí se muestra la estructura de Lewis para el aminoácido más simple, glicina, H₂NCH₂CO₂H. Prediga la geometría local para el átomo de nitrógeno, los dos átomos de carbono y el átomo de oxígeno con un átomo de hidrógeno unido:

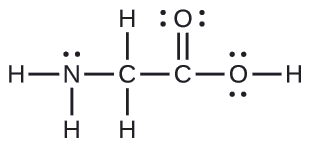
Solución

Considere cada átomo central de forma independiente. Las geometrías de pares de electrones:

• nitrógeno: cuatro regiones de densidad electrónica; tetraédrica
• carbono (CH₂)––cuatro regiones de densidad electrónica; tetraédrica
• carbono (CO₂)—tres regiones de densidad electrónica; plano trigonal
• oxígeno (OH)—cuatro regiones de densidad electrónica; tetraédrica

Las estructuras locales:

• nitrógeno––tres enlaces, un par solitario; piramidal trigonal
• carbono (CH₂)—cuatro enlaces, sin pares solitarios; tetraédrica
• carbono (CO₂)—tres enlaces (el doble enlace cuenta como un enlace), no hay pares solitarios; plano trigonal
• oxígeno (OH)—dos enlaces, dos pares solitarios; angular (109°)

Ejercicio \(\PageIndex{5}\)

Otro aminoácido es la alanina, que tiene la estructura de Lewis que se muestra aquí. Prediga la geometría del par de electrones y la estructura local del átomo de nitrógeno, los tres átomos de carbono y el átomo de oxígeno con hidrógeno unido:

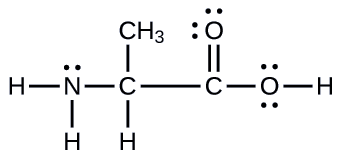
Respuesta

geometrías de pares de electrones: nitrógeno –– tetraédrico; carbono (CH) -tetraédrico; carbono (CH₃) -tetraédrico; carbono (CO₂): plano trigonal; oxígeno (OH) -tetraédrico; estructuras locales: piramidal de nitrógeno trigonal; carbono (CH) -tetraédrico; carbono (CH₃) -tetraédrico; carbono (CO₂): plano trigonal; oxígeno (OH) angular (109 °)

Ejemplo \(\PageIndex{6}\): Simulación Molecular

Usando este simulador de forma molecular nos permite verificar si los ángulos de enlace y / o los pares solitarios se muestran al marcar o desmarcar las casillas debajo de "Opciones" a la derecha. También podemos usar las casillas de verificación "Nombre" en la parte inferior izquierda para mostrar u ocultar la geometría del par de electrones (llamada "geometría de electrones" en el simulador) y / o la estructura molecular (llamada "forma molecular" en el simulador).

Construya la molécula HCN en el simulador basándose en la siguiente estructura de Lewis:

\(\mathrm{H–C≡N}\)

Haga clic en cada tipo de enlace o par solitario a la derecha para agregar ese grupo al átomo central. Una vez que tenga la molécula completa, gírela para examinar la estructura molecular pronosticada. ¿Qué estructura molecular es esta?

Solución

La estructura molecular es lineal.

Ejercicio \(\PageIndex{6}\)

Construya una molécula más compleja en el simulador. Identifique la geometría del grupo de electrones, la estructura molecular y los ángulos de enlace. Luego trate de encontrar una fórmula química que coincida con la estructura que ha dibujado.

Respuesta

Las respuestas variarán. Por ejemplo, un átomo con cuatro enlaces simples, un enlace doble y un par solitario tiene una geometría octaédrica de grupo de electrones y una estructura molecular piramidal cuadrada. XeOF₄ es una molécula que adopta esta estructura.

Polaridad Molecular y Momento Dipolo

Como se discutió anteriormente, los enlaces covalentes polares conectan dos átomos con diferentes electronegatividades, dejando un átomo con una carga positiva parcial (δ +) y el otro átomo con una carga negativa parcial (δ–), a medida que los electrones son atraídos hacia el átomo más electronegativo. Esta separación de carga da lugar a un momento dipolar de enlace. La magnitud de un momento dipolar de enlace está representada por la letra griega mu (µ) y está dada por

\[μ=Qr \label{7.6.X}\]

donde

• \(Q\) es la magnitud de las cargas parciales (determinada por la diferencia de electronegatividad) y
• \(r\) es la distancia entre las cargas

Este momento de enlace se puede representar como un vector, una cantidad que tiene dirección y magnitud (Figura \(\PageIndex{12}\)). Los vectores dipolos se muestran como flechas que apuntan a lo largo del enlace desde el átomo menos electronegativo hacia el átomo más electronegativo. Se dibuja un pequeño signo más en el extremo menos electronegativo para indicar el extremo parcialmente positivo del enlace. La longitud de la flecha es proporcional a la magnitud de la diferencia de electronegatividad entre los dos átomos.

Figura \(\PageIndex{12}\): (a) Hay una pequeña diferencia en la electronegatividad entre C y H, representada como un vector corto. (b) La diferencia de electronegatividad entre B y F es mucho mayor, por lo que el vector que representa el momento del enlace es mucho más largo.

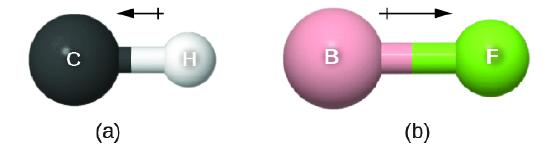
Una molécula completa también puede tener una separación de carga, dependiendo de su estructura molecular y la polaridad de cada uno de sus enlaces. Si existe tal separación de carga, se dice que la molécula es una molécula polar (o dipolo); de lo contrario, se dice que la molécula es no polar. El momento dipolar mide la extensión de la separación de carga neta en toda la molécula. Determinamos el momento dipolar por agregando los momentos de enlace en el espacio tridimensional, teniendo en cuenta la estructura molecular.

Para las moléculas diatómicas, solo hay un enlace, por lo que su momento dipolar de enlace determina la polaridad molecular. Las moléculas diatómicas homonucleares como Br₂ y N₂ no tienen diferencias en la electronegatividad, por eso su momento dipolar es cero. Para las moléculas heteronucleares como el CO, hay un pequeño momento dipolar. Para HF, hay un momento dipolar más grande porque hay una diferencia más grande en la electronegatividad.

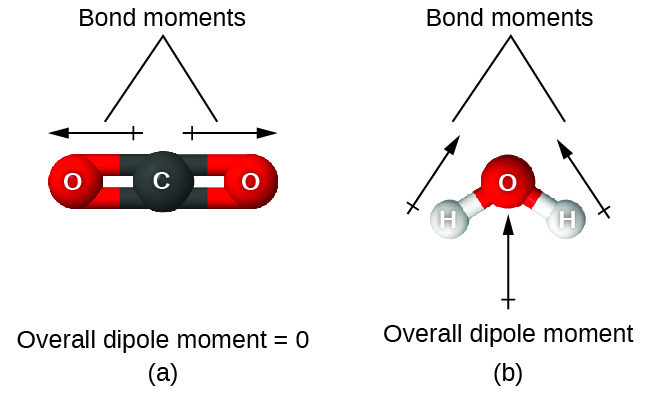
Cuando una molécula contiene más de un enlace, se debe tener en cuenta la geometría. Si los enlaces en una molécula están dispuestos de tal manera que sus momentos de enlace se cancelan (la suma del vector es igual a cero), entonces la molécula es no polar. Esta es la situación en CO₂ (Figura \(\PageIndex{13A}\)). Cada uno de los enlaces es polar, pero la molécula entera es no polar. A partir de la estructura de Lewis y usando la teoría VSEPR, determinamos que la molécula de CO₂ es lineal con enlaces polares C = O en lados opuestos del átomo de carbono. Los momentos de enlace se cancelan porque apuntan en direcciones opuestas. En el caso de la molécula de agua (Figura \(\PageIndex{13B}\)), la estructura de Lewis muestra nuevamente que hay dos enlaces a un átomo central, y la diferencia de electronegatividad muestra nuevamente que cada uno de estos enlaces tiene un enlace distinto de cero momento. Sin embargo, en este caso la estructura molecular es angular debido a los pares solitarios en O, y los dos momentos de enlace no se cancelan. Por lo tanto, el agua tiene un momento dipolar neto y es una molécula polar (dipolo).

Figura \(\PageIndex{13}\): El momento dipolar general de una molécula depende de los momentos dipolares de enlace individuales y de cómo están organizados. (a) Cada enlace de CO tiene un momento dipolar de enlace, pero apuntan en direcciones opuestas para que la molécula neta de CO₂ sea no polar. (b) En contraste, el agua es polar porque los momentos de enlace de OH no se cancelan.

La molécula OCS tiene una estructura similar al CO₂, pero un átomo de azufre ha reemplazado a uno de los átomos de oxígeno. Para determinar si esta molécula es polar, dibujamos la estructura molecular. La teoría VSEPR predice una molécula lineal:

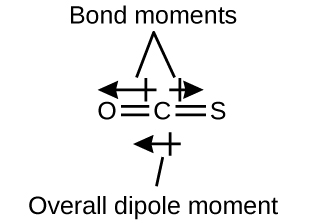
El enlace C - O es significativamente polar. Aunque C y S tienen valores de electronegatividad muy similares, S es un poco más electronegativo que C, por lo que el enlace C-S es un poco polar. Como el oxígeno es más electronegativo que el azufre, el extremo de oxígeno de la molécula es el extremo negativo.

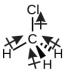
El clorometano, CH₃Cl, es otro ejemplo de una molécula polar. Aunque los enlaces polares C - Cl y C - H están dispuestos en una geometría tetraédrica, los enlaces C - Cl tienen un momento de enlace más grande que el enlace C - H, y los momentos de enlace no se cancelan por completo. Todos los dipolos tienen un componente ascendente en la orientación mostrada, ya que el carbono es más electronegativo que el hidrógeno y menos electronegativo que el cloro:

Cuando examinamos las moléculas altamente simétricas BF₃ (trigonal plana), CH₄ (tetraédrica), PF₅ (trigonal bipiramidal) y SF₆ (octaédrica), en la que todos los enlaces polares son idénticos, las moléculas son no polares. Los enlaces en estas moléculas están dispuestos de tal manera que sus dipolos se cancelan. Sin embargo, el hecho de que una molécula contenga enlaces idénticos no significa que los dipolos siempre se cancelarán. Muchas moléculas que tienen enlaces idénticos y pares solitarios en los átomos centrales tienen dipolos de enlace que no se cancelan. Los ejemplos incluyen H₂S y NH₃. Un átomo de hidrógeno está en el extremo positivo y un átomo de nitrógeno o azufre está en el extremo negativo de los enlaces polares en estas moléculas:

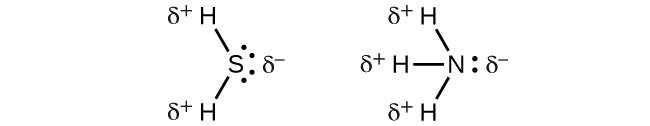
Para resumir, para ser polar, una molécula debe:

1. Contener al menos un enlace covalente polar.
2. Tener una estructura molecular tal que la suma de los vectores de cada momento dipolar de enlace no se cancele.

Propiedades de las moléculas polares

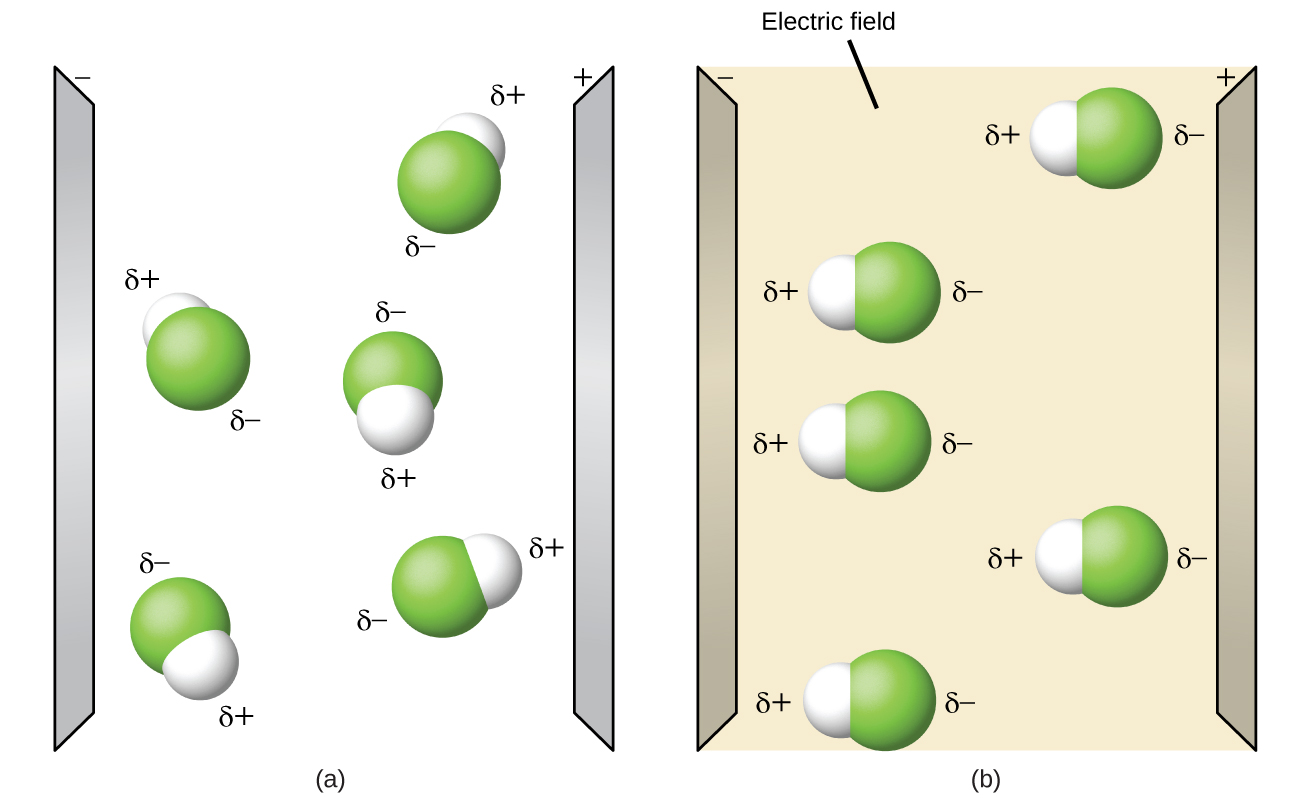
Las moléculas polares tienden a alinearse cuando se colocan en un campo eléctrico con el extremo positivo de la molécula orientado hacia la placa negativa y el extremo negativo hacia la placa positiva (Figura \(\PageIndex{14}\)). Podemos usar un objeto cargado eléctricamente para atraer moléculas polares, pero las moléculas no polares no son atraídas. Además, los solventes polares son mejores para disolver sustancias polares, y los solventes no polares son mejores para disolver sustancias no polares.

Figura \(\PageIndex{14}\): (a) Las moléculas siempre se distribuyen aleatoriamente en estado líquido en ausencia de un campo eléctrico. (b) Cuando se aplica un campo eléctrico, las moléculas polares como HF se alinearán con los dipolos con la dirección del campo.

Ejemplo \(\PageIndex{7}\): Simulaciones de polaridad

Abra la simulación de polaridad de la molécula y seleccione la pestaña "tres átomos" en la parte superior. Esto debería mostrar una molécula ABC con tres ajustadores de electronegatividad. Puede mostrar u ocultar los momentos de enlace, los dipolos moleculares y las cargas parciales a la derecha. Seleccionando el campo eléctrico mostrará si la molécula se mueve cuando se expone a un campo, similar a la Figura \(\PageIndex{14}\).

Use los controles de electronegatividad para determinar cómo se verá el dipolo molecular para la molécula inicial si:

a. A y C son muy electronegativos y B está en el medio del rango.

b. A es muy electronegativo, y B y C no lo son.

Solución

1. El momento dipolar molecular apunta inmediatamente entre A y C.
2. El momento dipolar molecular apunta a lo largo del enlace A - B, hacia A.

Ejercicio \(\PageIndex{7}\)

Determine las cargas parciales que darán los dipolos de enlace más grandes posibles.

Respuesta

Los mayores momentos de enlaces ocurrirán con las mayores cargas parciales. Las dos soluciones anteriores nos enseñan que desigualmente se comparten los electrones en el enlace. Los momentos de enlace se maximizarán cuando la diferencia de electronegatividad sea más grande. Los controles para A y C deben establecerse en un extremo, y B debe establecerse en el extremo opuesto. Aunque la magnitud del momento del enlace no cambiará en función de si B es el más electronegativo o el menos, la dirección del momento del enlace sí lo hará.

Resumen

La teoría de VSEPR predice la disposición tridimensional de los átomos en una molécula. Establece que los electrones de valencia asumirán una geometría de pares de electrones que minimiza las repulsiones entre áreas de alta densidad de electrones (enlaces y/o pares solitarios). La estructura molecular, que se refiere solo a la colocación de átomos en una molécula y no a los electrones, es equivalente a la geometría de pares de electrones solo cuando no hay pares de electrones solitarios alrededor del átomo central. Un momento dipolar mide una separación de carga. Para un enlace, el momento dipolar del enlace está determinado por la diferencia en la electronegatividad entre los dos átomos. Para una molécula, el momento dipolar general está determinado tanto por los momentos de enlace individuales como por la disposición de estos dipolos en la estructura molecular. Las moléculas polares (aquellas con un momento dipolar apreciable) interactúan con los campos eléctricos, mientras que las moléculas no polares no lo hacen.

Glosario

posición axial

ubicación en una geometría bipiramidal trigonal en la que hay otro átomo en un ángulo de 180 ° y las posiciones ecuatoriales están en un ángulo de 90 °

ángulo de enlace

ángulo entre dos enlaces covalentes que comparten un átomo común

distancia de enlace

(también, longitud de enlace) distancia entre los núcleos de dos átomos unidos

momento dipolar de enlace

separación de carga en un enlace que depende de la diferencia en electronegatividad y la distancia de enlace representada por cargas parciales o un vector

momento dipolar

propiedad de una molécula que describe la separación de carga determinada por la suma de los momentos de enlace individuales en función de la estructura molecular

geometría de par de electrones

disposición alrededor de un átomo central de todas las regiones de densidad electrónica (enlaces, pares solitarios o electrones no apareados)

posición ecuatorial

una de las tres posiciones en una geometría bipiramidal trigonal con ángulos de 120 ° entre ellas; las posiciones axiales se ubican en un ángulo de 90 °

lineal

forma en que dos grupos externos se colocan en lados opuestos de un átomo central

estructura molecular

estructura que incluye solo la colocación de los átomos en la molécula

octaédrico

forma en la que se colocan seis grupos externos alrededor de un átomo central de modo que se genera una forma tridimensional con cuatro grupos formando un cuadrado y los otros dos formando el vértice de dos pirámides, una arriba y otra debajo del plano cuadrado

molécula polar

(también, dipolo) molécula con un momento dipolar general

tetraédrica

forma en la que se colocan cuatro grupos externos alrededor de un átomo central de modo que se genera una forma tridimensional con cuatro esquinas y ángulos de 109.5° entre cada par y el átomo central

bipiramidal trigonal

formas en las que cinco grupos externos se colocan alrededor de un átomo central de manera que tres forman un triángulo plano con ángulos de 120 ° entre cada par y el átomo central, y los otros dos forman el vértice de dos pirámides, una arriba y otra debajo del plano triangular

plano trigonal

forma en la que tres grupos externos se colocan en un triángulo plano alrededor de un átomo central con ángulos de 120 ° entre cada par y el átomo central

Teoría de Repulsión de Pares de Electrones de la Valencia (VSEPR)

La teoría utilizada para predecir los ángulos de enlace en una molécula basada en regiones de posicionamiento de alta densidad electrónica lo más separadas posible para minimizar la repulsión electrostática

vector

cantidad que tiene magnitud y dirección

Contribuyentes

Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).