4.8: Uso de Excel y R para analizar datos

Aunque los cálculos de este capítulo son relativamente sencillos, puede resultar tedioso trabajar problemas usando nada más que una calculadora. Tanto Excel como R incluyen funciones para muchos cálculos estadísticos comunes. Además, R proporciona funciones útiles para visualizar tus datos.

Excel

Excel tiene funciones incorporadas que podemos usar para completar muchos de los cálculos estadísticos cubiertos en este capítulo, incluyendo reportar estadísticas descriptivas, como medias y varianzas, predecir la probabilidad de obtener un resultado dado a partir de una distribución binomial o una distribución normal, y realizando pruebas de significancia. Table 4.8.1 proporciona la sintaxis para muchas de estas funciones; puede obtener información sobre las funciones no incluidas aquí usando el menú Ayuda de Excel.

Tabla 4.8.1 : Funciones de Excel para cálculos estadísticos

Parámetro	Función Excel
Estadística Descriptiva
media	= promedio (datos)
mediana	= mediana (datos)
desviación estándar para la muestra	= stdev.s (datos)
desviación estándar para poblaciones	= stdev.p (datos)
varianza para la muestra	= var.s (datos)
varianza para la población	= var.p (datos)
valor máximo	= max (datos)
valor mínimo	= min (datos)
Distribuciones de probabilidad
distribución binomial	= binom.dist (X, N, p, VERDADERO o FALSO)
distribución normal	= norm.dist (x,\(\mu\)\(\sigma\), VERDADERO o FALSO)
Pruebas de significancia
Prueba F	= f.test (conjunto de datos 1, conjunto de datos 2)
t -prueba	= t.test (conjunto de datos 1, conjunto de datos 2, colas = 1 o 2, tipo de t-test: 1 = emparejado; 2 = desemparejado con varianzas iguales; o 3 = desemparejado con varianzas desiguales)

Estadística Descriptiva

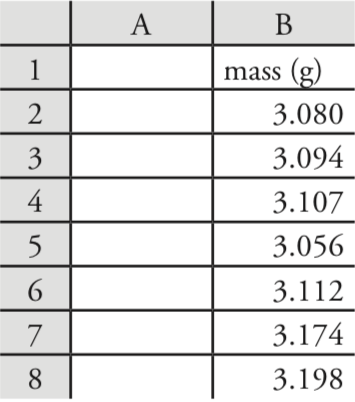
Usemos Excel para proporcionar un resumen estadístico de los datos en la Tabla 4.1.1. Ingresa los datos en una hoja de cálculo, como se muestra en la Figura 4.8.1 . Para calcular la media de la muestra, por ejemplo, haga clic en cualquier celda vacía, ingrese la fórmula

= promedio (b2:b8)

y presione Retorno o Entrar para reemplazar el contenido de la celda con el cálculo de Excel de la media (3.117285714), que redondeamos a 3.117. Excel no tiene una función para el rango, pero podemos usar las funciones que reportan el valor máximo y el valor mínimo para calcular el rango; así

= max (b2:b8) — min (b2:b8)

devuelve 0.142 como respuesta.

Figura 4.8.1 : Porción de una hoja de cálculo que contiene datos de la Tabla 4.1.1.

Distribuciones de probabilidad

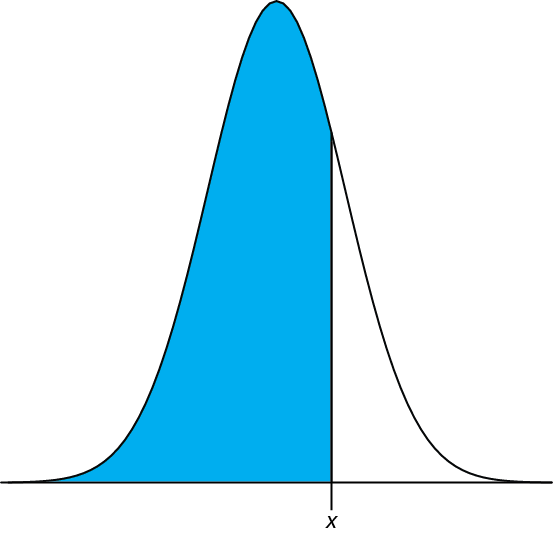
En el Ejemplo 4.4.2 se demostró que 91.10% de las tabletas analgésicas de un fabricante contenían entre 243 y 262 mg de aspirina. Llegamos a este resultado calculando la desviación, z, de cada límite de la media esperada de la población\(\mu\), de 250 mg en términos de la desviación estándar esperada de la población\(\sigma\),, de 5 mg. Después de calcular los valores para z, utilizamos la tabla del Apéndice 3 para encontrar el área bajo la curva de distribución normal entre estos dos límites.

Podemos completar este cálculo en Excel usando la función norm.dist Como se muestra en la Figura 4.8.2 , la función calcula la probabilidad de obtener un resultado menor que x a partir de una distribución normal con una media de\(\mu\) y una desviación estándar de\(\sigma\). Para resolver Ejemplo 4.4.2 usando Excel ingrese las siguientes fórmulas en celdas separadas

= norm.dist (243, 250, 5, VERDADERO)

= norm.dist (262, 250, 5, VERDADERO)

obteniendo resultados de 0.080756659 y 0.991802464. Restar el valor menor del valor mayor y ajustar al número correcto de cifras significativas da la probabilidad como 0.9910, o 99.10%.

Figura 4.8.2 : Se muestra en azul el área devuelta por la función norm.dist (x,\(\mu\)\(\sigma\), TRUE). El último parámetro, verdadero, devuelve la distribución acumulativa de\(- \infty \text{ to } x\); al ingresar FALSE se obtiene la probabilidad de obtener un resultado mayor que x. Para nuestros propósitos, queremos usar VERDADERO.

Excel también incluye una función para trabajar con distribuciones binomiales. La sintaxis de la función es

= binom.dist (X, N, p, VERDADERO o FALSO)

donde X es el número de veces que ocurre un resultado particular en N ensayos, y p es la probabilidad de que X ocurra en un solo ensayo. Establecer el último término de la función en VERDADERO da la probabilidad total para cualquier resultado hasta X y establecerlo en FALSE da la probabilidad para X. Usando el Ejemplo 4.4.1 para probar esta función, usamos la fórmula

= binom.dist (0, 27, 0.0111, FALSO)

para encontrar la probabilidad de no encontrar átomos de ¹³ átomos de C en una molécula de colesterol, C ₂₇ H ₄₄ O, que devuelve un valor de 0.740 después de ajustar por cifras significativas. Usando la fórmula

= binom.dist (2, 27, 0.0111, VERDADERO)

encontramos que 99.7% de las moléculas de colesterol contienen dos o menos átomos de ¹³ C.

Pruebas de significancia

Como se muestra en la Tabla 4.8.1 , Excel incluye funciones para las siguientes pruebas de significación cubiertas en este capítulo:

• una prueba F de varianzas
• una prueba t desapareada de medias de muestra asumiendo varianzas iguales
• una prueba t desapareada de medias de muestra asumiendo varianzas desiguales
• una prueba t pareada para de medias de muestra

Usemos estas funciones para completar una prueba t sobre los datos del Cuadro 4.4.1, que contiene los resultados de dos experimentos para determinar la masa de un penique circulante de Estados Unidos. Ingrese los datos de la Tabla 4.4.1 en una hoja de cálculo como se muestra en la Figura 4.8.3 .

Figura 4.8.3 : Porción de una hoja de cálculo que contiene los datos de la Tabla 4.4.1.

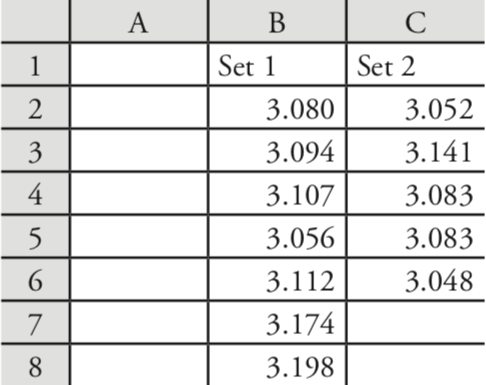
Debido a que los datos en este caso no están emparejados, usaremos Excel para completar una prueba t desemparejada. Antes de que podamos completar la prueba t, usamos una prueba F para determinar si las varianzas para los dos conjuntos de datos son iguales o desiguales.

Para completar la prueba F, damos clic en cualquier celda vacía, ingresamos la fórmula

= f.test (b2:b8, c2:c6)

y presione Retorno o Enter, que reemplaza el contenido de la celda con el valor de\(\alpha\) para el cual podemos rechazar la hipótesis nula de varianzas iguales. En este caso, Excel devuelve una\(\alpha\) de 0.566 105 03; debido a que este valor no es menor a 0.05, conservamos la hipótesis nula de que las varianzas son iguales. La prueba F de Excel es de dos colas; para una prueba F de una cola, usamos la misma función, pero dividimos el resultado por dos; así

= f.test (b2:b8, c2:c6) /2

Al no haber encontrado evidencia que sugiera varianzas desiguales, luego completamos una prueba t desapareada asumiendo varianzas iguales, ingresando en cualquier celda vacía la fórmula

= t.test (b2:b8, c2:c6, 2, 2)

donde el primero 2 indica que se trata de una prueba t de dos colas, y el segundo 2 indica que se trata de una prueba t desapareada con varianzas iguales. Al presionar Return o Enter se reemplaza el contenido de la celda con el valor de\(\alpha\) para el cual podemos rechazar la hipótesis nula de medias iguales. En este caso, Excel devuelve una\(\alpha\) de 0.211 627 646; debido a que este valor no es menor a 0.05, conservamos la hipótesis nula de que las medias son iguales.

Consulte el Ejemplo 4.6.3 y el Ejemplo 4.6.4 para conocer nuestras soluciones anteriores a este problema.

Las otras pruebas de significancia en Excel funcionan en el mismo formato. El siguiente ejercicio de práctica te brinda la oportunidad de ponerte a prueba.

Ejercicio 4.8.1

Retrabajo Ejemplo 4.6.5 y Ejemplo 4.6.6 usando Excel.

Contestar

Encontrará pequeñas diferencias entre los valores que obtiene utilizando las funciones integradas de Excel y las soluciones trabajadas en el capítulo. Estas diferencias surgen porque Excel no redondea los resultados de los cálculos intermedios.

R

R es un entorno de programación que proporciona potentes capacidades para analizar datos. Hay muchas funciones integradas en la instalación estándar de R y paquetes adicionales de funciones están disponibles en el sitio web de R (www.r-project.org). Los comandos en R no están disponibles en los menús desplegables. En cambio, interactúas con R escribiendo comandos.

Puede descargar la versión actual de R desde www.r-project.org. Haga clic en el enlace para Descargar: CRAN y encuentre un sitio espejo local. Haga clic en el enlace del sitio espejo y luego use el enlace para Linux, macOS X o Windows bajo el encabezado “Descargar e instalar R.”

Estadística Descriptiva

Usemos R para proporcionar un resumen estadístico de los datos en la Tabla 4.1.1. Para ello primero necesitamos crear un objeto que contenga los datos, lo cual hacemos escribiendo el siguiente comando.

> penny1 = c (3.080, 3.094, 3.107, 3.056, 3.112, 3.174, 3.198)

En R, el símbolo '>' es un prompt, lo que indica que el programa está esperando que ingreses un comando. Cuando presiona 'Retorno' o 'Intro, 'R ejecuta el comando, muestra el resultado (si hay un resultado que devolver) y devuelve el símbolo >.

Table 4.8.2 enumera algunos de los comandos en R para calcular estadísticas descriptivas básicas. Como es el caso de Excel, R no incluye comandos independientes para todas las estadísticas descriptivas de interés para nosotros, pero podemos calcularlas usando otros comandos. Usar un comando es fácil: simplemente ingrese el código apropiado en la solicitud; por ejemplo, para encontrar la varianza de la muestra ingresamos

> var (penny1)

[1] 0.002221918

Tabla 4.8.2 : Funciones R para estadística descriptiva

Parámetro	Función Excel
media	mean (objeto)
mediana	median (objeto)
desviación estándar para la muestra	sd (objeto)
desviación estándar para poblaciones	sd (objeto) * ((longitud (objeto) — 1) /longitud (objeto)) ^0.5
varianza para la muestra	var (objeto)
varianza para la población	var (objeto) * ((longitud (objeto) — 1) /longitud (objeto))
gama	max (objeto) — min (objeto)

Distribuciones de probabilidad

En el Ejemplo 4.4.2 se demostró que 91.10% de las tabletas analgésicas de un fabricante contenían entre 243 y 262 mg de aspirina. Llegamos a este resultado calculando la desviación, z, de cada límite de la media esperada de la población\(\mu\), de 250 mg en términos de la desviación estándar esperada de la población\(\sigma\),, de 5 mg. Después de calcular los valores para z, utilizamos la tabla del Apéndice 3 para encontrar el área bajo la curva de distribución normal entre estos dos límites.

Podemos completar este cálculo en R usando la función pnorm. El formato general de la función es

pnorm (\(x, \mu, \sigma\))

donde x es el límite de interés,\(\mu\) es la media esperada de la distribución y\(\sigma\) es la desviación estándar esperada de la distribución. La función devuelve la probabilidad de obtener un resultado menor que x (Figura 4.8.4 ).

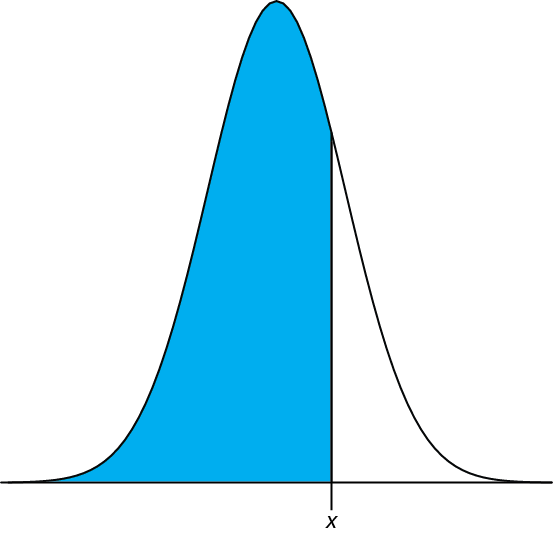
Figura 4.8.4 : Se muestra en azul el área devuelta por la función pnorm (\(x, \mu, \sigma\)).

Aquí está el resultado de una sesión R para resolver Ejemplo 4.4.2.

> pnorm (243, 250, 5)

[1] 0.08075666

> pnorm (262, 250, 5)

[1] 0.9918025

Restar el valor menor del valor mayor y ajustar al número correcto de cifras significativas da la probabilidad como 0.9910, o 99.10%.

R también incluye funciones para distribuciones binomiales. Para encontrar la probabilidad de obtener un resultado particular, X, en N ensayos utilizamos la función dbinom.

dbinom (X, N, p)

donde X es el número de veces que ocurre un resultado particular en N ensayos, y p es la probabilidad de que X ocurra en un solo ensayo. Usando el Ejemplo 4.4.1 para probar esta función, encontramos que la probabilidad de no encontrar átomos de ¹³ átomos de C en una molécula de colesterol, C ₂₇ H ₄₄ O es

> dbinom (0, 27, 0.0111)

[1] 0.7397997

0.740 después de ajustar las cifras significativas. Para encontrar la probabilidad de obtener algún resultado hasta un valor máximo de X, utilizamos la función pbinom.

pbinom (X, N, p)

Para encontrar el porcentaje de moléculas de colesterol que contienen 0, 1 o 2 átomos de ¹³ C, ingresamos

> pbinom (2, 27, 0.0111)

[1] 0.9967226

y encontrar que la respuesta es 99.7% de las moléculas de colesterol.

Pruebas de significancia

R incluye comandos para las siguientes pruebas de significación cubiertas en este capítulo:

• F -prueba de varianzas
• prueba t desapareada de medias de muestra asumiendo varianzas iguales
• prueba t desapareada de medias de muestra asumiendo varianzas desiguales
• prueba t pareada para de medias de muestra
• Prueba Q de Dixon para valores atípicos
• Prueba de Grubb para valores atípicos

Usemos estas funciones para completar una prueba t sobre los datos del Cuadro 4.4.1, que contiene los resultados de dos experimentos para determinar la masa de un penique circulante de Estados Unidos. Primero, ingrese los datos de la Tabla 4.4.1 en dos objetos.

> penny1 = c (3.080, 3.094, 3.107, 3.056, 3.112, 3.174, 3.198)

> penny2 = c (3.052, 3.141, 3.083, 3.083, 3.048)

Debido a que los datos en este caso no están emparejados, usaremos R para completar una prueba t desapareada. Antes de que podamos completar una prueba t utilizamos una prueba F para determinar si las varianzas para los dos conjuntos de datos son iguales o desiguales.

Para completar una prueba F de dos colas en R usamos el comando

var.test (X, Y)

donde X e Y son los objetos que contienen los dos conjuntos de datos. La figura 4.8.5 muestra la salida de una sesión R para resolver este problema.

Figura 4.8.5 : Salida de una sesión R para una prueba F de varianzas. El valor p de 0.5661 es la probabilidad de rechazar incorrectamente la hipótesis nula de que las varianzas son iguales (nota: R identifica\(\alpha\) como un valor p). El intervalo de confianza del 95% es el rango de valores para F _exp que se explican por error aleatorio. Si este rango incluye el valor esperado para F, en este caso 1.00, entonces no hay evidencia suficiente para rechazar la hipótesis nula. Tenga en cuenta que R no ajusta para cifras significativas.

Tenga en cuenta que R no proporciona el valor crítico para F (0.05, 6, 4); en cambio, reporta el intervalo de confianza del 95% para F _exp. Debido a que este intervalo de confianza de 0.204 a 11.661 incluye el valor esperado para F de 1.00, conservamos la hipótesis nula y no tenemos evidencia de diferencia entre las varianzas. R también proporciona la probabilidad de rechazar incorrectamente la hipótesis nula, que en este caso es 0.5561.

Para una prueba F de una cola, el comando es uno de los siguientes

var.test (X, Y, alternativa = “mayor”)

var.test (X, Y, alternativa = “menos”)

donde se usa “mayor” cuando la hipótesis alternativa es\(s_X^2 > s_Y^2\), y “menos” cuando la hipótesis alternativa es\(s_X^2 < s_Y^2\).

Al no haber encontrado evidencia que sugiera varianzas desiguales, ahora completamos una prueba t desapareada asumiendo varianzas iguales. La sintaxis básica para una prueba t de dos colas es

t.test (X, Y, mu = 0, emparejado = FALSO, var.igual = FALSO)

donde X e Y son los objetos que contienen los conjuntos de datos. Se pueden cambiar los términos subrayados para alterar la naturaleza de la prueba t. Reemplazar “var.equal = FALSO” por “var.equal = VERDADERO” hace que esta sea una prueba t de dos colas con varianzas iguales, y reemplazar “emparejado = FALSO” por “emparejado = VERDADERO” hace que esta sea una prueba t pareada. El término “mu = 0” es la diferencia esperada entre las medias, que para este problema es 0. Puedes, por supuesto, cambiar esto para adaptarlo a tus necesidades. Los términos subrayados son valores predeterminados; si los omite, entonces R asume que pretende una prueba t de dos colas desemparejada de la hipótesis nula de que X = Y con varianzas desiguales. La figura 4.8.6 muestra la salida de una sesión R para este problema.

Figura 4.8.6 : Salida de una sesión R para una prueba t desemparejada con varianzas iguales. El valor p de 0.2116 es la probabilidad de rechazar incorrectamente la hipótesis nula de que las medias son iguales (nota: R identifica\(\alpha\) como un valor p). El intervalo de confianza del 95% es el rango de valores para la diferencia entre las medias que se explica por error aleatorio. Si este rango incluye el valor esperado para la diferencia, en este caso cero, entonces no hay evidencia suficiente para rechazar la hipótesis nula. Tenga en cuenta que R no ajusta para cifras significativas.

Podemos interpretar los resultados de esta prueba t de dos maneras. Primero, el valor p de 0.2116 significa que hay un 21.16% de probabilidad de rechazar incorrectamente la hipótesis nula. Segundo, el intervalo de confianza del 95% de —0.024 a 0.0958 para la diferencia entre las medias de la muestra incluye el valor esperado de cero. Ambas formas de ver los resultados no proporcionan evidencia para rechazar la hipótesis nula; así, conservamos la hipótesis nula y no encontramos evidencia de diferencia entre las dos muestras.

Las otras pruebas de significancia en R funcionan en el mismo formato. El siguiente ejercicio de práctica te brinda la oportunidad de ponerte a prueba.

Ejercicio 4.8.2

Retrabajo Ejemplo 4.6.5 y Ejemplo 4.6.6 usando R.

Responder

Aquí se muestran copias de R sesiones para cada problema. Encontrará pequeñas diferencias entre los valores dados aquí para t _exp y para F _exp y aquellos valores mostrados con las soluciones trabajadas en el capítulo. Estas diferencias surgen porque R no redondea los resultados de los cálculos intermedios.

Ejemplo 4.6.5

> Analista= c (86.82, 87.04, 86.93, 87.01, 86.20, 87.00)

> AnalistaB = c (81.01, 86.15, 81.73, 83.19, 80.27, 83.94)

> var.test (AnalystB, AnalystA)

Prueba F para comparar dos varianzas

datos: AnalystB y AnalystA

F = 45.6358, num df = 5, denom df = 5, valor p = 0.0007148

hipótesis alternativa: la relación verdadera de varianzas no es igual a 1

Intervalo de confianza del 95 por ciento:

6.385863 326.130970

estimaciones de la muestra:

relación de varianzas

45.63582

> t.test (AnalystA, AnalystB, var.equal=false)

Prueba t de dos muestras Welch

datos: Analysta y AnalystB

t = 4.6147, df = 5.219, valor p = 0.005177

hipótesis alternativa: la verdadera diferencia en medias no es igual a 0

Intervalo de confianza del 95 por ciento: 1.852919 6.383748

estimaciones muestrales: media de x media de y

86.83333 82.71500

Ejemplo 4.21

> micro = c (129.5, 89.6, 76.6, 52.2, 110.8, 50.4, 72.4, 141.4, 75.0, 34.1, 60.3)
> elect = c (132.3, 91.0, 73.6, 58.2, 104.2, 49.9, 82.1, 154.1, 73.4, 38.1, 60.1)

> t.test (micro, electos, paired=true)

Prueba t pareada

datos: micro y elect

t = -1.3225, df = 10, valor p = 0.2155

hipótesis alternativa: la verdadera diferencia en medias no es igual a 0

Intervalo de confianza del 95 por ciento:

-6.028684 1.537775

estimaciones de la muestra:

media de las diferencias

—2.245455

A diferencia de Excel, R también incluye funciones para evaluar valores atípicos. Estas funciones no forman parte de la instalación estándar de R. Para instalarlos ingresa el siguiente comando dentro de R (nota: necesitarás una conexión a internet para descargar el paquete de funciones).

> install.packages (“valores atípicos”)

Después de instalar el paquete, debe cargar las funciones en R usando el siguiente comando (nota: debe realizar este paso cada vez que comience una nueva sesión R ya que el paquete no se carga automáticamente cuando inicia R).

> biblioteca (“valores atípicos”)

Necesitas instalar un paquete una vez, pero debes cargarlo cada vez que planeas usarlo. Hay formas de configurar R para que cargue automáticamente ciertos paquetes; consulte Una introducción a R para obtener más información (haga clic aquí para ver una versión PDF de este documento).

Usemos este paquete para encontrar el valor atípico en la Tabla 4.6.1 usando tanto la prueba Q de Dixon como la prueba de Grubb. Los comandos para estas pruebas son

dixon.test (X, tipo = 10, dos.sided = VERDADERO)

grubbs.test (X, tipo = 10, dos.caras = VERDADERO)

donde X es el objeto que contiene los datos, “type = 10” especifica que estamos buscando un valor atípico, y “two.sided = TRUE” indica que estamos usando la prueba de dos colas más conservadora. Ambas pruebas tienen otras variantes que permiten la prueba de valores atípicos en ambos extremos del conjunto de datos (“type = 11”) o para más de un valor atípico (“type = 20”), pero no las consideraremos aquí. La figura 4.8.7 muestra la salida de una sesión para este problema. Para ambas pruebas el valor p muy pequeño indica que podemos tratar como un valor atípico el centavo con una masa de 2.514 g.

Figura 4.8.7 : Salida de una sesión R para la prueba Q de Dixon y la prueba de Grubb para valores atípicos. Los valores p para ambas pruebas muestran que podemos tratar como un valor atípico el centavo con una masa de 2.514 g.

Visualización de datos

Una de las características más útiles de R es la capacidad de visualizar datos. Visualizar datos es importante porque nos proporciona una sensación intuitiva de nuestros datos que nos puede ayudar en la aplicación y evaluación de pruebas estadísticas. Es tentador creer que un análisis estadístico es infalible, particularmente si la probabilidad de rechazar incorrectamente la hipótesis nula es pequeña. Sin embargo, observar una visualización visual de nuestros datos puede ayudarnos a determinar si nuestros datos están normalmente distribuidos, un requisito para la mayoría de las pruebas de significancia de este capítulo, y puede ayudarnos a identificar posibles valores atípicos. Existen muchas formas útiles de ver los datos, cuatro de las cuales consideramos aquí.

Visualizar datos es importante, punto al que volveremos en el Capítulo 5 cuando consideremos el modelado matemático de los datos.

Para trazar datos en R, usaremos el paquete “celosía”, que necesitarás cargar usando el siguiente comando.

> biblioteca (“celosía”)

Para demostrar los tipos de parcelas que podemos generar, utilizaremos el objeto “penny”, que contiene las masas de los 100 peniques en la Tabla 4.4.3.

No es necesario usar el comando install.package esta vez porque la celosía se instaló automáticamente en su computadora cuando descargó R.

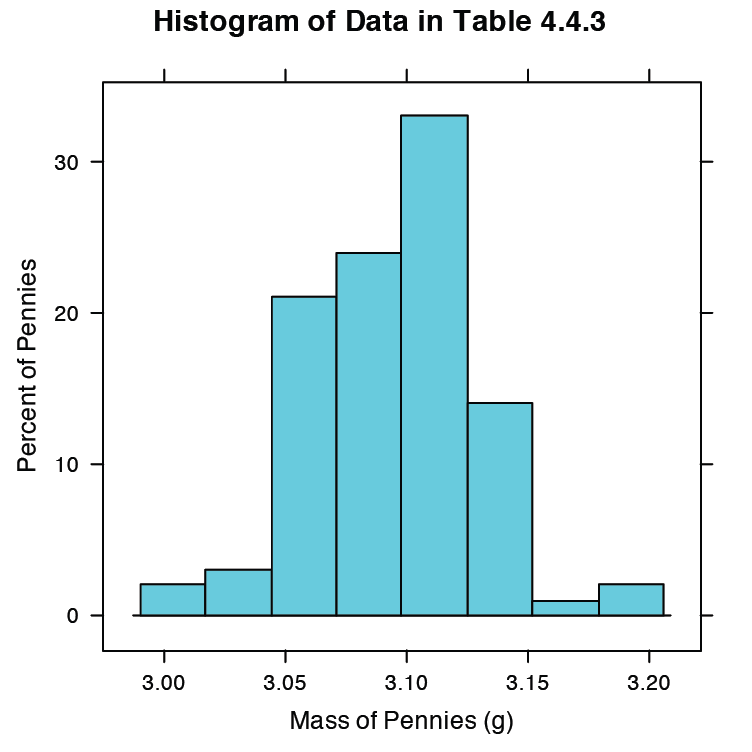
Nuestra primera visualización es un histograma. Para construir el histograma usamos masa para dividir los centavos en bins y trazar el número de centavos o el porcentaje de centavos en cada bin en el eje y como una función de la masa en el eje x. La figura 4.8.8 muestra el resultado de ingresar el comando

> histograma (centavo, tipo = “por ciento”, xlab = “Masa (g)”, ylab = “Porcentaje de centavos”, main = “Histograma de Datos en la Tabla 4.4.3”)

Un histograma nos permite visualizar la distribución de los datos. En este ejemplo los datos parecen seguir una distribución normal, aunque el bin más grande no incluye la media de 3.095 g y la distribución no es perfectamente simétrica. Una limitación de un histograma es que su apariencia depende de cómo elegimos clasificar los datos. Aumentar el número de bins y centrar los bins alrededor de la media de los datos da un histograma que se aproxima más a una distribución normal (Figura 4.4.5).

Figura 4.8.8 : Histograma de los datos de la Tabla 4.4.3.

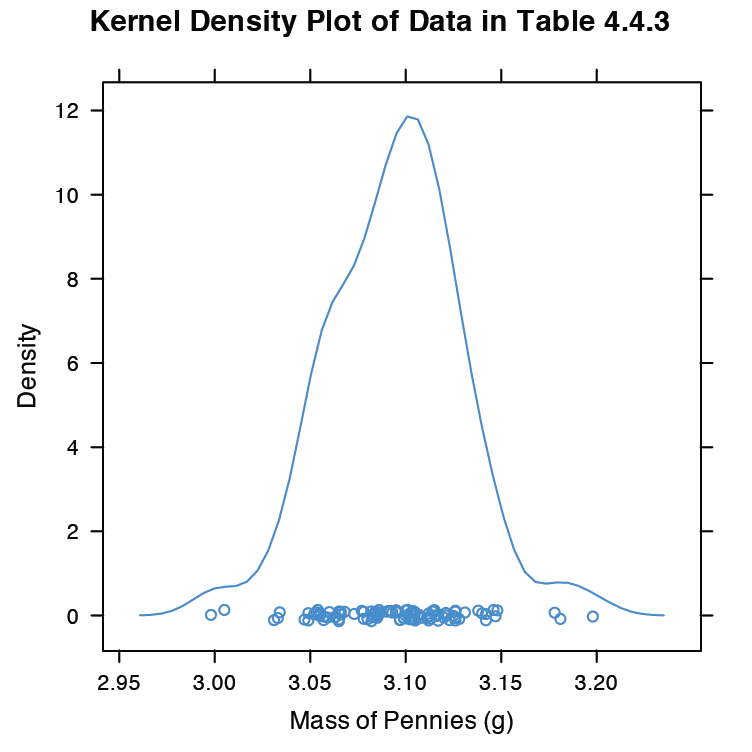
Una alternativa al histograma es una gráfica de densidad de kernel, que básicamente es un histograma suavizado. En esta gráfica cada valor del conjunto de datos es reemplazado por una curva de distribución normal cuyo ancho es una función de la desviación estándar y tamaño del conjunto de datos. La curva resultante es una suma de las distribuciones individuales. La figura 4.8.9 muestra el resultado de ingresar el comando

> densityplot (penny, xlab = “Masa de Centavos (g)”, main = “Gráfica de Densidad de Núcleo de Datos en la Tabla 4.4.3”)

Los círculos en la parte inferior de la trama muestran la masa de cada centavo en el conjunto de datos. Esta visualización proporciona una imagen más convincente de que los datos del Cuadro 4.4.3 se distribuyen normalmente, aunque vemos evidencia de un pequeño agrupamiento de centavos con una masa de aproximadamente 3.06 g.

Figura 4.8.9 : Gráfica Kernal de los datos de la Tabla 4.4.3.

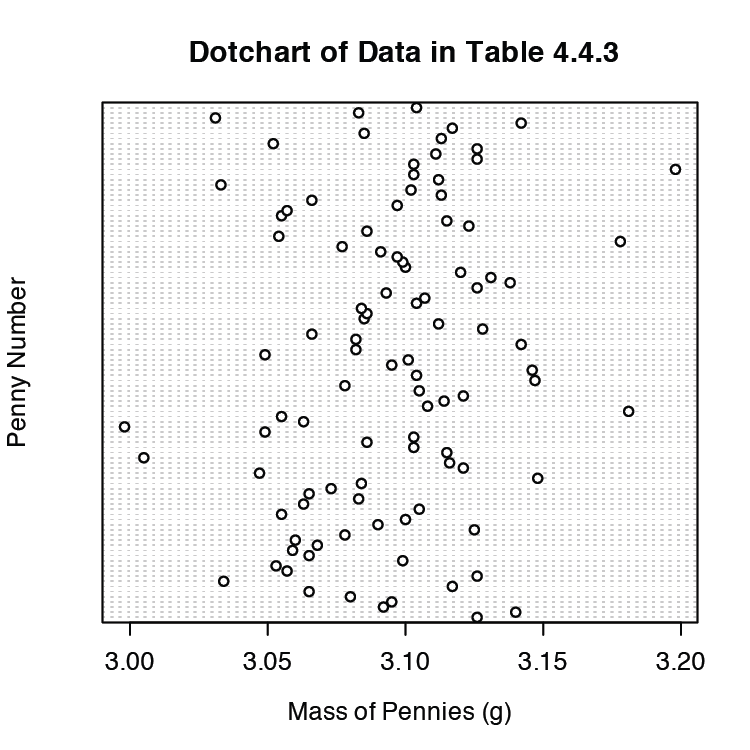
Analizamos muestras para caracterizar la población parental. Para llegar a una conclusión significativa sobre una población, las muestras deben ser representativas de la población. Un requisito importante es que las muestras sean aleatorias. Un gráfico de puntos proporciona una visualización visual simple que nos permite examinar los datos para detectar tendencias no aleatorias. La figura 4.8.10 muestra el resultado de ingresar

> dotchart (penny, xlab = “Masa de centavos (g)”, ylab = “Número de centavo”, main = “Gráfico de puntos de datos en la Tabla 4.4.3”)

En esta parcela las masas de los 100 centavos se disponen a lo largo del eje y en el orden en que fueron muestreadas. Si vemos un patrón en los datos a lo largo del eje y, como una tendencia hacia masas más pequeñas a medida que pasamos del primer centavo al último centavo, entonces tenemos evidencia clara de muestreo no aleatorio. Debido a que nuestros datos no muestran un patrón, tenemos más confianza en la calidad de nuestros datos.

Figura 4.8.10 : Gráfico de puntos de los datos de la Tabla 4.4.3. Tenga en cuenta que la dispersión de puntos a lo largo del eje x no es uniforme, con más puntos que ocurren cerca del centro del eje x que en cualquiera de los extremos. Este patrón es el esperado para una distribución normal.

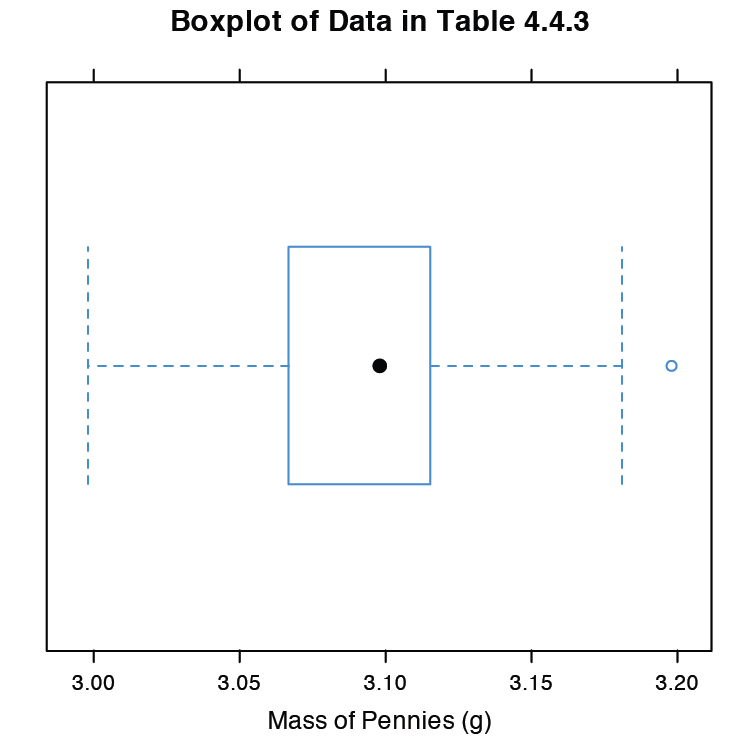
La última gráfica que consideraremos es una gráfica de caja, que es una forma útil de identificar posibles valores atípicos sin hacer suposiciones sobre la distribución de los datos. Una gráfica de caja contiene cuatro piezas de información sobre un conjunto de datos: la mediana, el 50% medio de los datos, el valor más pequeño y el valor más grande dentro de una distancia establecida del 50% medio de los datos, y posibles valores atípicos. La figura 4.8.11 muestra el resultado de ingresar

> bwplot (penny, xlab = “Masa de centavos (g)”, main = “Gráfica de caja de datos en la Tabla 4.4.3)”

El punto negro (•) es la mediana del conjunto de datos. La caja rectangular muestra el rango de masas que abarca el 50% medio de los centavos. Esto también se conoce como el rango intercuartílico, o IQR. Las líneas discontinuas, que se llaman “bigotes”, se extienden hasta el valor más pequeño y el valor más grande que se encuentran dentro\(\pm 1.5 \times \text{IQR}\) de la caja rectangular. Los valores atípicos potenciales se muestran como círculos abiertos (o). Para los datos normalmente distribuidos la mediana está cerca del centro de la caja y los bigotes serán equidistantes de la caja. Como suele ocurrir en las estadísticas, lo contrario no es cierto: encontrar que una gráfica de caja es perfectamente simétrica no prueba que los datos se distribuyan normalmente.

Figura 4.8.11 : Gráfica de caja de los datos de la Tabla 4.4.3.

Para encontrar el rango intercuartílico primero se encuentra la mediana, que divide los datos a la mitad. La mediana de cada mitad proporciona los límites para la caja. El IQR es la mediana de la mitad superior de los datos menos la mediana para la mitad inferior de los datos. Para los datos del Cuadro 4.4.3 la mediana es de 3.098. La mediana para la mitad inferior de los datos es 3.068 y la mediana para la mitad superior de los datos es 3.115. El IQR es 3.115 — 3.068 = 0.047. Puedes usar el comando “summary (penny)” en R para obtener estos valores.

Los “bigotes” inferiores se extienden hasta el primer punto de datos con una masa mayor que

3.068 — 1.5\(\times\) IQR = 3.068 — 1.5\(\times\) 0.047 = 2.9975

que para estos datos es de 2.998 g. El “bigote” superior se extiende hasta el último punto de datos con una masa menor que

3.115 + 1.5\(\times\) IQR = 3.115 + 1.5\(\times\) 0.047 = 3.1855

que para estos datos es de 3.181 g.

La gráfica de caja en la Figura 4.8.11 es consistente con el histograma (Figura 4.8.8 ) y la gráfica de densidad del kernel (Figura 4.8.9 ). En conjunto, las tres parcelas proporcionan evidencia de que los datos del Cuadro 4.4.3 se distribuyen normalmente. El valor atípico potencial, cuya masa de 3.198 g, no está lo suficientemente lejos del bigote superior como para ser preocupante, particularmente porque el tamaño del conjunto de datos (n = 100) es tan grande. Una prueba de Grubb sobre el valor atípico potencial no proporciona evidencia para tratarlo como un valor atípico.

Ejercicio 4.8.3

Utilice R para crear un conjunto de datos que consta de 100 valores a partir de una distribución uniforme ingresando el comando

> datos = runif (100, min = 0, max = 100)

Una distribución uniforme es aquella en la que cada valor entre el mínimo y el máximo es igualmente probable. Examine el conjunto de datos creando un histograma, una gráfica de densidad del núcleo, una gráfica de puntos y una gráfica de caja. Comenta brevemente lo que te dicen las parcelas sobre tu muestra y su población matriz.

Responder

Debido a que estamos seleccionando una muestra aleatoria de 100 miembros de una distribución uniforme, verá diferencias sutiles entre sus parcelas y las gráficas mostradas como parte de esta respuesta. Aquí hay un registro de mi sesión R y las parcelas resultantes.

> datos = runif (100, min = 0, max = 0)

> datos

[1] 18.928795 80.423589 39.399693 23.757624 30.088554

[6] 76.622174 36.487084 62.186771 81.115515 15.726404

[11] 85.765317 53.994179 7.919424 10.125832 93.153308

[16] 38.079322 70.268597 49.879331 73.115203 99.329723

[21] 48.203305 33.093579 73.410984 75.128703 98.682127

[26] 11.433861 53.337359 81.705906 95.444703 96.843476

[31] 68.251721 40.567993 32.761695 74.635385 70.914957

[36] 96.054750 28.448719 88.580214 95.059215 20.316015

[41] 9.828515 44.172774 99.648405 85.593858 82.745774

[46] 54.963426 65.563743 87.820985 17.791443 26.417481

[51] 72.832037 5.518637 58.231329 10.213343 40.581266

[56] 6.584000 81.261052 48.534478 51.830513 17.214508

[61] 31.232099 60.545307 19.197450 60.485374 50.414960

[66] 88.908862 68.939084 92.515781 72.414388 83.195206

[71] 74.783176 10.643619 41.775788 20.464247 14.547841

[76] 89.887518 56.217573 77.606742 26.956787 29.641171

[81] 97.624246 46.406271 15.906540 23.007485 17.715668

[86] 84.652814 29.379712 4.093279 46.213753 57.963604

[91] 91.160366 34.278918 88.352789 93.004412 31.055807

[96] 47.822329 24.052306 95.498610 21.089686 2.629948

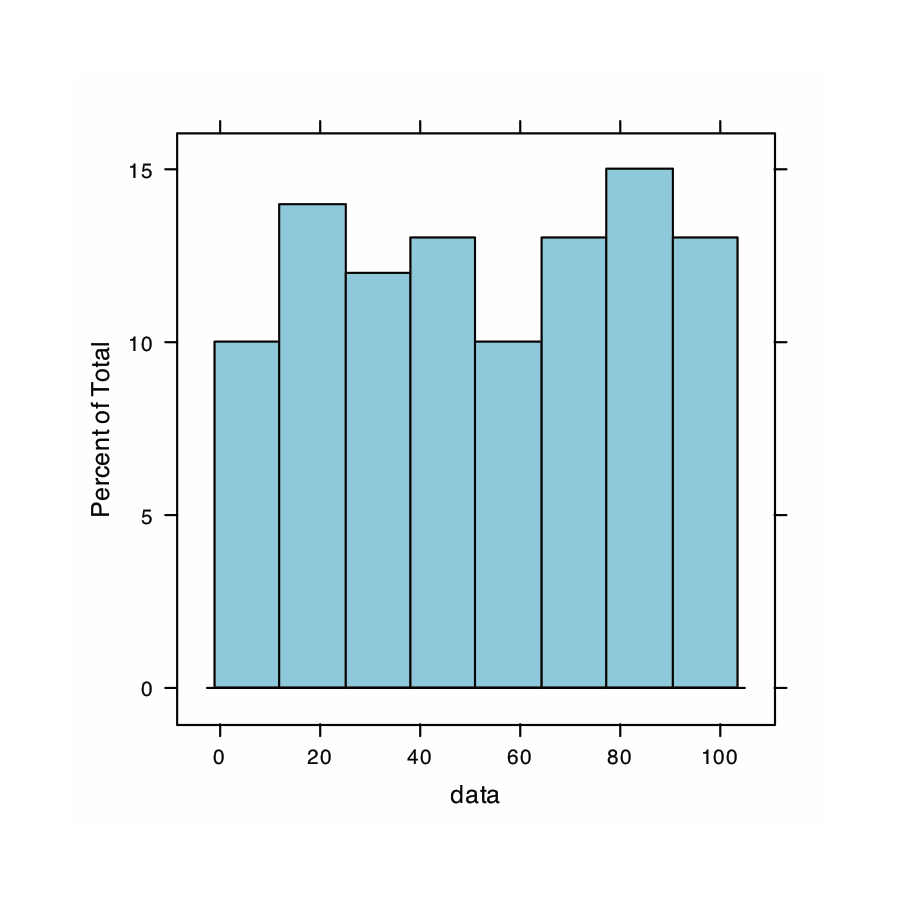
> histograma (datos, tipo = “por ciento”)

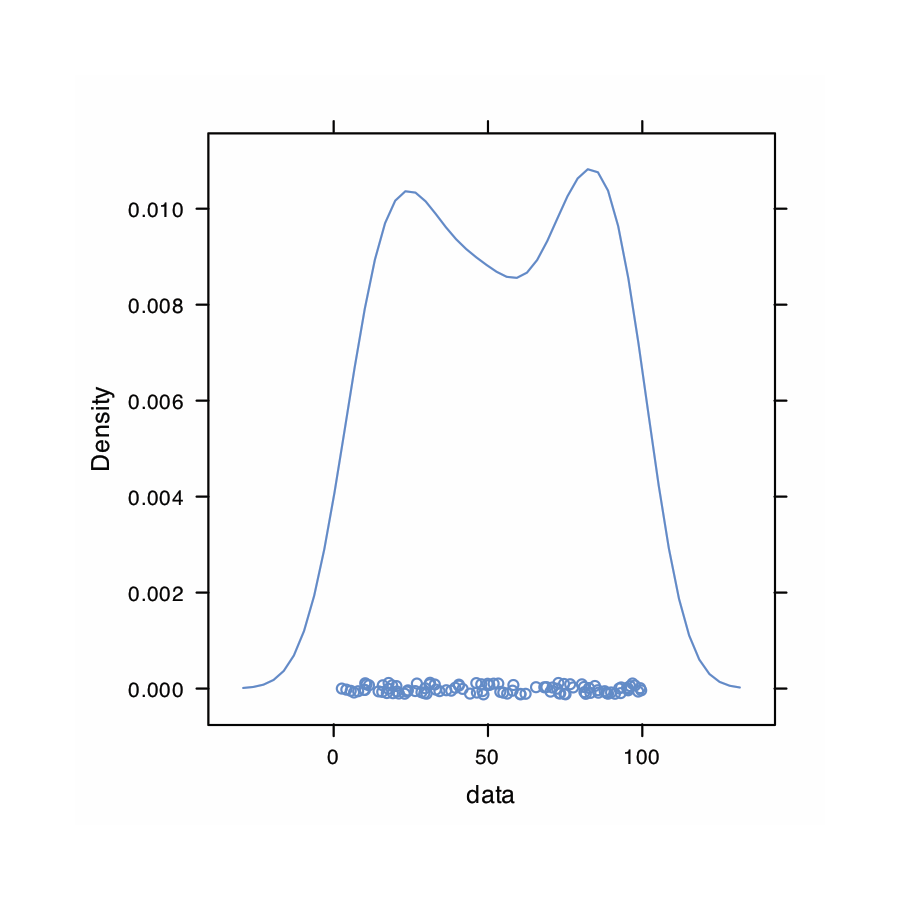
> densityplot (datos)

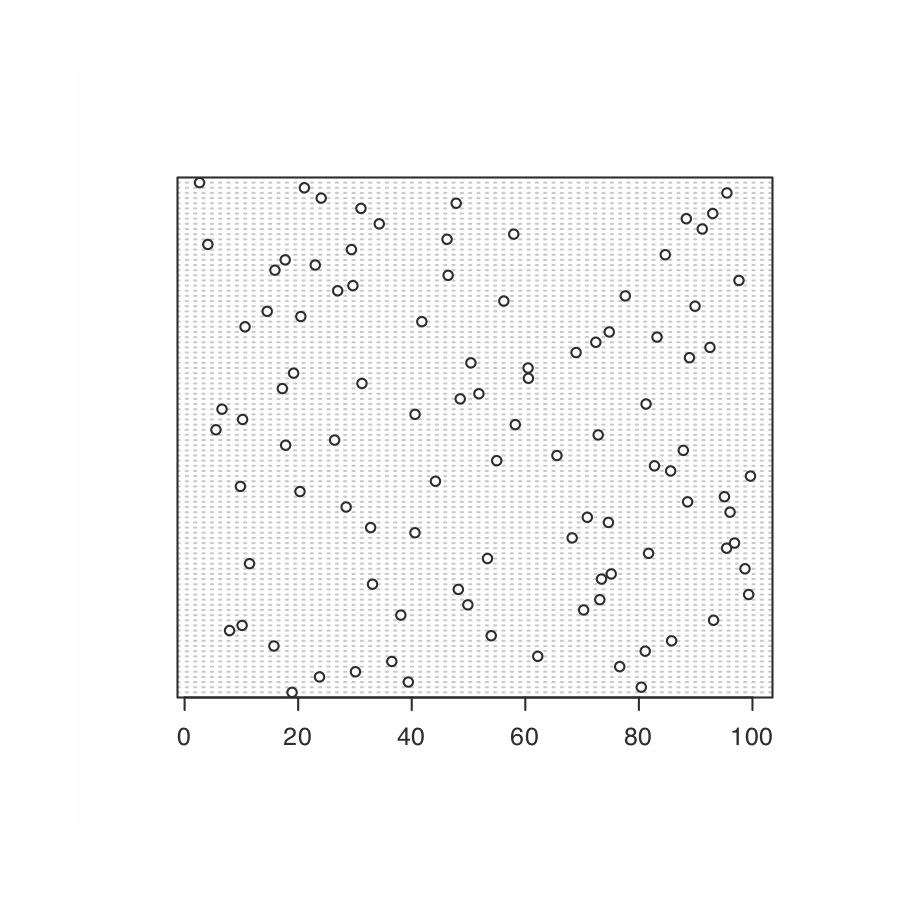
> dotchart (datos)

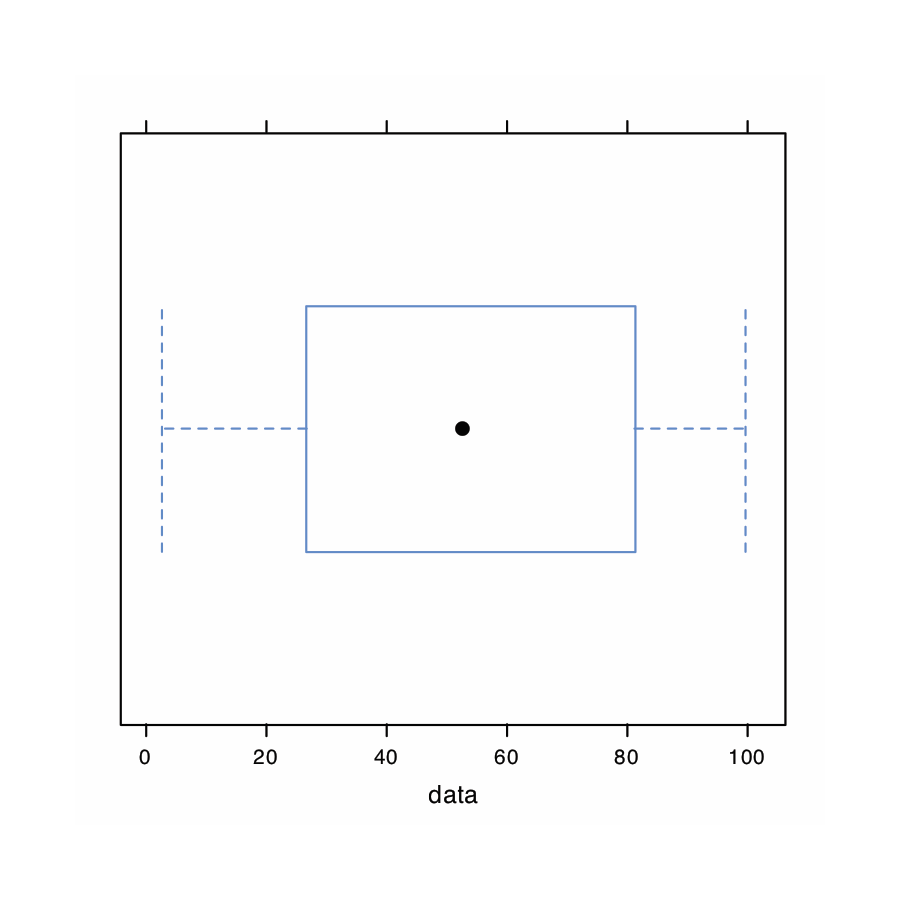
> bwplot (datos)

El histograma (extremo izquierdo) divide los datos en ocho bins, cada uno de los cuales contiene entre 10 y 15 miembros. Como esperamos para una distribución uniforme, el patrón general del histograma sugiere que cada resultado es igualmente probable. Al interpretar la gráfica de densidad del núcleo (segundo desde la izquierda), es importante recordar que trata cada punto de datos como si fuera de una población normalmente distribuida (aunque, en este caso, la población subyacente sea uniforme). Aunque la parcela parece sugerir que hay dos poblaciones normalmente distribuidas, los resultados individuales que se muestran en la parte inferior de la parcela proporcionan evidencia adicional de una distribución uniforme. El gráfico de puntos (segundo desde la derecha) no muestra tendencia a lo largo del eje y, lo que indica que los miembros individuales de esta muestra fueron extraídos al azar de la población. La distribución a lo largo del eje x tampoco muestra ningún patrón, como se esperaba para una distribución uniforme, Finalmente, la gráfica de caja (extrema derecha) no muestra evidencia de valores atípicos.