6.7: Resolviendo problemas de equilibrio

Los diagramas de escalera son una herramienta útil para evaluar la reactividad química y para proporcionar una estimación razonable de la composición de un sistema químico en equilibrio. Si necesitamos una descripción cuantitativa más exacta de la condición de equilibrio, entonces un diagrama de escalera es insuficiente; en cambio, necesitamos encontrar una solución algebraica. En esta sección aprenderemos a configurar y resolver problemas de equilibrio. Comenzaremos con un problema simple y trabajaremos hacia problemas más complejos.

Un simple problema: la solubilidad del Pb (IO ₃) ₂

Si colocamos un compuesto insoluble como Pb (IO ₃) ₂ en agua desionizada, el sólido se disuelve hasta las concentraciones de Pb ^{2 +} y\(\text{IO}_3^-\) satisface el producto de solubilidad para Pb (IO ₃) ₂. En equilibrio la solución se satura con Pb (IO ₃) ₂, lo que significa simplemente que no más sólidos pueden disolverse. ¿Cómo determinamos las concentraciones de equilibrio de Pb ^{2 +} y\(\text{IO}_3^-\), y cuál es la solubilidad molar de Pb (IO ₃) ₂ en esta solución saturada?

Cuando primero agregamos Pb sólido (IO ₃) ₂ al agua, las concentraciones de Pb ^{2 +} y\(\text{IO}_3^-\) son cero y el cociente de reacción, Q _r, es

\[Q_r = \left[\mathrm{Pb}^{2+}\right]\left[\mathrm{IO}_{3}^{-}\right]^{2}=0 \nonumber\]

A medida que el sólido se disuelve, las concentraciones de estos iones aumentan, pero Q _r permanece menor que K _sp. Alcanzamos el equilibrio y “satisfacemos el producto de solubilidad” cuando Q _r = K _sp.

Comenzamos por escribir la reacción de equilibrio y la expresión del producto de solubilidad para Pb (IO ₃) ₂.

\[\mathrm{Pb}\left(\mathrm{IO}_{3}\right)_{2}(s)\rightleftharpoons \mathrm{Pb}^{2+}(a q)+2 \mathrm{IO}_{3}^{-}(a q) \nonumber\]

e \[K_{\mathrm{sp}}=\left[\mathrm{Pb}^{2+}\right]\left[\mathrm{IO}_{3}^{-}\right]^{2}=2.5 \times 10^{-13} \label{6.1}\]

A medida que se disuelve Pb (IO ₃) ₂, se forman dos\(\text{IO}_3^-\) iones por cada ion de Pb ^{2 +}. Si asumimos que el cambio en la concentración molar de Pb ^{2 +} en equilibrio es x, entonces el cambio en la concentración molar de\(\text{IO}_3^-\) es 2 x. La siguiente tabla nos ayuda a realizar un seguimiento de las concentraciones iniciales, el cambio en las centraciones y las concentraciones de equilibrio de Pb2+ y\(\text{IO}_3^-\).

concentraciones	Pb (IO 3) 2 (s)	\(\rightleftharpoons\)	Pb ^2 ^+ (aq)	+	2\(\text{IO}_3^-\) (aq)
inicial	sólido	\ (\ derechaderpoones izquierdos\) ">	0		\ (\ text {IO} _3^-\) (aq) ">0
cambiar	sólido	\ (\ derechaderpoones izquierdos\) ">	+ x		\ (\ text {IO} _3^-\) (aq) ">+ 2 x
equilibrio	sólido	\ (\ derechaderpoones izquierdos\) ">	x		\ (\ text {IO} _3^-\) (aq) ">2 x

Debido a que un sólido, como Pb (IO ₃) ₂, no aparece en la expresión del producto de solubilidad, no es necesario realizar un seguimiento de su concentración. Recuerde, sin embargo, que el valor de K _sp solo se aplica si hay algún Pb sólido (IO ₃) ₂ presente en equilibrio.

Sustituir las concentraciones de equilibrio en la Ecuación\ ref {6.1} y resolver da

\[(x)(2 x)^{2}=4 x^{3}=2.5 \times 10^{-13} \nonumber\]

\[x=3.97 \times 10^{-5} \nonumber\]

Sustituyendo este valor de x de nuevo en las expresiones de concentración de equilibrio por Pb ^{2 +} y\(\text{IO}_3^-\) da sus concentraciones como

\[\left[\mathrm{Pb}^{2+}\right]=x=4.0 \times 10^{-5} \mathrm{M} \text { and }\left[\mathrm{IO}_{3}^{-}\right]=2 x=7.9 \times 10^{-5} \nonumber\]

Debido a que un mol de Pb (IO ₃) ₂ contiene un mol de Pb ^{2 +}, la solubilidad molar de Pb (IO ₃) ₂ es igual a la concentración de Pb ^{2 +}, o\(4.0 \times 10^{-5}\) M.

Podemos expresar la solubilidad de un compuesto de dos maneras: como su solubilidad molar (mol/L) o como su solubilidad en masa (g/L). Asegúrate de expresar tu respuesta con claridad.

Ejercicio 6.7.1

Calcular la solubilidad molar y la solubilidad en masa para Hg ₂ Cl ₂, dada la siguiente reacción de solubilidad y el valor K _sp.

\[\mathrm{Hg}_{2} \mathrm{Cl}_{2}(s)\rightleftharpoons \mathrm{Hg}_{2}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q) \quad K_{\mathrm{sp}}=1.2 \times 10^{-8} \nonumber\]

Responder

Cuando Hg ₂ Cl ₂ se disuelve, se producen dos Cl ^— por cada ion de\(\text{Hg}_2^{2+}\). Si asumimos x es el cambio en la concentración molar de\(\text{Hg}_2^{2+}\), entonces el cambio en la concentración molar de Cl ^— es 2 x. La siguiente tabla nos ayuda a realizar un seguimiento de nuestra solución a este problema.

concentración	Hg 2 Cl 2 (s)	\(\rightleftharpoons\)	\(\text{Hg}_2^{2+}\)(aq)	+	Cl ^— (aq)
inicial	sólido	\ (\ derechaderpoones izquierdos\) ">	\ (\ text {Hg} _2^ {2+}\) (aq) ">0		0
cambiar	sólido	\ (\ derechaderpoones izquierdos\) ">	\ (\ text {Hg} _2^ {2+}\) (aq) ">+ x		+2 x
equilibrio	sólido	\ (\ derechaderpoones izquierdos\) ">	\ (\ text {Hg} _2^ {2+}\) (aq) "> x		2 x

Sustituyendo las concentraciones de equilibrio en la expresión de K _sp por Hg ₂ Cl ₂ da

\[K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(2 \mathrm{x})^{2}=4 x^{3}=1.2 \times 10^{-18} \nonumber\]

\[x=6.69 \times 10^{-7} \nonumber\]

^{Sustituyendo x de nuevo en las expresiones de equilibrio para\(\text{Hg}_2^{2+}\) y Cl, da sus concentraciones como}

\[\left[\mathrm{Hg}_{2}^{2+}\right]=x=6.7 \times 10^{-7} \ \mathrm{M} \quad\left[\mathrm{Cl}^{-}\right]=2 x=1.3 \times 10^{-6} \ \mathrm{M} \nonumber\]

La solubilidad molar es igual a [\(\text{Hg}_2^{2+}\)], o\(6.7 \times 10^{-7}\) mol/L.

Un problema más complejo: el efecto iónico común

El cálculo de la solubilidad de Pb (IO ₃) ₂ en agua desionizada es un problema sencillo porque la disolución del sólido es la única fuente de Pb ^{2 +} y\(\text{IO}_3^-\). Pero ¿y si agregamos Pb (IO ₃) ₂ a una solución de 0.10 M Pb (NO ₃) ₂? Antes de configurar y resolver este problema algebraicamente, piense en la química del sistema y decida si la solubilidad de Pb (IO ₃) ₂ aumentará, disminuirá o seguirá siendo la misma. Empezar un problema pensando en la respuesta probable es un buen hábito para desarrollar. Saber qué respuestas son razonables te ayudará a detectar errores en tus cálculos y te dará más confianza en que tu solución a un problema es correcta. Debido a que la solución ya contiene una fuente de Pb ^{2 +}, podemos usar el principio de Le Chatelier para predecir que la solubilidad de Pb (IO ₃) ₂ es menor que la de nuestro problema anterior.

Comenzamos configurando una tabla que nos ayude a realizar un seguimiento de las concentraciones de Pb ^{2 +} y a\(\text{IO}_3^-\) medida que este sistema se mueve hacia y alcanza el equilibrio.

concentraciones	Pb (IO 3) 2 (s)	\(\rightleftharpoons\)	Pb ^2 ^+ (aq)	+	2\(\text{IO}_3^-\) (aq)
inicial	sólido	\ (\ derechaderpoones izquierdos\) ">	0.10		\ (\ text {IO} _3^-\) (aq) ">0
cambiar	sólido	\ (\ derechaderpoones izquierdos\) ">	+ x		\ (\ text {IO} _3^-\) (aq) ">+ 2 x
equilibrio	sólido	\ (\ derechaderpoones izquierdos\) ">	0.10 + x		\ (\ text {IO} _3^-\) (aq) ">2 x

Sustituyendo las concentraciones de equilibrio en la Ecuación\ ref {6.1}

\[(0.10+x)(2 x)^{2}=2.5 \times 10^{-13} \nonumber\]

y multiplicar los términos en el lado izquierdo de la ecuación nos deja con

\[4 x^{3}+0.40 x^{2}=2.5 \times 10^{-13} \label{6.2}\]

Esta es una ecuación más difícil de resolver que la de la solubilidad de Pb (IO ₃) ₂ en agua desionizada, y su solución no es inmediatamente obvia. Podemos encontrar una solución rigurosa a la Ecuación\ ref {6.2} utilizando paquetes de software computacional y hojas de cálculo, algunas de las cuales se describen en el Capítulo 6.10.

Existen varios enfoques para resolver ecuaciones cúbicas, pero ninguno es computacionalmente fácil usando solo papel y lápiz.

¿Cómo podríamos resolver la Ecuación\ ref {6.2} si no tenemos acceso a una computadora? Un enfoque es utilizar nuestra comprensión de la química para simplificar el problema. Por el principio de Le Chatelier sabemos que una gran concentración inicial de Pb ²⁺ disminuirá significativamente la solubilidad de Pb (IO ₃) ₂. Una suposición razonable es que la concentración inicial de Pb ^{2 +} está muy cerca de su concentración de equilibrio. Si esta suposición es correcta, entonces la siguiente aproximación es razonable

\[\left[\mathrm{Pb}^{2+}\right]=0.10+x \approx 0.10 \nonumber\]

Sustituyendo esta aproximación en la Ecuación\ ref {6.1} y resolviendo por x da

\[(0.10)(2 x)^{2}=0.4 x^{2}=2.5 \times 10^{-13} \nonumber\]

\[x=7.91 \times 10^{-7} \nonumber\]

Antes de aceptar esta respuesta, debemos verificar que nuestra aproximación es razonable. La diferencia entre la concentración real de Pb ^{2 +}, que es 0.10 + x M, y nuestra suposición de que la concentración de Pb ^{2 +} es 0.10 M es\(7.9 \times 10^{-7}\), o\(7.9 \times 10^{-4}\)% de la concentración asumida. Esto es un error despreciable. Si aceptamos el resultado de nuestro cálculo, encontramos que las concentraciones de equilibrio de Pb ^{2 +} y\(\text{IO}_3^-\) son

\[\left[\mathrm{Pb}^{2+}\right]=0.10+x \approx 0.10 \ \mathrm{M} \text { and }\left[\mathrm{IO}_{3}^{-}\right]=2 x=1.6 \times 10^{-6} \ \mathrm{M} \nonumber\]

\[\begin{aligned} \% \text { error } &=\frac{\text { actual }-\text { assumed }}{\text { assumed }} \times 100 \\ &=\frac{(0.10+x)-0.10}{0.10} \times 100 \\ &=\frac{7.91 \times 10^{-7}}{0.10} \times 100 \\ &=7.91 \times 10^{-4} \% \end{aligned} \nonumber\]

La solubilidad molar de Pb (IO ₃) ₂ es igual a la concentración adicional de Pb ^{2 +} en solución, o\(7.9 \times 10^{-4}\) mol/L Como era de esperar, encontramos que Pb (IO ₃) ₂ es menos soluble en presencia de una solución que ya contiene uno de sus iones. Esto se conoce como el efecto de iones comunes.

Como se describe en el siguiente ejemplo, si una aproximación conduce a un error que es inaceptablemente grande, entonces podemos extender el proceso de hacer y evaluar aproximaciones.

Una “regla general” a la hora de hacer una aproximación es que no debe introducir un error superior a ± 5%. Si bien esta no es una elección irrazonable, lo que importa es que el error tenga sentido dentro del contexto del problema que estás resolviendo.

Ejemplo 6.7.1

Calcular la solubilidad de Pb (IO ₃) ₂ en\(1.0 \times 10^{-4}\) M Pb (NO ₃) ₂.

Solución

Si dejamos que x sea igual al cambio en la concentración de Pb ²⁺, entonces las concentraciones de equilibrio de Pb ^{2 +} y\(\text{IO}_3^-\) son

\[\left[\mathrm{P} \mathrm{b}^{2+}\right]=1.0 \times 10^{-4}+ \ x \text { and }\left[\mathrm{IO}_{3}^-\right]=2 x \nonumber\]

Sustituir estas concentraciones en la Ecuación\ ref {6.1} nos deja con

\[\left(1.0 \times 10^{-4}+ \ x\right)(2 x)^{2}=2.5 \times 10^{-13} \nonumber\]

Para resolver esta ecuación para x, hagamos la siguiente suposición

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x \approx 1.0 \times 10^{-4} \ \mathrm{M} \nonumber\]

Resolver para x da su valor como\(2.50 \times 10^{-5}\); sin embargo, cuando sustituimos este valor por x back, encontramos que la concentración calculada de Pb ²⁺ en equilibrio

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x=1.0 \times 10^{-4}+ \ 2.50 \times 10^{-5}=1.25 \times 10^{-4} \ \mathrm{M} \nonumber\]

es 25% mayor que nuestra suposición de\(1.0 \times 10^{-4}\) M. Este error es irrazonablemente grande.

En lugar de gritar de frustración, hagamos una nueva suposición. Nuestra primera suposición, que la concentración de Pb ^{2 +} es\(1.0 \times 10^{-4}\) M, fue demasiado pequeña. La concentración calculada de\(1.25 \times 10^{-4}\) M, por lo tanto, probablemente sea demasiado grande, pero más cercana a la concentración correcta de lo que era nuestra primera suposición. Para nuestra segunda aproximación, supongamos que

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x=1.25 \times 10^{-4} \mathrm{M} \nonumber\]

Sustituyendo en Ecuación\ ref {6.1} y resolviendo por x da su valor como\(2.24 \times 10^{-5}\). La concentración resultante de Pb ^{2 +} es

\[\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ 2.24 \times 10^{-5}=1.22 \times 10^{-4} \ \mathrm{M} \nonumber\]

que difiere de nuestra suposición de\(1.25 \times 10^{-4}\) M en 2.4%. Debido a que la concentración original de Pb ^{2 +} se le da a dos cifras significativas, este es un error más razonable. Nuestra solución final, a dos cifras significativas, es

\[\left[\mathrm{Pb}^{2+}\right]=1.2 \times 10^{-4} \ \mathrm{M} \text { and }\left[\mathrm{IO}_{3}\right]=4.5 \times 10^{-5} \ \mathrm{M} \nonumber\]

y la solubilidad molar de Pb (IO ₃) ₂ es\(2.2 \times 10^{-5}\) mol/L Este enfoque iterativo para resolver los problemas se conoce como el método de aproximaciones sucesivas.

Ejercicio 6.7.2

Calcula la solubilidad molar para Hg ₂ Cl ₂ en NaCl 0.10 M y compara tu respuesta con su solubilidad molar en agua desionizada (ver Ejercicio 6.7.1 ).

Responder

^{Comenzamos por establecer una tabla que nos ayude a realizar un seguimiento de las concentraciones\(\text{Hg}_2^{2+}\) y Cl, a medida que este sistema se mueve hacia y alcanza el equilibrio.}

concentración	Hg 2 Cl 2 (s)	\(\rightleftharpoons\)	\(\text{Hg}_2^{2+}\)(aq)	+	Cl ^— (aq)
inicial	sólido	\ (\ derechaderpoones izquierdos\) ">	\ (\ text {Hg} _2^ {2+}\) (aq) ">0		0.10
cambiar	sólido	\ (\ derechaderpoones izquierdos\) ">	\ (\ text {Hg} _2^ {2+}\) (aq) ">+ x		+2 x
equilibrio	sólido	\ (\ derechaderpoones izquierdos\) ">	\ (\ text {Hg} _2^ {2+}\) (aq) "> x		0.1 + 2 x

Sustituir las concentraciones de equilibrio en la expresión de K _sp por Hg ₂ Cl ₂ nos deja con una ecuación cúbica difícil de resolver.

\[K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(0.10+2 x)^{2}=4 x^{3}+0.40 x^{2}+0.010 x \nonumber\]

Hagamos una suposición para simplificar este problema. Porque esperamos que el valor de x sea pequeño, supongamos que

\[\left[\mathrm{Cl}^{-}\right]=0.10+2 x \approx 0.10 \nonumber\]

Esto simplifica nuestro problema

\[K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(0.10)^{2}=0.010 x=1.2 \times 10^{-18} \nonumber\]

que da el valor de x como\(1.2 \times 10^{-16}\) M. La diferencia entre la concentración real de Cl ^—, que es (0.10 + 2 x) M, y nuestra suposición de que es 0.10 M introduce un error de\(2.4 \times 10^{-13}\)%. Esto es un error despreciable. La solubilidad molar de Hg ₂ Cl ₂ es la misma que la concentración de\(\text{Hg}_2^{2+}\), o\(1.2 \times 10^{-16}\) M. Como era de esperar, la solubilidad molar en NaCl 0.10 M es menor que\(6.7 \times 10^{-7}\) mol/L, que es su solubilidad en agua (ver solución al Ejercicio 6.7.1 ).

Un enfoque sistemático para resolver problemas de equilibrio

Calcular la solubilidad de Pb (IO ₃) ₂ en una solución de Pb (NO ₃) ₂ es más complicado que calcular su solubilidad en agua desionizada. El cálculo, sin embargo, sigue siendo relativamente fácil de organizar y los supuestos simplificadores son bastante obvios. Este problema es razonablemente sencillo porque implica solo una reacción de equilibrio y una constante de equilibrio.

Determinar la composición de equilibrio de un sistema con múltiples reacciones de equilibrio es más complicado. En esta sección se introduce un enfoque sistemático para establecer y resolver problemas de equilibrio. Como se muestra en la Tabla 6.7.1 , este enfoque implica cuatro pasos.

Tabla 6.7.1 . Enfoque sistemático para resolver problemas de equilibrio

Paso 1 Escribir todas las reacciones de equilibrio relevantes y expresiones constantes de equilibrio.

Paso 2 Cuenta las especies únicas que aparecen en las expresiones constantes de equilibrio; estas son tus incógnitas. Tienes suficiente información para resolver el problema si el número de incógnitas es igual al número de expresiones constantes de equilibrio. Si no es así, agregue una ecuación de balance de masa y/o una ecuación de balance de carga. Continuar sumando ecuaciones hasta que el número de ecuaciones sea igual al número de incógnitas.

Paso 3 Combina tus ecuaciones y resuelve por una desconocida. Siempre que sea posible, simplificar el álgebra haciendo suposiciones apropiadas. Si haces una suposición, establece un límite para su error. Esta decisión influye en su evaluación del supuesto.

Paso 4 Revisa tus suposiciones. Si alguna suposición resulta inválida, regrese al paso anterior y continúe resolviendo. El problema está completo cuando tienes una respuesta que no viole ninguno de tus supuestos.

Además de las expresiones constantes de equilibrio, otras dos ecuaciones son importantes para este enfoque sistemático para resolver un problema de equilibrio. La primera de estas ecuaciones es una ecuación de balance de masas, que simplemente es una afirmación de que la materia se conserva durante una reacción química. En una solución de ácido acético, por ejemplo, las concentraciones combinadas del conjugado ácido débil, CH ₃ COOH, y el conjugado base débil, CH ₃ COO ^—, deben ser iguales a la concentración inicial del ácido acético,\(C_{\text{CH}_3\text{COOH}}\).

\[C_{\mathrm{CH}_{\mathrm{3}} \mathrm{COOH}}=\left[\mathrm{CH}_{3} \mathrm{COOH}\right]+\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right] \nonumber\]

Se puede recordar del Capítulo 2 que esta es la diferencia entre una concentración formal y una concentración molar. La variable C representa una concentración formal.

La segunda ecuación es una ecuación de balance de carga, que requiere que la carga positiva total de los cationes sea igual a la carga negativa total de los aniones. Matemáticamente, la ecuación del balance de carga es

\[\sum_{i=1}^{n}\left(z^{+}\right)_{i}\left[{C^{z}}^+\right]_{i} = -\sum_{j=1}^{m}(z^-)_{j}\left[{A^{z}}^-\right]_{j} \nonumber\]

donde [Cz ⁺] _i y [Az ^-] _j son, respectivamente, las concentraciones del ^i-ésimo catión y el j ^ésimo anión, y ( z ⁺) _i y (z ^—) _j son las cargas para el ^i-ésimo catión y el j ^ésimo anión. Cada ion en solución, aunque no aparezca en una reacción de equilibrio, debe aparecer en la ecuación del balance de carga. Por ejemplo, la ecuación del balance de carga para una solución acuosa de Ca (NO ₃) ₂ es

\[2 \times\left[\mathrm{Ca}^{2+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{+}\right]+\left[\mathrm{NO}_{3}^-\right] \nonumber\]

Obsérvese que multiplicamos la concentración de Ca ^{2 +} por dos y que incluimos las concentraciones de H ₃ O ⁺ y OH ^—.

Un saldo de carga es una conservación de una carga. El signo menos frente al término de suma en el lado derecho de la ecuación de saldo de carga asegura que ambas sumas sean positivas. Hay situaciones en las que es imposible escribir una ecuación de saldo de carga porque no tenemos suficiente información sobre la composición de la solución. Por ejemplo, supongamos que fijamos el pH de una solución usando un tampón. Si no se especifica la composición del búfer, entonces no podemos escribir una ecuación de saldo de carga.

Ejemplo 6.7.2

Escribir ecuaciones de balance de masa y una ecuación de balance de carga para una solución 0.10 M de NaHCO ₃.

Solución

Es más fácil hacer un seguimiento de las especies en solución si anotamos las reacciones que definen la composición de la solución. Estas reacciones son la disolución de una sal soluble

\[\mathrm{NaHCO}_{3}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{HCO}_{3}^{-}(a q) \nonumber\]

y las reacciones de disociación ácido-base de\(\text{HCO}_3^-\) y H ₂ O

\[\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CO}_{3}^{2-}(a q) \nonumber\]

\[\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{CO}_{3}(a q) \nonumber\]

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Las ecuaciones de balance de masas son

\[0.10 \mathrm{M}=\left[\mathrm{H}_{2} \mathrm{CO}_{3}\right]+\left[\mathrm{HCO}_{3}^{-}\right]+\left[\mathrm{CO}_{3}^{2-}\right] \nonumber\]

\[0.10 \ \mathrm{M}=\left[\mathrm{Na}^{+}\right] \nonumber\]

y la ecuación del saldo de carga es

\[\left[\mathrm{Na}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{HCO}_{3}^-\right]+2 \times\left[\mathrm{CO}_{3}^{2-}\right] \nonumber\]

Ejercicio 6.7.3

Escriba las ecuaciones apropiadas de balance de masa y balance de carga para una solución que contenga 0.10 M KH ₂ PO ₄ y 0.050 M Na ₂ HPO ₄.

Responder

Para ayudarnos a determinar qué iones están en solución, escribamos toda la reacción necesaria para preparar las soluciones y las reacciones de equilibrio que tienen lugar dentro de estas soluciones. Estas reacciones son la disolución de dos sales solubles

\[\mathrm{KH}_{2} \mathrm{PO}_{4}(s) \longrightarrow \mathrm{K}^{+}(a q)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber\]

\[\mathrm{NaHPO}_{4}(s) \longrightarrow \mathrm{Na}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber\]

y las reacciones de disociación ácido-base para\(\text{H}_2\text{PO}_4^-\),\(\text{HPO}_4^{2-}\). y H ₂ O.

\[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber\]

\[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{3} \mathrm{PO}_{4}(a q) \nonumber\]

\[\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{PO}_{4}^{3-}(a q) \nonumber\]

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Obsérvese que no incluimos la reacción de disociación de bases\(\text{HPO}_4^{2-}\) porque ya contabilizamos su producto\(\text{H}_2\text{PO}_4^-\),, en otra reacción. Las ecuaciones de balance de masas para K ⁺ y Na ⁺ son sencillas

\[\left[\mathrm{K}^{+}\right]=0.10 \ \mathrm{M} \text { and }\left[\mathrm{Na}^{+}\right]=0.10 \ \mathrm{M} \nonumber\]

pero la ecuación del balance de masas para el fosfato requiere un poco más de reflexión. Ambos\(\text{H}_2\text{PO}_4^-\) y\(\text{HPO}_4^{2-}\) producen los mismos iones en solución. Podemos, por lo tanto, imaginar que la solución contiene inicialmente 0.15 M KH ₂ PO ₄, lo que da la siguiente ecuación de balance de masas.

\[\left[\mathrm{H}_{3} \mathrm{PO}_{4}\right]+\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]+\left[\mathrm{HPO}_{4}^{2-}\right]+\left[\mathrm{PO}_{4}^{3-}\right]=0.15 \ \mathrm{M} \nonumber\]

La ecuación del saldo de carga es

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{K}^{+}\right]+\left[\mathrm{Na}^{+}\right] =\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]+2 \times\left[\mathrm{HPO}_{4}^{2-}\right] +3 \times\left[\mathrm{PO}_{4}^{3-}\right]+\left[\mathrm{OH}^{-}\right] \nonumber\]

pH de un ácido débil monoprótico

Para ilustrar el enfoque sistemático para resolver problemas de equilibrio, calculemos el pH de 1.0 M HF. Dos reacciones de equilibrio afectan el pH. La primera, y la más obvia, es la reacción de disociación ácida para HF

\[\mathrm{HF}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{F}^{-}(a q) \nonumber\]

para lo cual la expresión constante de equilibrio es

\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=6.8 \times 10^{-4} \label{6.3}\]

La segunda reacción de equilibrio es la disociación del agua, que es una reacción obvia pero fácilmente descuidada

\[2 \mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.4}\]

Contando incógnitas, encontramos cuatro: [HF], [F ^—], [H ₃ O ⁺], y [OH ^—]. Para resolver este problema necesitamos dos ecuaciones adicionales. Estas ecuaciones son una ecuación de balance de masas sobre el ácido fluorhídrico

\[C_{\mathrm{HF}}=[\mathrm{HF}]+\left[\mathrm{F}^{-}\right]=1.0 \mathrm{M} \label{6.5}\]

y una ecuación de balance de carga

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{F}^{-}\right] \label{6.6}\]

Con cuatro ecuaciones y cuatro incógnitas, estamos listos para resolver el problema. Antes de hacerlo, simplifiquemos el álgebra haciendo dos suposiciones.

Asunción Uno. Debido a que el HF es un ácido débil, sabemos que la solución es ácida. Para una solución ácida es razonable suponer que

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]>>\left[\mathrm{OH}^{-}\right] \nonumber\]

lo que simplifica la ecuación de saldo de carga

\[C_{\mathrm{HF}}=[\mathrm{HF}]=1.0 \ \mathrm{M} \label{6.7}\]

Asunción Dos. Debido a que el HF es un ácido débil, muy poco de él se disocia para formar F ^—. La mayor parte del HF permanece en su forma ácida débil conjugada y es razonable suponer que

\[[\mathrm{HF}]>>\left[\mathrm{F}^{-}\right] \nonumber\]

lo que simplifica la ecuación del balance de masas para

\[C_{\mathrm{HF}}=[\mathrm{HF}]=1.0 \ \mathrm{M} \label{6.8}\]

Para este ejercicio aceptemos una suposición si introduce un error de menos de ± 5%.

Sustituyendo la Ecuación\ ref {6.7} y la Ecuación\ ref {6.8} en la Ecuación\ ref {6.3}, y resolviendo para la concentración de H ₃ O ⁺ nos da

\[\mathrm{K}_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\mathrm{C}_{\mathrm{HF}}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}}{\mathrm{C}_{\mathrm{HF}}}=6.8 \times 10^{-4} \nonumber\]

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a}} C_{\mathrm{HF}}}=\sqrt{\left(6.8 \times 10^{-4}\right)(1.0)}=2.6 \times 10^{-2} \nonumber\]

Antes de aceptar esta respuesta, debemos verificar nuestras suposiciones. La primera suposición es que [OH ^—] es significativamente menor que [H ₃ O ⁺]. Usando la ecuación\ ref {6.4}, encontramos que

\[\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{1.00 \times 10^{-14}}{2.6 \times 10^{-2}}=3.8 \times 10^{-13} \nonumber\]

Claramente esta suposición es aceptable. El segundo supuesto es que [F ^—] es significativamente menor que [HF]. De la Ecuación\ ref {6.7} tenemos

\[\left[\mathrm{F}^{-}\right]=2.6 \times 10^{-2} \ \mathrm{M} \nonumber\]

Debido a que [F ^—] es 2.60% de C _HF, esta suposición también es aceptable. Dado que [H ₃ O ⁺] es\(2.6 \times 10^{-2}\) M, el pH de 1.0 M HF es 1.59.

¿Cómo cambia el cálculo si requerimos que el error introducido en nuestros supuestos sea inferior a ± 1%? En este caso ya no podemos suponer que [HF] >> [F ^—] y no podemos simplificar la ecuación del balance de masas. Resolviendo la ecuación de balance de masa para [HF]

\[[\mathrm{HF}]=C_{\mathrm{HF}}-\left[\mathrm{F}^{-}\right]=C_{\mathrm{HF}}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber\]

y sustituyendo en la K _una expresión junto con la Ecuación\ ref {6.7} da

\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}}{C_{\mathrm{HF}}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

Reorganizar esta ecuación nos deja con una ecuación cuadrática

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}+K_{\mathrm{a}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-K_{\mathrm{a}} C_{\mathrm{HF}}=0 \nonumber\]

que resolvemos usando la fórmula cuadrática

\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber\]

donde a, b y c son los coeficientes en la ecuación cuadrática

\[a x^{2}+b x+c=0 \nonumber\]

Resolver una ecuación cuadrática da dos raíces, solo una de las cuales tiene significación química. Para nuestro problema, las raíces de la ecuación son

\[x=\frac{-6.8 \times 10^{-4} \pm \sqrt{\left(6.8 \times 10^{-4}\right)^{2}-(4)(1)\left(-6.8 \times 10^{-4}\right)}}{(2)(1)} \nonumber\]

\[x=\frac{-6.8 \times 10^{-4} \pm 5.22 \times 10^{-2}}{2} \nonumber\]

\[x=2.57 \times 10^{-2} \text { or }-2.64 \times 10^{-2} \nonumber\]

Solo la raíz positiva es químicamente significativa porque la raíz negativa da una concentración negativa para H ₃ O ⁺. Así, [H ₃ O ⁺] es\(2.57 \times 10^{-2}\) M y el pH es 1.59.

_{Puede extender este enfoque para calcular el pH de una base débil monoprótica reemplazando K a por K b, reemplazando C HF por la concentración de la base débil y resolviendo [OH ^—] en lugar de [H 3 O +} ].

Ejercicio 6.7.4

Calcular el pH de 0.050 M NH ₃. Indique cualquier suposición que haga para resolver el problema, limitando el error para cualquier suposición a ± 5%. El valor de K _b para NH ₃ es\(1.75 \times 10^{-5}\).

Responder

Para determinar el pH de NH ₃ 0.050 M, debemos considerar dos reacciones de equilibrio: la reacción de disociación de bases para NH ₃

\[\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q) \nonumber\]

y la reacción de disociación del agua.

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Estas dos reacciones contienen cuatro especies cuyas concentraciones debemos considerar: NH ₃,\(\text{NH}_4^+\), H ₃ O ⁺, y OH ^—. Necesitamos cuatro ecuaciones para resolver el problema, estas ecuaciones son la ecuación K _b para NH ₃

\[K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=1.75 \times 10^{-5} \nonumber\]

la ecuación de K _w para H ₂ O

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]

una ecuación de balance de masa sobre amoníaco

\[C_{\mathrm{NH}_{3}}=0.050 \ \mathrm{M}=\left[\mathrm{NH}_{3}\right]+\left[\mathrm{NH}_{4}^{+}\right] \nonumber\]

y una ecuación de balance de carga

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber\]

Para resolver este problema, haremos dos suposiciones. Debido a que NH ₃ es una base, nuestra primera suposición es

\[\left[\mathrm{OH}^{-}\right]>>\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber\]

lo que simplifica la ecuación de saldo de carga

\[\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber\]

Debido a que NH ₃ es una base débil, nuestra segunda suposición es

\[\left[\mathrm{NH}_{3}\right]>>\left[\mathrm{NH}_{4}^{+}\right] \nonumber\]

lo que simplifica la ecuación del balance de masas para

\[C_{\mathrm{NH}_{3}}=0.050 \ \mathrm{M}=\left[\mathrm{NH}_{3}\right] \nonumber\]

Sustituir la ecuación de balance de carga simplificada y la ecuación de balance de masa en la ecuación K _b nos deja con

\[K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{OH}^{-}\right]}{C_{\mathrm{NH}_3}}=\frac{\left[\mathrm{OH}^{-}\right]^{2}}{C_{\mathrm{NH_3}}}=1.75 \times 10^{-5} \nonumber\]

\[\left[\mathrm{OH}^{-}\right]=\sqrt{K_{\mathrm{b}} C_{\mathrm{NH_3}}}=\sqrt{\left(1.75 \times 10^{-5}\right)(0.050)}=9.35 \times 10^{-4} \nonumber\]

Antes de aceptar esta respuesta, debemos verificar nuestras dos suposiciones. El primer supuesto es que la concentración de OH ^— es significativamente mayor que la concentración de H ₃ O ⁺. Usando K _w, encontramos que

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{9.35 \times 10^{-4}}=1.07 \times 10^{-11} \nonumber\]

Claramente esta suposición es aceptable. Nuestra segunda suposición es que la concentración de NH ₃ es significativamente mayor que la concentración de\(\text{NH}_4^+\). Usando nuestra ecuación de equilibrio de carga simplificada, encontramos que

\[\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right]=9.35 \times 10^{-4} \nonumber\]

Debido a que la concentración de\(\text{NH}_4^+\) es 1.9% de\(C_{\text{NH}_3}\), nuestro segundo supuesto también es razonable. Dado que [H ₃ O ⁺] es\(1.07 \times 10^{-11}\), el pH es 10.97.

pH de un ácido o base poliprótico

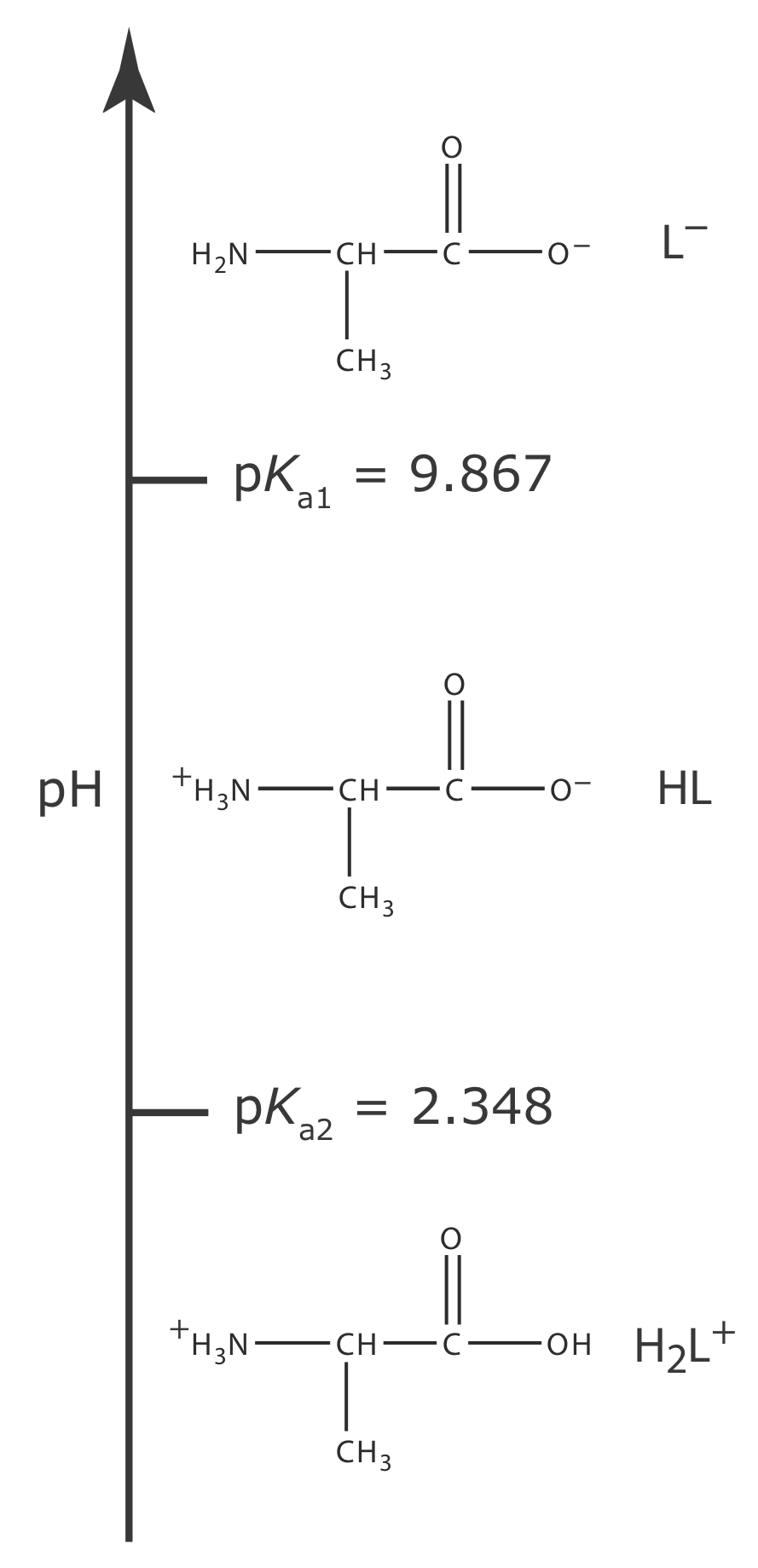
Un problema más desafiante es encontrar el pH de una solución que contenga un ácido débil poliprótico o una de sus especies conjugadas. Como ejemplo, consideremos el aminoácido alanina, cuya estructura se muestra en la Figura 6.7.1 . El diagrama de escalera en la Figura 6.7.2 muestra las tres formas ácido-base de alanina y sus respectivas áreas de predominio. Por simplicidad, identificamos estas especies como H ₂ L ⁺, HL y L ^—.

Figura 6.7.1 . Estructura del aminoácido alanina, que tiene valores de p K a de 2.348 (—COOH) y 9.867 (—NH 2).

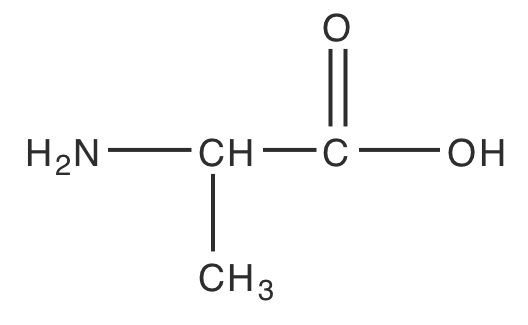
Figura 6.7.2 . Diagrama de escalera para alanina.

pH de Clorhidrato de Alanina 0.10 M (H ₂ L ⁺)

El clorhidrato de alanina es la sal del ácido débil diprótico H ₂ L ⁺ y Cl ^—. Debido a que H ₂ L ⁺ tiene dos reacciones de disociación ácida, una solución sistemática completa a este problema es más complicada que la de un ácido débil monoprótico. El diagrama de escalera en la Figura 6.7.2 nos ayuda a simplificar el problema. Debido a que las áreas de predominio para H ₂ L ⁺ y L ^—están tan separadas, podemos suponer que una solución de H ₂ L ⁺ no contendrá una cantidad significativa de L ^—. Como resultado, podemos tratar H ₂ L ⁺ como si fuera un ácido débil monoprótico. El cálculo del pH del clorhidrato de alanina 0.10 M, que es 1.72, se deja al lector como ejercicio.

pH de 0.10 M Alaninato de Sodio (L ^—)

El ion alaninato es una base débil diprótica. Debido a que L ^— tiene dos reacciones de disociación de bases, una solución sistemática completa a este problema es más complicada que la de una base débil monoprótica. Una vez más, el diagrama de escalera en la Figura 6.7.2 nos ayuda a simplificar el problema. Debido a que las áreas de predominio para H ₂ L ⁺ y L ^—están tan separadas, podemos suponer que una solución de L ^— no contendrá una cantidad significativa de H ₂ L ⁺. Como resultado, podemos tratar a L ^—como si se tratara de una base débil monoprótica. El cálculo del pH de alaninato de sodio 0.10 M, que es 11.42, se deja al lector como ejercicio.

pH de 0.10 M Alanina (HL)

Encontrar el pH de una solución de alanina es más complicado que nuestros dos ejemplos anteriores porque no podemos ignorar la presencia de H ₂ L ⁺ o L ^—. Para calcular el pH de la solución debemos considerar la reacción de disociación ácida de alanina

\[\mathrm{HL}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{L}^{-}(a q) \nonumber\]

y su reacción de disociación de bases

\[\mathrm{HL}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{L}^{+}(a q) \nonumber\]

y, como siempre, también debemos considerar la disociación del agua

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

Esto nos deja con cinco incógnitas— [H ₂ L ⁺], [HL], [L ^—], [H ₃ O ⁺], y [OH ^—] —para lo cual necesitamos cinco ecuaciones. Estas ecuaciones son K _a2 y K _b2 para alanina

\[K_{\mathrm{a} 2}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{L}^{-}\right]}{[\mathrm{HL}]} \nonumber\]

\[K_{\mathrm{b} 2}=\frac{K_{\mathrm{w}}}{K_{\mathrm{a1}}}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]}{[\mathrm{HL}]} \nonumber\]

la ecuación de K _w

\[K_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]

una ecuación de balance de masas para alanina

\[C_{\mathrm{HL}}=\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+[\mathrm{HL}]+[\mathrm{L}^{-}] \nonumber\]

y una ecuación de balance de carga

\[\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{OH}^-]+[\mathrm{L^-}] \nonumber\]

Debido a que el HL es un ácido débil y una base débil, parece razonable suponer que poco de él se disociará y que

\[[\mathrm{HL}]>>\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+[\mathrm{L}^-] \nonumber\]

lo que nos permite simplificar la ecuación del balance de masas para

\[C_{\mathrm{HL}}=[\mathrm{HL}] \nonumber\]

A continuación resolvemos K _b2 para [H ₂ L ⁺]

\[\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]=\frac{K_{\mathrm{w}}[\mathrm{HL}]}{K_{\mathrm{a1}}\left[\mathrm{OH}^{-}\right]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{HL}]}{K_{\mathrm{a1}}}=\frac{C_{\mathrm{HL}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a1}}} \nonumber\]

y resuelve K _a2 para [L ^—]

\[[\mathrm{L^-}]=\frac{K_{a2}[\mathrm{HL}]}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{K_{a2} C_{\mathrm{HL}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

Sustituir estas ecuaciones por [H ₂ L ⁺] y [L ^—], y la ecuación para K _w, en la ecuación de equilibrio de carga nos da

\[\frac{C_{\mathrm{HL}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a1}}}+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}+\frac{K_{a2} C_{\mathrm{HL}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

que simplificamos para

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left(\frac{C_{\mathrm{HL}}}{K_{\mathrm{a1}}}+1\right)=\frac{1}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\left(K_{\mathrm{w}}+K_{a2} C_{\mathrm{HL}}\right) \nonumber\]

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}=\frac{\left(K_{\mathrm{a} 2} C_{\mathrm{HL}}+K_{\mathrm{w}}\right)}{\frac{C_{\mathrm{HL}}}{K_{\mathrm{a1}}}+1}=\frac{K_{\mathrm{a1}}\left(K_{\mathrm{a2}} C_{\mathrm{HL}}+K_{\mathrm{w}}\right)}{C_{\mathrm{HL}}+K_{\mathrm{a1}}} \nonumber\]

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{\frac{\left(K_{\mathrm{a1}} K_{a2} C_{\mathrm{HL}}+K_{\mathrm{a1}} K_{\mathrm{w}}\right)}{C_{\mathrm{HL}}+K_{\mathrm{a1}}}} \nonumber\]

Podemos simplificar aún más esta ecuación si K _a1 K _w << K _a1 K _a2 C _HL, y si K _a1 << C _HL, dejándonos con

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a1}} K_{\mathrm{a} 2}} \nonumber\]

Para una solución de alanina 0.10 M el [H ₃ O ⁺] es

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{\left(4.487 \times 10^{-3}\right)\left(1.358 \times 10^{-10}\right)}=7.806 \times 10^{-7} \ \mathrm{M} \nonumber\]

o un pH de 6.11.

Ejercicio 6.7.5

Verificar que cada suposición en nuestra solución para el pH de alanina 0.10 M sea razonable, utilizando ± 5% como límite para el error aceptable.

Responder

Al resolver para el pH de 0.10 M alanina, hicimos los siguientes tres supuestos: (a) [HL] >> [H ₂ L ⁺] + [L ^—]; (b) K _a1 K _w << K _a1 K _a2 C _HL; y c) K _a1 << C _HL. Los supuestos (b) y (c) son fáciles de verificar. El valor de K _a1 (\(4.487 \times 10^{-3}\)) es 4.5% de C _HL (0.10), y K _a1 K w (\(4.487 \times 10^{-17}\)) es 0.074% de K _a1 K _a2 C _HL (\(6.093 \times 10^{-14}\)). Cada uno de estos supuestos introduce un error de menos de ± 5%.

Para probar la suposición (a) necesitamos calcular las concentraciones de H ₂ L ⁺ y L ^—, lo que logramos usando las ecuaciones para K _a1 y K _a2.

\[\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{HL}]}{K_{\mathrm{a1}}}=\frac{\left(7.807 \times 10^{-7}\right)(0.10)}{4.487 \times 10^{-3}}=1.74 \times 10^{-5} \nonumber\]

\[\left[\mathrm{L}^{-}\right]=\frac{K_{a 2}[\mathrm{HL}]}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{\left(1.358 \times 10^{-10}\right)(0.10)}{7.807 \times 10^{-7}}=1.74 \times 10^{-5} \nonumber\]

Debido a que estas concentraciones son menores a ± 5% de C HL, la primera suposición también es aceptable.

Efecto de la complejación sobre la solubilidad

Un método para aumentar la solubilidad de un precipitado es agregar un ligando que forme complejos solubles con uno de los iones del precipitado. Por ejemplo, la solubilidad de AGi aumenta en presencia de NH ₃ debido a la formación del\(\text{Ag(NH}_3)_2^+\) complejo soluble. Como ilustración final del enfoque sistemático para resolver problemas de equilibrio, calculemos la solubilidad molar de AGi en NH ₃ 0.10 M.

Comenzamos por escribir las reacciones de equilibrio relevantes, que incluyen la solubilidad de AgI, la química ácido-base de NH ₃ y H ₂ O, y la química de complejación metal‐ligando entre Ag ⁺ y NH ₃.

\[\begin{array}{c}{\operatorname{AgI}(s)\rightleftharpoons\operatorname{Ag}^{+}(a q)+\mathrm{I}^{-}(a q)} \\ {\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q)} \\ {2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)} \\ {\mathrm{Ag}^{+}(a q)+2 \mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}(a q)}\end{array} \nonumber\]

Esto nos deja con siete incógnitas— [Ag ⁺], [I ^—], [NH ₃], [\(\text{NH}_4^+\)], [OH ^—], [H ₃ O ⁺], y [\(\text{Ag(NH}_3)_2^+\)] y la necesidad de siete ecuaciones. Cuatro de las ecuaciones que necesitamos para resolver este problema son las expresiones constantes de equilibrio

\[K_{\mathrm{sp}}=\left[\mathrm{Ag}^{+}\right]\left[\mathrm{I}^{-}\right]=8.3 \times 10^{-17} \label{6.9}\]

\[K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=1.75 \times 10^{-5} \label{6.10}\]

\[K_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.11}\]

\[\beta_{2}=\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]}{\left[\mathrm{Ag}^{+}\right]\left[\mathrm{NH}_{3}\right]^{2}}=1.7 \times 10^{7} \label{6.12}\]

Todavía necesitamos tres ecuaciones adicionales. La primera de estas ecuaciones es un balance de masas para NH ₃.

\[C_{\mathrm{NH}_{3}}=\left[\mathrm{NH}_{3}\right]+\left[\mathrm{NH}_{4}^{+}\right]+2 \times\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.13}\]

Al escribir esta ecuación de balance de masas multiplicamos la concentración de\(\text{Ag(NH}_3)_2^+\) por dos ya que hay dos moles de NH ₃ por mol de\(\text{Ag(NH}_3)_2^+\). La segunda ecuación adicional es un balance de masas entre yoduro y plata. Debido a que AgI es la única fuente de I ^— y Ag ⁺, cada yoduro en solución debe tener asociado un ion de plata, que puede ser Ag ⁺ o\(\text{Ag(NH}_3)_2^+\); así

\[\left[\mathrm{I}^{-}\right]=\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.14}\]

Finalmente, incluimos una ecuación de saldo de carga.

\[\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{OH}^-]+[\mathrm{I}^-] \label{6.15}\]

Aunque el problema parece desafiante, tres supuestos simplifican enormemente el álgebra.

Asunción Uno. Debido a que la formación del\(\text{Ag(NH}_3)_2^+\) complejo es tan favorable (\(\beta_2\)es\(1.7 \times 10^7\)), hay muy poco Ag ⁺ libre en solución y es razonable suponer que

\[\left[\mathrm{Ag}^{+}\right]<<\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \nonumber\]

Asunción Dos. Debido a que NH ₃ es una base débil, podemos suponer razonablemente que la mayor parte del amoníaco no complejado permanece como NH ₃; así

\[\left[\mathrm{NH}_{4}^{+}\right]<<\left[\mathrm{NH}_{3}\right] \nonumber\]

Asunción Tres. Debido a que K _sp para AGi es significativamente menor que\(\beta_2\) para\(\text{Ag(NH}_3)_2^+\), la solubilidad de AGi probablemente sea lo suficientemente pequeña como para que se necesite muy poco amoníaco para formar el complejo metal-ligando; así

\[\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]<<\left[\mathrm{NH}_{3}\right] \nonumber\]

A medida que usamos estos supuestos para simplificar el álgebra, fijemos ± 5% como límite de error.

La suposición dos y la suposición tres sugieren que la concentración de NH ₃ es mucho mayor que las concentraciones de cualquiera\(\text{NH}_4^+\) o\(\text{Ag(NH}_3)_2^+\), lo que nos permite simplificar la ecuación de balance de masas para NH ₃ a

\[C_{\mathrm{NH}_{3}}=\left[\mathrm{NH}_{3}\right] \label{6.16}\]

Finalmente, usando el supuesto uno, que sugiere que la concentración de\(\text{Ag(NH}_3)_2^+\) es mucho mayor que la concentración de Ag ⁺, simplificamos la ecuación del balance de masas para I ^— a

\[\left[\mathrm{I}^{-}\right]=\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.17}\]

Ahora estamos listos para combinar ecuaciones y resolver el problema. Comenzamos resolviendo la Ecuación\ ref {6.9} para [Ag ⁺] y la sustituimos por\(\beta_2\) (Ecuación\ ref {6.12}), lo que nos deja con

\[\beta_{2}=\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right][\mathrm{I}^-]}{K_{\mathrm{sp}}\left[\mathrm{NH}_{3}\right]^{2}} \label{6.18}\]

A continuación sustituimos la Ecuación\ ref {6.16} y la Ecuación\ ref {6.17} en la Ecuación\ ref {6.18}, obteniendo

\[\beta_{2}=\frac{\left[\mathrm{I}^{-}\right]^{2}}{K_{\mathrm{sp}}\left(C_{\mathrm{NH}_3}\right)^{2}} \label{6.19}\]

Resolviendo Ecuación\ ref {6.19} para [I ^—] da

\[\left[\mathrm{I}^{-}\right]=C_{\mathrm{NH}_3} \sqrt{\beta_{2} K_{s p}} = \\ (0.10) \sqrt{\left(1.7 \times 10^{7}\right)\left(8.3 \times 10^{-17}\right)}=3.76 \times 10^{-6} \ \mathrm{M} \nonumber\]

Debido a que un mol de AgI produce un mol de I ^—, la solubilidad molar de AGi es la misma que la [I ^—], o\(3.8 \times 10^{-6}\) mol/L.

Antes de aceptar esta respuesta necesitamos verificar nuestras suposiciones. Sustituyendo [I ^—] en la Ecuación\ ref {6.9}, encontramos que la concentración de Ag ⁺ es

\[\left[\mathrm{Ag}^{+}\right]=\frac{K_{\mathrm{p}}}{[\mathrm{I}^-]}=\frac{8.3 \times 10^{-17}}{3.76 \times 10^{-6}}=2.2 \times 10^{-11} \ \mathrm{M} \nonumber\]

Sustituyendo las concentraciones de I ^— y Ag+ en la ecuación del balance de masas por yoduro (Ecuación\ ref {6.14}), da la concentración de\(\text{Ag(NH}_3)_2^+\) as

\[\left[\operatorname{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]=[\mathrm{I}^-]-\left[\mathrm{Ag}^{+}\right]=3.76 \times 10^{-6}-2.2 \times 10^{-11}=3.76 \times 10^{-6} \ \mathrm{M} \nonumber\]

Nuestra primera suposición de que [Ag ⁺] es significativamente menor que la [\(\text{Ag(NH}_3)_2^+\)] es razonable.

Sustituyendo las concentraciones de Ag ⁺ y\(\text{Ag(NH}_3)_2^+\) en la Ecuación\ ref {6.12} y resolviendo [NH ₃], da

\[\left[\mathrm{NH}_{3}\right]=\sqrt{\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]}{\left[\mathrm{Ag}^{+}\right] \beta_{2}}}=\sqrt{\frac{3.76 \times 10^{-6}}{\left(2.2 \times 10^{-11}\right)\left(1.7 \times 10^{7}\right)}}=0.10 \ \mathrm{M} \nonumber\]

De la ecuación de balance de masas para NH3 (Ecuación\ ref {6.12}) vemos que [\(\text{NH}_4^+\)] es insignificante, verificando nuestra segunda suposición que\([\text{NH}_4^+]\) es significativamente menor que [NH ₃]. Nuestra tercera suposición de que [\(\text{Ag(NH}_3)_2^+\)] es significativamente menor que [NH ₃] también es razonable.

¿Se dio cuenta de que nuestra solución a este problema no hizo uso de la Ecuación\ ref {6.15}, la ecuación del saldo de carga? La razón de esto es que no intentamos resolver la concentración de las siete especies. Si necesitamos conocer la composición completa de la mezcla de reacción en equilibrio, entonces tendremos que incorporar la ecuación de equilibrio de carga en nuestra solución.