6.8: Soluciones Buffer
- Page ID
- 75740
Agregar tan poco como 0.1 mL de HCl concentrado a un litro de H 2 O desplaza el pH de 7.0 a 3.0. Agregar la misma cantidad de HCl a un litro de una solución que 0.1 M en ácido acético y 0.1 M en acetato de sodio, sin embargo, da como resultado un cambio insignificante en el pH. ¿Por qué estas dos soluciones responden de manera tan diferente a la adición de HCl?
Una mezcla de ácido acético y acetato de sodio es un ejemplo de un tampón ácido-base. Para entender cómo funciona este tampón para limitar el cambio en el pH, debemos considerar su reacción de disociación ácida
\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]
y su correspondiente constante de disociación ácida
Tomando el log negativo de los términos en la Ecuación\ ref {6.1} y resolviendo para pH nos deja con el resultado que se muestra aquí.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]
Tal vez recuerde que desarrollamos estas mismas ecuaciones en el Capítulo 6.6 cuando introdujimos diagramas de escalera.
El amortiguamiento ocurre debido a la relación logarítmica entre el pH y la relación de concentración de acetato y ácido acético. Aquí hay un ejemplo para ilustrar este punto. Si las concentraciones de ácido acético y acetato son iguales, el pH del tampón es 4.76. Si convertimos 10% del acetato en ácido acético, al agregar un ácido fuerte, la relación [CH 3 COO —]/[CH 3 COOH] cambia de 1.00 a 0.818, y el pH disminuye de 4.76 a 4.67, una disminución de solo 0.09 unidades de pH.
La relación [CH 3 COO —]/[CH 3 COOH] se convierte en 0.9/1.1 = 0.818 y el pH se convierte en
\[\mathrm{pH}=4.76+\log (0.818)=4.67 \nonumber\]
Solución sistemática a problemas de búfer
La ecuación\ ref {6.2} se escribe en términos de las concentraciones de equilibrio de CH 3 COOH y de CH 3 COO —. Una relación más útil relaciona el pH de un tampón con las concentraciones iniciales del ácido débil y la base débil. Podemos derivar una ecuación general de tampón considerando las siguientes reacciones para un ácido débil, HA, y la sal soluble de su base débil conjugada, NaA.
\[\begin{array}{c}{\mathrm{NaA}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{A}^{-}(a q)} \\ {\mathrm{HA}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{A}^{-}(a q)} \\ {2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)}\end{array} \nonumber\]
Debido a que se desconocen las concentraciones de Na +, A —, HA, H 3 O + y OH, necesitamos cinco ecuaciones para definir la composición de la solución. Dos de estas ecuaciones son las expresiones constantes de equilibrio para HA y H 2 O.
\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]
Las tres ecuaciones restantes son ecuaciones de balance de masas para HA y Na +
\[C_{\mathrm{HA}}+C_{\mathrm{NaA}}=[\mathrm{HA}]+\left[\mathrm{A}^{-}\right] \label{6.4}\]
\[C_{\mathrm{NaA}}=\left[\mathrm{Na}^{+}\right] \label{6.5}\]
y una ecuación de balance de carga
Sustituyendo la ecuación\ ref {6.5} en la ecuación\ ref {6.6} y resolviendo [A —] da
A continuación, sustituimos la Ecuación\ ref {6.7} por la Ecuación\ ref {6.4}, que da la concentración de HA como
Finalmente, sustituimos la Ecuación\ ref {6.7} y la Ecuación\ ref {6.8} por la Ecuación\ ref {6.3} y resolvemos que el pH llegue a una ecuación general para el pH de un tampón.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{C_{\mathrm{NaA} }-\left[\mathrm{OH}^{-}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{C_{\mathrm{HA}}+\left[\mathrm{OH}^{-}\right]-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]
Si las concentraciones iniciales del ácido débil, C HA, y la base débil, C NaA. son significativamente mayores que [H 3 O +] y [OH —], entonces podemos simplificar la ecuación general al Henderson— Ecuación de Hasselbalch.
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{C_{\mathrm{NaA}}}{C_{\mathrm{HA}}} \label{6.9}\]
Como se describe a continuación, la ecuación Henderson—Hasselbalch proporciona una manera simple de calcular el pH de un tampón y determinar el cambio en el pH al agregar un ácido fuerte o una base fuerte.
Lawrence Henderson (1878‐1942) desarrolló por primera vez una relación entre [H 3 O +], [HA] y [A —] mientras estudiaba el tamponamiento de la sangre. Kurt Hasselbalch (1874‐1962) modificó la ecuación de Henderson transformándola a la forma logarítmica mostrada en la Ecuación\ ref {6.9}. Los supuestos que conducen a la Ecuación\ ref {6.9} dan como resultado un error mínimo en el pH (<± 5%) para concentraciones mayores de HA y A —, para concentraciones de HA y A — que son similares en magnitud, y para ácidos débiles con valores de p K a más cercanos a 7. Para la mayoría de los problemas de este libro de texto, la Ecuación\ ref {6.9} proporciona resultados aceptables. No obstante, asegúrate de poner a prueba tus suposiciones. Para una discusión de la ecuación Henderson—Hasselbalch, incluyendo el error inherente a la Ecuación\ ref {6.9}, véase Po, H. N.; Senozan, N. M. “La ecuación de Henderson—Hasselbalch: su historia y limitaciones”, J. Chem. Educ. 2001, 78, 1499—1503.
Calcular el pH de un tampón que es 0.020 M en NH 3 y 0.030 M en NH 4 Cl. ¿Cuál es el pH después de agregar 1.0 mL de NaOH 0.10 M a 0.10 L de este tampón?
Solución
La constante de disociación ácida para\(\text{NH}_4^+\) es\(5.70 \times 10^{-10}\), que es una p K a de 9.24. Sustituyendo las concentraciones iniciales de NH 3 y NH 4 Cl en la Ecuación\ ref {6.9} y resolviendo, encontramos que el pH del tampón es
\[\mathrm{pH}=9.24+\log \frac{0.020}{0.030}=9.06 \nonumber\]
Con un pH de 9.06, la concentración de H 3 O + es\(8.71 \times 10^{-10}\) y la concentración de OH — es\(1.15 \times 10^{-5}\). Debido a que ambas concentraciones son mucho menores que cualquiera\(C_{\text{NH}_3}\) o\(C_{\text{NH}_4\text{Cl}}\), las aproximaciones utilizadas para derivar la Ecuación\ ref {6.9} son razonables.
La adición de NaOH convierte una porción del\(\text{NH}_4^+\) NH 3 después de la reacción
\[\mathrm{NH}_{4}^{+}(a q)+\mathrm{OH}^{-}(a q) \rightleftharpoons \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{NH}_{3}(a q) \nonumber\]
Debido a que la constante de equilibrio de esta reacción es tan grande (es igual a (K b) -1 o\(5.7 \times 10^4\)), podemos tratar la reacción como si llegara a completarse. Las nuevas concentraciones de\(\text{NH}_4^+\) y NH 3 son
\[C_{\mathrm{NH}_{4}^{+}}=\frac{\operatorname{mol} \ \mathrm{NH}_{4}^{+}- \ \mathrm{mol} \mathrm{OH}^{-}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{NH}_4^+}=\frac{(0.030 \ \mathrm{M})(0.10 \ \mathrm{L})-(0.10 \ \mathrm{M})\left(1.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+1.0 \times 10^{-3} \ \mathrm{L}}=0.029 \ \mathrm{M} \nonumber\]
\[C_{\mathrm{NH}_{3}}=\frac{\mathrm{mol} \ \mathrm{NH}_{3}+\mathrm{mol} \ \mathrm{OH}^{-}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{NH}_3}=\frac{(0.020 \ \mathrm{M})(0.10 \ \mathrm{L})+(0.10 \ \mathrm{M})\left(1.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+1.0 \times 10^{-3} \ \mathrm{L}}=0.021 \ \mathrm{M} \nonumber\]
Sustituir estas concentraciones en la ecuación 6.60 da un pH de
\[\mathrm{pH}=9.24+\log \frac{0.021}{0.029}=9.10 \nonumber\]
Tenga en cuenta que al agregar NaOH se incrementa el pH de 9.06 a 9.10. Como esperamos, agregar una base hace que el pH sea más básico. Comprobando para ver que el pH cambia en la dirección correcta es una forma de detectar un error de cálculo.
Calcular el pH de un tampón que es 0.10 M en KH 2 PO 4 y 0.050 M en Na 2 HPO 4. Cuál es el pH después agregamos 5.0 mL de HCl 0.20 M a 0.10 L de este tampón. Use el Apéndice 11 para encontrar el valor K a apropiado.
- Contestar
-
La constante de disociación ácida para\(\text{H}_2\text{PO}_4^-\) es\(6.32 \times 10^{-8}\), o una p K a de 7.199. Sustituyendo las concentraciones iniciales de\(\text{H}_2\text{PO}_4^-\) y\(\text{HPO}_4^{2-}\) en la Ecuación\ ref {6.9} y resolviendo da el pH del tampón como
\[\mathrm{pH}=7.199+\log \frac{\left[\mathrm{HPO}_{4}^{2-}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]}=7.199+\log \frac{0.050}{0.10}=6.898 \approx 6.90\nonumber\]
La adición de HCl convierte una porción de\(\text{HPO}_4^{2-}\) a\(\text{H}_2\text{PO}_4^-\) como resultado de la siguiente reacción
\[\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{3} \mathrm{O}^{+}(a q)\rightleftharpoons \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber\]
Debido a que la constante de equilibrio de esta reacción es tan grande (lo es\(1.59 \times 10^7\)), podemos tratar la reacción como si llegara a completarse. Las nuevas concentraciones de\(\text{H}_2\text{PO}_4^-\) y\(\text{HPO}_4^{2-}\) son
\[C_{\mathrm{H}_{2} \mathrm{PO}_{4}^{4-}}=\frac{\mathrm{mol} \ \mathrm{H}_{2} \mathrm{PO}_{4}^{-}+\mathrm{mol} \ \mathrm{HCl}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{H}_{2} \mathrm{PO}_{4}^{4-}}=\frac{(0.10 \ \mathrm{M})(0.10 \ \mathrm{L})+(0.20 \ \mathrm{M})\left(5.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+5.0 \times 10^{-3} \ \mathrm{L}}=0.105 \ \mathrm{M} \nonumber\]
\[C_{\mathrm{HPO}_{4}^{2-}}=\frac{\mathrm{mol} \ \mathrm{HPO}_{4}^{2-}-\mathrm{mol} \ \mathrm{HCl}}{V_{\mathrm{total}}} \nonumber\]
\[C_{\mathrm{HPO}_{4}^{2-}}=\frac{(0.05 \ \mathrm{M})(0.10 \ \mathrm{L})-(0.20 \ \mathrm{M})\left(5.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+5.0 \times 10^{-3} \ \mathrm{L}}=0.0381 \ \mathrm{M} \nonumber\]
Sustituyendo estas concentraciones en la Ecuación\ ref {6.9} da un pH de
\[\mathrm{pH}=7.199+\log \frac{\left[\mathrm{HPO}_{4}^{2-}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]}=7.199+\log \frac{0.0381}{0.105}=6.759 \approx 6.76 \nonumber\]
Como esperamos, la adición de HCl disminuye el pH del tampón en una pequeña cantidad, bajando de 6.90 a 6.76.
Podemos usar un ácido débil multiprótico para preparar tampones a tantos pH diferentes como protones ácidos, aplicándose la ecuación Henderson—Hasselbalch en cada caso. Por ejemplo, para el ácido malónico (p K a1 = 2.85 y p K a2 = 5.70) podemos preparar tampones con valores de pH de
\[\begin{array}{l}{\mathrm{pH}=2.85+\log \frac{C_{\mathrm{HM}^{-}}}{C_{\mathrm{H}_{2} \mathrm{M}}}} \\ {\mathrm{pH}=5.70+\log \frac{C_{\mathrm{M}^{2-}}}{C_{\mathrm{HM}^-}}}\end{array} \nonumber\]
donde H 2 M, HM y M 2 son diferentes formas ácido-base del ácido malónico.
Aunque nuestro tratamiento de tampones se basa en la química ácido-base, podemos extender los tampones a equilibrios que implican complejación o reacciones redox. Por ejemplo, la ecuación de Nernst para una solución que contiene Fe 2 + y Fe 3 + es similar en forma a la ecuación de Henderson‐Hasselbalch.
\[E=E_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}^{\circ}-0.05916 \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]} \nonumber\]
Una solución que contiene concentraciones similares de Fe 2 + y Fe 3 + se tampona a un potencial cercano al potencial de reducción del estado estándar para Fe 3 +. Llamamos a tales soluciones tampones redox. Agregar un agente oxidante fuerte o un agente reductor fuerte a un tampón redox da como resultado un pequeño cambio en el potencial.
Representando soluciones de búfer con diagramas de escalera
Un diagrama de escalera proporciona una manera sencilla de visualizar las especies predominantes de una solución en función de las condiciones de la solución. También proporciona una manera conveniente de mostrar el rango de condiciones de solución sobre las cuales un búfer es efectivo. Por ejemplo, existe un tampón ácido-base cuando las concentraciones del ácido débil y su base débil conjugada son similares. Por conveniencia, supongamos que existe un búfer ácido-base cuando
\[\frac{1}{10} \leq \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \leq \frac{10}{1} \nonumber\]
Sustituir estas proporciones en la ecuación de Henderson—Hasselbalch
\[\begin{aligned} \mathrm{pH} &=\mathrm{p} K_{\mathrm{a}}+\log \frac{1}{10}=\mathrm{p} K_{\mathrm{a}}-1 \\ \mathrm{pH} &=\mathrm{p} K_{\mathrm{a}}+\log \frac{10}{1}=\mathrm{p} K_{\mathrm{a}}+1 \end{aligned} \nonumber\]
muestra que un tampón ácido-base funciona en un rango de pH de p K a ± 1.
Usando el mismo enfoque, es fácil demostrar que existe un tampón de complejación de ligando de metal para ML n cuando
\[\mathrm{pL}=\log K_{n} \pm 1 \text { or } \mathrm{pL}=\log \beta_{n} \pm \frac{1}{n} \nonumber\]
donde K n o\(\beta_n\) es la constante de formación escalonada o global relevante. Para un agente oxidante y su agente reductor conjugado, existe un tampón redox cuando
\[E=E^{\circ} \pm \frac{1}{n} \times \frac{R T}{F}=E^{\circ} \pm \frac{0.05916}{n}\left(\text { at } 25^{\circ} \mathrm{C}\right) \nonumber\]
La figura 6.8.1 muestra diagramas de escalera con regiones de búfer para varios sistemas de equilibrio.
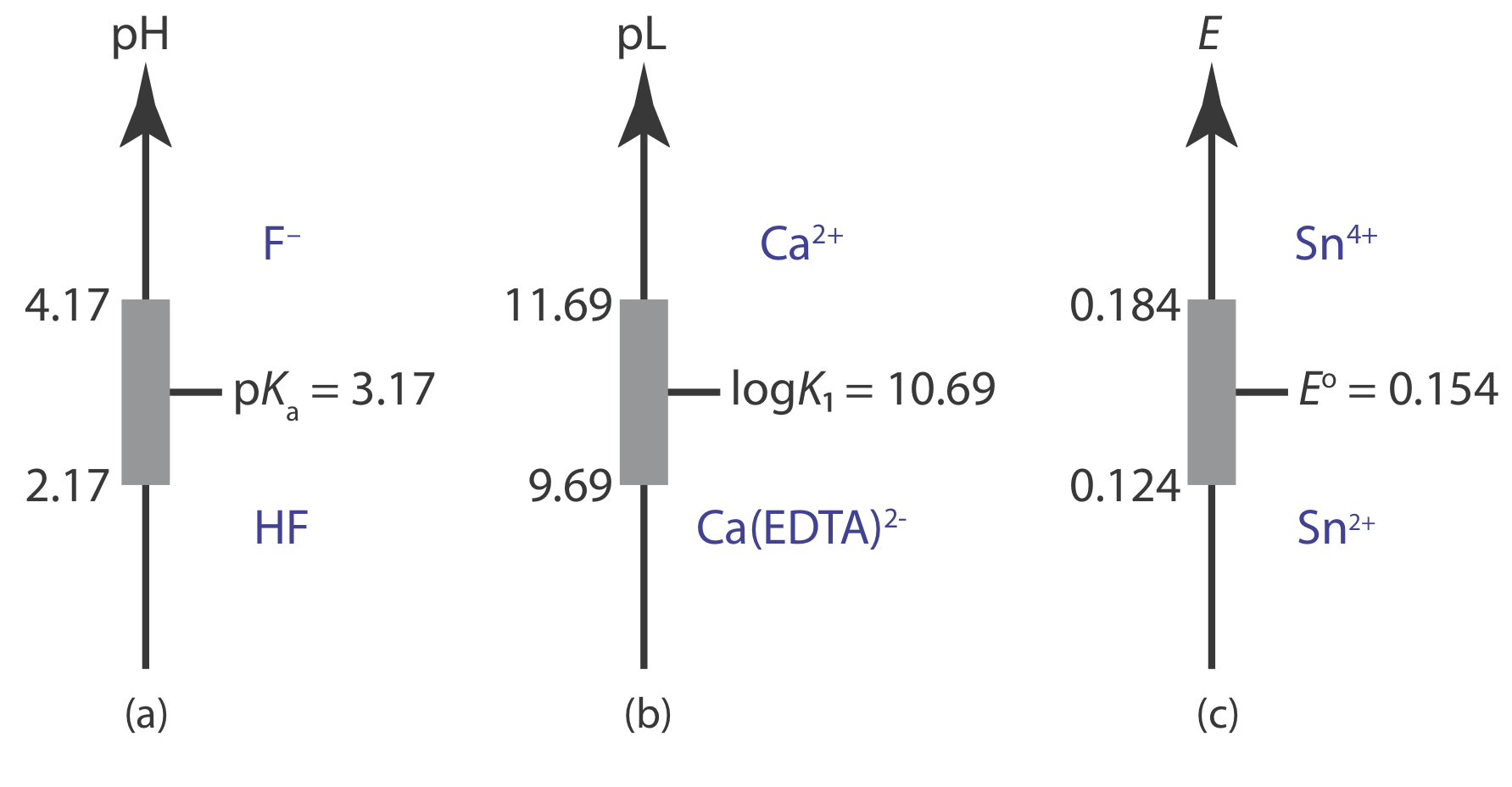
Preparación de un búfer
La capacidad de tampón es la capacidad de un tampón para resistir un cambio en el pH cuando le agregamos un ácido fuerte o una base fuerte. La capacidad de un tampón para resistir un cambio en el pH es función de las concentraciones del ácido débil y la base débil, así como de sus proporciones relativas. La importancia de la concentración del ácido débil y la concentración de la base débil es obvia. Cuantos más moles de ácido débil y base débil tenga un tampón, más base fuerte o ácido fuerte podrá neutralizar sin un cambio significativo en su pH.
Aunque una mayor concentración de agentes tamponantes proporciona mayor capacidad tampón, existen razones para usar concentraciones más pequeñas, incluyendo la formación de precipitados no deseados y la tolerancia de sistemas biológicos a altas concentraciones de sales disueltas.
Las proporciones relativas de un ácido débil y una base débil también afectan cuánto cambia el pH cuando agregamos un ácido fuerte o una base fuerte. Un tampón equimolar en ácido débil y base débil requiere una mayor cantidad de ácido fuerte o base fuerte para provocar un cambio de pH de una unidad. En consecuencia, un tampón es más efectivo contra la adición de ácidos fuertes o bases fuertes cuando su pH está cerca del valor p K a del ácido débil.
Las soluciones tampón a menudo se preparan utilizando “recetas” estándar que se encuentran en la literatura química [ver, por ejemplo, (a) Bower, V. E.; Bates, R. G. J. Res. Natl. Bur. De pie. (U. S.) 1955, 55, 197— 200; b) Bates, R. G. Ann. N. Y. Acad. Sci. 1961, 92, 341—356; c) Bates, R. G. Determinación del pH, 2a ed.; Wiley‐Interscience: Nueva York, 1973]. Además, existen programas de computadora y calculadoras en línea para ayudar en la preparación de búferes [(a) Lambert, W. J. J. Chem. Educ. 1990, 67, 150—153; b) http://www.bioinformatics.org/JaMBW/5/4/index.html.]. Quizás la forma más sencilla de hacer un tampón, sin embargo, es preparar una solución que contenga un conjugado adecuado ácido débil y base débil, medir su pH, y luego ajustar el pH al valor deseado agregando pequeñas porciones de un ácido fuerte o una base fuerte.
Una buena “regla general” a la hora de elegir un tampón es seleccionar uno cuyos reactivos tengan un valor p K a cercano al pH deseado.