7.1: La importancia del muestreo

Cuando un fabricante enumera un producto químico como ACS Reagent Grade, debe demostrar que se ajusta a las especificaciones establecidas por la American Chemical Society (ACS). Por ejemplo, las especificaciones ACS para NaBr comercial requieren que la concentración de hierro sea inferior a 5 ppm. Para verificar que un lote de producción cumple con este estándar, el fabricante recolecta y analiza varias muestras, reportando el resultado promedio en la etiqueta del producto (Figura 7.1.1 ).

Figura 7.1.1 . Certificado de análisis para un lote de producción de NaBR. El resultado para el hierro cumple con las especificaciones del ACS, pero el resultado para el potasio no.

Si las muestras individuales no representan con precisión la población de la que se extraen —población que llamamos población objetivo — entonces incluso un análisis cuidadoso producirá un resultado inexacto. Extrapolar un resultado de una muestra a su población objetivo siempre introduce un determinado error de muestreo. Para minimizar este error de muestreo determinado, debemos recolectar la muestra correcta.

Incluso si recolectamos la muestra correcta, los errores de muestreo indeterminados pueden limitar la utilidad de nuestro análisis. La ecuación\ ref {7.1} muestra que un intervalo de confianza sobre la media\(\overline{X}\),, es proporcional a la desviación estándar, s, del análisis

\[\mu=\overline{X} \pm \frac{t s}{\sqrt{n}} \label{7.1}\]

donde n es el número de muestras y t es un factor estadístico que da cuenta de la probabilidad de que el intervalo de confianza contenga el valor verdadero,\(\mu\).

La ecuación\ ref {7.1} debería ser familiar para usted. Consulte el Capítulo 4 para revisar los intervalos de confianza y ver Apéndice 4 para los valores de t.

Cada paso de un análisis aporta un error aleatorio que afecta la desviación estándar general. Para mayor comodidad, dividamos un análisis en dos pasos, recolectando las muestras y analizando las muestras, cada uno de los cuales se caracteriza por una varianza. Utilizando una propagación de la incertidumbre, la relación entre la varianza general, s ², y las varianzas debidas al muestreo\(s_{samp}^2\),, y la varianza debida al método analítico,\(s_{meth}^2\), es

\[s^{2}=s_{samp}^{2}+s_{meth}^{2} \label{7.2}\]

Aunque la Ecuación\ ref {7.1} se escribe en términos de una desviación estándar, s, una propagación de la incertidumbre se escribe en términos de varianzas, s ². En esta sección, y las que siguen, utilizaremos tanto las desviaciones estándar como las varianzas para discutir la incertidumbre del muestreo. Para una revisión de la propagación de la incertidumbre, véanse el Capítulo 4.3 y el Apéndice 2.

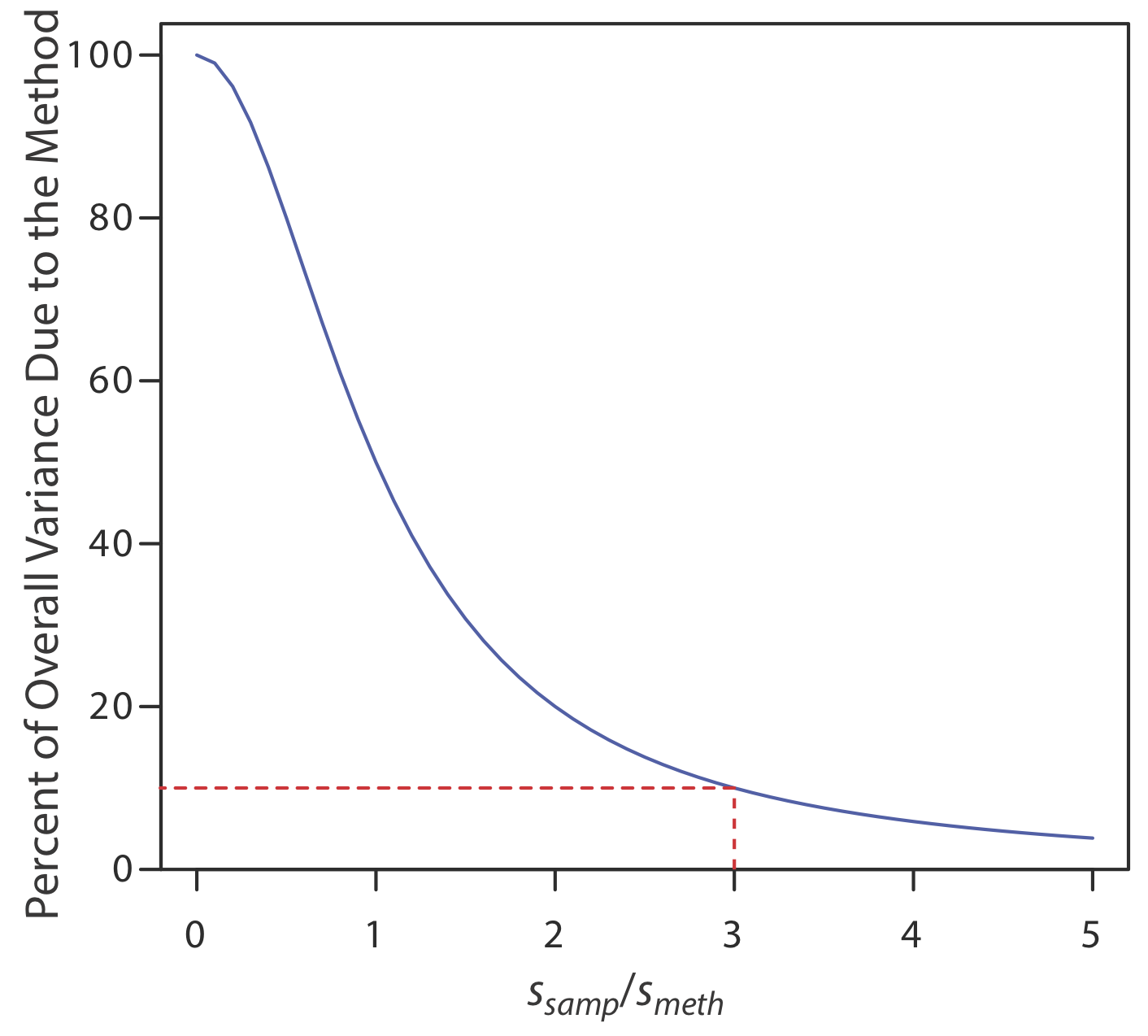
La ecuación\ ref {7.2} muestra que la varianza general para un análisis está limitada por el método analítico o muestreo, o por ambos. Desafortunadamente, los analistas a menudo intentan minimizar la varianza general mejorando solo la precisión del método. Esto es un esfuerzo inútil, sin embargo, si la desviación estándar para el muestreo es más de tres veces mayor que la del método [Youden, Y. J. J. Assoc. Apagado. Anal. Chem. 1981, 50, 1007—1013]. La figura 7.1.2 muestra cómo la relación s _samp/ s _meth afecta la contribución del método a la varianza general. Como lo muestra la línea discontinua, si la desviación estándar de la muestra es\(3 \times\) la desviación estándar del método, entonces los errores indeterminados del método explican solo el 10% de la varianza general. Si los errores de muestreo indeterminados son significativos, la disminución de la _{metanfetamina} solo proporciona una mejora limitada en la precisión general.

Figura 7.1.2 . La curva azul muestra la contribución del método a la varianza general, s ², en función de la magnitud relativa de la desviación estándar en el muestreo, s _samp, y la desviación estándar del método, s _{metanfetamina}. La línea roja discontinua muestra que el método representa sólo el 10% de la varianza general cuando\(s_{samp}/s_{meth} = 3 \times s_{meth}\). Comprender la importancia relativa de las fuentes potenciales de error indeterminado es importante cuando consideramos cómo mejorar la precisión general del análisis.

Ejemplo 7.1.1

Un análisis cuantitativo da una concentración media de 12.6 ppm para un analito. La desviación estándar del método es de 1.1 ppm y la desviación estándar para el muestreo es de 2.1 ppm. a) ¿Cuál es la varianza general para el análisis? (b) ¿En cuánto cambia la varianza general si mejoramos la _{metanfetamina} en 10% a 0.99 ppm? (c) ¿En cuánto cambia la varianza general si mejoramos s _samp en 10% a 1.9 ppm?

Solución

a) La varianza general es

\[s^{2}=s_{samp}^{2}+s_{meth}^{2}=(2.1 \ \mathrm{ppm})^{2}+(1.1 \ \mathrm{ppm})^{2}=5.6 \ \mathrm{ppm}^{2} \nonumber\]

b) La mejora de la desviación estándar del método cambia la varianza general a

\[s^{2}=(2.1 \ \mathrm{ppm})^{2}+(0.99 \ \mathrm{ppm})^{2}=5.4 \ \mathrm{ppm}^{2} \nonumber\]

La mejora de la desviación estándar del método en un 10% mejora la varianza general en aproximadamente 4%.

c) Cambio de la desviación estándar para el muestreo

\[s^{2}=(1.9 \ \mathrm{ppm})^{2}+(1.1 \ \mathrm{ppm})^{2}=4.8 \ \mathrm{ppm}^{2} \nonumber\]

mejora la varianza general en casi un 15%. Como era de esperar, debido a que s _samp es mayor que s _{metanfetamina}, logramos una mayor mejora en la varianza general cuando enfocamos nuestra atención en los problemas de muestreo.

Ejercicio 7.1.1

Supongamos que desea reducir la varianza general en el Ejemplo 7.1.1 a 5.0 ppm ². Si te enfocas en el método, ¿en qué porcentaje necesitas reducir la _{metanfetamina}? Si te enfocas en el muestreo, ¿en qué porcentaje necesitas reducir s _samp?

Contestar

Para reducir la varianza general mejorando la desviación estándar del método se requiere que

\[s^{2}=5.00 \ \mathrm{ppm}^{2} = s_{samp}^{2}+s_{m e t h}^{2} = (2.1 \mathrm{ppm})^{2}+s_{m e t h}^{2} \nonumber\]

Resolver para s _meth da su valor como 0.768 ppm. En relación con su valor original de 1.1 ppm, esto es una reducción de\(3.0 \times 10^1\)%. Para reducir la varianza general mejorando la desviación estándar para el muestreo se requiere que

\[s^{2}=5.00 \ \mathrm{ppm}^{2} = s_{samp}^{2}+s_{meth}^{2} = s_{samp}^{2}+(1.1 \ \mathrm{ppm})^{2} \nonumber\]

Resolviendo para s _samp da su valor como 1.95 ppm. En relación con su valor original de 2.1 ppm, esto es una reducción de 7.1%.

Para determinar qué paso tiene el mayor efecto en la varianza general, necesitamos medir tanto s _samp como s _meth. El análisis de muestras replicadas proporciona una estimación de la varianza global. Para determinar la varianza del método debemos analizar las muestras bajo condiciones en las que podemos suponer que la varianza del muestreo es insignificante; la varianza del muestreo se determina entonces por la diferencia.

Existen varias formas de minimizar la desviación estándar para el muestreo. Aquí hay dos ejemplos. Un enfoque es utilizar un material de referencia estándar (SRM) que ha sido cuidadosamente preparado para minimizar los errores de muestreo indeterminados. Cuando la muestra es homogénea, como es el caso, por ejemplo, con una muestra acuosa, entonces otro enfoque útil es realizar análisis replicados en una sola muestra.

Ejemplo 7.1.2

Los siguientes datos se recolectaron como parte de un estudio para determinar el efecto de la varianza de muestreo en el análisis de formulaciones de fármaco-alimento animal [Fricke, G. H.; Mischler, P. G.; Staffieri, F. P.; Houmyer, C. L. Anal. Chem. 1987, 59, 1213— 1217].

% de fármaco (w/w)			% de fármaco (w/w)
0.0114	0.0099	0.0105	0.0105	0.0109	0.0107
0.0102	0.0106	0.0087	0.0103	0.0103	0.0104
0.0100	0.0095	0.0098	0.0101	0.0101	0.013
0.0105	0.0095	0.0097

Los datos de la izquierda se obtuvieron bajo condiciones en las que tanto s _samp como s _met contribuyen a la varianza general. Los datos de la derecha se obtuvieron bajo condiciones donde s _samp es insignificante. Determinar la varianza general, y las desviaciones estándar debidas al muestreo y al método analítico. ¿A qué fuente de error indeterminado —el muestreo o el método— debemos dirigir nuestra atención si queremos mejorar la precisión del análisis?

Solución

Usando los datos de la izquierda, la varianza general, s ², es\(4.71 \times 10^{-7}\). Para encontrar la contribución del método a la varianza general\(s_{meth}^2\),, utilizamos los datos de la derecha, obteniendo un valor de\(7.00 \times 10^{-8}\). La varianza por muestreo,\(s_{samp}^2\), es

\[s_{samp}^{2}=s^{2}-s_{meth}^{2} = 4.71 \times 10^{-7}-7.00 \times 10^{-8}=4.01 \times 10^{-7} \nonumber\]

La conversión de varianzas a desviaciones estándar da s _samp as\(6.33 \times 10^{-4}\) y s _meth as\(2.65 \times 10^{-4}\). Debido a que s _samp es más del doble de grande que s _meth, mejorar la precisión del proceso de muestreo tendrá el mayor impacto en la precisión general.

Ejercicio 7.1.2

La densidad de un polímero proporciona una medida de su cristalinidad. La desviación estándar para la determinación de densidad usando una sola muestra de un polímero es\(1.96 \times 10^{-3}\) g/cm ³. La desviación estándar al usar diferentes muestras del polímero es\(3.65 \times 10^{-2}\) g/cm ³. Determinar las desviaciones estándar debidas al muestreo y al método analítico.

Contestar

La desviación estándar del método analítico es\(1.96 \times 10^{-3}\) g/cm ³ ya que esta es la desviación estándar para el análisis de una sola muestra del polímero. La varianza de muestreo es

\[s_{sa m p}^{2}=s^{2}-s_{meth}^{2}= \left(3.65 \times 10^{-2}\right)^{2}-\left(1.96 \times 10^{-3}\right)^{2}=1.33 \times 10^{-3} \nonumber\]

La conversión de la varianza a una desviación estándar da s _meth como\(3.64 \times 10^{-2}\) g/cm ³.