7.2: Diseño de un Plan de Muestreo

Un plan de muestreo debe apoyar los objetivos de un análisis. Por ejemplo, un científico de materiales interesado en caracterizar la química de la superficie de un metal es más probable que elija una superficie recién expuesta, creada escindiendo la muestra al vacío, que una superficie previamente expuesta a la atmósfera. En un análisis cualitativo, una muestra no necesita ser idéntica a la sustancia original siempre que haya suficiente analito presente para asegurar su detección. De hecho, si el objetivo de un análisis es identificar un componente a nivel de traza, puede ser deseable discriminar a los componentes principales al recolectar muestras.

Para una interesante discusión sobre la importancia de un plan de muestreo, ver Buger, J. et al. “¿Los científicos y los pescadores recolectan peces del mismo tamaño? Posibles implicaciones para la evaluación de la exposición”, Environ. Res. 2006, 101, 34—41.

Para un análisis cuantitativo, la composición de la muestra debe representar con precisión la población objetivo, requisito que requiere un plan de muestreo cuidadoso. Entre los temas que debemos considerar están estas cinco preguntas.

1. ¿De dónde dentro de la población objetivo debemos recolectar muestras?
2. ¿Qué tipo de muestras debemos recolectar?
3. ¿Cuál es la cantidad mínima de muestra necesaria para cada análisis?
4. ¿Cuántas muestras debemos analizar?
5. ¿Cómo podemos minimizar la varianza general para el análisis?

Dónde muestrear la población objetivo

Un error de muestreo ocurre cuando la composición de una muestra no es idéntica a su población objetivo. Si la población objetivo es homogénea, entonces podemos recolectar muestras individuales sin considerar dónde recolectamos la muestra. Desafortunadamente, en la mayoría de las situaciones la población objetivo es heterogénea y la atención al lugar donde recolectamos las muestras es importante. Por ejemplo, debido a la sedimentación un medicamento disponible como suspensión oral puede tener una mayor concentración de sus ingredientes activos en el fondo del recipiente. La composición de una muestra clínica, como sangre u orina, puede depender de cuándo se recolecta. El nivel de glucosa en sangre de un paciente, por ejemplo, cambiará en respuesta a comer y hacer ejercicio. Otras poblaciones objetivo muestran una heterogeneidad espacial y temporal. La concentración de O ₂ disuelto en un lago es heterogénea debido tanto a un cambio de estaciones como a fuentes puntuales de contaminación.

La composición de una población objetivo homogénea es la misma independientemente de dónde muestremos, cuándo muestremos, o el tamaño de nuestra muestra. Para una población objetivo heterogénea, la composición no es la misma en diferentes ubicaciones, en diferentes momentos o para diferentes tamaños de muestra.

Si la distribución del analito dentro de la población objetivo es una preocupación, entonces nuestro plan de muestreo debe tener esto en cuenta. Cuando es factible, homogeneizar la población objetivo es una solución sencilla, aunque a menudo esto es impracticable. Además, la homogeneización de una muestra destruye información sobre la distribución espacial o temporal del analito dentro de la población objetivo, información que puede ser de importancia.

Muestreo Aleatorio

El plan de muestreo ideal proporciona una estimación imparcial de las propiedades de la población objetivo. Un muestreo aleatorio es la forma más fácil de satisfacer este requisito [Cohen, R. D. J. Chem. Educ. 1991, 68, 902—903]. A pesar de su aparente simplicidad, una muestra verdaderamente aleatoria es difícil de recolectar. El muestreo fortuito, en el que se recolectan muestras sin un plan de muestreo, no es aleatorio y puede reflejar sesgos involuntarios de un analista.

Aquí hay un método simple para asegurar que recolectamos muestras aleatorias. Primero, dividimos la población objetivo en unidades iguales y asignamos a cada unidad un número único. Luego, usamos una tabla de números aleatorios para seleccionar las unidades a muestrear. El ejemplo 7.2.1 proporciona un ejemplo ilustrativo. El Apéndice 14 proporciona una tabla de números aleatorios que puede usar para diseñar un plan de muestreo.

Ejemplo 7.2.1

Para analizar la resistencia a la tracción de un polímero, se mantienen muestras individuales del polímero entre dos abrazaderas y se estiran. Para evaluar un lote de producción, el plan de muestreo del fabricante requiere recolectar diez muestras de 1 cm de\(\times\) 1 cm de una lámina de polímero de\(\times\) 100 cm y 100 cm. Explicar cómo podemos usar una tabla de números aleatorios para asegurarnos de que recolectamos estas muestras al azar.

Solución

Como muestra la cuadrícula de abajo, dividimos la lámina de polímero en 10 000 cuadrados de 1 cm de\(\times\) 1 cm, cada uno identificado por su número de fila y su número de columna, con números que van del 0 al 99.

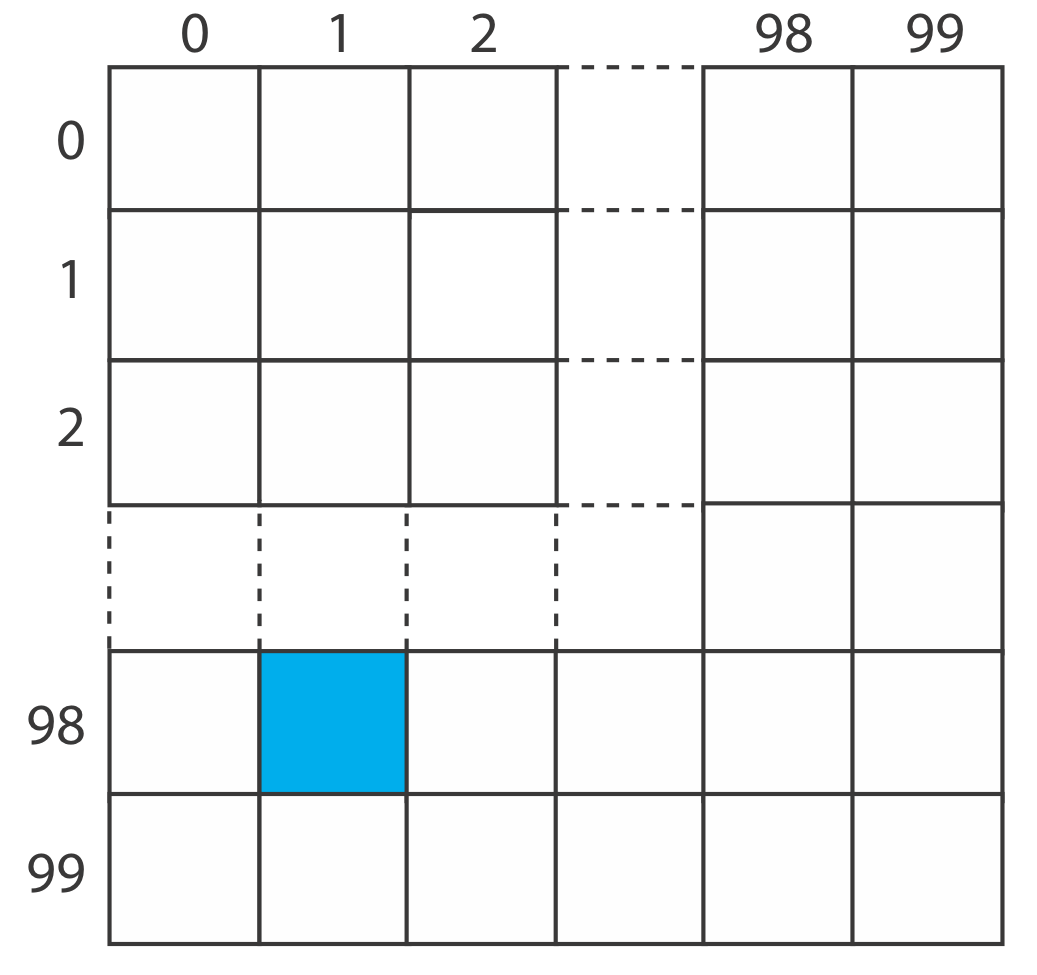
Por ejemplo, el cuadrado azul está en la fila 98 y en la columna 1. Para seleccionar diez cuadrados al azar, ingresamos la tabla de números aleatorios en el Apéndice 14 en un punto arbitrario y dejamos que los últimos cuatro dígitos de la entrada representen el número de fila y el número de columna para la primera muestra. Luego nos movemos por la tabla de una manera predeterminada, seleccionando números aleatorios hasta tener 10 muestras. Para nuestra primera muestra, usemos la segunda entrada en la tercera columna del Apéndice 14, que es 76831. La primera muestra, por lo tanto, es la fila 68 y la columna 31. Si procedemos bajando la tercera columna, entonces las 10 muestras son las siguientes:

muestra	número	fila	columna	muestra	número	roq	columna
1	76831	68	31	6	41701	17	01
2	66558	65	58	7	38605	86	05
3	33266	32	66	8	64516	45	16
4	12032	20	32	9	13015	30	15
5	14063	40	63	10	12138	21	38

Cuando recolectamos una muestra aleatoria no hacemos suposiciones sobre la población objetivo, lo que hace que esta sea el enfoque menos sesgado para el muestreo. Por otro lado, una muestra aleatoria a menudo requiere más tiempo y gasto que otras estrategias de muestreo porque necesitamos recolectar un mayor número de muestras para asegurar que se muestrea adecuadamente la población objetivo, particularmente cuando esa población es heterogénea [Borgman, L. E.; Quimby, W. F. en Keith, L. H., ed. Principles of Environmental Sampling, American Chemical Society: Washington, D. C., 1988, 25—43].

Muestreo de juicio

Lo opuesto al muestreo aleatorio es el muestreo selectivo o de juicio en el que utilizamos información previa sobre la población objetivo para ayudar a guiar nuestra selección de muestras. El muestreo de juicio es más sesgado que el muestreo aleatorio, pero requiere menos muestras. El muestreo crítico es útil si queremos limitar el número de variables independientes que puedan afectar nuestros resultados. Por ejemplo, si estamos estudiando la bioacumulación de PCB en peces, podemos optar por excluir a los peces que son demasiado pequeños, demasiado jóvenes o que parecen enfermos.

Muestreo sistemático

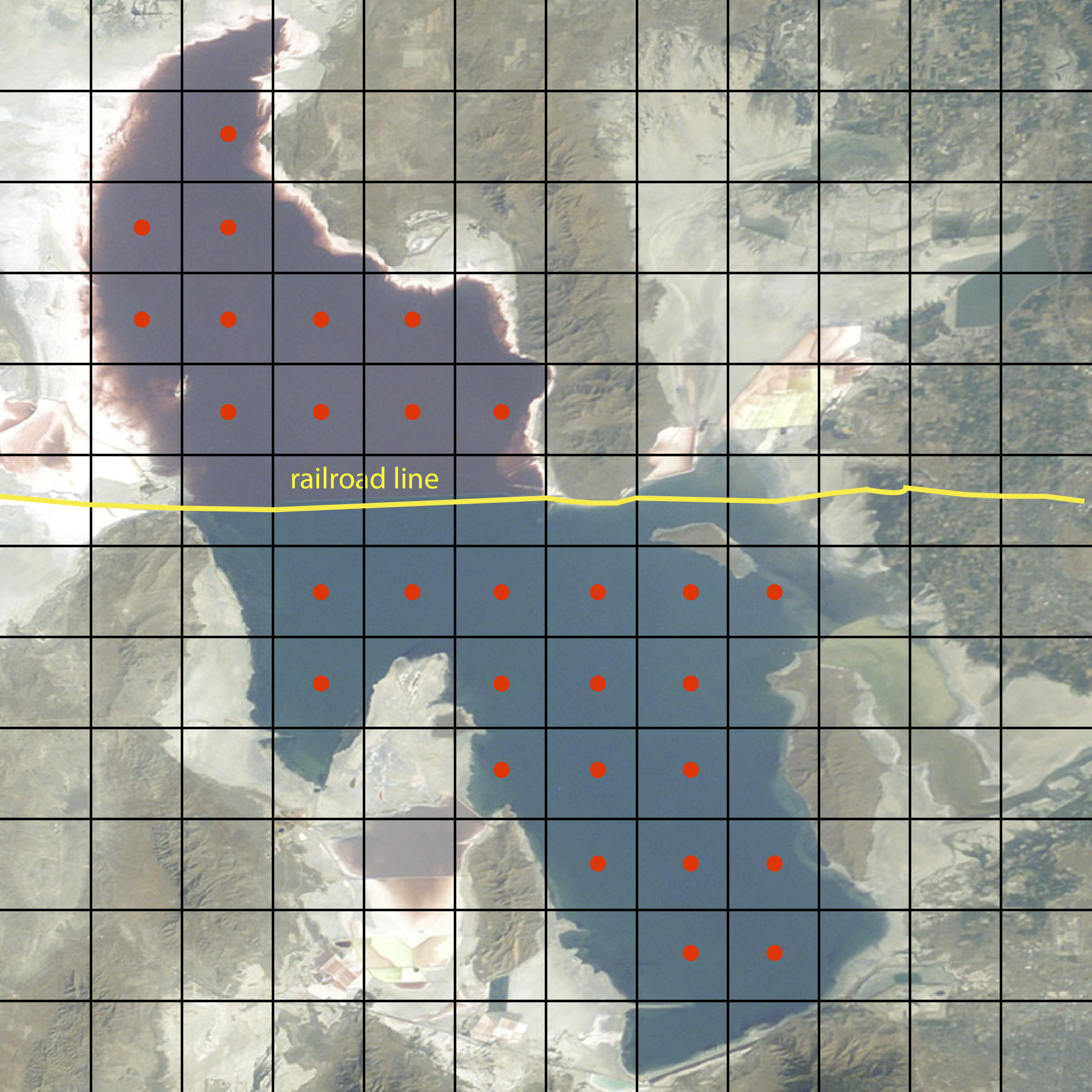
El muestreo aleatorio y el muestreo de juicio representan extremos en el sesgo y en el número de muestras necesarias para caracterizar a la población objetivo. El muestreo sistemático se encuentra entre estos extremos. En el muestreo sistemático se muestrea la población objetivo a intervalos regulares en el espacio o el tiempo. La figura 7.2.1 muestra una foto aérea del Gran Lago Salado en Utah. Una línea de ferrocarril divide el lago en dos secciones que tienen diferentes composiciones químicas. Para comparar las dos secciones del lago y evaluar las variaciones espaciales dentro de cada sección, utilizamos una cuadrícula bidimensional para definir ubicaciones de muestreo, recolectando muestras en el centro de cada ubicación. Cuando una población es heterogénea en el tiempo, como es común en estudios clínicos y ambientales, entonces podríamos elegir recolectar muestras a intervalos regulares en el tiempo.

Figura 7.2.1 . Foto aérea del Gran Lago Salado en Utah, tomada desde la Estación Espacial Internacional a una distancia aproximada de 380 km. La línea del ferrocarril divide el lago en dos tramos que difieren en composición química. La superposición de una rejilla bidimensional divide cada sección del lago en unidades de muestreo. Los puntos rojos en el centro de cada unidad representan sitios de muestreo. Foto cortesía del Laboratorio de Ciencia y Análisis de la Imagen, Centro Espacial Johnson de la NASA, Número de foto ISS007-E-13002 (eol.jsc.nasa.gov).

Si las propiedades de una población objetivo tienen una tendencia periódica, un muestreo sistemático conducirá a un sesgo significativo si nuestra frecuencia de muestreo es demasiado pequeña. Este es un problema común al muestrear señales electrónicas donde el problema se conoce como aliasing. Consideremos, por ejemplo, una señal que sea una simple onda de signo. La figura 7.2.2 a muestra cómo una frecuencia de muestreo insuficiente subestima la frecuencia verdadera de la señal. La señal aparente, mostrada por la línea roja discontinua que pasa por los cinco puntos de datos, es significativamente diferente de la señal verdadera mostrada por la línea azul continua.

Figura 7.2.2 . Efecto de la frecuencia de muestreo al monitorear una señal periódica. Las muestras individuales se muestran por los puntos rojos (•). En (a) la frecuencia de muestreo es de aproximadamente 1.5 muestras por periodo. La línea roja discontinua muestra la señal aparente basada en cinco muestras y la línea azul continua muestra la señal verdadera. En (b) una frecuencia de muestreo de aproximadamente 5 muestras por periodo reproduce con precisión la señal verdadera.

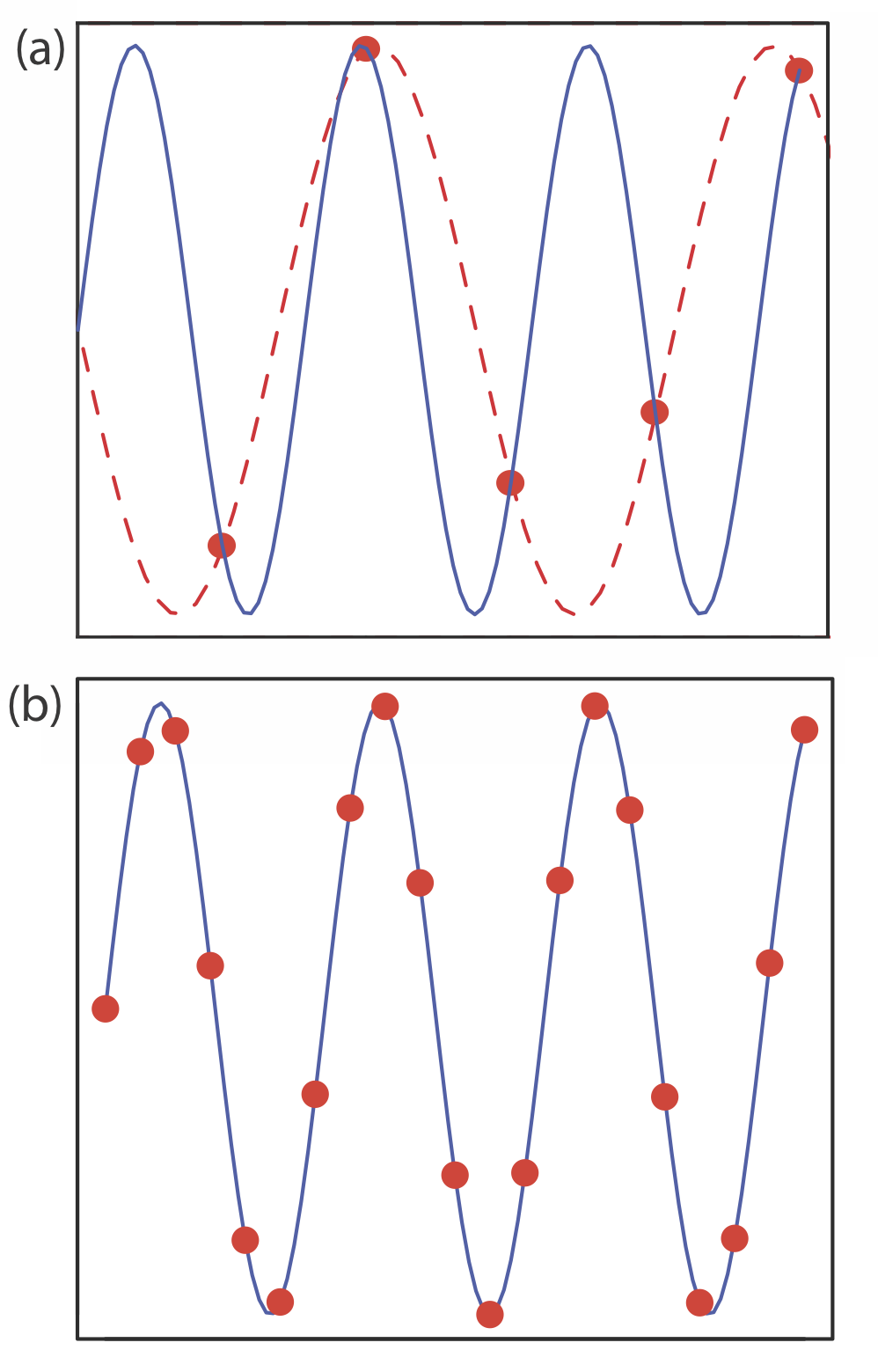
Según el teorema de Nyquist, para determinar con precisión la frecuencia de una señal periódica, debemos muestrear la señal al menos dos veces durante cada ciclo o periodo. Si recolectamos muestras en un intervalo de\(\Delta t\), entonces la frecuencia más alta que podemos monitorear con precisión es\((2 \Delta t)^{-1}\). Por ejemplo, si recolectamos una muestra cada hora, entonces la frecuencia más alta que podemos monitorear es (2\(\times\) 1 hr) ^—1 o 0.5 hr ^—1, un periodo de menos de 2 hr. Si el periodo de nuestra señal es inferior a 2 horas (una frecuencia de más de 0.5 hr ^—1), entonces debemos usar una frecuencia de muestreo más rápida. Idealmente, utilizamos una frecuencia de muestreo que es al menos 3—4 veces mayor que la señal de frecuencia más alta de interés. Si nuestra señal tiene un periodo de una hora, entonces debemos recolectar una nueva muestra cada 15-20 minutos.

Muestreo Sistemático-Juzgado

También son posibles combinaciones de los tres enfoques primarios para el muestreo [Keith, L. H. Environ. Sci. Tecnol. 1990, 24, 610—617]. Una de esas combinaciones es el muestreo sistemático-juicioso, en el que utilizamos conocimientos previos sobre un sistema para guiar un plan de muestreo sistemático. Por ejemplo, al monitorear la lixiviación de desechos de un relleno sanitario, esperamos que el penacho se mueva en la misma dirección que el flujo de las aguas subterráneas, esto ayuda a enfocar nuestro muestreo, ahorrando dinero y tiempo. El plan de muestreo sistemático-juicioso en la Figura 7.2.3 incluye una cuadrícula rectangular para la mayoría de las muestras y transectos lineales para explorar los límites del penacho [Flatman, G. T.; Englund, E. J.; Yfantis, A. A. en Keith, L. H., ed. Principles of Environmental Sampling, American Chemical Society: Washington, D. C., 1988, 73—84].

Figura 7.2.3 . Plan de muestreo sistemático-crítico para monitorear la lixiviación de contaminantes de un relleno sanitario. Los sitios de muestreo, mostrados como puntos rojos, se encuentran en una rejilla sistemática que se traslada a ambos lados de la dirección del flujo del agua subterránea. El muestreo a lo largo de los transectos lineales que se extienden desde la cuadrícula ayuda a establecer los límites de la pluma.

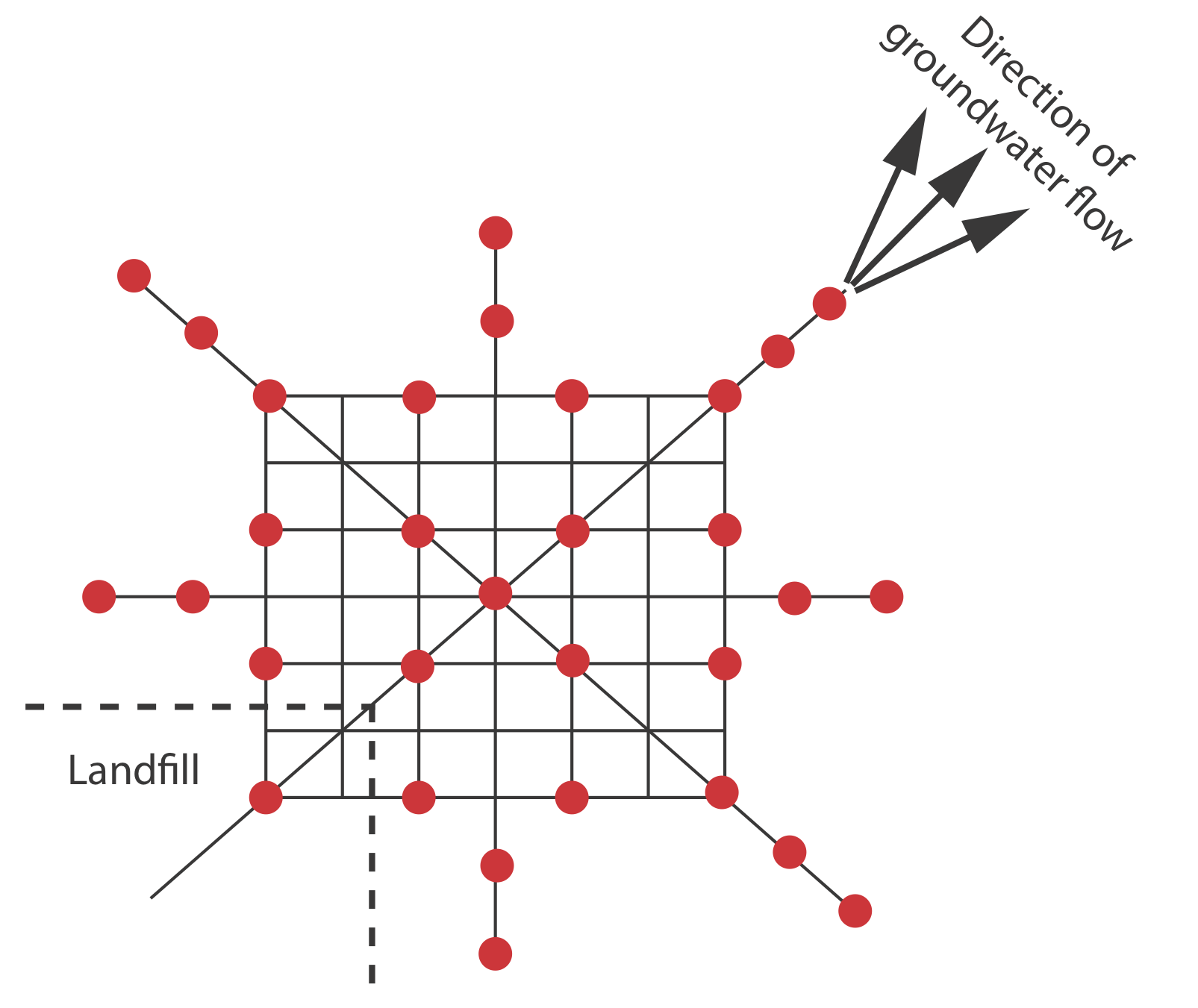
Muestreo estratificado

Otra combinación de los tres enfoques primarios para el muestreo es el muestreo juicial-aleatorio o estratificado. Muchas poblaciones objetivo consisten en distintas unidades o estratos. Por ejemplo, supongamos que estamos estudiando Pb particulado en el aire urbano. Debido a que las partículas vienen en una variedad de tamaños, algunas visibles y otras microscópicas, y provienen de muchas fuentes, como polvo de carretera, hollín diesel y cenizas volantes, por nombrar algunas, podemos subdividir la población objetivo por tamaño o por fuente. Si elegimos un plan de muestreo aleatorio, entonces recolectamos muestras sin considerar los diferentes estratos, lo que puede sesgar la muestra hacia partículas más grandes. En un muestreo estratificado dividimos la población objetivo en estratos y recolectamos muestras aleatorias dentro de cada estrato. Después de analizar las muestras de cada estrato, agrupamos sus respectivas medias para dar una media global para la población objetivo. La ventaja del muestreo estratificado es que los estratos individuales suelen ser más homogéneos que la población objetivo. La varianza general del muestreo para el muestreo estratificado siempre es al menos igual de buena, y a menudo es mejor que la obtenida por muestreo aleatorio simple. Debido a que un muestreo estratificado requiere que recolectemos y analicemos muestras de varios estratos, a menudo requiere más tiempo y dinero.

Muestreo Conveniente

Un método adicional de muestreo merece ser mencionado. En el muestreo de conveniencia seleccionamos sitios de muestreo utilizando criterios distintos de minimizar el error de muestreo y la varianza de muestreo. En un estudio de la calidad del agua subterránea rural, por ejemplo, podemos optar por perforar pozos en sitios seleccionados al azar o podemos optar por aprovechar los pozos existentes; este último suele ser la opción preferida. En este caso, el costo, la conveniencia y la accesibilidad son más importantes que garantizar una muestra aleatoria

Qué Tipo de Muestra Recoger

Habiendo determinado desde dónde recolectar las muestras, el siguiente paso en el diseño de un plan de muestreo es decidir el tipo de muestra a recolectar. Existen tres métodos comunes para la obtención de muestras: toma de muestras, muestreo compuesto y muestreo in situ.

El tipo de muestra más común es una muestra de captura en la que recolectamos una porción de la población objetivo en un momento o lugar específicos, proporcionando una “instantánea” de la población objetivo. Si nuestra población objetivo es homogénea, una serie de muestras aleatorias de captura nos permite establecer sus propiedades. Para una población objetivo heterogénea, el muestreo sistemático de captura permite caracterizar cómo cambian sus propiedades a lo largo del tiempo y/o el espacio.

Una muestra compuesta es un conjunto de muestras de agarre que combinamos en una sola muestra antes del análisis. Debido a que la información se pierde cuando combinamos muestras individuales, normalmente analizamos por separado cada muestra de captura. En algunas situaciones, sin embargo, hay ventajas al trabajar con una muestra compuesta.

Una situación en la que el muestreo compuesto es apropiado es cuando nuestro interés está en la composición promedio de la población objetivo a lo largo del tiempo o el espacio. Por ejemplo, las plantas de tratamiento de aguas residuales deben monitorear y reportar la composición diaria promedio del agua tratada que liberan al ambiente. El analista puede recopilar y analizar un conjunto de muestras individuales de captura y reportar el resultado promedio, o puede ahorrar tiempo y dinero combinando las muestras de captura en una sola muestra compuesta y reportar el resultado de su análisis de la muestra compuesta.

El muestreo compuesto también es útil cuando una sola muestra no suministra suficiente material para el análisis. Por ejemplo, los métodos analíticos para el análisis cuantitativo de PCB en peces a menudo requieren hasta 50 g de tejido, cantidad que puede ser difícil de obtener de un solo pez. Combinar y homogeneizar muestras de tejido de varios peces facilita la obtención de la muestra de 50 g necesaria.

Una desventaja significativa de las muestras de captura y las muestras compuestas es que no podemos utilizarlas para monitorear continuamente un cambio dependiente del tiempo en la población objetivo. El muestreo in situ, en el que insertamos un sensor analítico en la población objetivo, nos permite monitorear la población objetivo sin retirar muestras individuales de captura. Por ejemplo, podemos monitorear el pH de una solución en una línea de producción industrial sumergiendo un electrodo de pH en el flujo de la solución.

Ejemplo 7.2.2

Un estudio de la relación entre la densidad de tráfico y las concentraciones de Pb, Cd y Zn en suelos de carretera utiliza el siguiente plan de muestreo [Nabulo, G.; Oryem-Origa, H.; Diamond, M. Environ. Res. 2006, 101, 42—52]. Se recolectan muestras de suelo superficial (0—10 cm) a distancias de 1, 5, 10, 20 y 30 m de la carretera. A cada distancia, se toman 10 muestras de diferentes localizaciones y se mezclan para formar una sola muestra. ¿Qué tipo de plan de muestreo es este? Explique por qué se trata de un plan de muestreo adecuado.

Solución

Se trata de un plan de muestreo sistemático-decisivo que utiliza muestras compuestas. Estas son buenas elecciones dadas las metas del estudio. Las emisiones de automóviles liberan partículas que contienen concentraciones elevadas de Pb, Cd y ZN, este estudio se realizó en Uganda, donde todavía se usaba gasolina con plomo, que se asientan en los suelos circundantes de la carretera como “lluvia seca”. Las muestras recolectadas cerca de la carretera y las muestras recolectadas a distancias fijas de la carretera proporcionan datos suficientes para el estudio, al tiempo que minimizan el número total de muestras. Combinar muestras de la misma distancia en una sola muestra compuesta tiene la ventaja de disminuir la incertidumbre del muestreo.

Cuánta muestra recolectar

Para minimizar los errores de muestreo, las muestras deben ser de un tamaño apropiado. Si una muestra es demasiado pequeña su composición puede diferir sustancialmente de la de la población objetivo, lo que introduce un error de muestreo. Muestras que son demasiado grandes, sin embargo, requieren más tiempo y dinero para recolectar y analizar, sin proporcionar una mejora significativa en el error de muestreo.

Supongamos que nuestra población objetivo es una mezcla homogénea de dos tipos de partículas. Las partículas de tipo A contienen una concentración fija de analito y las partículas de tipo B están libres de analito. Las muestras de esta población objetivo siguen una distribución binomial. Si recolectamos una muestra de n partículas, entonces el número esperado de partículas que contiene analito, n _A, es

\[n_{A}=n p \nonumber\]

donde p es la probabilidad de seleccionar una partícula de tipo A. La desviación estándar para el muestreo es

\[s_{samp}=\sqrt{n p(1-p)} \label{7.1}\]

Para calcular la desviación estándar relativa para el muestreo,\(\left( s_{samp} \right)_{rel}\), dividimos la Ecuación\ ref {7.1} por n _A, obteniendo

\[\left(s_{samp}\right)_{r e l}=\frac{\sqrt{n p(1-p)}}{n p} \nonumber\]

Resolver para n nos permite calcular el número de partículas que necesitamos para proporcionar una varianza de muestreo relativa deseada.

\[n=\frac{1-p}{p} \times \frac{1}{\left(s_{s a m p}\right)_{rel}^{2}} \label{7.2}\]

Ejemplo 7.2.3

Supongamos que estamos analizando un suelo donde las partículas que contienen analito representan solo\(1 \times 10^{-7}\)% de la población. ¿Cuántas partículas debemos recolectar para dar un porcentaje de desviación estándar relativa para el muestreo de 1%?

Solución

Dado que las partículas de interés representan\(1 \times 10^{-7}\)% de todas las partículas, la probabilidad, p, de seleccionar una de estas partículas es\(1 \times 10^{-9}\). Sustituyendo en Ecuación\ ref {7.2} da

\[n=\frac{1-\left(1 \times 10^{-9}\right)}{1 \times 10^{-9}} \times \frac{1}{(0.01)^{2}}=1 \times 10^{13} \nonumber\]

Para obtener una desviación estándar relativa para el muestreo de 1%, necesitamos recolectar\(1 \times 10^{13}\) partículas.

Dependiendo del tamaño de partícula, una muestra de 10 ¹³ partículas puede ser bastante grande. Supongamos que esto equivale a una masa de 80 g. Trabajar con una muestra tan grande claramente no es práctico. ¿Significa esto que debemos trabajar con una muestra más pequeña y aceptar una desviación estándar relativa mayor para el muestreo? Afortunadamente la respuesta es no. Una característica importante de la Ecuación\ ref {7.2} es que la desviación estándar relativa para el muestreo es una función del número de partículas en lugar de su masa combinada. Si trituramos y trituramos las partículas para hacerlas más pequeñas, entonces una muestra de 10 ¹³ partículas tendrá una masa menor. Si asumimos que una partícula es esférica, entonces su masa es proporcional al cubo de su radio.

\[\operatorname{mass} \propto r^{3} \nonumber\]

Si disminuimos el radio de una partícula en un factor de 2, por ejemplo, entonces disminuimos su masa en un factor de 2 ³, u 8. Esto supone, por supuesto, que el proceso de trituración y molienda de partículas no cambia la composición de las partículas.

Ejemplo 7.2.4

Supongamos que una muestra de 10 ¹³ partículas del Ejemplo 7.2.3 pesa 80 g y que las partículas son esféricas. ¿En cuánto debemos reducir el radio de una partícula si queremos trabajar con muestras de 0.6-g?

Solución

Para reducir la masa de la muestra de 80 g a 0.6 g, debemos cambiar su masa por un factor de

\[\frac{80}{0.6}=133 \times \nonumber\]

Para lograr esto debemos disminuir el radio de una partícula en un factor de

\[\begin{aligned} r^{3} &=133 \times \\ r &=5.1 \times \end{aligned} \nonumber\]

Disminuir el radio por un factor de aproximadamente 5 permite disminuir la masa de la muestra de 80 g a 0.6 g.

Tratar a una población como si solo contenga dos tipos de partículas es un ejercicio útil porque nos muestra que podemos mejorar la desviación estándar relativa para el muestreo recolectando más partículas. Por supuesto, una población real probablemente contenga más de dos tipos de partículas, con el analito presente en varios niveles de concentración. Sin embargo, el muestreo de muchas poblaciones bien mezcladas se aproxima a las estadísticas de muestreo binomial porque son homogéneas en la escala a la que se muestrean. En estas condiciones, la siguiente relación entre la masa de una muestra aleatoria de captura, m, y el porcentaje de desviación estándar relativa para el muestreo, R, a menudo es válida

\[m R^{2}=K_{s} \label{7.3}\]

donde K _s es una constante de muestreo igual a la masa de una muestra que produce un porcentaje de desviación estándar relativa para el muestreo de ± 1% [Ingamells, C. O.; Switzer, P. Talanta 1973, 20, 547—568].

Ejemplo 7.2.5

Los siguientes datos se obtuvieron en una determinación preliminar de la cantidad de cenizas inorgánicas en un cereal de desayuno.

masa de cereal (g)	0.9956	0.9981	1.0036	0.9994	1.0067
%w/w de ceniza	1.34	1.29	1.32	1.26	1.28

Cuál es el valor de K _s y qué tamaño de muestra se necesita para dar un porcentaje de desviación estándar relativa para el muestreo de ± 2.0%. Predecir el porcentaje de desviación estándar relativa y la desviación estándar absoluta si recolectamos muestras de 5.00-g.

Solución

Para determinar la constante de muestreo, K _s, necesitamos conocer la masa promedio de las muestras de cereal y la desviación estándar relativa para la cantidad de cenizas en esas muestras. La masa promedio de las muestras de cereales es de 1.0007 g. El% w/w de cenizas promedio y su desviación estándar absoluta son, respectivamente, 1.298%w/w y 0.03194 %w/w. La desviación estándar relativa porcentual, R, por lo tanto, es

\[R=\frac{s_{\text { samp }}}{\overline{X}}=\frac{0.03194 \% \ \mathrm{w} / \mathrm{w}}{1.298 \% \ \mathrm{w} / \mathrm{w}} \times 100=2.46 \% \nonumber\]

Resolver para K _s da su valor como

\[K_{s}=m R^{2}=(1.0007 \mathrm{g})(2.46)^{2}=6.06 \ \mathrm{g} \nonumber\]

Para obtener un porcentaje de desviación estándar relativa de ± 2%, las muestras deben tener una masa de al menos

\[m=\frac{K_{s}}{R^{2}}=\frac{6.06 \mathrm{g}}{(2.0)^{2}}=1.5 \ \mathrm{g} \nonumber\]

Si utilizamos muestras de 5.00-g, entonces la desviación estándar relativa porcentual esperada es

\[R=\sqrt{\frac{K_{s}}{m}}=\sqrt{\frac{6.06 \mathrm{g}}{5.00 \mathrm{g}}}=1.10 \% \nonumber\]

y la desviación estándar absoluta esperada es

\[s_{\text { samp }}=\frac{R \overline{X}}{100}=\frac{(1.10)(1.298 \% \mathrm{w} / \mathrm{w})}{100}=0.0143 \% \mathrm{w} / \mathrm{w} \nonumber\]

Ejercicio 7.2.1

Olaquindox es un promotor sintético del crecimiento en alimentos medicados para cerdos. En un análisis de un lote de producción de pienso, se recolectaron y analizaron cinco muestras con masas nominales de 0.95 g, con los resultados mostrados en la siguiente tabla.

masa (g)	0.9530	0.9728	0.9660	0.9402	0.9576
mg olaquindox/kg pienso	23.0	23.8	21.0	26.5	21.4

¿Cuál es el valor de K _s y qué tamaño se necesitan muestras para obtener una desviación relativa porcentual para el muestreo de 5.0%? ¿Por cuánto se necesita para reducir el tamaño promedio de partícula si las muestras no deben pesar más de 1 g?

Contestar

Para determinar la constante de muestreo, K _s, necesitamos conocer la masa promedio de las muestras y el porcentaje de desviación estándar relativa para la concentración de olaquindox en el alimento. La masa promedio para las cinco muestras es de 0.95792 g, la concentración promedio de olaquindox en las muestras es de 23.14 mg/kg con una desviación estándar de 2.200 mg/kg. El porcentaje de desviación estándar relativa, R, es

\[R=\frac{s_{\text { samp }}}{\overline{X}} \times 100=\frac{2.200 \ \mathrm{mg} / \mathrm{kg}}{23.14 \ \mathrm{mg} / \mathrm{kg}} \times 100=9.507 \approx 9.51 \nonumber\]

Resolver para K _s da su valor como

\[K_{s}=m R^{2}=(0.95792 \mathrm{g})(9.507)^{2}=86.58 \ \mathrm{g} \approx 86.6 \ \mathrm{g} \nonumber\]

Para obtener una desviación estándar relativa porcentual de 5.0%, las muestras individuales necesitan tener una masa de al menos

\[m=\frac{K_{s}}{R^{2}}=\frac{86.58 \ \mathrm{g}}{(5.0)^{2}}=3.5 \ \mathrm{g} \nonumber\]

Para reducir la masa de la muestra de 3.5 g a 1 g, debemos cambiar la masa por un factor de

\[\frac{3.5 \ \mathrm{g}}{1 \ \mathrm{g}}=3.5 \times \nonumber\]

Si asumimos que las partículas de la muestra son esféricas, entonces debemos reducir el radio de una partícula en un factor de

\[\begin{aligned} r^{3} &=3.5 \times \\ r &=1.5 \times \end{aligned} \nonumber\]

Cuántas muestras recoger

En la sección anterior se consideró cuánta muestra necesitamos para minimizar la desviación estándar debida al muestreo. Otra consideración importante es el número de muestras a recolectar. Si los resultados de nuestro análisis de las muestras se distribuyen normalmente, entonces el intervalo de confianza para el error de muestreo es

\[\mu=\overline{X} \pm \frac{t s_{samp}}{\sqrt{n_{samp}}} \label{7.4}\]

donde n _samp es el número de muestras y s _samp es la desviación estándar para el muestreo. Reordenando la ecuación\ ref {7.4} y sustituyendo e por la cantidad\(\overline{X} - \mu\), da el número de muestras como

\[n_{samp}=\frac{t^{2} s_{samp}^{2}}{e^{2}} \label{7.5}\]

Debido a que el valor de t depende de n _samp, la solución a la Ecuación\ ref {7.5} se encuentra iterativamente.

Cuando usamos la Ecuación\ ref {7.5}, debemos expresar la desviación estándar para el muestreo, s _samp, y el error, e, de la misma manera. Si s _samp se reporta como porcentaje de desviación estándar relativa, entonces el error, e, se reporta como un porcentaje de error relativo. Cuando uses Ecuación\ ref {7.5}, asegúrate de verificar que estás expresando s _samp y e de la misma manera.

Ejemplo 7.2.6

En Ejemplo {{template.index (ID:5)} determinamos que necesitamos muestras de 1.5-g para establecer una s _samp de ± 2.0% para la cantidad de ceniza inorgánica en cereal. ¿Cuántas muestras de 1.5 g necesitamos recolectar para obtener un porcentaje de error de muestreo relativo de ± 0.80% al nivel de confianza del 95%?

Solución

Debido a que el valor de t depende del número de muestras, un resultado que aún tenemos que calcular, comenzamos dejando n _samp =\(\infty\) y usando t (0.05,\(\infty\)) para t. Del Apéndice 4, el valor para t (0.05,\(\infty\)) es 1.960. Sustituir valores conocidos en la ecuación\ ref {7.5} da el número de muestras como

\[n_{samp}=\frac{(1.960)^{2}(2.0)^{2}}{(0.80)^{2}}=24.0 \approx 24 \nonumber\]

Dejando n _samp = 24, el valor de t (0.05, 23) del Apéndice 4 es 2.073. Recalculando n _samp da

\[n_{samp}=\frac{(2.073)^{2}(2.0)^{2}}{(0.80)^{2}}=26.9 \approx 27 \nonumber\]

Cuando n _samp = 27, el valor de t (0.05, 26) del Apéndice 4 es 2.060. Recalculando n _samp da

\[n_{samp}=\frac{(2.060)^{2}(2.0)^{2}}{(0.80)^{2}}=26.52 \approx 27 \nonumber\]

Debido a que dos cálculos sucesivos dan el mismo valor para n _samp, tenemos una solución iterativa al problema. Se necesitan 27 muestras para lograr un porcentaje de error de muestreo relativo de ± 0.80% al nivel de confianza del 95%.

Ejercicio 7.2.2

Suponiendo que el porcentaje de desviación estándar relativa para el muestreo en la determinación de olaquindox en pienso medicado es de 5.0% (ver Ejercicio 7.2.1 ), ¿cuántas muestras necesitamos analizar para obtener un porcentaje de error relativo de muestreo de ± 2.5% a\(\alpha\) = 0.05?

Contestar

Debido a que el valor de t depende del número de muestras, un resultado que aún tenemos que calcular, comenzamos dejando n _samp =\(\infty\) y usando t (0.05,\(\infty\)) para el valor de t. Del Apéndice 4, el valor para t (0.05,\(\infty\)) es 1.960. Nuestra primera estimación para n _samp es

\[n_{samp}=\frac{t^{2} s_{s a m p}^{2}}{e^{2}} = \frac{(1.96)^{2}(5.0)^{2}}{(2.5)^{2}}=15.4 \approx 15 \nonumber\]

Dejando n _samp = 15, el valor de t (0.05,14) del Apéndice 4 es 2.145. Recalculando n _samp da

\[n_{samp}=\frac{t^{2} s_{samp}^{2}}{e^{2}}=\frac{(2.145)^{2}(5.0)^{2}}{(2.5)^{2}}=18.4 \approx 18 \nonumber\]

Dejando n _samp = 18, el valor de t (0.05,17) del Apéndice 4 es 2.103. Recalculando n _samp da

\[n_{samp}=\frac{t^{2} s_{samp}^{2}}{e^{2}}=\frac{(2.103)^{2}(5.0)^{2}}{(2.5)^{2}}=17.7 \approx 18 \nonumber\]

Debido a que dos cálculos sucesivos dan el mismo valor para n _samp, necesitamos 18 muestras para lograr un error de muestreo de ± 2.5% en el intervalo de confianza del 95%.

La ecuación\ ref {7.5} proporciona una estimación para el menor número de muestras que producirá el error de muestreo deseado. El error real de muestreo puede ser sustancialmente mayor si s _samp para las muestras que recolectamos durante el análisis posterior es mayor que s _samp utilizado para calcular n _samp . Este no es un problema infrecuente. Para una población objetivo con una varianza de muestreo relativa de 50 y un error de muestreo relativo deseado de ± 5%, la Ecuación\ ref {7.5} predice que 10 muestras son suficientes. En una simulación que utilizó 1000 muestras de tamaño 10, sin embargo, solo 57% de los ensayos resultaron en un error de muestreo de menos de ± 5% [Blackwood, L. G. Environ. Sci. Tecnol. 1991, 25, 1366—1367]. Aumentar el número de muestras a 17 fue suficiente para asegurar que el error de muestreo deseado se logró 95% del tiempo.

Para una interesante discusión de por qué es importante el número de muestras, ver Kaplan, D.; Lacetera, N.; Kaplan, C. “Tamaño de la muestra y precisión en NIH Peer Review”, Plos One, 2008, 3 (7), 1—3. Al revisar las subvenciones, los revisores individuales reportan una puntuación entre 1.0 y 5.0 (dos cifras significativas). El NIH reporta el puntaje promedio a tres cifras significativas, lo que implica que una diferencia de 0.01 es significativa. Si las puntuaciones individuales tienen una desviación estándar de 0.1, entonces una diferencia de 0.01 es significativa en\(\alpha = 0.05\) sólo si hay 384 revisiones. Los autores concluyen que los paneles de revisión de los NIH son demasiado pequeños para proporcionar una separación estadísticamente significativa entre las propuestas que reciben puntuaciones similares.

Minimizar la varianza general

Una consideración final cuando desarrollamos un plan de muestreo es cómo podemos minimizar la varianza general para el análisis. La ecuación 7.1.2 muestra que la varianza global es una función de la varianza debida al método\(s_{meth}^2\), y la varianza debida al muestreo,\(s_{samp}^2\). Como aprendimos anteriormente, podemos mejorar la varianza de muestreo recolectando más muestras del tamaño adecuado. Aumentar el número de veces que analizamos cada muestra mejora la varianza del método. Si\(s_{samp}^2\) es significativamente mayor que\(s_{meth}^2\), podemos ignorar la contribución del método a la varianza general y usar la Ecuación\ ref {7.5} para estimar el número de muestras a analizar. Analizar cualquier muestra más de una vez no mejorará la varianza general, ya que la varianza del método es insignificante.

Si\(s_{meth}^2\) es significativamente mayor que\(s_{samp}^2\), entonces necesitamos recolectar y analizar solo una muestra. El número de análisis replicados, n _rep, que necesitamos para minimizar el error debido al método viene dado por una ecuación similar a la Ecuación\ ref {7.5}.

\[n_{rep}=\frac{t^{2} s_{m e t h}^{2}}{e^{2}} \nonumber\]

Desafortunadamente, las situaciones simples descritas anteriormente a menudo son la excepción. Para muchos análisis, tanto la varianza de muestreo como la varianza del método son significativas, y son necesarios tanto múltiples muestras como análisis replicados de cada muestra. El error general en este caso es

\[e=t \sqrt{\frac{s_{samp}^{2}}{n_{samp}} + \frac{s_{meth}^{2}}{n_{sam p} n_{rep}}} \label{7.6}\]

La ecuación\ ref {7.6} no tiene una solución única ya que diferentes combinaciones de n _samp y n _rep dan el mismo error general. La cantidad de muestras que recolectamos y cuántas veces analizamos cada muestra está determinada por otras preocupaciones, como el costo de recolectar y analizar muestras, y la cantidad de muestra disponible.

Ejemplo 7.2.7

Un método analítico tiene una varianza de muestreo relativa de 0.40% y una varianza de método relativo de 0.070%. Evalúa el porcentaje de error relativo (\(\alpha = 0.05\)) si recolectas 5 muestras y analizas cada una dos veces, y si recolectas 2 muestras y analizas cada 5 veces.

Solución

Ambas estrategias de muestreo requieren un total de 10 análisis. Del Apéndice 4 encontramos que el valor de t (0.05, 9) es 2.262. Usando la ecuación\ ref {7.6}, el error relativo para la primera estrategia de muestreo es

\[e=2.262 \sqrt{\frac{0.40}{5}+\frac{0.070}{5 \times 2}}=0.67 \% \nonumber\]

y que para la segunda estrategia de muestreo es

\[e=2.262 \sqrt{\frac{0.40}{2}+\frac{0.070}{2 \times 5}}=1.0 \% \nonumber\]

Debido a que la varianza del método es menor que la varianza de muestreo, obtenemos un error relativo menor si recolectamos más muestras y analizamos cada muestra menos veces.

Ejercicio 7.2.3

Un método analítico tiene una varianza de muestreo relativa de 0.10% y una varianza de método relativo de 0.20%. El costo de recolectar una muestra es de $20 y el costo de analizar una muestra es de $50. Proponer una estrategia de muestreo que proporcione un error relativo máximo de ± 0.50% (\(\alpha = 0.05\)) y un costo máximo de $700.

Contestar

Si recolectamos una sola muestra (costo $20), entonces podemos analizar esa muestra 13 veces (costo $650) y mantenernos dentro de nuestro presupuesto. Para este escenario, el porcentaje de error relativo es

\[e=t \sqrt{\frac{s_{samp}^{2}}{n_{samp}} + \frac{s_{meth}^{2}}{n_{sam p} n_{rep}}} = 2.179 \sqrt{\frac{0.10}{1}+\frac{0.20}{1 \times 13}}=0.74 \% \nonumber\]

donde t (0.05, 12) es 2.179. Debido a que este porcentaje de error relativo es mayor a ± 0.50%, esta no es una estrategia de muestreo adecuada.

A continuación, probamos dos muestras (costo $40), analizando cada seis veces (costo $600). Para este escenario, el porcentaje de error relativo es

\[e=t \sqrt{\frac{s_{samp}^{2}}{n_{samp}} + \frac{s_{meth}^{2}}{n_{sam p} n_{rep}}} = 2.2035 \sqrt{\frac{0.10}{2}+\frac{0.20}{2 \times 6}}=0.57 \% \nonumber\]

donde t (0.05, 11) es 2.2035. Debido a que este porcentaje de error relativo es mayor a ± 0.50%, esta tampoco es una estrategia de muestreo adecuada.

A continuación probamos tres muestras (costo $60), analizando cada cuatro veces (costo $600). Para este escenario, el porcentaje de error relativo es

\[e=t \sqrt{\frac{s_{samp}^{2}}{n_{samp}} + \frac{s_{meth}^{2}}{n_{sam p} n_{rep}}} = 2.2035 \sqrt{\frac{0.10}{3}+\frac{0.20}{3 \times 4}}=0.49 \% \nonumber\]

donde t (0.05, 11) es 2.2035. Debido a que tanto el costo total ($660) como el porcentaje de error relativo cumplen con nuestros requisitos, esta es una estrategia de muestreo adecuada.

Existen otras estrategias de muestreo adecuadas que cumplen ambos objetivos. La estrategia que menos gasto requiere es recolectar ocho muestras, analizando cada una una una por un costo total de $560 y un porcentaje de error relativo de ± 0.46%. Recolectar 10 muestras y analizarlas cada vez, da un porcentaje de error relativo de ± 0.39% a un costo de $700.