10.8: Espectroscopia basada en dispersión
- Page ID
- 75888
El color azul del cielo durante el día y el rojo del sol al atardecer son el resultado de la luz dispersada por pequeñas partículas de polvo, moléculas de agua y otros gases en la atmósfera. La eficiencia de la dispersión de un fotón depende de su longitud de onda. Vemos el cielo como azul durante el día porque la luz violeta y azul se dispersan en mayor medida que otras longitudes de onda de luz más largas. Por la misma razón, el sol aparece rojo al atardecer porque la luz roja se dispersa de manera menos eficiente y es más probable que pase a través de la atmósfera que otras longitudes de onda de luz. La dispersión de la radiación se ha estudiado desde finales del siglo XIX, con aplicaciones que comienzan poco después. Las primeras aplicaciones cuantitativas de dispersión, que datan de principios del siglo XX, utilizaron la dispersión elástica de la luz por suspensiones coloidales para determinar la concentración de partículas coloidales.
Origen de la dispersión
Si enviamos un haz de radiación focalizado y monocromático con una longitud de onda\(\lambda\) a través de un medio de partículas con dimensiones\(< 1.5 \lambda\), la radiación se dispersa en todas las direcciones. Por ejemplo, la radiación visible de 500 nm es dispersada por partículas de hasta 750 nm en la dimensión más larga. Se reconocen dos categorías generales de dispersión. En la dispersión elástica, la radiación es absorbida primero por las partículas y luego emitida sin sufrir un cambio en la energía de la radiación. Cuando la radiación emerge con un cambio de energía, la dispersión es inelástica. En este texto sólo se considera la dispersión elástica.
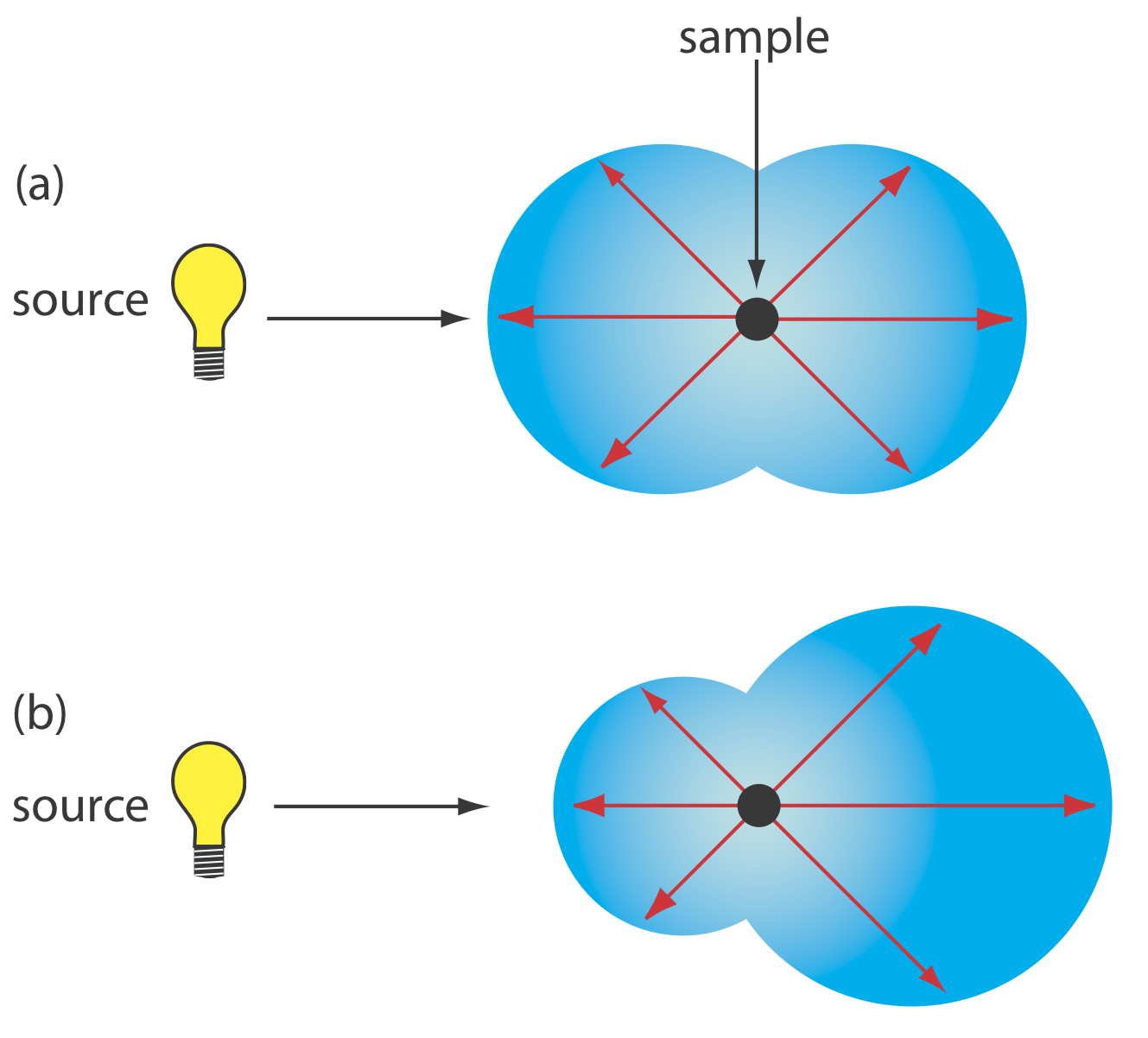
La dispersión elástica se divide en dos tipos: Rayleigh, o dispersión de partículas pequeñas, y dispersión de partículas grandes. La dispersión de Rayleigh ocurre cuando la dimensión más grande de la partícula de dispersión es inferior al 5% de la longitud de onda de la radiación. La intensidad de la radiación dispersa es proporcional a su frecuencia a la cuarta potencia,\(\nu^4\) lo que explica la mayor dispersión de la luz azul que la luz roja, y se distribuye simétricamente (Figura 10.8.1 a). Para partículas más grandes, la dispersión aumenta en la dirección hacia adelante y disminuye en la dirección hacia atrás como resultado de interferencias constructivas y destructivas (Figura 10.8.1 b).
Turbidimetría y nefelometría
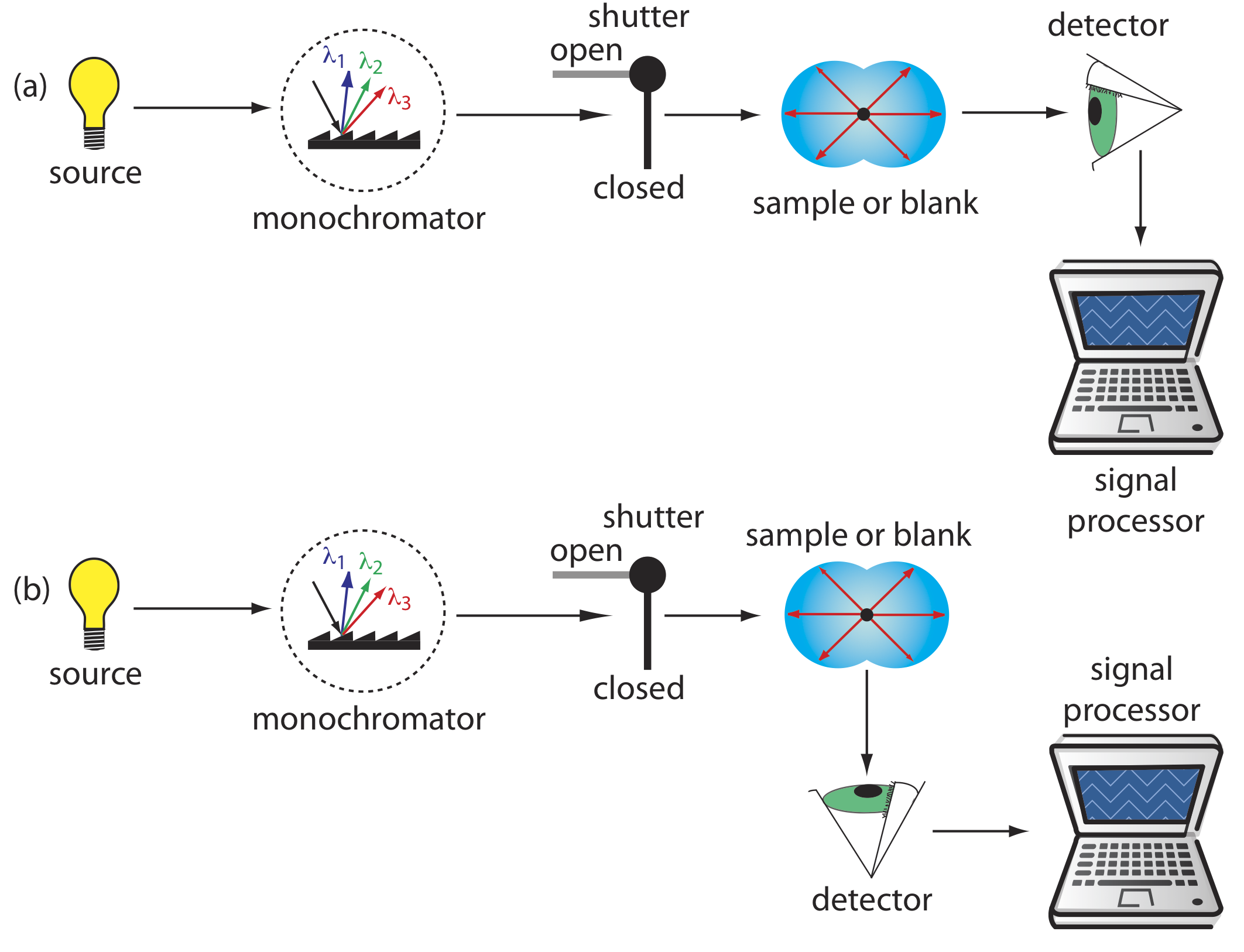
La turbidimetría y la nefelometría son dos técnicas que se basan en la dispersión elástica de la radiación por una suspensión de partículas coloidales. En turbidimetría el detector se coloca en línea con la fuente y se mide la disminución en la potencia transmitida de la radiación. En nefelometría la radiación dispersa se mide en un ángulo de 90 o con respecto a la fuente. La similitud de la turbidimetría con la espectroscopia de absorbancia y de la nefelometría con la espectroscopia de fluorescencia es evidente en los diseños instrumentales mostrados en la Figura 10.8.2 . De hecho, podemos usar un espectrofotómetro UV/Vis para turbidimetría y podemos usar un espectrofluorómetro para nefelometría.
¿Turbidimetría o Nefelometría?
Al desarrollar un método de dispersión, la elección entre usar turbidimetría o usar nefelometría se determina por dos factores. La consideración más importante es la intensidad de la radiación dispersa en relación con la intensidad de la radiación de la fuente. Si la solución contiene una pequeña concentración de partículas dispersantes, entonces la intensidad de la radiación transmitida, I T, es aproximadamente la misma que la intensidad de la radiación de la fuente, I 0. Como aprendimos anteriormente en la sección sobre absorción molecular, existe una incertidumbre sustancial en la determinación de una pequeña diferencia entre dos señales intensas. Por esta razón, la nefelometría es una opción más apropiada para una muestra que contiene pocas partículas dispersantes. La turbidimetría es una mejor opción cuando la muestra contiene una alta concentración de partículas dispersantes.
Una segunda consideración al elegir entre turbidimetría y nefelometría es el tamaño de las partículas dispersantes. Para la nefelometría, la intensidad de la radiación dispersa a 90 o aumenta cuando las partículas son pequeñas y la dispersión de Rayleigh está en efecto. Para partículas más grandes, como se muestra en la Figura 10.8.1 , la intensidad de dispersión disminuye a 90 o. Cuando se usa una fuente de radiación ultravioleta o visible, el tamaño óptimo de partícula es 0.1—1 μm. El tamaño de las partículas de dispersión es menos importante para la turbidimetría donde la señal es la disminución relativa de la radiación transmitida. De hecho, las mediciones turbidimétricas son factibles incluso cuando el tamaño de las partículas de dispersión da como resultado un aumento en la reflexión y refracción, aunque una relación lineal entre la señal y la concentración de partículas dispersantes puede que ya no se mantenga.
Determinación de la concentración por turbidimetría
Para la turbidimetría la transmitancia medida, T, es la relación de la intensidad de la radiación fuente transmitida por la muestra, I T, a la intensidad de la radiación fuente transmitida por un blanco, I 0.
\[T=\frac{I_{\mathrm{T}}}{I_{0}} \nonumber\]
La relación entre la transmitancia y la concentración de las partículas dispersantes es similar a la dada por la ley de Beer
\[-\log T=k b C \label{10.1}\]
donde C es la concentración de las partículas dispersantes en masa por unidad de volumen (p/v), b es la longitud de la trayectoria y k es una constante que depende de varios factores, incluyendo el tamaño y la forma de las partículas de dispersión y la longitud de onda de la radiación fuente. La relación exacta se establece mediante una curva de calibración preparada usando una serie de estándares que contienen concentraciones conocidas de analito. Al igual que con la ley de Beer, la Ecuación\ ref {10.1} puede mostrar desviaciones apreciables de la linealidad.
Determinación de la Concentración por Nefelometría
Para la nefelometría la relación entre la intensidad de la radiación dispersa, I S, y la concentración de partículas dispersantes es
\[I_{\mathrm{s}}=k I_{0} C \label{10.2}\]
donde k es una constante empírica para el sistema e I 0 es la intensidad de la radiación fuente. El valor de k se determina a partir de una curva de calibración preparada usando una serie de patrones que contienen concentraciones conocidas de analito.
Selección de una longitud de onda para la radiación incidente
La elección de la longitud de onda se basa principalmente en la necesidad de minimizar las interferencias potenciales. Para la turbidimetría, donde la radiación incidente se transmite a través de la muestra, un monocromador o filtro nos permite evitar longitudes de onda que son absorbidas en lugar de dispersarse por la muestra. Para la nefelometría, la absorción de radiación incidente no es un problema a menos que induzca fluorescencia de la muestra. Con una muestra no fluorescente no hay necesidad de selección de longitud de onda y se puede utilizar una fuente de luz blanca como radiación incidente. Para ambas técnicas, otras consideraciones al elegir una longitud de onda incluyen la intensidad de dispersión, la sensibilidad del transducer (muchos transductores de fotones comunes son más sensibles a la radiación a 400 nm que a 600 nm) y la intensidad de la fuente.
Preparación de la muestra para su análisis
Aunque la Ecuación\ ref {10.1} y la Ecuación\ ref {10.2} relacionan la dispersión con la concentración de las partículas dispersantes, la intensidad de la radiación dispersa también está influenciada por el tamaño y la forma de las partículas dispersantes. Las muestras que contienen el mismo número de partículas dispersantes pueden mostrar valores significativamente diferentes para —log T o I S dependiendo del diámetro promedio de las partículas. Para un análisis cuantitativo, por lo tanto, es necesario mantener una distribución uniforme de los tamaños de partícula a lo largo de la muestra y entre muestras y estándares.
La mayoría de los métodos turbidimétricos y nefelométricos se basan en la reacción de precipitación para formar las partículas de dispersión. Como aprendimos en el Capítulo 8, las propiedades de un precipitado, incluido el tamaño de partícula, están determinadas por las condiciones en las que se forma. Para mantener una distribución reproducible de tamaños de partícula entre muestras y patrones, es necesario controlar parámetros como la concentración de reactivos, el orden de adición de reactivos, el pH y la temperatura, la velocidad de agitación o agitación, la fuerza iónica y el tiempo entre los precipitados la formación inicial y la medición de transmitancia o dispersión. En muchos casos, se agrega un agente tensoactivo, como glicerol, gelatina o dextrina, para estabilizar el precipitado en estado coloidal y prevenir la coagulación de las partículas.
Aplicaciones
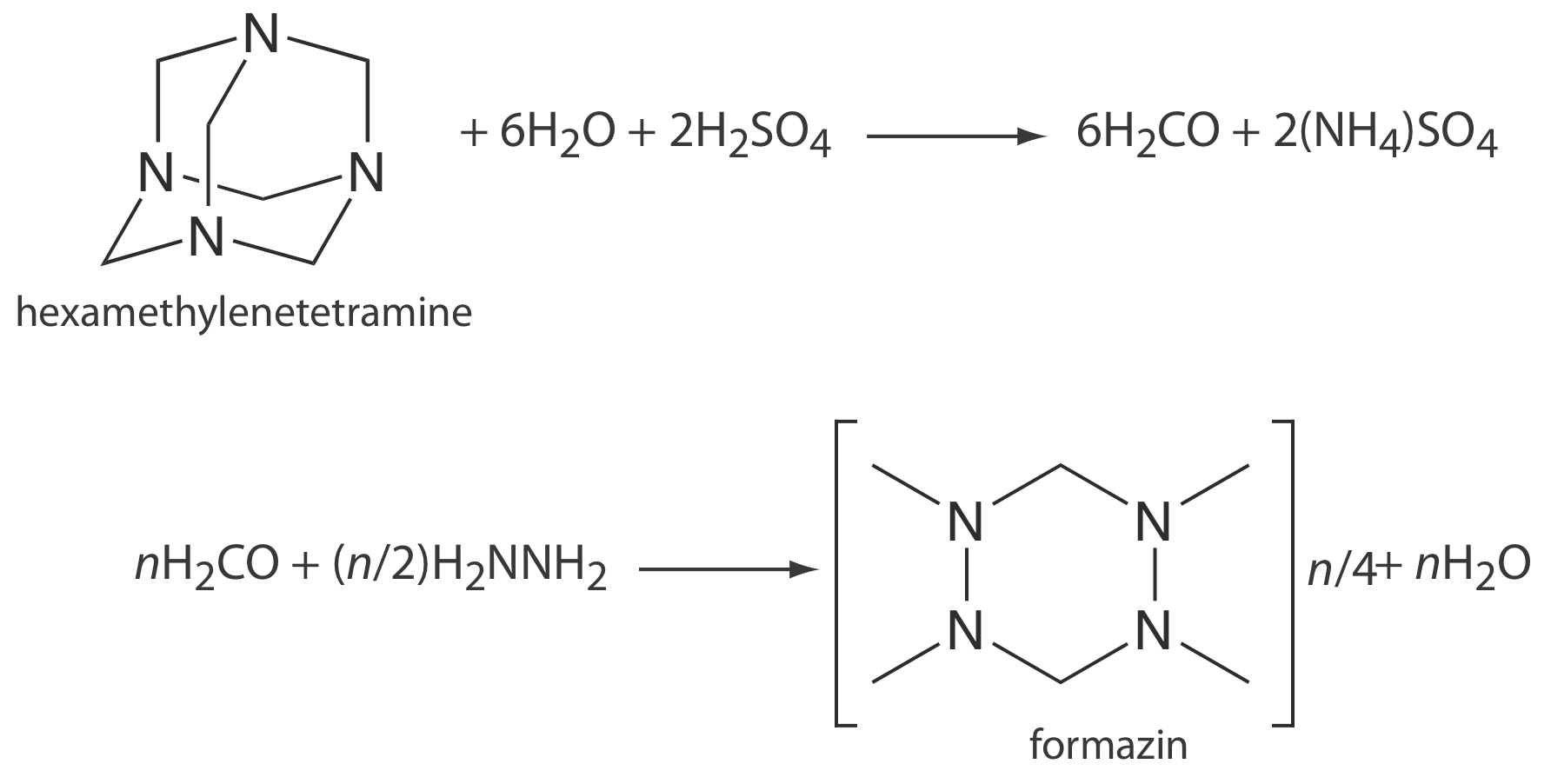
Para determinar la claridad del agua se utilizan turbidimetría y nefelometría. El estándar principal para medir la claridad es la formazina, una suspensión polimérica estable y fácilmente preparada (Figura 10.8.3 ) [Hach, C. C.; Bryant, M. “Turbidity Standards”, Technical Information Series, Folleto No. 12, Hach Company: Loveland, CO, 1995]. Se prepara un patrón madre de formazina combinando una solución de 1g/100 ml de sulfato de hidrazina, N 2 H 4 •H 2 SO 4, con una solución de 10 g/100 mL de hexametilentetramina para producir una suspensión de partículas que se define como 4000 unidades de turbidez nefelométrica (NTU) . Se prepara un conjunto de estándares externos con NTU entre 0 y 40 diluyendo el estándar de stock. Este método se adapta fácilmente al análisis de la claridad del jugo de naranja, cerveza y jarabe de arce.
Se determinan varios cationes y aniones inorgánicos precipitándolos en condiciones bien definidas. La transmitancia o dispersión de la luz, tal como se define por la Ecuación\ ref {10.1} o la Ecuación\ ref {10.2}, es proporcional a la concentración de las partículas dispersantes, la cual, a su vez, está relacionada por la estequiometría de la reacción de precipitación con la concentración del analito. Varios ejemplos de analitos determinados de esta manera se listan en la Tabla 10.8.1 .
Método Representativo 10.8.1: Determinación Turbidimétrica de Sulfato en Agua
La mejor manera de apreciar los detalles teóricos y prácticos discutidos en esta sección es examinar cuidadosamente un método analítico típico. Aunque cada método es único, la siguiente descripción de la determinación de sulfato en agua proporciona un ejemplo instructivo de un procedimiento típico. La descripción aquí se basa en el Método 4500—SO42——C en Métodos Estándar para el Análisis de Agua y Aguas Residuales, Asociación Americana de Salud Pública: Washington, D. C. 20th Ed., 1998.
Descripción del método
Agregar BaCl 2 a una muestra acidificada precipita\(\text{SO}_4^{2-}\) como BaSO 4. La concentración de\(\text{SO}_4^{2-}\) se determina ya sea por turbidimetría o por nefelometría utilizando una fuente incidente de radiación de 420 nm. Se utilizan estándares externos que contienen concentraciones\(\text{SO}_4^{2-}\) conocidas de para estandarizar el método.
Procedimiento
Transferir una muestra de 100 mL a un matraz Erlenmeyer de 250 mL junto con 20.00 mL de un tampón apropiado. Para una muestra que contiene más de 10\(\text{SO}_4^{2-}\) mg/L, la composición del tampón es de 30 g de MgCl 2 •6H 2 O, 5 g de CH 3 Coona•3h 2 O, 1.0 g de KNO 3 y 20 mL de CH 3 COOH glacial por litro. El tampón para una muestra que contiene menos de 10\(\text{SO}_4^{2-}\) mg/L es el mismo excepto por la adición de 0.111 g de Na 2 SO 4 por L.
Colocar la muestra y el tampón en un agitador magnético operado a la misma velocidad para todas las muestras y estándares. Añadir una cucharada de 20—30 malla de BacL 2, usando una cuchara dosificadora con una capacidad de 0.2—0.3 mL, para precipitar el\(\text{SO}_4^{2-}\) como BasO4. Comience el tiempo cuando se agregue el BacL 2 y revuelva la suspensión durante 60 ± 2 s. Cuando la agitación esté completa, deje que la solución se asiente sin agitar durante 5.0± 0.5 min antes de medir su transmitancia o su dispersión.
Prepare una curva de calibración en el rango de 0—40 mg\(\text{SO}_4^{2-}\) /L diluyendo un patrón de stock que sea de 100\(\text{SO}_4^{2-}\) mg/L. Tratar cada patrón usando el procedimiento descrito anteriormente para la muestra. Preparar una curva de calibración y utilizarla para determinar la cantidad de sulfato en la muestra.
Preguntas
1. ¿Cuál es el propósito del búfer?
Si las partículas del precipitado son demasiado pequeñas, I T es demasiado pequeñas para medirlas de manera confiable. Debido a que la precipitación rápida favorece la formación de partículas microcristalinas de BasO 4, utilizamos condiciones que favorecen el crecimiento del precipitado sobre la nucleación de nuevas partículas. La alta fuerza iónica del tampón y su acidez favorecen el crecimiento del precipitado e impiden la formación de BaSO 4 microcristalino.
2. ¿Por qué es importante usar la misma velocidad y tiempo de agitación para las muestras y estándares?
La rapidez y el tiempo que agitamos la muestra después de agregar BaCl 2 influye en el tamaño de las partículas del precipitado.
3. Muchas aguas naturales tienen un ligero color debido a la presencia de ácidos húmicos y fúlvicos, y pueden contener materia suspendida (Figura 10.8.4 ). Explique por qué estos podrían interferir con el análisis de sulfato. Para cada interferente, sugerir una manera de minimizar su efecto en el análisis.

La materia suspendida en una muestra contribuye a la dispersión y, por lo tanto, da como resultado un error determinado positivo. Podemos eliminar esta interferencia filtrando la muestra antes de su análisis. Una muestra coloreada puede absorber parte de la radiación de la fuente, lo que lleva a un error determinado positivo. Podemos compensar esta interferencia tomando una muestra a través del análisis sin agregar BaCl 2. Debido a que no se forma precipitado, utilizamos la transmitancia de esta muestra en blanco para corregir la interferencia.
4. ¿Por qué se agrega Na 2 SO 4 al tampón para muestras que contienen menos de 10 mg\(\text{SO}_4^{2-}\) /L?
La incertidumbre en una curva de calibración es menor cerca de su centro. Si una muestra tiene una alta concentración de\(\text{SO}_4^{2-}\), podemos diluirla para que su concentración caiga cerca de la mitad de la curva de calibración. Para una muestra con una pequeña concentración de\(\text{SO}_4^{2-}\), el tampón aumenta la concentración de sulfato por
\[\begin{array}{c}{\frac{0.111 \ \mathrm{g} \ \mathrm{Na}_{2} \mathrm{SO}_{4}}{\mathrm{L}} \times \frac{96.06 \ \mathrm{g} \ \mathrm{SO}_{4}^{2-}}{142.04 \ \mathrm{g} \ \mathrm{Na}_{2} \mathrm{SO}_{4}} \times} \\ {\qquad \frac{1000 \ \mathrm{mg}}{\mathrm{g}} \times \frac{20.00 \ \mathrm{mL}}{250.0 \ \mathrm{mL}}=6.00 \ \mathrm{mg} \ \mathrm{SO}_{4}^{2-} / \mathrm{L}}\end{array} \nonumber\]
Después de usar la curva de calibración para determinar la cantidad de sulfato en la muestra tal como se analizó, restamos\(\text{SO}_4^{2-}\) 6.00 mg/L para determinar la cantidad de sulfato en la muestra original.
Para evaluar el método descrito en el Método Representativo 10.8.1, se preparó y analizó una serie de estándares externos, proporcionando los resultados que se muestran en la siguiente tabla.
| mg\(\text{SO}_4^{2-}\) /L | transmitancia |
|---|---|
| \ (\ text {SO} _4^ {2-}\) /L">0.00 | 1.00 |
| \ (\ text {SO} _4^ {2-}\) /L">10.00 | 0.646 |
| \ (\ text {SO} _4^ {2-}\) /L">20.00 | 0.417 |
| \ (\ text {SO} _4^ {2-}\) /L">30.00 | 0.269 |
| \ (\ text {SO} _4^ {2-}\) /L">40.00 | 0.174 |
El análisis de una muestra de 100.0-mL de un agua superficial da una transmitancia de 0.538. ¿Cuál es la concentración de sulfato en la muestra?
Solución
La regresión lineal de —log T versus concentración de\(\text{SO}_4^{2-}\) da la curva de calibración que se muestra a continuación, la cual tiene la siguiente ecuación de calibración.
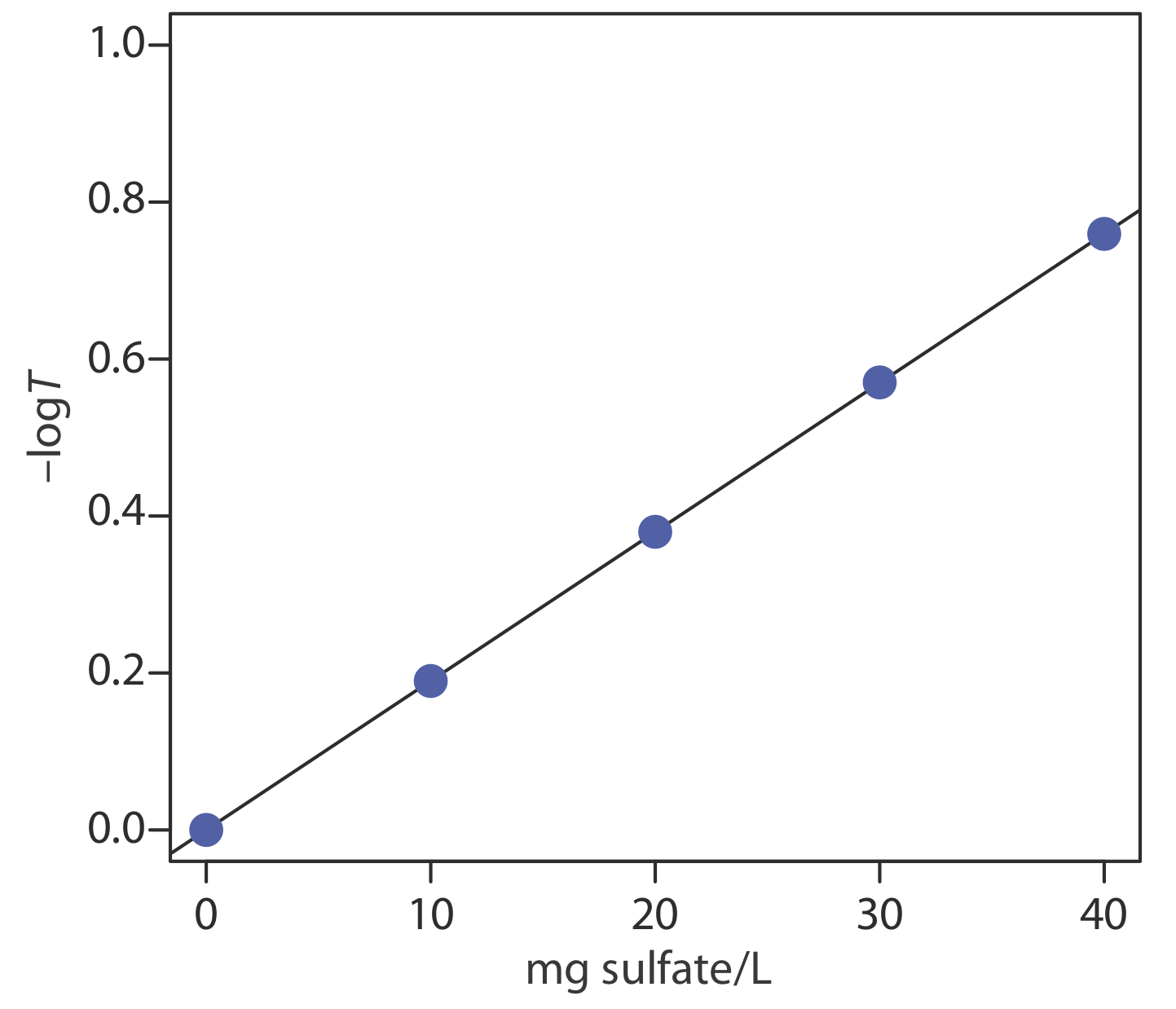
\[-\log T=-1.04 \times 10^{-5}+0.0190 \times \frac{\mathrm{mg} \ \mathrm{SO}_{4}^{2-}}{\mathrm{L}} \nonumber\]
Sustituyendo la transmitancia de la muestra en la ecuación de la curva de calibración da la concentración de sulfato en la muestra como 14.2\(\text{SO}_4^{2-}\) mg/L.


