14.4: Uso de Excel y R para un análisis de varianza

Última actualización
Guardar como PDF

Page ID: 75333

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Aunque los cálculos para un análisis de varianza son relativamente sencillos, se vuelven tediosos cuando se trabaja con grandes conjuntos de datos. Tanto Excel como R incluyen funciones para completar un análisis de varianza. Además, R proporciona una función para identificar la (s) fuente (s) de diferencias significativas dentro del conjunto de datos.

Excel

La herramienta de análisis de Excel incluye una herramienta para ayudarle a completar un análisis de varianza. Vamos a usar el ToolPak para completar un análisis de varianza sobre los datos de la Tabla 14.3.1. Ingrese los datos de la Tabla 14.3.1 en una hoja de cálculo como se muestra en la Figura 14.4.1 .

	A	B	C	D	E
1	replicar	analista A	analista B	analista C	analista D
2	1	94.09	99.55	95.14	93.88
3	2	94.64	98.24	94.62	94.23
4	3	95.08	101.1	95.28	96.05
5	4	94.54	100.4	94.59	93.89
6	5	95.38	100.1	94.24	94.59
7	6	93.62			95.49

Figura 14.4.1 . Porción de una hoja de cálculo que contiene los datos de la Tabla 14.3.1.

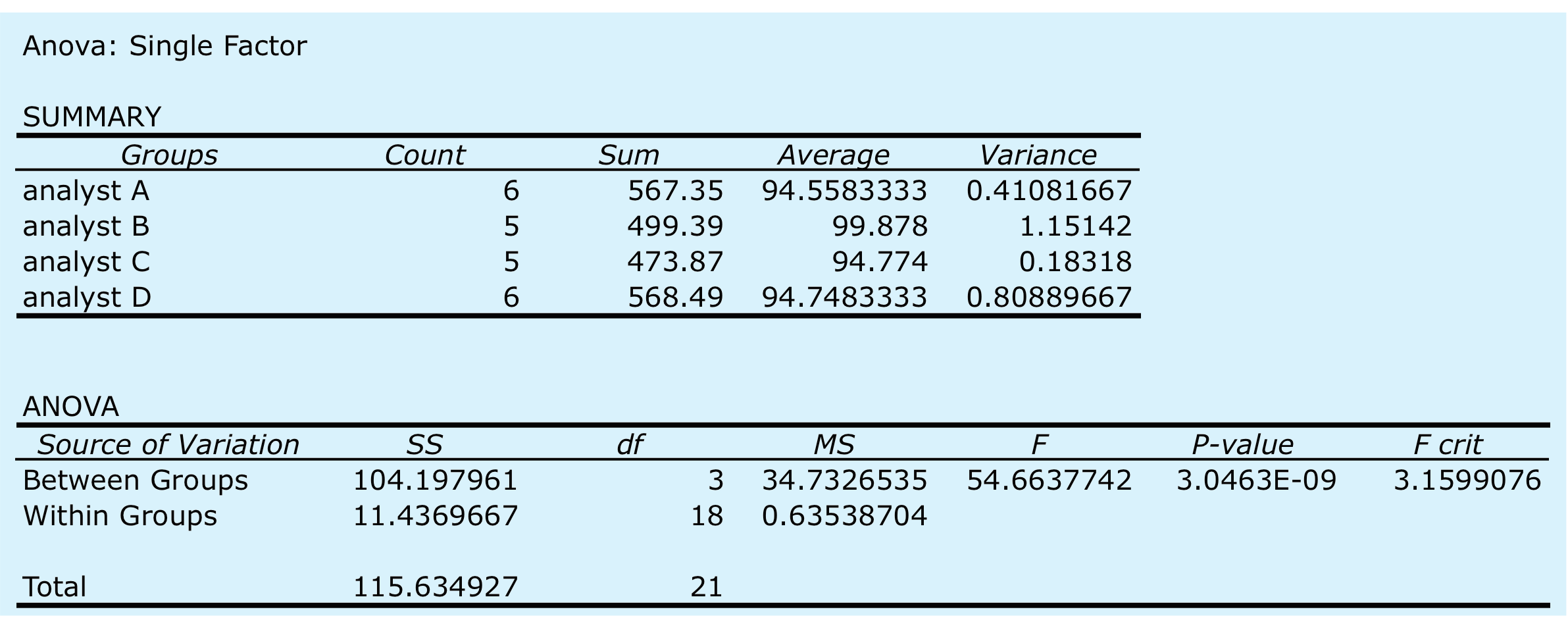
Para completar el análisis de varianza seleccione Análisis de Datos... desde el menú Herramientas, que abre una ventana titulada “Análisis de datos”. Desplácese por la ventana, seleccione Análisis: Factor único de las opciones disponibles y haga clic en Aceptar. Coloque el cursor en el cuadro para el “Rango de entrada” y luego haga clic y arrastre sobre las celdas B1:E7. Selecciona el botón de opción para “Agrupado por: columnas” y marca la casilla de “Etiquetas en la primera fila”. En el cuadro de “Alfa” ingrese 0.05 para\(\alpha\). Seleccione el botón de radio para “Rango de salida”, coloque el cursor en el cuadro y haga clic en una celda vacía; aquí es donde Excel colocará los resultados. Al hacer clic en Aceptar se genera la información que se muestra en la Figura 14.4.2 . El pequeño valor de\(3.05 \times 10^{-9}\) para rechazar falsamente la hipótesis nula indica que existe una fuente significativa de variación entre los analistas.

Figura 14.4.2 . Salida del análisis unidireccional de Excel de varianza de los datos en la Tabla 14.3.1. La tabla de resumen proporciona la media y varianza para cada analista. La tabla ANOVA resume los términos de suma de cuadrados (SS), los grados de libertad (df), las varianzas (MS para el cuadrado medio), el valor de F _exp y el valor crítico de F, y la probabilidad de rechazar incorrectamente el nulo hipótesis de que no hay diferencia significativa entre los analistas.

R

Para completar un análisis de varianza para los datos de la Tabla 14.3.1 usando R, primero necesitamos crear varios objetos. El primer objeto contiene cada resultado de la Tabla 14.3.1.

> resultados = c (94.090, 94.640, 95.008, 94.540, 95.380, 93.620, 99.550, 98.240, 101.100, 100.400, 100.100, 95.140, 94.620, 95.280, 94.590, 94.240, 93.880, 94.230, 96.050, 93.890, 94.950, 95.490)

El segundo objeto contiene etiquetas que identifican el origen de cada entrada en el primer objeto. El siguiente código crea este objeto.

> analista = c (rep (“a” ,6), rep (“b” ,5), rep (“c” ,5), rep (“d” ,6))

A continuación, combinamos los dos objetos en una tabla con dos columnas, una que contiene los datos (resultados) y otra que contiene las etiquetas (analista).

> df= data.frame (resultados, etiquetas= factor (analista))

El factor comando indica que el analista de objetos contiene los factores categóricos para el análisis de varianza. El comando para un análisis de varianza toma la siguiente forma

anova (lm (data ~ factores), data = data.frame)

donde data y factors son las columnas que contienen los datos y los factores categóricos, y data.frame es el nombre que asignamos a la tabla de datos. La figura 14.4.3 muestra la salida resultante. El pequeño valor de\(3.05 \times 10^{-9}\) para rechazar falsamente la hipótesis nula indica que existe una fuente significativa de variación entre los analistas.

Figura 14.4.3 . Salida de una sesión R para un análisis de varianza para los datos del Cuadro 14.3.1. En la tabla, “etiquetas” es la varianza entre muestras y “residuales” es la varianza dentro de la muestra. El valor p de 3.04e-09 es la probabilidad de rechazar incorrectamente la hipótesis nula de que las varianzas dentro de la muestra y entre muestras son las mismas.

Habiendo encontrado una diferencia significativa entre los analistas, queremos identificar la fuente de esta diferencia. R no incluye la prueba de diferencia menos significativa de Fisher, pero sí incluye una función para un método relacionado llamado prueba de diferencia significativa honesta de Tukey. El comando para esta prueba toma la siguiente forma

> TukeyHSD (aov (lm (data ~ factores), data = data.frame), conf. nivel = 0.5)

donde data y factors son las columnas que contienen los datos y los factores categóricos, y data.frame es el nombre que asignamos a la tabla de datos. La figura 14.4.4 muestra la salida de este comando y su interpretación. Los pequeños valores de probabilidad al comparar el analista B con cada uno de los otros analistas indican que esta es la fuente de la diferencia significativa identificada en el análisis de varianza.