14.3: Validar el Método como Método Estándar

Para que un método analítico sea útil, un analista debe ser capaz de lograr resultados de precisión y precisión aceptables. Verificar un método, como se describe en el apartado anterior, establece este objetivo para un solo analista. Otro requisito para un método analítico útil es que un analista obtenga el mismo resultado del día a día, y diferentes laboratorios deben obtener el mismo resultado al analizar la misma muestra. El proceso por el cual aprobamos un método de uso general se conoce como validación e implica una prueba colaborativa del método por parte de analistas en varios laboratorios. Las pruebas colaborativas son utilizadas rutinariamente por agencias reguladoras y organizaciones profesionales, como la Agencia de Protección Ambiental de los Estados Unidos, la Sociedad Americana de Pruebas y Materiales, la Asociación de Químicos Analíticos Oficiales y la Asociación Americana de Salud Pública. Muchos de los métodos representativos de capítulos anteriores son identificados por estas agencias como métodos validados.

Cuando un analista realiza un análisis único en una sola muestra, la diferencia entre el valor determinado experimentalmente y el valor esperado está influenciada por tres fuentes de error: errores aleatorios, errores sistemáticos inherentes al método y errores sistemáticos exclusivos del analista. Si el analista realiza suficientes análisis replicados, entonces podemos trazar una distribución de resultados, como se muestra en la Figura {{template.Index (ID:1)} a. El ancho de esta distribución se describe mediante una desviación estándar que proporciona una estimación de los errores aleatorios que afectan al análisis. La posición de la media de la distribución\(\overline{X}\), relativa al valor real de la muestra\(\mu\), está determinada tanto por errores sistemáticos inherentes al método como por aquellos errores sistemáticos únicos del analista. Para un solo analista no hay forma de separar el error sistemático total en sus partes componentes.

Figura 14.3.1 . Particionamiento de errores aleatorios, errores sistemáticos debidos al analista y errores sistemáticos debidos al método para (a) análisis replicados realizados por un solo analista y (b) determinaciones únicas realizadas por varios analistas.

El objetivo de una prueba colaborativa es determinar la magnitud de las tres fuentes de error. Si varios analistas analizan cada uno la misma muestra una vez, la variación en sus resultados colectivos (ver Figura 14.3.1 b) incluye contribuciones de errores aleatorios y errores sistemáticos (sesgos) únicos para los analistas. Sin información adicional, no podemos separar la desviación estándar de estos datos agrupados en la precisión del análisis y los errores sistemáticos introducidos por los analistas. Podemos utilizar la posición de la distribución, para detectar la presencia de un error sistemático en el método.

Pruebas colaborativas de dos muestras

El diseño de una prueba colaborativa debe proporcionar la información adicional necesaria para separar los errores aleatorios de los errores sistemáticos introducidos por los analistas. Un enfoque sencillo —aceptado por la Asociación de Químicos Analíticos Oficiales— es que cada analista analice dos muestras que sean similares tanto en su matriz como en su concentración de analito. Para analizar los resultados representamos a cada analista como un punto único en una gráfica de dispersión de dos muestras, utilizando el resultado para una muestra como la coordenada x y el resultado para la otra muestra como la coordenada y [Youden, W. J. “Statistical Techniques for Collaborative Tests”, en Manual Estadístico de la Asociación de Químicos Analíticos Oficiales, Asociación de Químicos Analíticos Oficiales: Washington, D. C., 1975, pp 10—11].

Como se muestra en la Figura 14.3.2 , un gráfico de dos muestras coloca a cada analista en uno de los cuatro cuadrantes, los cuales identificamos como (+, +), (—, +), (—, —) y (+, —). Un signo más indica que el resultado del analista para una muestra es mayor que la media para todos los analistas y un signo menos indica que el resultado del analista es menor que la media para todos los analistas. El cuadrante (+, —), por ejemplo, contiene aquellos analistas que superaron la media para la muestra X y que subestimaron la media para la muestra Y. Si la variación en los resultados está dominada por errores aleatorios, entonces esperamos que los puntos se distribuyan aleatoriamente en los cuatro cuadrantes, con un número igual de puntos en cada cuadrante. Además, como se muestra en la Figura 14.3.2 a, los puntos se agruparán en un patrón circular cuyo centro son los valores medios para las dos muestras. Cuando los errores sistemáticos son significativamente mayores que los errores aleatorios, entonces los puntos caen principalmente en los cuadrantes (+, +) y (—, —), formando un patrón elíptico alrededor de una línea que biseca estos cuadrantes en un ángulo de 45 ^o, como se ve en la Figura 14.3.2 b.

Figura 14.3.2 . Gráficas típicas de dos muestras cuando (a) los errores aleatorios son significativamente mayores que los errores sistemáticos debidos a los analistas, y (b) cuando los errores sistemáticos debidos a los analistas son significativamente mayores que los errores aleatorios.

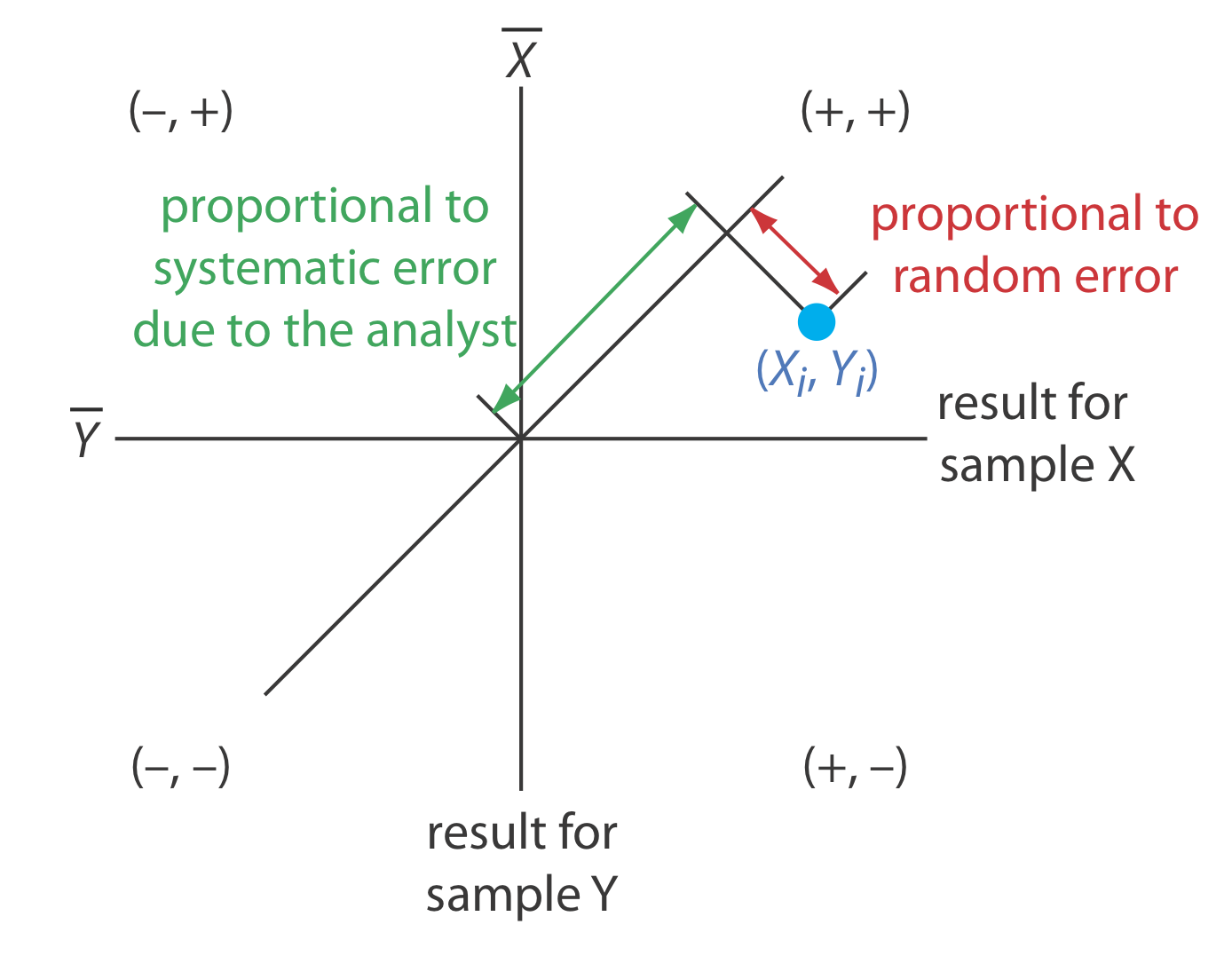
Una inspección visual de un gráfico de dos muestras es un método efectivo para evaluar cualitativamente las capacidades de un método estándar propuesto, como se muestra en la Figura 14.3.3 . La longitud de una línea perpendicular desde cualquier punto a la línea de 45 ^o es proporcional al efecto del error aleatorio en los resultados de ese analista. La distancia desde la intersección de los ejes —que corresponde a los valores medios de las muestras X e Y — hasta la proyección perpendicular de un punto en la línea de 45 ^o es proporcional al error sistemático del analista. Un método estándar ideal tiene pequeños errores aleatorios y pequeños errores sistemáticos debido a los analistas, y tiene una agrupación compacta de puntos que es más circular que elíptica.

Figura 14.3.3 . Relación entre el resultado para un solo analista (en azul) y la contribución del error aleatorio (flecha roja) y la contribución del error sistemático del analista (flecha verde).

También podemos usar los datos en un gráfico de dos muestras para separar la variación total de los datos, en contribuciones de error aleatorio\(\sigma_\text{tot}\), y de errores sistemáticos debidos a los analistas\(\sigma_\text{rand}\),\(\sigma_\text{syst}\) [Youden, W. J. “Statistical Techniques for Collaborative Tests”, en Statistical Manual de la Asociación de Químicos Analíticos Oficiales, Asociación de Químicos Analíticos Oficiales: Washington, D. C., 1975, pp 22—24]. Debido a que los errores sistemáticos de un analista están presentes en su análisis de ambas muestras, la diferencia, D, entre los resultados estima la contribución del error aleatorio.

\[D = X_i - Y_i \nonumber\]

Para estimar la contribución total a partir del error aleatorio utilizamos la desviación estándar de estas diferencias, s _D, para todos los analistas

\[s_D = \sqrt{\frac {\sum_{i = 1}^n (D_i - \overline{D})^2} {2(n-1)}} = s_\text{rand} \approx \sigma_\text{rand} \label{14.1}\]

donde n es el número de analistas. El factor de 2 en el denominador de la Ecuación\ ref {14.1} es el resultado de usar dos valores para determinar D _i. El total, T, de los resultados de cada analista

\[T_i = X_i + Y_i \nonumber\]

contiene contribuciones tanto del error aleatorio como del doble del error sistemático del analista.

\[\sigma_{\mathrm{tot}}^{2}=\sigma_{\mathrm{rand}}^{2}+2 \sigma_{\mathrm{syst}}^{2} \label{14.2}\]

La desviación estándar de los totales, s _T, proporciona una estimación para\(\sigma_\text{tot}\).

\[s_{T}=\sqrt{\frac{\sum_{i=1}^{n}\left(T_{i}-\overline{T}\right)^{2}}{2(n-1)}}=s_{tot} \approx \sigma_{tot} \label{14.3}\]

Nuevamente, el factor de 2 en el denominador es el resultado de utilizar dos valores para determinar T _i.

Si los errores sistemáticos son significativamente mayores que los errores aleatorios, entonces s _T es mayor que s _D, hipótesis que podemos evaluar usando una prueba F de una cola

\[F=\frac{s_{T}^{2}}{s_{D}^{2}} \nonumber\]

donde los grados de libertad tanto para el numerador como para el denominador son n — 1. Como se muestra en el siguiente ejemplo, si s _T es significativamente mayor que s _D podemos usar la Ecuación\ ref {14.2} para separar\(\sigma_\text{tot}^2\) en componentes que representan el error aleatorio y el error sistemático.

Ejemplo 14.3.1

Como parte de un estudio colaborativo de un nuevo método para determinar la cantidad de colesterol total en sangre, se envían dos muestras a 10 analistas con instrucciones que analizan cada muestra una vez. Se le devuelven los siguientes resultados, en mg de colesterol total por cada 100 mL de suero.

analista	muestra 1	muestra 2
1	245.0	229.4
2	247.4	249.7
3	246.0	240.4
4	244.9	235.5
5	255.7	261.7
6	248.0	239.4
7	249.2	255.5
8	255.1	224.3
9	255.0	246.3
10	243.1	253.1

Utilice esta estimación de datos\(\sigma_\text{rand}\) y\(\sigma_\text{syst}\) para el método.

Solución

La Figura 14.3.4 proporciona una gráfica de dos muestras de los resultados. La agrupación de puntos sugiere que los errores sistemáticos de los analistas son significativos. La línea vertical a 245.9 mg/100 mL es el valor promedio para la muestra 1 y el valor promedio para la muestra 2 se indica por la línea horizontal en 243.5 mg/100 mL. Estimar\(\sigma_\text{rand}\) y primero\(\sigma_\text{syst}\) calculamos los valores para D _i y T _i.

analista	D i	T i
1	15.6	474.4
2	—2.3	497.1
3	5.6	486.4
4	9.4	480.4
5	—6.0	517.4
6	8.6	487.4
7	—6.3	504.7
8	0.8	449.4
9	8.7	501.3
10	—10.0	496.2

A continuación, calculamos las desviaciones estándar para las diferencias, s _D, y los totales, s _T, usando la Ecuación\ ref {14.1} y la Ecuación\ ref {14.2}, obteniendo s _D = 5.95 y s _T = 13.3. Para determinar si los errores sistemáticos entre los analistas son significativos, utilizamos una prueba F para comparar s _T y s _D.

\[F=\frac{s_{T}^{2}}{s_{D}^{2}}=\frac{(13.3)^{2}}{(5.95)^{2}}=5.00 \nonumber\]

Debido a que la relación F es mayor que F (0.05,9,9), que es 3.179, concluimos que los errores sistemáticos entre los analistas son significativos en el nivel de confianza del 95%. La precisión estimada para un solo analista es

\[\sigma_{\mathrm{rand}} \approx s_{\mathrm{rand}}=s_{D}=5.95 \nonumber\]

La desviación estándar estimada por errores sistemáticos entre analistas se calcula a partir de la Ecuación\ ref {14.2}.

\[\sigma_\text{syst} = \sqrt{\frac {\sigma_\text{tot}^2 - \sigma_\text{rand}^2} {2}} \approx \sqrt{\frac {s_t^2 - s_D^2} {2}} = \sqrt{\frac {(13.3)^2-(5.95)^2} {2}} = 8.41 \nonumber\]

Figura 14.3.4 . Gráfica de dos muestras para los datos del Ejemplo 14.3.1 . El número por cada punto azul indica al analista. Los valores verdaderos para cada muestra (ver Ejemplo 14.3.2 ) están indicados por la estrella roja.

Si se conocen los valores verdaderos para las dos muestras, también podemos probar la presencia de un error sistemático en el método. Si no hay errores sistemáticos del método, entonces la suma de los valores verdaderos,\(\mu_\text{tot}\), para las muestras X e Y

\[\mu_{\mathrm{tot}}=\mu_{X}+\mu_{Y} \nonumber\]

debe caer dentro del intervalo de confianza alrededor de T. Podemos usar una prueba t de dos colas de las siguientes hipótesis nulas y alternativas

\[H_{0} : \overline{T}=\mu_{\mathrm{tot}} \quad H_{\mathrm{A}} : \overline{T} \neq \mu_{\mathrm{tot}} \nonumber\]

para determinar si existe evidencia de un error sistemático en el método. El estadístico de prueba, t _exp, es

\[t_\text{exp} = \frac {|\overline{T} - \mu_\text{tot}|\sqrt{n}} {s_T\sqrt{2}} \label{14.4}\]

con n — 1 grados de libertad. Incluimos el 2 en el denominador porque s _T (ver Ecuación\ ref {14.3} subestima la desviación estándar\(\overline{T}\) al comparar con\(\mu_\text{tot}\).

Ejemplo 14.3.2

Se sabe que las dos muestras analizadas en el Ejemplo 14.3.1 contienen las siguientes concentraciones de colesterol:\(\mu_\text{samp 1}\) = 248.3 mg/100 mL y\(\mu_\text{samp 2}\) = 247.6 mg/100 mL. Determinar si existe alguna evidencia de error sistemático en el método al nivel de confianza del 95%.

Solución

Usando los datos del Ejemplo 14.3.1 y los valores verdaderos para las muestras, sabemos que s _T es 13.3, y que

\[\overline{T} = \overline{X}_\text{samp 1 } + \overline{X}_\text{samp 2 } = 245.9 + 243.5 = 489.4 \text{ mg/100 mL} \nonumber\]

\[\mu_\text{tot} = \mu_\text{samp 1 } + mu_\text{samp 2 } = 248.3 + 247.6 = 495.9 \text{ mg/100 mL} \nonumber\]

Sustituyendo estos valores en la Ecuación\ ref {14.4} da

\[t_{\mathrm{exp}}=\frac{|489.4-495.9| \sqrt{10}}{13.3 \sqrt{2}}=1.09 \nonumber\]

Debido a que este valor para t _exp es menor que el valor crítico de 2.26 para t (0.05, 9), no hay evidencia de un error sistemático en el método al nivel de confianza del 95%.

Ejemplo 14.3.1 y Ejemplo 14.3.2 ilustran cómo podemos usar un par de muestras similares en una prueba colaborativa de un nuevo método. Idealmente, una prueba colaborativa involucra varios pares de muestras que abarcan el rango de concentraciones de analito para las que planeamos usar el método. Al hacerlo, evaluamos el método para fuentes constantes de error y establecemos la desviación estándar relativa esperada y el sesgo para diferentes niveles de analito.

Pruebas colaborativas y análisis de varianza

En una prueba colaborativa de dos muestras pedimos a cada analista que realice una sola determinación en cada una de las dos muestras separadas. Después de reducir los datos a un conjunto de diferencias, D, y un conjunto de totales, T, cada uno caracterizado por una media y una desviación estándar, extraemos valores para los errores aleatorios que afectan la precisión y las diferencias sistemáticas entre entonces analistas. Los cálculos son relativamente simples y directos.

Un enfoque alternativo a una prueba colaborativa es hacer que cada analista realice varias determinaciones replicadas en una sola muestra común. Este enfoque genera un conjunto de datos separado para cada analista y requiere un tratamiento estadístico diferente para proporcionar estimaciones para\(\sigma_\text{rand}\) y para\(\sigma_\text{syst}\).

Existen varios métodos estadísticos para comparar tres o más conjuntos de datos. El enfoque que consideramos en esta sección es un análisis de varianza (ANOVA). En su forma más simple, un ANOVA unidireccional nos permite explorar la importancia de una sola variable —la identidad del analista es un ejemplo— sobre la varianza total. Para evaluar la importancia de esta variable, comparamos su varianza con la varianza explicada por fuentes indeterminadas de error.

Primero introdujimos la varianza en el Capítulo 4 como una medida de la dispersión de un conjunto de datos alrededor de su tendencia central. En el contexto de un análisis de varianza, es útil para nosotros entender que la varianza es simplemente una relación de dos términos: una suma de cuadrados para las diferencias entre los valores individuales y su media, y los grados de libertad. Por ejemplo, la varianza, s ², de un conjunto de datos que consiste en n mediciones es

\[s^{2}=\frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}{n-1} \nonumber\]

donde X _i es el valor de una sola medida y\(\overline{X}\) es la media. La capacidad de dividir la varianza en una suma de cuadrados y los grados de libertad simplifica enormemente los cálculos en un ANOVA unidireccional.

Vamos a usar un ejemplo simple para desarrollar la justificación detrás de un cálculo ANOVA unidireccional. Los datos de la Tabla 14.3.1 son de cuatro analistas, a cada uno de los cuales se les pidió determinar la pureza de una sola preparación farmacéutica de sulfanilamida. Cada columna de la Tabla 14.3.1 proporciona los resultados para un analista individual. Para ayudarnos a realizar un seguimiento de estos datos, representaremos cada resultado como X _ij, donde i identifica al analista y j indica la réplica. Por ejemplo, X _3,5 es la quinta réplica para el tercer analista, o 94.24%.

Tabla 14.3.1 . Determinación del% de pureza de una preparación de sulfanilamida por cuatro analistas

replicar	analista A	analista B	analista C	analista D
1	94.09	99.55	95.14	93.88
2	94.64	98.24	94.62	94.23
3	95.08	101.1	95.28	96.05
4	94.54	100.4	94.59	93.89
5	95.38	100.1	94.24	94.95
6	93.62	—	—	95.49
\(\overline{X}\)	94.56	99.88	94.77	94.75
s	0.641	1.073	0.428	0.899

Los datos de la Tabla 14.3.1 muestran variabilidad en los resultados obtenidos por cada analista y en la diferencia en los resultados entre los analistas. Existen dos fuentes para esta variabilidad: los errores indeterminados asociados al procedimiento analítico que cada analista experimenta por igual, y los errores sistemáticos o determinados introducidos por los analistas individuales.

Una forma de ver los datos en la Tabla 14.3.1 es tratarlos como una sola muestra grande, caracterizada por una media global y una varianza global

\[\overline{\overline{X}}=\frac{\sum_{i=1}^{h} \sum_{i=1}^{n} X_{ij}}{N} \label{14.5}\]

\[\overline{\overline{s^{2}}}=\frac{\sum_{i=1}^{h} \sum_{j=1}^{n_{i}}\left(X_{i j}-\overline{\overline{X}}\right)^{2}}{N-1} \label{14.6}\]

donde h es el número de muestras (en este caso el número de analistas), n _i es el número de réplicas para la i-ésima muestra (en este caso el i-ésimo analista), y N es el número total de puntos de datos (en este caso 22). La variación global, que incluye todas las fuentes de variabilidad que afectan a los datos, proporciona una estimación de la influencia combinada de errores indeterminados y errores sistemáticos.

Una segunda forma de trabajar con los datos de la Tabla 14.3.1 es tratar los resultados de cada analista por separado. Si asumimos que cada analista experimenta los mismos errores indeterminados, entonces la varianza, s ², para cada analista proporciona una estimación separada de\(\sigma_\text{rand}^2\). Para agrupar estas varianzas individuales, que llamamos varianza dentro de la muestra\(s_w^2\), cuadramos la diferencia entre cada réplica y su media correspondiente, las sumamos y dividimos por los grados de libertad.

\[\sigma_{\mathrm{rnd}}^{2} \approx s_{w}^{2}=\frac{\sum_{i=1}^{h} \sum_{j=1}^{n_{i}}\left(X_{i j}-\overline{X}_{i}\right)^{2}}{N-h} \label{14.7}\]

Compare cuidadosamente nuestra descripción de la Ecuación\ ref {14.7} con la ecuación misma. Es importante que entiendas por qué la ecuación\ ref {14.7} proporciona nuestra mejor estimación de los errores indeterminados que afectan a los datos en la Tabla 14.3.1 . Tenga en cuenta que perdemos un grado de libertad por cada una de las h medias incluidas en el cálculo.

Para estimar los errores sistemáticos\(\sigma_\text{syst}^2\),, que afectan los resultados en la Tabla 14.3.1 necesitamos considerar las diferencias entre los analistas. La varianza de los valores medios individuales sobre la media global, a la que llamamos varianza entre muestras,\(s_b^2\), es

\[s_{b}^{2}=\frac{\sum_{i=1}^{h} n_{i}\left(\overline{X}_{i}-\overline{\overline{X}}\right)^{2}}{h-1} \label{14.8}\]

donde perdemos un grado de libertad para la media global. La varianza entre muestras incluye contribuciones tanto de errores indeterminados como de errores sistemáticos; así

\[s_b^2 = \sigma_\text{rand}^2 + \overline{n}\sigma_\text{syst}^2 \label{14.9}\]

donde\(\overline{n}\) es el promedio de réplicas por analista.

\[\overline{n}=\frac{\sum_{i=1}^{h} n_{i}}{h} \nonumber\]

Observe la similitud entre la Ecuación\ ref {14.9} y la Ecuación\ ref {14.2}. El análisis de los datos en una gráfica de dos muestras es lo mismo que un análisis de varianza unidireccional con h = 2.

En un ANOVA unidireccional de los datos de la Tabla 14.3.1 hacemos la hipótesis nula de que no hay diferencias significativas entre los valores medios para los analistas. La hipótesis alternativa es que al menos uno de los valores medios es significativamente diferente. Si la hipótesis nula es verdadera, entonces\(\sigma_\text{syst}^2\) debe ser cero y\(s_w^2\) y\(s_b^2\) debe tener valores similares. Si\(s_b^2\) es significativamente mayor que\(s_w^2\), entonces\(\sigma_\text{syst}^2\) es mayor que cero. En este caso debemos aceptar la hipótesis alternativa de que existe una diferencia significativa entre los medios para los analistas. El estadístico de prueba es la relación F

\[F_{\mathrm{exp}}=\frac{s_{b}^{2}}{s_{w}^{2}} \nonumber\]

que se compara con el valor crítico F (a, h — 1, N — h). Se trata de una prueba de significancia de una cola porque sólo nos interesa si\(s_b^2\) es significativamente mayor que\(s_w^2\).

Ambos\(s_b^2\) y\(s_w^2\) son fáciles de calcular para conjuntos de datos pequeños. Para conjuntos de datos más grandes, calcular\(s_w^2\) es tedioso. Podemos simplificar los cálculos aprovechando la relación entre los términos de suma de cuadrados para la varianza global (Ecuación\ ref {14.6}), la varianza dentro de la muestra (ecuación ref {14.7}) y la varianza entre muestras (Ecuación\ ref {14.8}). Podemos dividir el numerador de la Ecuación\ ref {14.6}, que es la suma total de cuadrados, SS _t, en dos términos

\[SS_t = SS_w + SS_b \nonumber\]

donde SS _w es la suma de cuadrados para la varianza dentro de la muestra y SS _b es la suma de cuadrados para la varianza entre muestras. El cálculo de SS _t y SS _b da SS _w por diferencia. Finalmente, dividir SS _w y SS _b por sus respectivos grados de libertad da\(s_w^2\) y\(s_b^2\). La Tabla 14.3.2 resume las ecuaciones para un cálculo ANOVA unidireccional. El ejemplo 14.3.3 te guía a través de los cálculos, usando los datos de la Tabla 14.3.1 .

Tabla 14.3.2 . Resumen de cálculos para un análisis de varianza unidireccional

fuente	suma de cuadrados	grados de libertad	varianza	varianza esperada	Relación F
entre muestras	\(SS_b = \sum_{i = 1}^h n_i (\overline{X}_i - \overline{\overline{X}})^2\)	\(h - 1\)	\(s_b^2 = \frac {SS_b} {h - 1}\)	\(s_b^2 = \sigma_\text{rand}^2 + \overline{n}\sigma_\text{syst}^2\)	\(F_\text{exp} = \frac {s_b^2} {s_w^2}\)
dentro de muestras	\(SS_t = SS_w + SS_b\)	\(N - h\)	\(s_w^2 = \frac {SS_w} {N - h}\)	\(s_w^2 = \sigma_\text{rand}^2\)
total	\(SS_t = \sum_{i = 1}^h \sum_{j = 1}^{n_i}(X_{ij} - \overline{\overline{X}})^2\) \(SS_t = \overline{\overline{s^2}}(N - 1)\)	\(N - 1\)

Ejemplo 14.3.3

Los datos de la Tabla 14.3.1 son de cuatro analistas, a cada uno de los cuales se les pidió determinar la pureza de una sola preparación farmacéutica de sulfanilamida. Determinar si la diferencia en sus resultados es significativa en\(\alpha = 0.05\). Si existe tal diferencia, estime los valores para\(\sigma_\text{rand}^2\) y\(\sigma_\text{syst}\).

Solución

Para comenzar calculamos la media global (Ecuación\ ref {14.5}) y la varianza global (Ecuación\ ref {14.6}) para los datos agrupados, y las medias para cada analista; estos valores se resumen aquí.

\[\overline{\overline{X}} = 95.87 \quad \quad \overline{\overline{s^2}} = 5.506 \nonumber\]

\[\overline{X}_A = 94.56 \quad \overline{X}_B = 99.88 \quad \overline{X}_C = 94.77 \quad \overline{X}_D = 94.75 \nonumber\]

Usando estos valores calculamos la suma total de cuadrados

\[S S_{t}=\overline{\overline{s^{2}}}(N-1)=(5.506)(22-1)=115.63 \nonumber\]

la suma de cuadrados entre muestras

\[S S_{b}=\sum_{i=1}^{h} n_{i}\left(\overline{X}_{i}-\overline{\overline{X}}\right)^{2}=6(94.56-95.87)^{2}+5(99.88-95.87)^{2}+5(94.77-95.87)^{2}+6(94.75-95.87)^{2}=104.27 \nonumber\]

y la suma de cuadrados dentro de la muestra

\[S S_{w}=S S_{t}-S S_{b}=115.63-104.27=11.36 \nonumber\]

El resto de los cálculos necesarios se resumen en la siguiente tabla.

fuente	suma de cuadrados	grados de libertad	varianza
entre muestras	104.27	\(h - 1 = 4 - 1 = 3\)	34.76
dentro de muestras	11.36	\(N - h = 22 - 4 = 18\)	0.631

Comparando las varianzas encontramos que

\[F_{\mathrm{exp}}=\frac{s_{b}^{2}}{s_{w}^{2}}=\frac{34.76}{0.631}=55.09 \nonumber\]

Debido a que F _exp es mayor que F (0.05, 3, 18), que es 3.16, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que el trabajo de al menos un analista es significativamente diferente del resto de analistas. Nuestra mejor estimación de la varianza dentro de la muestra es

\[\sigma_{\text {rand}}^{2} \approx s_{w}^{2}=0.631 \nonumber\]

y nuestra mejor estimación de la varianza entre muestras es

\[\sigma_\text{syst}^2 = \frac {s_b^2 - s_w^2} {\overline{n}} = \frac {35.76 - 0.631} {22/4} = 6.205 \nonumber\]

En este ejemplo la varianza debida a diferencias sistemáticas entre los analistas es casi un orden de magnitud mayor que la varianza debida a la precisión del método.

Habiendo demostrado que existe una diferencia significativa entre los analistas, podemos usar una versión modificada de la prueba t, conocida como la diferencia menos significativa de Fisher, para determinar la fuente de la diferencia. El estadístico de prueba para comparar dos valores medios es la prueba t del Capítulo 4, excepto que reemplazamos la desviación estándar agrupada, s _pool, por la raíz cuadrada de la varianza dentro de la muestra del análisis de varianza.

\[t_{\mathrm{exp}}=\frac{\left|\overline{X}_{1}-\overline{X}_{2}\right|}{\sqrt{s_{w}^{2}}} \times \sqrt{\frac{n_{1} n_{2}}{n_{1}+n_{2}}} \label{14.10}\]

Comparamos t _exp con su valor crítico\(t(\alpha, \nu)\) utilizando el mismo nivel de significancia que el cálculo del ANOVA. Los grados de libertad son los mismos que para la varianza dentro de la muestra. Dado que nos interesa saber si la mayor de las dos medias es significativamente mayor que la otra media, el valor de\(t(\alpha, \nu)\) es el de una prueba de significancia de una cola.

Podría preguntarse por qué nos molestamos con el análisis de varianza si estamos planeando usar una prueba t para comparar pares de analistas. Cada t -test lleva una probabilidad,\(\alpha\), de afirmar que una diferencia es significativa aunque no lo sea (un error tipo 1). Si\(\alpha\) establecemos en 0.05 y completamos seis pruebas t, la probabilidad de un error tipo 1 aumenta a 0.265. Saber que hay una diferencia significativa dentro de un conjunto de datos, lo que obtenemos del análisis de la varianza, protege la prueba t.

Ejemplo 14.3.4

En Ejemplo 14.3.3 mostramos que existe una diferencia significativa entre el trabajo de los cuatro analistas en la Tabla 14.3.1 . Determinar la fuente de esta diferencia significativa.

Solución

Las comparaciones individuales mediante la prueba de diferencia menos significativa de Fisher se basan en la siguiente hipótesis nula y la hipótesis alternativa de una cola apropiada.

\[H_0: \overline{X}_1 = \overline{X}_2 \quad \quad H_A: \overline{X}_1 > \overline{X}_2 \quad \text{or} \quad H_A: \overline{X}_1 < \overline{X}_2 \nonumber\]

Usando la ecuación\ ref {14.10} calculamos valores de t _exp para cada posible comparación y los comparamos con el valor crítico de una cola de 1.73 para t (0.05, 18). Por ejemplo, t _exp para los analistas A y B es

\[\left(t_{exp}\right)_{AB}=\frac{|94.56-99.88|}{\sqrt{0.631}} \times \sqrt{\frac{6 \times 5}{6+5}}=11.06 \nonumber\]

Debido a que (t _exp) _AB es mayor que t (0.05,18) rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que los resultados para el analista B son significativamente mayores que los del analista A. Continuando con los otros pares es fácil demostrar que (t _exp) _AC es 0.437, (t _exp) _AD es 0.414, (t _exp) _BC es 10.17, (t exp _exp) _BD es 10.67, y (t _exp) _CD es 0.04.. Colectivamente, estos resultados sugieren que existe una diferencia sistemática significativa entre el trabajo del analista B y el trabajo de los demás analistas. Por supuesto, no hay forma de decidir si alguno de los cuatro analistas ha realizado un trabajo acertado.

Tenemos evidencia de que el resultado del analista B es significativamente diferente de los resultados de los analistas A, C y D, y no tenemos evidencia de que haya alguna diferencia significativa entre los resultados de los analistas A, C y D . No sabemos si los resultados del analista B son precisos, o si los resultados de los analistas A, C y D son precisos. De hecho, es posible que ninguno de los resultados de la Tabla 14.3.1 sea exacto.

Podemos extender un análisis de varianza a sistemas que involucren más de una sola variable. Por ejemplo, podemos usar un ANOVA bidireccional para determinar el efecto sobre un método analítico tanto del analista como de la instrumentación. El tratamiento del ANOVA multivariado está fuera del alcance de este texto, pero está cubierto en varios de los textos enumerados en los recursos adicionales de este capítulo.

¿Qué es un resultado razonable para un estudio colaborativo?

Las pruebas colaborativas nos proporcionan un método para estimar la variabilidad (o reproducibilidad) entre analistas en diferentes laboratorios. Si la variabilidad es significativa, podemos determinar qué porción se debe a errores de método indeterminados,\(\sigma_\text{rand}^2\), y qué porción se debe a diferencias sistemáticas entre los analistas,\(\sigma_\text{syst}^2\). Lo que queda sin respuesta es la siguiente pregunta importante: ¿Cuál es un valor razonable para la reproducibilidad de un método?

Un análisis de casi 10 000 estudios colaborativos sugiere que una estimación razonable para la reproducibilidad de un método es

\[R=2^{(1-0.5 \log C)} \label{14.11}\]

donde R es el porcentaje de desviación estándar relativa para los resultados incluidos en el estudio colaborativo y C es la cantidad fraccionaria de analito en la muestra sobre una base peso a peso. Se cree que la ecuación\ ref {14.1} es independiente del tipo de analito, el tipo de matriz y el método de análisis. Por ejemplo, cuando una muestra en un estudio colaborativo contiene 1 microgramo de analito por gramo de muestra, C es 10 ^—6 la desviación estándar relativa estimada es

\[R=2^{\left(1-0.5 \log 10^{-6}\right)}=16 \% \nonumber\]

Ejemplo 14.3.5

¿Cuál es la desviación estándar relativa estimada para los resultados de un estudio colaborativo cuando la muestra es analito puro (100% w/w analito)? Repita para el caso donde la concentración del analito sea 0.1% w/w.

Solución

Cuando la muestra es 100% p/p de analito (C = 1) la desviación estándar relativa estimada es

\[R=2^{(1-0.5 \log 1)}=2 \% \nonumber\]

Esperamos que aproximadamente dos tercios de los participantes en el estudio colaborativo (\(\pm 1 \sigma\)) reportarán la concentración del analito dentro del rango de 98% w/w a 102% w/w. Si la concentración del analito es 0.1% w/w (C = 0.001), la desviación estándar relativa estimada es

\[R=2^{(1-0.5 \log 0.01)}=5.7 \% \nonumber\]

y esperamos que aproximadamente dos tercios de los analistas reportarán la concentración del analito dentro del rango de 0.094% w/w a 0.106% w/w.

Por supuesto, la Ecuación\ ref {14.11} solo estima el estándar relativo esperado. Si la desviación estándar relativa del método cae con un rango de la mitad al doble del valor estimado, entonces es aceptable para su uso por analistas en diferentes laboratorios. El porcentaje de desviación estándar relativa para un solo analista debería ser de la mitad a dos tercios de la desviación estándar relativa para la variabilidad entre analistas.

Para obtener detalles sobre la Ecuación\ ref {14.11}, véase (a) Horwitz, W. Anal. Chem. 1982, 54, 67A—76A; b) Hall, P.; Selinger, B. Anal. Chem. 1989, 61, 1465—1466; c) Albert, R.; Horwitz, W. Anal. Chem. 1997, 69, 789—790, (d) “La increíble función de Horwitz”, Resumen Técnico AMC 17, julio de 2004; (e) Lingser, T. P. J. Tendencias Anal. Chem. 2006, 25, 1125. Para una discusión de las limitaciones de la ecuación, véase Linsinger, T. P. J.; Josephs, R. D. “Limitaciones de la aplicación de la ecuación de Horwitz”, Trends Anal. Chem. 2006, 25, 1125—1130, así como una refutación (Thompson, M. “Limitaciones de la aplicación de la ecuación de Horwitz: una refutación”, Trends Anal. Chem. 2007, 26, 659—661) y respuesta a la refutación (Linsinger, T. P. J.; Josephs, R. D. “Responder a la refutación del profesor Michael Thompson”, Tendencias Anal. Chem. 2007, 26, 662—663.