16.2: Propagación de la incertidumbre

En el Capítulo 4 consideramos los detalles matemáticos básicos de una propagación de la incertidumbre, limitando nuestro tratamiento a la propagación del error de medición. Este tratamiento es incompleto porque omite otras fuentes de incertidumbre que contribuyen a la incertidumbre general en nuestros resultados. Consideremos, por ejemplo, el Ejercicio 4.3.1, en el que determinamos la incertidumbre en una solución estándar de Cu ^{2 +} preparada disolviendo una masa conocida de alambre de Cu con HNO ₃, diluyendo a volumen en un matraz aforado de 500 mL, y luego diluyendo una porción de 1 mL de este solución madre a volumen en un matraz aforado de 250 ml. Para calcular la incertidumbre general se incluyó la incertidumbre en el pesaje de la muestra y la incertidumbre en el uso de la cristalería volumétrica. No se consideraron otras fuentes de incertidumbre, incluyendo la pureza del alambre de Cu, el efecto de la temperatura en la cristalería volumétrica y la repetibilidad de nuestras mediciones. En este apéndice damos una mirada más detallada a la propagación de la incertidumbre, utilizando como ejemplo la estandarización de NaOH.

Estandarización de una solución de NaOH

Debido a que el NaOH sólido es un material impuro, no podemos preparar directamente una solución madre pesando una muestra de NaOH y diluyendo al volumen. En cambio, determinamos la concentración de la solución a través de un proceso llamado estandarización. Un procedimiento bastante típico es utilizar la solución de NaOH para valorar una muestra cuidadosamente pesada de hidrógeno ftalato de potasio previamente secado, C ₈ H ₅ O ₄ K, que escribiremos aquí, en notación taquigráfica, como KHP. Por ejemplo, después de preparar una solución nominalmente 0.1 M de NaOH, colocamos una muestra de 0.4-g de KHP seca pesada con precisión en el recipiente de reacción de un valorador automático y la disolvemos en aproximadamente 50 mL de agua (la cantidad exacta de agua no es importante). El valorador automático agrega el NaOH a la solución de KHP y registra el pH en función del volumen de NaOH. La curva de titulación resultante nos proporciona el volumen de NaOH necesario para alcanzar el punto final de la titulación.

El siguiente ejemplo está adaptado de Ellison, S. L. R.; Rosslein, M.; Williams, A. Guía EURACHEM/CITAC: Cuantifying Uncertainty in Analytical Measurement, 3nd Edition, 2012. Consulte el Capítulo 5 para obtener más detalles sobre las estandarizaciones y consulte el Capítulo 9 para obtener más detalles sobre las titulaciones.

El punto final de la titulación es el volumen de NaOH que corresponde a la reacción estequiométrica entre NaOH y KHP.

\[\ce{NaOH}(aq) + \ce{C8H5O4K}(aq) \ce{->} \ce{C8H4O4^{2-}}(aq) + \ce{K+}(aq) + \ce{Na+}(aq) + \ce{H2O}(l) \nonumber\]

Conociendo la masa de KHP y el volumen de NaOH necesario para alcanzar el punto final, se utiliza la siguiente ecuación para calcular la molaridad de la solución de NaOH.

\[C_\ce{NaOH} = \frac {1000 \times m_\ce{KHP} \times P_\ce{KHP}} {FW_\ce{KHP} \times V_\ce{NaOH}} \nonumber\]

donde C _NaOH es la concentración de NaOH (en mol KHP/L), m _KHP es la masa de KHP tomada (en g), P _KHP es la pureza del KHP (donde P _KHP = 1 significa que el KHP es puro y no tiene impurezas), FW _KHP es la masa molar de KHP (en g KHP/mol KHP), y V _NaOH es el volumen de NaOH (en mL). El factor de 1000 simplemente convierte el volumen en mL a L.

Identificar y analizar las fuentes de incertidumbre

Aunque parece sencillo, identificar las fuentes de incertidumbre requiere cuidados, ya que es fácil pasar por alto fuentes importantes de incertidumbre. Un enfoque es usar un diagrama de causa y efecto, también conocido como diagrama de Ishikawa, llamado así por su inventor, Kaoru Ishikawa, o un diagrama de espina de pescado. Para construir un diagrama de causa y efecto, primero dibujamos una flecha que apunta al resultado deseado; este es el tronco del diagrama. Luego agregamos cinco ramificaciones principales al tronco, una para cada uno de los cuatro parámetros que determinan la concentración de NaOH (m _KHP, P _KHP, FW _KHP y V _NaOH) y otra para la repetibilidad del método, R. A continuación agregamos sucursales adicionales a la rama principal para cada uno de estos cinco factores, continuando hasta dar cuenta de todas las fuentes potenciales de incertidumbre. La Figura 16.2.1 muestra el diagrama completo de causa y efecto para este análisis.

Figura 16.2.1 : Diagrama de causa y efecto para la estandarización de NaOH por valoración frente a KHP. El tronco, mostrado en negro, representa la concentración de NaOH. Las flechas restantes representan las fuentes de incertidumbre que afectan a C _NaOH. Las flechas azules, por ejemplo, representan las principales fuentes de incertidumbre que afectan al _NaOH C, y las flechas verdes representan fuentes secundarias de incertidumbre que afectan a las fuentes primarias de incertidumbre. Consulte el texto para obtener más detalles.

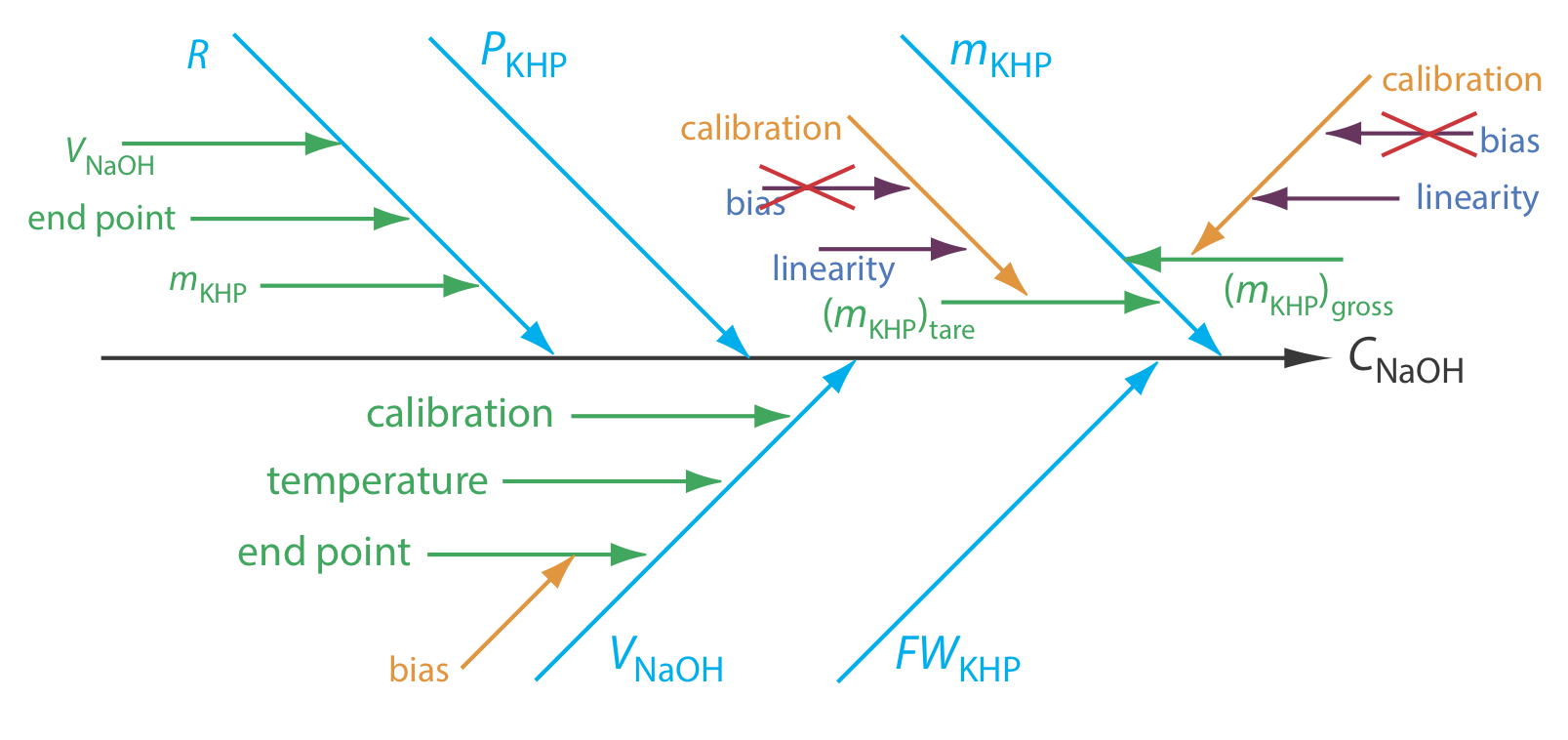
Antes de continuar, echemos un vistazo más de cerca a la Figura 16.2.1 para asegurarnos de que entendemos cada rama del diagrama. Para determinar la masa de KHP, m _KHP, realizamos dos mediciones: tarar la balanza y pesar la muestra bruta. Cada una de estas mediciones está sujeta a una incertidumbre de calibración. Cuando calibramos una balanza, esencialmente estamos creando una curva de calibración de la señal de la balanza en función de la masa. Cualquier curva de calibración está sujeta a una incertidumbre en la intersección y (sesgo) y una incertidumbre en la pendiente (linealidad). Podemos ignorar el sesgo de calibración porque contribuye igualmente tanto a la tara _bruta (m _KHP) como a la _tara (m _KHP), y porque determinamos la masa de KHP por diferencia.

\[m_\ce{KHP} = \left( m_\ce{KHP} \right)_\text{gross} - \left( m_\ce{KHP} \right)_\text{tare} \nonumber\]

El volumen de NaOH, V _NaOH, en el punto final tiene tres fuentes de incertidumbre. Primero, un valorador automatizado utiliza un pistón para suministrar NaOH al recipiente de reacción, lo que significa que el volumen de NaOH está sujeto a una incertidumbre en la calibración del pistón. Segundo, debido a que el volumen de una solución varía con la temperatura, existe una fuente adicional de incertidumbre debido a cualquier fluctuación en la temperatura ambiente durante el análisis. Finalmente, existe un sesgo en el punto final de la titulación si el NaOH reacciona con cualquier especie que no sea el KHP.

La repetibilidad, R, es una medida de cuán consistentemente podemos repetir el análisis. Cada instrumento que utilizamos, el balance y el valorador automatizado, contribuye a esta incertidumbre. Además, nuestra capacidad para detectar consistentemente el punto final también contribuye a la repetibilidad. Finalmente, no hay factores secundarios que afecten la incertidumbre de la pureza del KHP, P _KHP, o su masa molar, FW _KHP.

Estimación de la Desviación Estándar para Mediciones

Para completar una propagación de la incertidumbre debemos expresar la incertidumbre de cada medición de la misma manera, generalmente como una desviación estándar. Medir la desviación estándar para cada medición requiere tiempo y no siempre es práctico. Afortunadamente, la mayor parte de la fabricación proporciona un rango de tolerancia para cristalería e instrumentos. Una cristalería volumétrica de 100 mL, por ejemplo, tiene una tolerancia de\(\pm 0.1 \text{ mL}\) a una temperatura de 20 ^o C. Podemos convertir un rango de tolerancia a una desviación estándar utilizando uno de los siguientes tres enfoques.

Asumir una distribución uniforme

La figura 16.2.2 a muestra una distribución uniforme entre los límites de\(\pm x\), en la que cada resultado entre los límites es igualmente probable. Una distribución uniforme es la elección cuando el fabricante proporciona un rango de tolerancia sin especificar un nivel de confianza y cuando no hay razón para creer que los resultados cerca del centro del rango son más probables que los resultados en los extremos del rango. Para una distribución uniforme la desviación estándar estimada, s, es

\[s = \frac {x} {\sqrt{3}} \nonumber\]

Esta es la estimación más conservadora de la incertidumbre ya que da la estimación más grande para la desviación estándar.

Figura 16.2.2 : Tres distribuciones posibles para estimar la desviación estándar de un rango: (a) una distribución uniforme; (b) una distribución triangular; y (c) una distribución normal.

Asumir una distribución triangular

La figura 16.2.2 b muestra una distribución triangular entre los límites de\(\pm x\), en la que el resultado más probable está en el centro de la distribución, disminuyendo linealmente hacia cada límite. Una distribución triangular es la elección cuando el fabricante proporciona un rango de tolerancia sin especificar un nivel de confianza y cuando hay una buena razón para creer que los resultados cerca del centro del rango son más probables que los resultados en los extremos del rango. Para una distribución triangular la desviación estándar estimada, s, es

\[s = \frac {x} {\sqrt{6}} \nonumber\]

Esta es una estimación menos conservadora de la incertidumbre ya que, para cualquier valor de x, la desviación estándar es menor que la de una distribución uniforme.

Asumir una distribución normal

La figura 16.2.2 c muestra una distribución normal que se extiende, como debe, más allá de los límites de\(\pm x\), y que se centra en el punto medio entre — x y + x. Una distribución normal es la elección cuando conocemos el intervalo de confianza para el rango. Para una distribución normal la desviación estándar estimada, s, es

\[s = \frac {x} {z} \nonumber\]

donde z es 1.96 para un intervalo de confianza del 95% y 3.00 para un intervalo de confianza del 99.7%.

Completar la propagación de la incertidumbre

Ahora estamos listos para volver a nuestro ejemplo y determinar la incertidumbre para la estandarización de NaOH. Primero establecemos la incertidumbre para cada una de las cinco fuentes primarias: la masa de KHP, el volumen de NaOH en el punto final, la pureza del KHP, la masa molar para KHP y la repetibilidad de la titulación. Habiéndolos establecido, podemos combinarlos para llegar a la incertidumbre final.

Incertidumbre en la masa de KHP

Después de secar el KHP, lo almacenamos en un recipiente sellado para evitar que readsorba la humedad. Para encontrar la masa de KHP primero pesamos el recipiente, obteniendo un valor de 60.5450 g, y luego pesamos el recipiente después de retirar una porción de KHP, obteniendo un valor de 60.1562 g. La masa de KHP, por lo tanto, es 60.5450 — 60.1562 = 0.3888 g, o 388.8 mg.

Para encontrar la incertidumbre en esta masa se examina el certificado de calibración de la balanza, lo que indica que su tolerancia a la linealidad es\(\pm 0.15 \text{ mg}\). Asumiremos una distribución uniforme porque no hay razón para creer que cualquier resultado dentro de este rango sea más probable que cualquier otro resultado. Nuestra estimación de la incertidumbre para cualquier medición única de masa, u (m), es

\[u(m) = \frac {0.15 \text{ mg}} {\sqrt{3}} = \pm 0.087 \text{ mg} \nonumber\]

Debido a que determinamos la masa de KHP restando la masa final del contenedor de su masa inicial, la incertidumbre en la masa de KHP u (m _KHP), viene dada por la siguiente propagación de incertidumbre.

\[u(m_{\text{KHP}}) = \sqrt{\left( 0.087 \text{ mg} \right)^2 + \left( 0.087 \text{ mg} \right)^2} =\pm 0.12 \text{ mg} \nonumber\]

Incertidumbre en el volumen de NaOH

Después de colocar la muestra de KHP en el recipiente de reacción del valorador automatizado y disolver el KHP con agua, completamos la titulación y encontramos que se necesitan 18.64 mL de NaOH para llegar al punto final. Para encontrar la incertidumbre en este volumen debemos considerar, como se muestra en la Figura 16.2.1 , tres fuentes de incertidumbre: la calibración automatizada del valorador, la temperatura ambiente y cualquier sesgo en la determinación del punto final.

Para encontrar la incertidumbre de la calibración del valorador automatizado, examinamos el certificado del instrumento, que indica un rango de\(\pm 0.03 \text{ mL}\) para un pistón de 20 ml. Debido a que esperamos que un proceso de fabricación efectivo tenga más probabilidades de producir un pistón que opere cerca del centro de este rango que en los extremos, asumiremos una distribución triangular. Nuestra estimación de la incertidumbre debida a la calibración, u (V _cal) es

\[u(V_\text{cal}) = \frac {0.03 \text{ mL}} {\sqrt{6}} = \pm 0.012 \text{ mL} \nonumber\]

Para determinar la incertidumbre por la falta de control de temperatura, nos basamos en nuestro trabajo previo en el laboratorio, el cual ha establecido una variación de temperatura\(\pm 3 \text{°C}\) con un nivel de confianza del 95%. Para encontrar la incertidumbre, convertimos el rango de temperatura en un rango de volúmenes utilizando el coeficiente de expansión del agua

\[(2.1 \times 10^{-4} \text{°C}) \times (\pm 3 \text{°C}) \times 18.64 \text{ mL} = \pm 0.012 \text{ mL} \nonumber\]

y luego estimar la incertidumbre debida a la temperatura, u (V _temp) como

\[u(V_\text{temp}) = \frac {\pm 0.012 \text{ mL}} {1.96} = \pm 0.006 \text{ mL} \nonumber\]

Las titulaciones con NaOH están sujetas a un sesgo debido a la adsorción de CO ₂, que puede reaccionar con OH ^—, como se muestra aquí.

\[\ce{CO2}(aq) + \ce{2OH-}(aq) \ce{->} \ce{CO3^{2-}}(aq) + \ce{H2O}(l) \nonumber\]

Si está presente CO ₂, el volumen de NaOH en el punto final incluye tanto el NaOH que reacciona con el KHP como el NaOH que reacciona con CO ₂. En lugar de intentar estimar este sesgo, es más fácil bañar el recipiente de reacción en una corriente de argón, lo que excluye el CO ₂ del recipiente de reacción del valorador automático.

Sumando las incertidumbres para la calibración del pistón y la temperatura del laboratorio da la incertidumbre en la incertidumbre en el volumen de NaOH, u (V _NaOH) como

\[u(V_\ce{NaOH}) = \sqrt{(0.012 \text{ mL})^2 + (0.006 \text{ mL})^2} = \pm 0.013 \text{ mL} \nonumber\]

Incertidumbre en la pureza de KHP

Según el fabricante, la pureza de KHP es\(100 \% \pm 0.05 \%\), o\(1.0 \pm 0.0005\). Suponiendo una distribución rectangular, reportamos la incertidumbre, u (P _KHP) como

\[u(P_\ce{KHP}) = \frac {\pm 0.0005} {\sqrt{3}} = \pm 0.00029 \nonumber\]

Incertidumbre en la masa molar de KHP

La masa molar de C ₈ H ₅ O ₄ K es 204.2212 g/mol, con base en los siguientes pesos atómicos: 12.0107 para carbono, 1.00794 para hidrógeno, 15.9994 para oxígeno y 39.0983 para potasio. Cada uno de estos pesos atómicos tiene una incertidumbre cotizada que podemos convertir a una incertidumbre estándar asumiendo una distribución rectangular, como se muestra aquí (los detalles de los cálculos se dejan a usted).

elemento	incertidumbre cotizada (por átomo)	incertidumbre estándar (por átomo)	número de átomos	incertidumbre total
carbono	\(\pm 0.008\)	\(\pm 0.00046\)	8	\(\pm 0.00368\)
hidrógeno	\(\pm 0.00007\)	\(\ 0.000040\)	5	\(\pm 0.00020\)
oxígeno	\(\pm 0.0003\)	\(\pm 0.00017\)	4	\(\pm 0.00068\)
potasio	\(\pm 0.0001\)	\(\pm 0.000058\)	1	\(\pm 0.000058\)

Sumando estas incertidumbres da la incertidumbre en la masa molar, u (M _KHP), como

\[u(FW_\ce{KHP}) = \sqrt{(0.00368)^2 + (0.00020)^2 + (0.00068)^2 + (0.0.000058)^2} = \pm 0.0037 \text{ g/mL} \nonumber\]

Incertidumbre en la repetibilidad de la titulación

Para estimar la incertidumbre por repetibilidad se completan cinco titulaciones, obteniendo los siguientes resultados para la concentración de NaOH: 0.1021 M, 0.1022 M, 0.1022 M, 0.1021 M y 0.1021 M. La desviación estándar relativa, s _rel, para estas titulaciones es

\[s_{rel} = \frac {s} {\overline{X}} = \frac {5.48 \times 10^{-5}} {0.1021} = \pm 0.0005 \nonumber\]

Si tratamos la repetibilidad ideal como 1.0, entonces la incertidumbre debida a la repetibilidad, u (R), es la desviación estándar relativa, o, en este caso, 0.0005.

Combinando las incertidumbres

En la siguiente tabla se resumen las cinco fuentes primarias de incertidumbre.

término	fuente	valor, x	incertidumbre, u (x)
\(m_\ce{KHP}\)	masa de KHP	0.3888 g	\(\pm 0.00012\)g
\(V_\ce{naOH}\)	volumen de NaOH en el punto final	18.64 mL	\(\pm 0.013\)mL
\(P_\ce{KHP}\)	pureza de KHP	1.0	\(\pm 0.00029\)
\(M_\ce{KHP}\)	masa molar de KHP	204.2212 g/mol	\(\pm 0.0037\)g/mol
\(R\)	repetibilidad	1.0	\(\pm 0.0005\)

Como se describió anteriormente, calculamos la concentración de NaOH utilizamos la siguiente ecuación, la cual está ligeramente modificada para incluir un término para la repetibilidad de la titulación, que, como se describió anteriormente, tiene un valor de 1.0.

\[C_\ce{NaOH} = \frac {1000 \times m_\ce{KHP} \times P_\ce{KHP}} {FW_\ce{KHP} \times V_\ce{NaOH}} \times R \nonumber\]

Usando los valores de nuestra tabla, encontramos que la concentración de NaOH es

\[C_\ce{NaOH} = \frac {1000 \times 0.3888 \times 1.0} {204.2212 \times 18.64} \times 1.0 = 0.1021 \text{ M} \nonumber\]

Debido a que el cálculo de _NaOH C incluye solo multiplicación y división, la incertidumbre en la concentración, u (C _NaOH) viene dada por la siguiente propagación de incertidumbre.

\[\frac {u(C_\ce{NaOH})} {C_\ce{NaOH}} = \frac {u(C_\ce{NaOH})} {0.1021} = \sqrt{\frac {(0.00012)^2} {(0.3888)^2} + \frac {(0.00029)^2} {(1.0)^2} + \frac {(0.0037)^2} {(204.2212)^2} + \frac {(0.013)^2} {(18.64)^2} + \frac {(0.0005)^2} {(1.0)^2}} \nonumber\]

Resolver para u (C _NaOH) da su valor as\(\pm 0.00010 \text{ M}\), que es la incertidumbre final para el análisis.

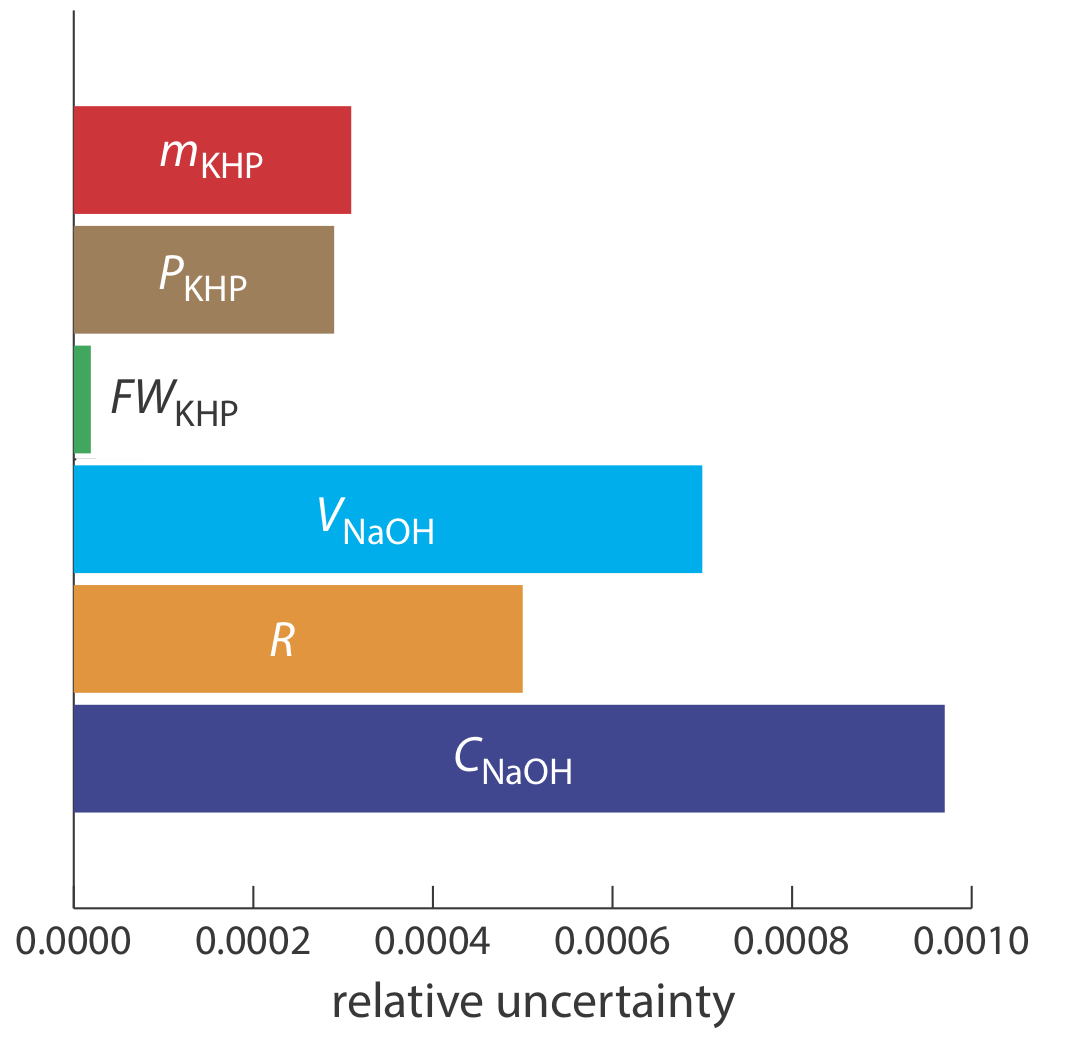
Evaluando las Fuentes de Incertidumbre

La figura 16.2.3 muestra la incertidumbre relativa en la concentración de NaOH y las incertidumbres relativas para cada una de las cinco contribuciones a la incertidumbre total. De las contribuciones, la más importante es el volumen de NaOH, y es aquí a donde debemos centrar nuestra atención si queremos mejorar la incertidumbre general para la estandarización.

Figura 16.2.3 : Gráfico de barras que muestra la incertidumbre relativa en _NaOH C, y la incertidumbre relativa en cada uno de los principales factores que afectan la incertidumbre general.