16.17: Revisión de Cinética Química
- Page ID
- 75480
La posición de equilibrio de una reacción define el grado en que puede ocurrir la reacción. Por ejemplo, se espera una reacción con una gran constante de equilibrio, como la disociación de HCl en agua
\[\ce{HCl}(aq) + \ce{H2O}(l) \ce{->} \ce{H3O+}(aq) + \ce{Cl-}(aq) \nonumber\]
para proceder casi a su finalización. Sin embargo, una gran constante de equilibrio no garantiza que una reacción alcance su posición de equilibrio. Muchas reacciones con grandes constantes de equilibrio, como la reducción\(\ce{MnO4-}\) de\(\ce{H2O}\)
\[\ce{4 MnO4-}(aq) + \ce{2 H2O}(l) \ce{->} \ce{4 MnO2}(s) + \ce{3 O2}(g) + \ce{4 OH-}(aq) \nonumber\]
no ocurran en una medida apreciable. El estudio de la velocidad a la que una reacción química se aproxima a su posición de equilibrio se denomina cinética.
Tasas de reacción química
Un estudio de la cinética de una reacción comienza con la medición de su velocidad de reacción. Consideremos, por ejemplo, la reacción general que se muestra a continuación, involucrando los solutos acuosos A, B, C y D, con estequiometrías de a, b, c y d.
\[a \ce{A} + b \ce{B} \ce{<=>} c \ce{C} + d \ce{D} \label{16.1}\]
La velocidad, o velocidad, a la que esta reacción se aproxima a su posición de equilibrio se determina siguiendo el cambio en la concentración de un reactivo o un producto en función del tiempo. Por ejemplo, si monitoreamos la concentración del reactivo A, expresamos la tasa como
\[R = - \frac {d[\ce{A}]} {dt} \label{16.2}\]
donde R es la tasa medida expresada como un cambio en la concentración de A en función del tiempo. Debido a que la concentración de un reactivo disminuye con el tiempo, incluimos un signo negativo para que la tasa tenga un valor positivo.
También podemos determinar la tasa siguiendo el cambio en la concentración de un producto en función del tiempo, que expresamos como
\[R^{\prime} = + \frac {d[\ce{C}]} {dt} \label{16.3}\]
Las tasas determinadas mediante el monitoreo de diferentes especies no necesariamente tienen el mismo valor. La tasa R en la Ecuación\ ref {16.2} y la tasa\(R^{\prime}\) en la Ecuación\ ref {16.3} tienen el mismo valor solo si los coeficientes estequiométricos de A y C en la reacción\ ref {16.1} son idénticos. En general, la relación entre las tasas R y\(R^{\prime}\) es
\[R = \frac {a} {c} \times R^{\prime} \nonumber\]
La Ley de Tarifas
Una ley de velocidad describe cómo la velocidad de una reacción se ve afectada por la concentración de cada especie en la mezcla de reacción. La ley de tarifas para Reacción\ ref {16.1} toma la forma general de
donde k es la constante de velocidad, y\(\alpha\)\(\beta\),\(\gamma\),\(\delta\), y\(\epsilon\) son los órdenes de reacción de la reacción para cada especie presente en la reacción.
Hay varios puntos importantes sobre la ley de tasas en la Ecuación\ ref {16.4}. Primero, la velocidad de una reacción puede depender de las concentraciones tanto de los reactivos como de los productos, así como de la concentración de una especie que no aparece en la estequiometría general de la reacción. La especie E en la Ecuación\ ref {16.4}, por ejemplo, puede ser un catalizador que no aparece en la estequiometría general de la reacción, pero que aumenta la velocidad de la reacción. Segundo, el orden de reacción para una especie dada no es necesariamente el mismo que su estequiometría en la reacción química. Los órdenes de reacción pueden ser positivos, negativos o cero, y pueden tomar valores enteros o no enteros. Finalmente, el orden general de reacción de la reacción es la suma de los órdenes de reacción individuales para cada especie. Así, el orden general de reacción para la Ecuación\ ref {16.4} es\(\alpha + \beta +\gamma + \delta + \epsilon\).
Análisis cinético de reacciones seleccionadas
En esta sección revisamos la aplicación de la cinética a varias reacciones químicas simples, enfocándonos en cómo podemos usar la forma integrada de la ley de velocidad para determinar los órdenes de reacción. Además, consideramos cómo podemos determinar la ley tarifaria para un sistema más complejo.
Reacciones de primer orden
El caso más simple que podemos tratar es una reacción de primer orden en la que la velocidad de la reacción depende de la concentración de una sola especie. El ejemplo más simple de una reacción de primer orden es una descomposición térmica irreversible de un solo reactivo, que representamos como
\[\ce{A} \ce{->} \text{products} \label{16.5}\]
con una ley de tarifas de
\[R = - \frac {d[\ce{A}]} {dt} = k[\ce{A}] \label{16.6}\]
La forma más sencilla de demostrar que una reacción es de primer orden en A, es duplicar la concentración de A y anotar el efecto sobre la velocidad de la reacción. Si la tasa observada se duplica, entonces la reacción es de primer orden en A. Alternativamente, podemos derivar una relación entre la concentración de A y el tiempo reordenando la Ecuación\ ref {16.6} e integrando.
\[\frac {d[\ce{A}]} {[\ce{A}]} = -kdt \nonumber\]
\[\int_{[{A}]_0}^{[{A}]_t}\frac{1}{[A]}d[A] = - k \int_{o}^{t}dt \label{16.7}\]
Evaluar las integrales en la Ecuación\ ref {16.7} y reorganizar
\[\ln \frac {[\ce{A}]_t} {[\ce{A}]_0} = -kt \label{16.8}\]
\[\ln [\ce{A}]_t = \ln [\ce{A}]_0 - kt \label{16.9}\]
muestra que para una reacción de primer orden, una gráfica de\(\ln[\ce{A}]_t\) versus tiempo es lineal con una pendiente de — k y una intercepción y de\(\ln[\ce{A}]_0\). La ecuación\ ref {16.8} y la ecuación\ ref {16.9} se conocen como formas integradas de la ley de tasas. Reacción\ ref {16.5} no es la única forma posible de reacción de primer orden. Por ejemplo, la reacción
\[\ce{A} + \ce{B} \ce{->} \text{products} \label{16.10}\]
seguirá una cinética de primer orden si la reacción es de primer orden en A y si la concentración de B no afecta la velocidad de la reacción, lo que puede ocurrir si el mecanismo de la reacción implica al menos dos etapas. Imagínese que en el primer paso, A se convierte lentamente en una especie intermedia, C, que reacciona rápidamente con el reactivo restante, B, en uno o más pasos, para formar los productos.
\[\ce{A} \ce{->} \ce{B} (\text{slow}) \nonumber\]
\[\ce{B} + \ce{C} \ce{->} \text{products} \nonumber\]
Debido a que la velocidad de una reacción depende solo de aquellas especies en el paso más lento, generalmente llamado paso determinante de la velocidad, y cualquier etapa anterior, la especie B no aparecerá en la ley de tasas.
Reacciones de segundo orden
La reacción más simple que demuestra un comportamiento de segundo orden es
\[\ce{2 A} \ce{->} \text{products} \nonumber\]
para lo cual la ley de tarifas es
\[R = - \frac {d[\ce{A}]} {dt} = k[\ce{A}]^2 \nonumber\]
Procediendo como hicimos antes para una reacción de primer orden, podemos derivar fácilmente la forma integrada de la ley tarifaria.
\[\frac {d[\ce{A}]} {[\ce{A}]^2} = -kdt \nonumber\]
\[\int_{[\ce{A}]_0}^{[\ce{A}]_t} = -k \int_0^t dt \nonumber\]
\[\frac {1} {[\ce{A}]_t} = kt + \frac {1} {[\ce{A}]_0} \nonumber\]
Para una reacción de segundo orden, por lo tanto, una gráfica de ([A] t) —1 versus t es lineal con una pendiente de k y una intercepción y de ([A] 0) —1. Alternativamente, podemos demostrar que una reacción es de segundo orden en A al observar el efecto sobre la velocidad cuando cambiamos la concentración de A. En este caso, duplicar la concentración de A produce un aumento de cuatro veces en la velocidad de la reacción.
Los siguientes datos se obtuvieron durante un estudio cinético de la hidratación de p-metoxifenilacetileno midiendo las cantidades relativas de reactivos y productos por RMN [datos de Kaufman, D,; Sterner, C.; Masek, B.; Svenningsen, R.; Samuelson, G. J. Chem. Educ. 1982, 59, 885—886].
| tiempo (min) | % p-metoxifenilacetileno |
|---|---|
| 67 | 85.9 |
| 161 | 70.0 |
| 241 | 57.6 |
| 381 | 40.7 |
| 479 | 32.4 |
| 545 | 27.7 |
| 604 | 24 |
Solución
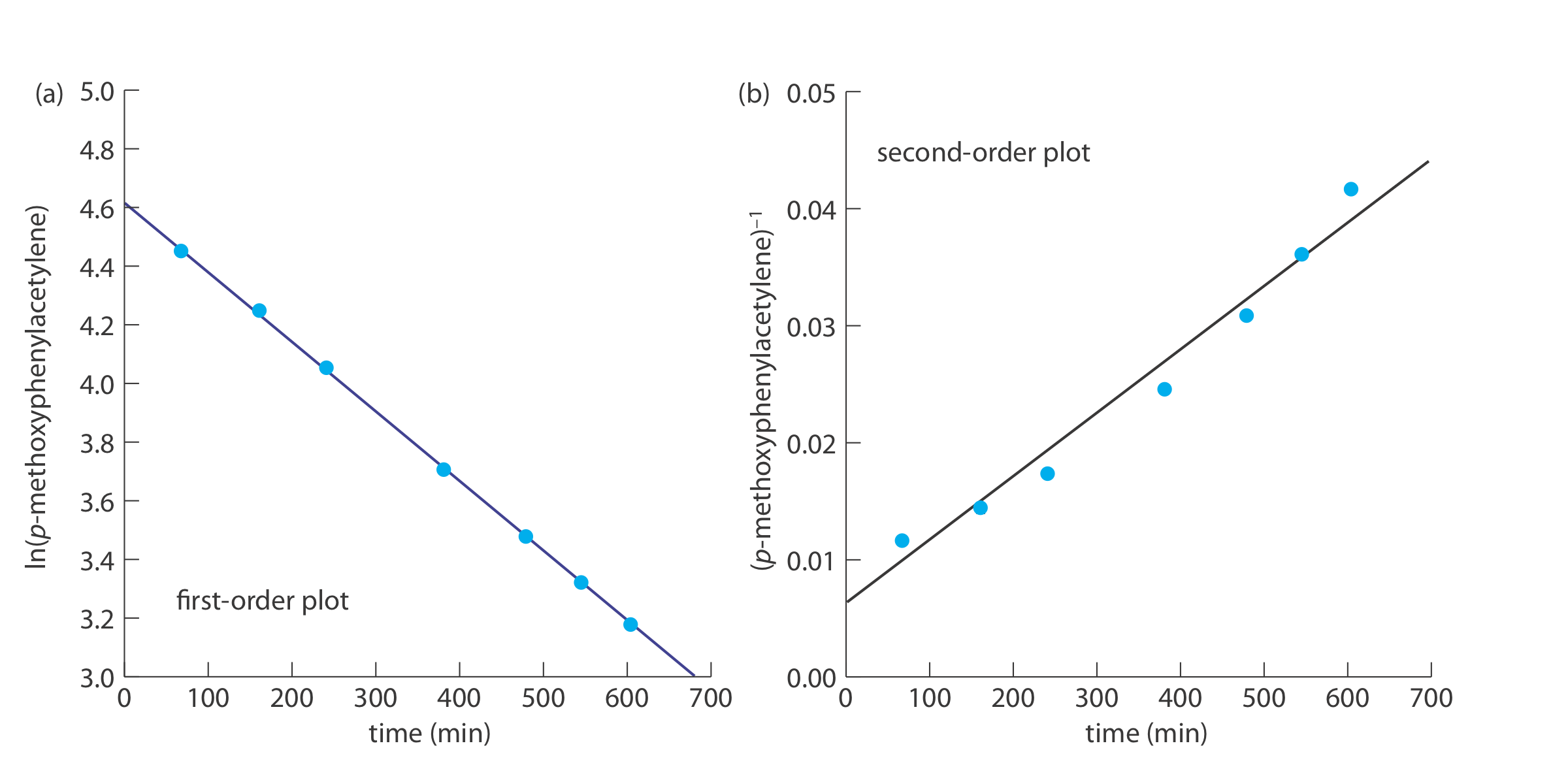
Para determinar el orden de la reacción representamos ln (%p-metoxifenilacetileno) versus tiempo para una reacción de primer orden, y (%p-metoxifenilacetileno) —1 versus tiempo para una reacción de segundo orden (ver abajo). Debido a que una línea recta para la gráfica de primer orden se ajusta perfectamente a los datos, concluimos que la reacción es de primer orden en p-met - oxifenilacetileno. Tenga en cuenta que cuando trazamos los datos usando la ecuación para una reacción de segundo orden, los datos muestran una curvatura que no se ajusta al modelo de línea recta.
Reacciones de Pseudo-Orden y Método de Tasas Iniciales
Desafortunadamente, la mayoría de las reacciones de importancia en la química analítica no siguen las simples leyes de tasa de primer orden o segundo orden discutidas anteriormente. Es más probable que nos encontremos con la ley de tasas de segundo orden dada en la Ecuación\ ref {16.11} que la de la Ecuación\ ref {16.10}.
\[R = k [\ce{A}] [\ce{B}] \label{16.11}\]
Demostrar que una reacción obedece a la ley tarifaria en la Ecuación\ ref {16.11} se complica por la falta de una forma simple integrada de la ley tarifaria. Muchas veces podemos simplificar la cinética realizando el análisis en condiciones donde las concentraciones de todas las especies menos una son tan grandes que sus concentraciones efectivamente permanecen constantes durante la reacción. Por ejemplo, si la concentración de B se selecciona de tal manera que\([\ce{B}] >> [\ce{A}]\), entonces la Ecuación\ ref {16.11} simplifica a
\[R = k^{\prime} [\ce{A}] \nonumber\]
donde la constante de velocidad k ́ es igual a k [B]. Bajo estas condiciones, la reacción parece seguir una cinética de primer orden en A; por esta razón identificamos la reacción como pseudo-primer orden en A. Podemos verificar el orden de reacción para A usando la ley de velocidad integrada o observando el efecto sobre la velocidad de la reacción de cambiar la concentración de A. Para encontrar el orden de reacción para B, repetimos el proceso bajo condiciones donde\([\ce{A}] >> [\ce{B}]\).
Una variación en el uso de reacciones pseudo-ordenadas es el método de velocidad inicial. En este enfoque realizamos una serie de experimentos en los que cambiamos una a la vez la concentración de cada especie que podría afectar la velocidad de reacción y medir la velocidad inicial resultante. Comparar la velocidad inicial de la reacción para dos experimentos en los que solo la concentración de una especie es diferente, nos permite determinar el orden de reacción para esa especie. La aplicación de este método se esboza en el siguiente ejemplo.
Los siguientes datos se recolectaron durante un estudio cinético de la yodación de acetona midiendo la concentración de I 2 sin reaccionar en solución [datos de Birk, J. P.; Walters, D. L. J. Chem. Educ. 1992, 69, 585—587].
| número de experimento | \([\ce{C3H6O}]\)(M) | \([\ce{H3O+}]\)(M) | \([\ce{I2}]\)(M) | Tarifa (M s —1) |
|---|---|---|---|---|
| 1 | \ ([\ ce {C3H6O}]\) (M) ">1.33 | \ ([\ ce {H3O+}]\) (M) ">0.0404 | \ ([\ ce {I2}]\) (M) ">\(6.65 \times 10^{-3}\) | \(1.78 \times 10^{-6}\) |
| 2 | \ ([\ ce {C3H6O}]\) (M) ">1.33 | \ ([\ ce {H3O+}]\) (M) ">0.0809 | \ ([\ ce {I2}]\) (M)” class="lt-chem-135884">
\(6.65 \times 10^{-3}\) |
\(3.89 \times 10^{-6}\) |
| 3 | \ ([\ ce {C3H6O}]\) (M) ">1.33 | \ ([\ ce {H3O+}]\) (M) ">0.162 | \ ([\ ce {I2}]\) (M) ">\(6.65 \times 10^{-3}\) | \(8.11 \times 10^{-6}\) |
| 4 | \ ([\ ce {C3H6O}]\) (M) ">1.33 | \ ([\ ce {H3O+}]\) (M) ">0.323 | \ ([\ ce {I2}]\) (M) ">\(6.65 \times 10^{-3}\) | \(1.66 \times 10^{-5}\) |
| 5 | \ ([\ ce {C3H6O}]\) (M) ">0.167 | \ ([\ ce {H3O+}]\) (M) ">0.323 | \ ([\ ce {I2}]\) (M) ">\(6.65 \times 10^{-3}\) | \(1.64 \times 10^{-6}\) |
| 6 | \ ([\ ce {C3H6O}]\) (M) ">0.333 | \ ([\ ce {H3O+}]\) (M) ">0.323 | \ ([\ ce {I2}]\) (M) ">\(6.65 \times 10^{-3}\) | \(3.76 \times 10^{-6}\) |
| 7 | \ ([\ ce {C3H6O}]\) (M) ">0.667 | \ ([\ ce {H3O+}]\) (M) ">0.323 | \ ([\ ce {I2}]\) (M) ">\(6.65 \times 10^{-3}\) | \(7.55 \times 10^{-6}\) |
| 8 | \ ([\ ce {C3H6O}]\) (M) ">0.333 | \ ([\ ce {H3O+}]\) (M) ">0.323 | \ ([\ ce {I2}]\) (M) ">\(3.32 \times 10^{-3}\) | \(3.57 \times 10^{-6}\) |
Solución
El orden de la ley de velocidad con respecto a los tres reactivos se determina comparando las velocidades de dos experimentos en los que hay un cambio en la concentración para solo uno de los reactivos. Por ejemplo, en los Experimentos 1 y 2, solo los\([\ce{H3O+}]\) cambios; al\([\ce{H3O+}]\) duplicar el doble de la tasa, sabemos que la reacción es de primer orden en\(\ce{H3O+}\). Trabajando de la misma manera, los Experimentos 6 y 7 muestran que la reacción también es de primer orden con respecto a\([\ce{C3H6O}]\), y los Experimentos 6 y 8 muestran que la velocidad de la reacción es independiente de la\([\ce{I2}]\). Así, la ley de tarifas es
\[R = k [\ce{C3H6O}] [\ce{H3O+}] \nonumber\]
Para determinar el valor de la constante de tasa, sustituimos la tasa, la\([\ce{H3O+}]\), y la\([\ce{H3O+}]\) para cada experimento en la ley de tasa y resolvemos por k. El uso de los datos del Experimento 1, por ejemplo, da una constante de velocidad de\(3.31 \times 10^{-5} \text{ M}^{-1} \text{ s}^{-1}\). La constante de velocidad promedio para los ocho experimentos es\(3.49 \times 10^{-5} \text{ M}^{-1} \text{ s}^{-1}\).