Saltar al contenido principal
LibreTexts Español

8.2: Regresión lineal ponderada con errores en y

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    69361

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Nuestro tratamiento de la regresión lineal a este punto asume que cualquier error indeterminado que afecte a y es independiente del valor de x. Si esta suposición es falsa, entonces debemos incluir la varianza para cada valor de y en nuestra determinación de la intersección y, b 0, y la pendiente, b 1; así

    \[b_0 = \frac {\sum_{i = 1}^{n} w_i y_i - b_1 \sum_{i = 1}^{n} w_i x_i} {n} \nonumber \]

    \[b_1 = \frac {n \sum_{i = 1}^{n} w_i x_i y_i - \sum_{i = 1}^{n} w_i x_i \sum_{i = 1}^{n} w_i y_i} {n \sum_{i =1}^{n} w_i x_i^2 - \left( \sum_{i = 1}^{n} w_i x_i \right)^2} \nonumber\]

    donde w i es un factor de ponderación que da cuenta de la varianza en y i

    \[w_i = \frac {n (s_{y_i})^{-2}} {\sum_{i = 1}^{n} (s_{y_i})^{-2}} \nonumber\]

    y\(s_{y_i}\) es la desviación estándar para y i. En una regresión lineal ponderada, la contribución de cada par xy a la línea de regresión es inversamente proporcional a la precisión de y i; es decir, cuanto más preciso sea el valor de y, mayor será su contribución a la regresión.

    Ejemplo\(\PageIndex{4}\)

    Aquí se muestran datos para una estandarización externa en la que s std es la desviación estándar para la determinación de tres réplicas de la señal. Se trata de los mismos datos utilizados en los ejemplos de la Sección 8.1 con información adicional sobre las desviaciones estándar en la señal.

    \(C_{std}\)(unidades arbitrarias) \(S_{std}\)(unidades arbitrarias) \(s_{std}\)
    \ (C_ {std}\) (unidades arbitrarias) ">0.000 \ (S_ {std}\) (unidades arbitrarias) ">0.00 \ (s_ {std}\) ">0.02
    \ (C_ {std}\) (unidades arbitrarias) ">0.100 \ (S_ {std}\) (unidades arbitrarias) ">12.36 \ (s_ {std}\) ">0.02
    \ (C_ {std}\) (unidades arbitrarias) ">0.200 \ (S_ {std}\) (unidades arbitrarias) ">24.83 \ (s_ {std}\) ">0.07
    \ (C_ {std}\) (unidades arbitrarias) ">0.300 \ (S_ {std}\) (unidades arbitrarias) ">35.91 \ (s_ {std}\) ">0.13
    \ (C_ {std}\) (unidades arbitrarias) ">0.400 \ (S_ {std}\) (unidades arbitrarias) ">48.79 \ (s_ {std}\) ">0.22
    \ (C_ {std}\) (unidades arbitrarias) ">0.500 \ (S_ {std}\) (unidades arbitrarias) ">60.42 \ (s_ {std}\) ">0.33

    Determinar la ecuación de la curva de calibración usando una regresión lineal ponderada. Al trabajar a través de este ejemplo, recuerde que x corresponde a C std, y que y corresponde a S std.

    Solución

    Comenzamos configurando una tabla para ayudar en el cálculo de los factores de ponderación.

    \(C_{std}\)(unidades arbitrarias) \(S_{std}\)(unidades arbitrarias) \(s_{std}\) \((s_{y_i})^{-2}\) \(w_i\)
    \ (C_ {std}\) (unidades arbitrarias) ">0.000 \ (S_ {std}\) (unidades arbitrarias) ">0.00 \ (s_ {std}\) ">0.02 \ ((s_ {y_i}) ^ {-2}\) ">2500.00 \ (w_i\) ">2.8339
    \ (C_ {std}\) (unidades arbitrarias) ">0.100 \ (S_ {std}\) (unidades arbitrarias) ">12.36 \ (s_ {std}\) ">0.02 \ ((s_ {y_i}) ^ {-2}\) ">250,00 \ (w_i\) ">2.8339
    \ (C_ {std}\) (unidades arbitrarias) ">0.200 \ (S_ {std}\) (unidades arbitrarias) ">24.83 \ (s_ {std}\) ">0.07 \ ((s_ {y_i}) ^ {-2}\) ">204.08 \ (w_i\) ">0.2313
    \ (C_ {std}\) (unidades arbitrarias) ">0.300 \ (S_ {std}\) (unidades arbitrarias) ">35.91 \ (s_ {std}\) ">0.13 \ ((s_ {y_i}) ^ {-2}\) ">59.17 \ (w_i\) ">0.0671
    \ (C_ {std}\) (unidades arbitrarias) ">0.400 \ (S_ {std}\) (unidades arbitrarias) ">48.79 \ (s_ {std}\) ">0.22 \ ((s_ {y_i}) ^ {-2}\) ">20.66 \ (w_i\) ">0.0234
    \ (C_ {std}\) (unidades arbitrarias) ">0.500 \ (S_ {std}\) (unidades arbitrarias) ">60.42 \ (s_ {std}\) ">0.33 \ ((s_ {y_i}) ^ {-2}\) ">9.18 \ (w_i\) ">0.0104

    Sumando los valores en la cuarta columna da

    \[\sum_{i = 1}^{n} (s_{y_i})^{-2} \nonumber\]

    que utilizamos para calcular los pesos individuales en la última columna. Como comprobación de sus cálculos, la suma de los pesos individuales debe ser igual al número de estándares de calibración, n. La suma de las entradas en la última columna es de 6.0000, así que todo está bien. Después de calcular los pesos individuales, utilizamos una segunda tabla para ayudar en el cálculo de los cuatro términos de suma en las ecuaciones para la pendiente\(b_1\),, y la intersección y,\(b_0\).

    \(x_i\) \(y_i\) \(w_i\) \(w_i x_i\) \(w_i y_i\) \(w_i x_i^2\) \(w_i x_i y_i\)
    \ (x_i\) ">0.000 \ (y_i\) ">0.00 \ (w_i\) ">2.8339 \ (w_i x_i\) ">0.0000 \ (w_i y_i\) ">0.0000 \ (w_i x_i^2\) ">0.0000 \ (w_i x_i y_i\) ">0.0000
    \ (x_i\) ">0.100 \ (y_i\) ">12.36 \ (w_i\) ">2.8339 \ (w_i x_i\) ">0.2834 \ (w_i y_i\) ">35.0270 \ (w_i x_i^2\) ">0.0283 \ (w_i x_i y_i\) ">3.5027
    \ (x_i\) ">0.200 \ (y_i\) ">24.83 \ (w_i\) ">0.2313 \ (w_i x_i\) ">0.0463 \ (w_i y_i\) ">5.7432 \ (w_i x_i^2\) ">0.0093 \ (w_i x_i y_i\) ">1.1486
    \ (x_i\) ">0.300 \ (y_i\) ">35.91 \ (w_i\) ">0.0671 \ (w_i x_i\) ">0.0201 \ (w_i y_i\) ">2.4096 \ (w_i x_i^2\) ">0.0060 \ (w_i x_i y_i\) ">0.7229
    \ (x_i\) ">0.400 \ (y_i\) ">48.79 \ (w_i\) ">0.0234 \ (w_i x_i\) ">0.0094 \ (w_i y_i\) ">1.1417 \ (w_i x_i^2\) ">0.0037 \ (w_i x_i y_i\) ">0.4567
    \ (x_i\) ">0.500 \ (y_i\) ">60.42 \ (w_i\) ">0.0104 \ (w_i x_i\) ">0.0052 \ (w_i y_i\) ">0.6284 \ (w_i x_i^2\) ">0.0026 \ (w_i x_i y_i\) ">0.3142

    Sumando los valores en las últimas cuatro columnas da

    \[\sum_{i = 1}^{n} w_i x_i = 0.3644 \quad \sum_{i = 1}^{n} w_i y_i = 44.9499 \quad \sum_{i = 1}^{n} w_i x_i^2 = 0.0499 \quad \sum_{i = 1}^{n} w_i x_i y_i = 6.1451 \nonumber\]

    que da la pendiente estimada y la intersección y estimada como

    \[b_1 = \frac {(6 \times 6.1451) - (0.3644 \times 44.9499)} {(6 \times 0.0499) - (0.3644)^2} = 122.985 \nonumber\]

    \[b_0 = \frac{44.9499 - (122.985 \times 0.3644)} {6} = 0.0224 \nonumber\]

    La ecuación de calibración es

    \[S_{std} = 122.98 \times C_{std} + 0.2 \nonumber\]

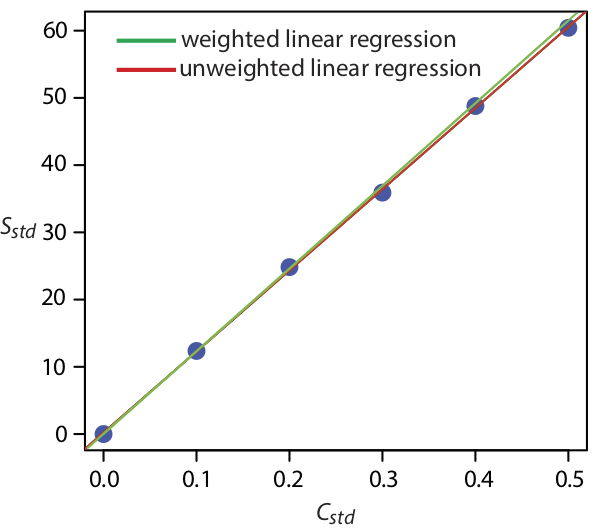
    La figura\(\PageIndex{1}\) muestra la curva de calibración para la regresión ponderada determinada aquí y la curva de calibración para la regresión no ponderada en la Sección 8.2. Aunque las dos curvas de calibración son muy similares, existen ligeras diferencias en la pendiente y en la intersección y. Lo más notable es que la intersección y para la regresión lineal ponderada está más cerca del valor esperado de cero. Debido a que la desviación estándar para la señal, S std, es menor para concentraciones más pequeñas de analito, C std, una regresión lineal ponderada da más énfasis a estos estándares, permitiendo una mejor estimación de la y -interceptar.

    Figura5.14.png
    Figura\(\PageIndex{1}\): Comparación de las curvas de calibración normal no ponderada y ponderada. Consulte Ejemplo\(\PageIndex{1}\) para obtener detalles de la regresión lineal no ponderada y Ejemplo\(\PageIndex{4}\) para obtener detalles de la regresión lineal ponderada.

    Las ecuaciones para calcular los intervalos de confianza para la pendiente, la intersección y y la concentración de analito cuando se utiliza una regresión lineal ponderada no son tan fáciles de definir como para una regresión lineal no ponderada [Bonate, P. J. Anal. Chem. 1993, 65, 1367—1372]. El intervalo de confianza para la concentración del analito, sin embargo, está en su valor óptimo cuando la señal del analito está cerca del centroide ponderado, y c, de la curva de calibración.

    \[y_c = \frac {1} {n} \sum_{i = 1}^{n} w_i x_i \nonumber\]

    8.2: Regresión lineal ponderada con errores en y is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by LibreTexts.