9.5: Modelos Matemáticos de Superficies de Respuesta
- Page ID
- 69244
Una superficie de respuesta se describe matemáticamente mediante una ecuación que relaciona la respuesta con sus factores. Si medimos la respuesta para varias combinaciones de niveles factoriales, entonces podemos usar un análisis de regresión para construir un modelo de la superficie de respuesta. Existen dos amplias categorías de modelos que podemos utilizar para un análisis de regresión: modelos teóricos y modelos empíricos.
Modelos teóricos de la superficie de respuesta
Un modelo teórico se deriva de las relaciones químicas y físicas conocidas entre la respuesta y sus factores. En espectrofotometría, por ejemplo, la ley de Beer es un modelo teórico que relaciona la absorbancia de un analito, A, con su concentración, C A
\[A = \epsilon b C_A \nonumber\]
donde\(\epsilon\) es la absortividad molar y b es la longitud de trayectoria de la radiación electromagnética que pasa a través de la muestra. Una curva de calibración de la ley de Beer, por lo tanto, es un modelo teórico de una superficie de respuesta. En el Capítulo 8 aprendimos a utilizar la regresión lineal para construir un modelo matemático basado en una relación teórica.
Modelos empíricos de la superficie de respuesta
En muchos casos se desconoce la relación teórica subyacente entre la respuesta y sus factores. Todavía podemos desarrollar un modelo de superficie de respuesta si hacemos algunas suposiciones razonables sobre la relación subyacente entre los factores y la respuesta. Por ejemplo, si creemos que los factores A y B son independientes y que cada uno solo tiene un efecto de primer orden en la respuesta, entonces la siguiente ecuación es un modelo adecuado.
\[R = \beta_0 + \beta_a A + \beta_b B \nonumber\]
donde R es la respuesta, A y B son los niveles de factores, y\(\beta_0\)\(\beta_a\), y\(\beta_b\) son parámetros ajustables cuyos valores están determinados por un análisis de regresión lineal. Otros ejemplos de ecuaciones incluyen aquellos para factores dependientes
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \nonumber\]
y aquellos con términos de orden superior.
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{aa} A^2 + \beta_{bb} B^2 \nonumber\]
Cada una de estas ecuaciones proporciona un modelo empírico de la superficie de respuesta porque no tiene bases rigurosas en una comprensión teórica de la relación entre la respuesta y sus factores. Aunque un modelo empírico puede proporcionar una excelente descripción de la superficie de respuesta en un rango limitado de niveles factoriales, no tiene base teórica y no podemos extenderla de manera confiable a partes inexploradas de la superficie de respuesta.
Diseños factoriales
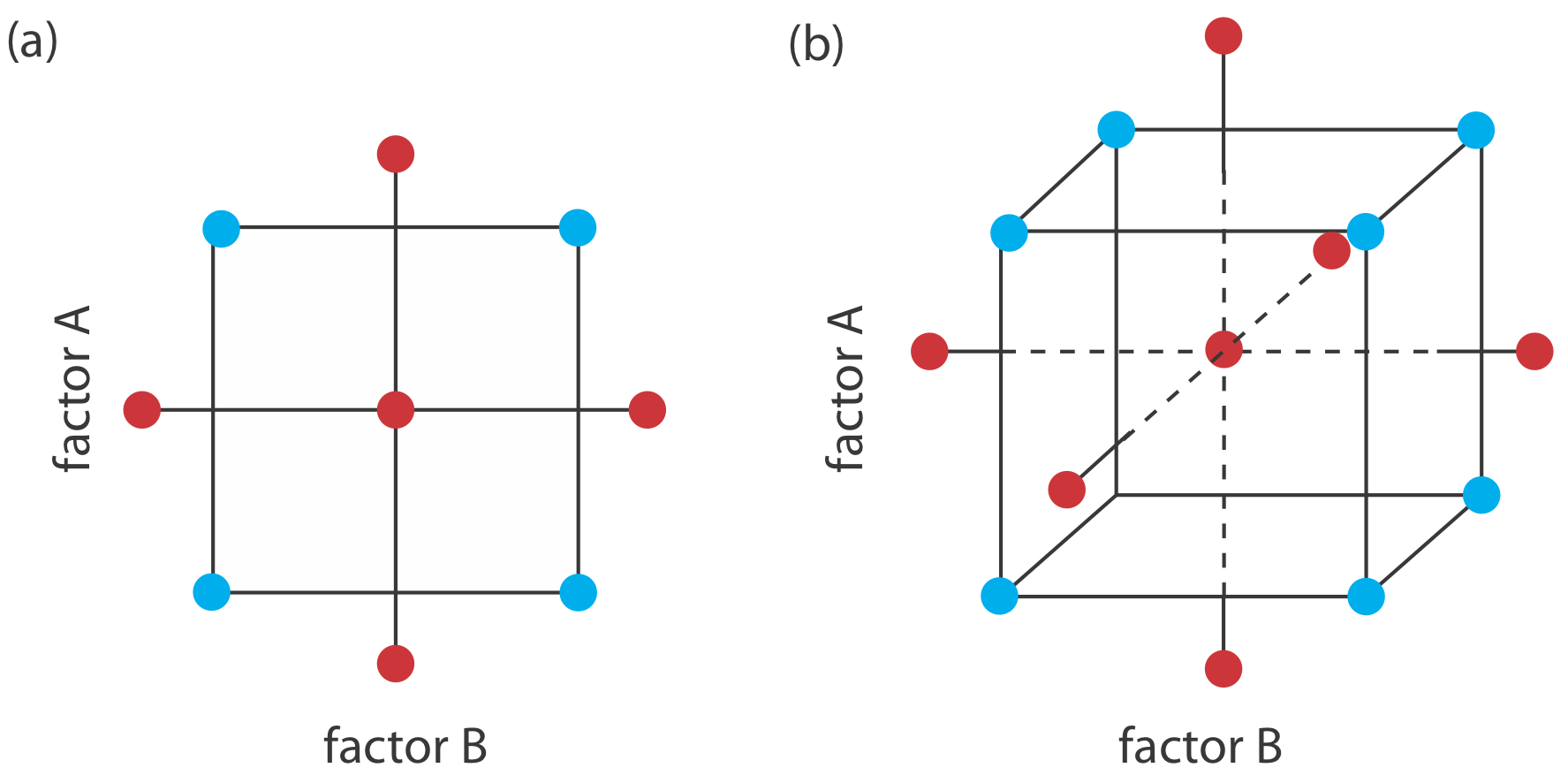
Para construir un modelo empírico medimos la respuesta para al menos dos niveles para cada factor. Por conveniencia etiquetamos estos niveles como alto, H f, y bajo, L f, donde f es el factor; así H A es el nivel alto para el factor A y L B es el nivel bajo para el factor B. Si nuestro modelo empírico contiene más de un factor, entonces el nivel alto de cada factor se empareja tanto con el nivel alto como con el nivel bajo para todos los demás factores. De la misma manera, el nivel bajo para cada factor se empareja con el nivel alto y el nivel bajo para todos los demás factores. Como se muestra en la Figura\(\PageIndex{1}\), esto requiere 2 k experimentos donde k es el número de factores. Este diseño experimental se conoce como un diseño factorial de 2 k.
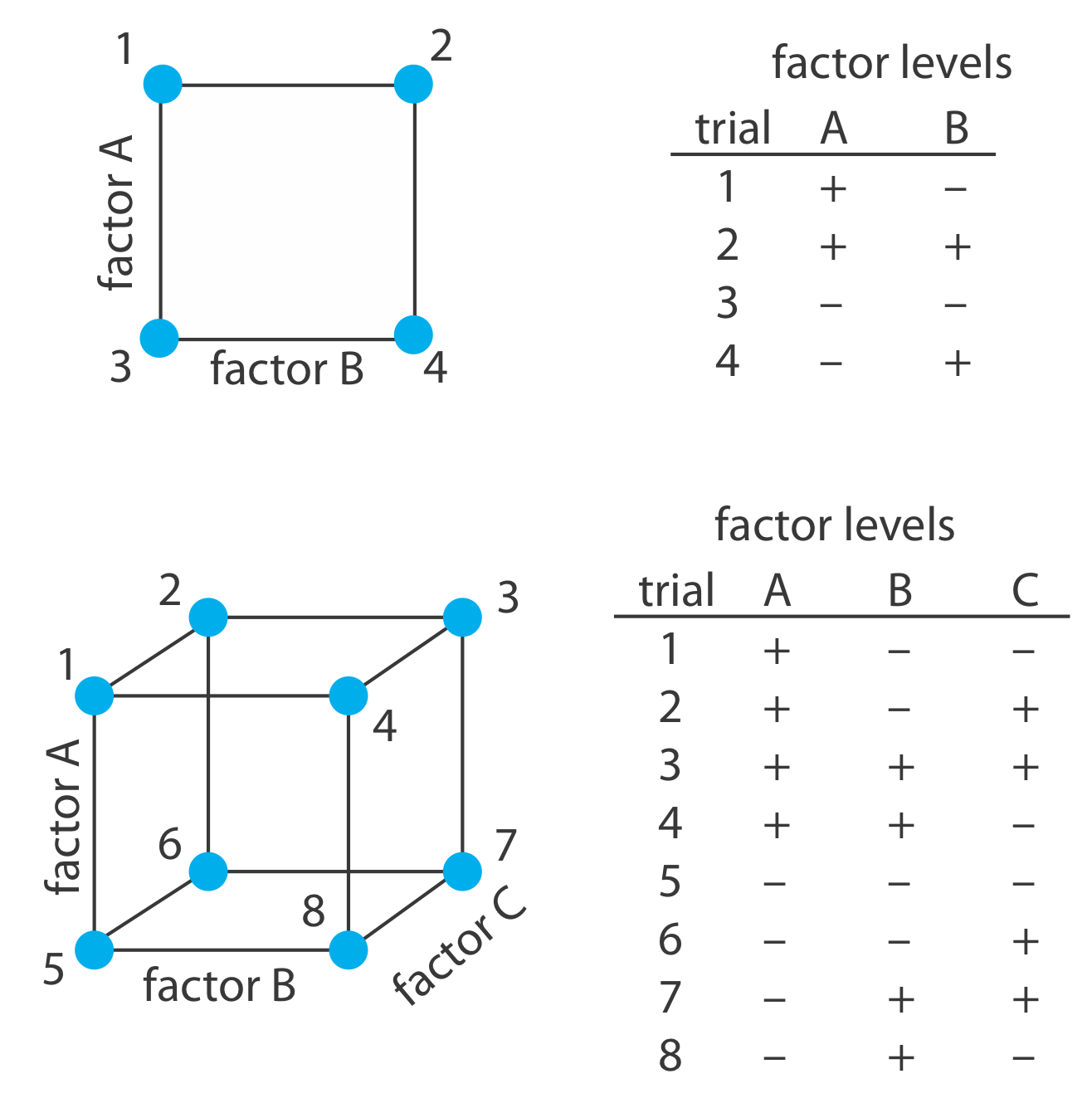
Otro sistema de notación es usar un signo más (+) para indicar el nivel alto de un factor y un signo menos (—) para indicar su nivel bajo.
Determinar el modelo empírico
Un diseño factorial 2 2 requiere cuatro experimentos y permite un modelo empírico con cuatro variables.
Con cuatro experimentos, podemos utilizar un diseño factorial 2 2 para crear un modelo empírico que incluye cuatro variables: una intercepción, efectos de primer orden en A y B, y un término de interacción entre A y B
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \nonumber \]
El siguiente ejemplo nos guía a través de los cálculos necesarios para encontrar este modelo.
Supongamos que deseamos optimizar el rendimiento de una síntesis y esperamos que la cantidad de catalizador (factor A con unidades de mM) y la temperatura (factor B con unidades de °C) sean probablemente factores importantes. La respuesta,\(R\), es el rendimiento de la reacción en mg. Realizamos cuatro experimentos y obtenemos las siguientes respuestas:
| correr | A | B | R |
|---|---|---|---|
| 1 | 15 | 20 | 145 |
| 2 | 25 | 20 | 158 |
| 3 | 15 | 30 | 135 |
| 4 | 25 | 30 | 150 |
Determinar una ecuación para una superficie de respuesta que proporcione un modelo adecuado para predecir el efecto del catalizador y la temperatura sobre el rendimiento de la reacción.
Solución
Al examinar los datos que vemos de las series 1 y 2 y de las series 3 y 4, que aumentar el factor A mientras se mantiene constante el factor B da como resultado un aumento en la respuesta; por lo tanto, se espera que mayores concentraciones del catalizador tengan un efecto favorable en el rendimiento de la reacción. También vemos en las series 1 y 3 y de las series 2 y 4, que aumentar el factor B mientras se mantiene constante el factor A da como resultado una disminución en la respuesta; por lo tanto, esperamos que un aumento de la temperatura tenga un efecto desfavorable en el rendimiento de la reacción. Finalmente, también vemos en las series 1 y 2 y de las corridas 3 y 4, que\(\Delta R\) es más positivo cuando el factor B está en su nivel superior; así, esperamos que haya una interacción positiva entre los factores A y B. Con cuatro experimentos, nos limitamos a un modelo que considera una intercepción, efectos de primer orden en A y B, y un término de interacción entre A y B
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \nonumber \]
Podemos elaborar valores para los coeficientes de este modelo resolviendo el siguiente conjunto de ecuaciones simultáneas:
\[\beta_0 + 15 \beta_a + 20 \beta_b + (15)(20) \beta_{ab} = \beta_0 + 15 \beta_a + 20 \beta_b + 300 \beta_{ab} = 145 \nonumber \]
\[\beta_0 + 25 \beta_a + 20 \beta_b + (25)(20) \beta_{ab} = \beta_0 + 25 \beta_a + 20 \beta_b + 500 \beta_{ab} = 158 \nonumber \]
\[\beta_0 + 15 \beta_a + 30 \beta_b + (15)(30) \beta_{ab} = \beta_0 + 15 \beta_a + 30 \beta_b + 450 \beta_{ab} = 135 \nonumber \]
\[\beta_0 + 25 \beta_a + 30 \beta_b + (25)(30) \beta_{ab} = \beta_0 + 25 \beta_a + 30 \beta_b + 750 \beta_{ab} = 150 \nonumber \]
Para resolver este conjunto de ecuaciones, restamos la primera ecuación de la segunda ecuación y restamos la tercera ecuación de la cuarta ecuación, dejándonos con las siguientes dos ecuaciones
\[10 \beta_a + 200 \beta_{ab} = 13 \nonumber \]
\[10 \beta_a + 300 \beta_{ab} = 15 \nonumber \]
A continuación, restar la primera de estas ecuaciones de la segunda da
\[100 \beta_{ab} = 2 \nonumber \]
o\(\beta_{ab} = 0.02\). Sustituir la espalda da
\[10 \beta_{a} + 200 \times 0.02 = 13 \nonumber \]
o\(\beta_a = 0.9\). Restar la ecuación para el primer experimento de la ecuación para el tercer experimento da
\[10 \beta_b + 150 \beta_{ab} = -10 \nonumber \]
Sustituyendo en 0.02\(\beta_{ab}\) y resolviendo da\(\beta_b = -1.3\). Finalmente, sustituyendo en nuestros valores por\(\beta_a\)\(\beta_b\), y\(\beta_{ab}\) en cualquiera de las cuatro primeras ecuaciones da\(\beta_0 = 151.5\). Nuestro modelo final es
\[R = 151.5 + 0.9 A - 1.3 B + 0.02 AB \nonumber\]
Cuando consideramos cómo interpretar nuestra ecuación empírica para la superficie de respuesta, debemos considerar varias limitaciones importantes:
- La intercepción en nuestro modelo representa una condición muy alejada de nuestros experimentos: En este caso, la intercepción da el rendimiento de la reacción en ausencia de catalizador y a una temperatura de 0°C, cualquiera de las cuales puede que no seamos condiciones útiles. En general, nunca es buena idea extrapolar un modelo mucho más allá de las condiciones utilizadas para definir el modelo.
- El signo de los efectos de primer orden de un factor puede ser engañoso si existe una interacción significativa entre éste y otros factores. Aunque nuestro modelo muestra que el factor B (la temperatura) tiene un efecto negativo de primer orden, la interacción positiva entre los dos factores significa que hay condiciones en las que un aumento en B aumentará el rendimiento de la reacción.
- Es difícil juzgar la importancia relativa de dos o más factores examinando sus coeficientes si sus escalas no son las mismas. Esto podría presentar un problema, por ejemplo, si reportáramos la cantidad de catalizador (factor A) usando concentraciones molares ya que estos valores serían tres órdenes de magnitud menores que las temperaturas reportadas.
- Cuando el número de variables es el mismo que el número de experimentos, como es el caso aquí, entonces no hay grados de libertad y no tenemos una manera sencilla de probar la idoneidad del modelo.
Determinar el modelo empírico usando niveles de factores codificados
Podemos abordar dos de las limitaciones descritas anteriormente mediante el uso de niveles de factores codificados en los que asignamos\(+1\) para un nivel alto y\(-1\) para un nivel bajo. Definir el límite superior y el límite inferior de los factores como\(+1\) y\(-1\) hace dos cosas para nosotros: coloca la intercepción en el centro de nuestros experimentos, lo que evita la preocupación de extrapolar nuestro modelo; y coloca todos los factores en una escala común, y lo que facilita la comparación de los efectos relativos de los factores. La codificación también facilita la determinación de la ecuación del modelo empírico cuando completamos los cálculos a mano.
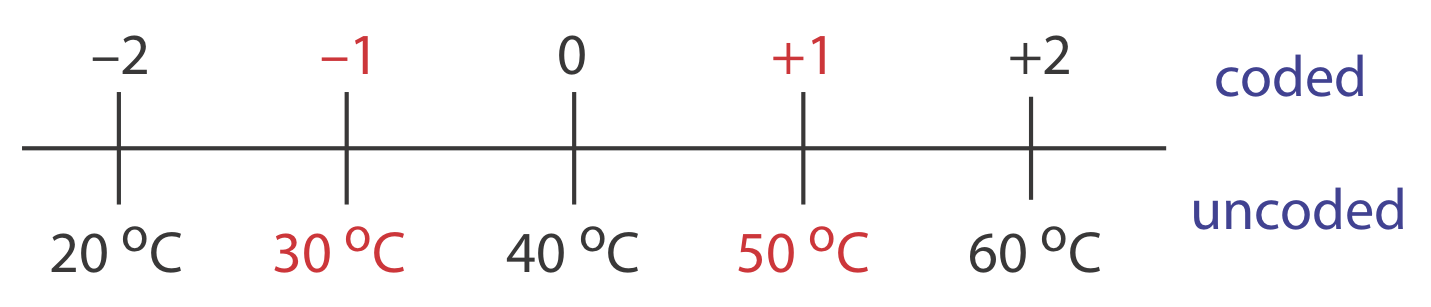
Para explorar el efecto de la temperatura en una reacción, asignamos 30 o C a un nivel de factor codificado\(-1\) y asignamos un nivel codificado\(+1\) a una temperatura de 50 o C. Qué temperatura corresponde a un nivel codificado de\(-0.5\) y cuál es el nivel codificado para una temperatura de 60 o C?
Solución
La diferencia entre\(-1\) y\(+1\) es 2, y la diferencia entre 30 o C y 50 o C es 20 o C; así, cada unidad en forma codificada es equivalente a 10 o C en forma no codificada. Con esta información, es fácil crear una escala simple entre los valores codificados y los no codificados, como se muestra en la Figura\(\PageIndex{2}\). Una temperatura de 35 o C corresponde a un nivel codificado de\(-0.5\) y un nivel codificado de\(+2\) corresponde a una temperatura de 60 o C.
Como vemos en el siguiente ejemplo, los niveles factoriales simplifican los cálculos para un modelo empírico.
Ejemplo de retrabajo\(\PageIndex{1}\) usando niveles de factores codificados.
Solución
La siguiente tabla muestra los niveles de factores originales (A y B), sus correspondientes niveles de factores codificados (A* y B*) y A*B*, que es el término de interacción del modelo empírico.
| correr | A | B | A* | B* | A*B* | R |
|---|---|---|---|---|---|---|
| 1 | 15 | 20 | \(-1\) | \(-1\) | \(+1\) | 145 |
| 2 | 25 | 20 | \(+1\) | \(-1\) | \(-1\) | 158 |
| 3 | 15 | 30 | \(-1\) | \(+1\) | \(-1\) | 135 |
| 4 | 25 | 30 | \(+1\) | \(+1\) | \(+1\) | 150 |
La ecuación empírica tiene cuatro desconocidas, los cuatro términos beta, y la Tabla\(\PageIndex{1}\) describe los cuatro experimentos. Tenemos la información suficiente para calcular los valores de\(\beta_0\),\(\beta_a\),\(\beta_b\), y\(\beta_{ab}\). Al trabajar con los niveles de factores codificados, los valores de estos parámetros son fáciles de calcular utilizando las siguientes ecuaciones, donde n es el número de corridas.
\[\beta_{0} \approx b_{0}=\frac{1}{n} \sum_{i=1}^{n} R_{i} \nonumber \]
\[\beta_{a} \approx b_{a}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} R_{i} \nonumber \]
\[\beta_{b} \approx b_{b}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} R_{i} \nonumber \]
\[\beta_{ab} \approx b_{ab}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} R_{i} \nonumber \]
Resolviendo para los parámetros estimados usando los datos de la Tabla\(\PageIndex{1}\)
\[b_{0}=\frac{145 + 158 + 135 + 150}{4} = 147 \nonumber\]
\[b_{a}=\frac{-145 + 158 - 135 + 150}{4} = 7 \nonumber\]
\[b_{b}=\frac{-145 - 11.5 + 135 + 150}{4} = 5.0 \nonumber\]
\[b_{ab}=\frac{145 - 158 - 135 + 150}{4} = 0.5 \nonumber\]
nos deja con el modelo empírico codificado para la superficie de respuesta.
\[R = 147 + 7 A^* - 4.5 B^* + 0.5 A^* B^* \nonumber \]
¿Ves por qué las ecuaciones para calcular\(b_0\),\(b_a\),\(b_b\), y\(b_{ab}\) funcionan? Tomemos\(b_a\) como ejemplo la ecuación
\[\beta_{a} \approx b_{a}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} R_{i} \nonumber \]
donde
\[b_{a}=\frac{-145 + 158 - 135 + 150}{4} = 7 \nonumber\]
El primero y el tercer términos de esta ecuación dan la respuesta cuando\(A^*\) está en su nivel bajo, y el segundo y cuarto términos en esta ecuación dan la respuesta cuando\(A^*\) está en su nivel alto. En los dos términos donde\(A^*\) está en su nivel bajo,\(B^*\) está tanto en su nivel bajo (primer término) como en su nivel alto (tercer término), y en los dos términos donde\(A^*\) está en su nivel alto,\(B^*\) está tanto en su nivel bajo (segundo término) como en su nivel alto (cuarto término). En consecuencia, la contribución de\(B^*\) se elimina del cálculo. Lo mismo es cierto para el efecto de\(A^* B^*\), aunque esto se deja para que lo confirmes.
Podemos transformar el modelo codificado en un modelo no codificado señalando eso\(A = 20 + 5A^*\) y aquello\(B = 25 + 5B^*\), resolviendo para\(A^*\) y\(B^*\), para obtener\(A^* = 0.2 A - 4\) y\(B^* = 0.2 B - 5\), y sustituyendo en el modelo codificado y simplificando.
\[R = 147 + 7 (0.2A - 4) - 4.5 (0.2B - 5) + 0.5(0.2A - 4)(0.2A - 5) \nonumber\]
\[R = 147 + 1.4A - 28 - 0.9B + 22.5 + 0.02AB - 0.5A - 0.4B + 10 \nonumber\]
\[R = 151.5 + 0.9A - 1.3B + 0.02AB \nonumber \]
Tenga en cuenta que esta es la misma ecuación que derivamos en Ejemplo\(\PageIndex{1}\) usando valores no codificados para los factores.
Aunque podemos convertir este modelo codificado a su forma no codificada, no hay necesidad de hacerlo. Si queremos conocer la respuesta para un nuevo conjunto de niveles de factores, simplemente los convertimos en forma codificada y calculamos la respuesta. Por ejemplo, si A es 23 y B es 22, entonces\(A^* = 02 \times 23 - 4 = 0.6\) y\(B^* = 0.2 \times 22 - 5 = -0.6\) y
\[R = 147 + 7 \times 0.6 - 4.5 \times (-0.6) + 0.5 \times 0.6 \times (-0.6) = 153.72 \approx 154 \text{ mg} \nonumber \]
Podemos extender este enfoque a cualquier número de factores. Para un sistema con tres factores —A, B y C — podemos utilizar un diseño factorial 2 3 para determinar los parámetros en el siguiente modelo empírico
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_c C + \beta_{ab} AB + \beta_{ac} AC + \beta_{bc} BC + \beta_{abc} ABC \nonumber \]
donde A, B y C son los niveles de factores. Los términos\(\beta_0\),\(\beta_a\),\(\beta_b\), y\(\beta_{ab}\) se estiman utilizando las siguientes ocho ecuaciones.
\[\beta_{0} \approx b_{0}=\frac{1}{n} \sum_{i=1}^{n} R_{i} \nonumber \]
\[\beta_{a} \approx b_{a}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} R_{i} \nonumber \]
\[\beta_{b} \approx b_{b}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} R_{i} \nonumber \]
\[\beta_{ab} \approx b_{ab}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} R_{i} \nonumber \]
\[\beta_{c} \approx b_{c}=\frac{1}{n} \sum_{i=1}^{n} C^*_{i} R \nonumber \]
\[\beta_{ac} \approx b_{ac}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} C^*_{i} R \nonumber \]
\[\beta_{bc} \approx b_{bc}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} C^*_{i} R \nonumber \]
\[\beta_{abc} \approx b_{abc}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} C^*_{i} R \nonumber \]
La siguiente tabla enumera los niveles de factores no codificados, los niveles de factores codificados y las respuestas para un diseño factorial 2 3.
| correr | A | B | C | A* | B* | C* | A*B* | A*C* | B*C* | A*B*C* | R |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15 | 30 | 45 | \(+1\) | \(+1\) | \(+1\) | \(+1\) |
\(+1\) |
\(+1\) |
\(+1\) |
137.5 |
| 2 | 15 | 30 | 15 | \(+1\) | \(+1\) | \(-1\) | \(+1\) | \(-1\) | \(-1\) | \(-1\) | 54.75 |
| 3 | 15 | 10 | 45 | \(+1\) | \(-1\) | \(+1\) | \(-1\) | \(+1\) | \(-1\) | \(-1\) | 73.75 |
| 4 | 15 | 10 | 15 | \(+1\) | \(-1\) | \(-1\) | \(-1\) | \(-1\) | \(+1\) | \(+1\) | 30.25 |
| 5 | 5 | 30 | 45 | \(-1\) | \(+1\) | \(+1\) | \(-1\) | \(-1\) | \(+1\) | \(-1\) | 61.75 |
| 6 | 5 | 30 | 15 | \(-1\) | \(+1\) | \(-1\) | \(-1\) | \(+1\) | \(-1\) | \(+1\) | 30.25 |
| 7 | 5 | 10 | 45 | \(-1\) | \(-1\) | \(+1\) | \(+1\) | \(-1\) | \(-1\) | \(+1\) | 41.25 |
| 8 | 5 | 10 | 15 | \(-1\) | \(-1\) | \(-1\) | \(+1\) | \(+1\) | \(+1\) | \(-1\) | 18.75 |
Determinar el modelo empírico codificado para la superficie de respuesta con base en la siguiente ecuación.
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_c C + \beta_{ab} AB + \beta_{ac} AC + \beta_{bc} BC + \beta_{abc} ABC \nonumber \]
¿Cuál es la respuesta esperada cuando A es 10, B es 15 y C es 50?
Solución
La ecuación para el modelo empírico tiene ocho desconocidas, los ocho términos beta, y la tabla anterior describe ocho experimentos. Tenemos la información suficiente para calcular valores para\(\beta_0\),\(\beta_a\),\(\beta_b\),\(\beta_{ab}\),\(\beta_{ac}\)\(\beta_{bc}\), y\(\beta_{abc}\); estos valores son
\[b_{0}=\frac{1}{8} \times(137.25+54.75+73.75+30.25+61.75+30.25+41.25+18.75 )=56.0 \nonumber\]
\[b_{a}=\frac{1}{8} \times(137.25+54.75+73.75+30.25-61.75-30.25-41.25-18.75 )=18.0 \nonumber\]
\[b_{b}=\frac{1}{8} \times(137.25+54.75-73.75-30.25+61.75+30.25-41.25-18.75 )=15.0 \nonumber\]
\[b_{c}=\frac{1}{8} \times(137.25-54.75+73.75-30.25+61.75-30.25+41.25-18.75 )=22.5 \nonumber\]
\[b_{ab}=\frac{1}{8} \times(137.25+54.75-73.75-30.25-61.75-30.25+41.25+18.75 )=7.0 \nonumber\]
\[b_{ac}=\frac{1}{8} \times(137.25-54.75+73.75-30.25-61.75+30.25-41.25+18.75 )=9.0 \nonumber\]
\[b_{bc}=\frac{1}{8} \times(137.25-54.75-73.75+30.25+61.75-30.25-41.25+18.75 )=6.0 \nonumber\]
\[b_{abc}=\frac{1}{8} \times(137.25-54.75-73.75+30.25-61.75+30.25+41.25-18.75 )=3.75 \nonumber\]
El modelo empírico codificado, por lo tanto, es
\[R = 56.0 + 18.0 A^* + 15.0 B^* + 22.5 C^* + 7.0 A^* B^* + 9.0 A^* C^* + 6.0 B^* C^* + 3.75 A^* B^* C^* \nonumber\]
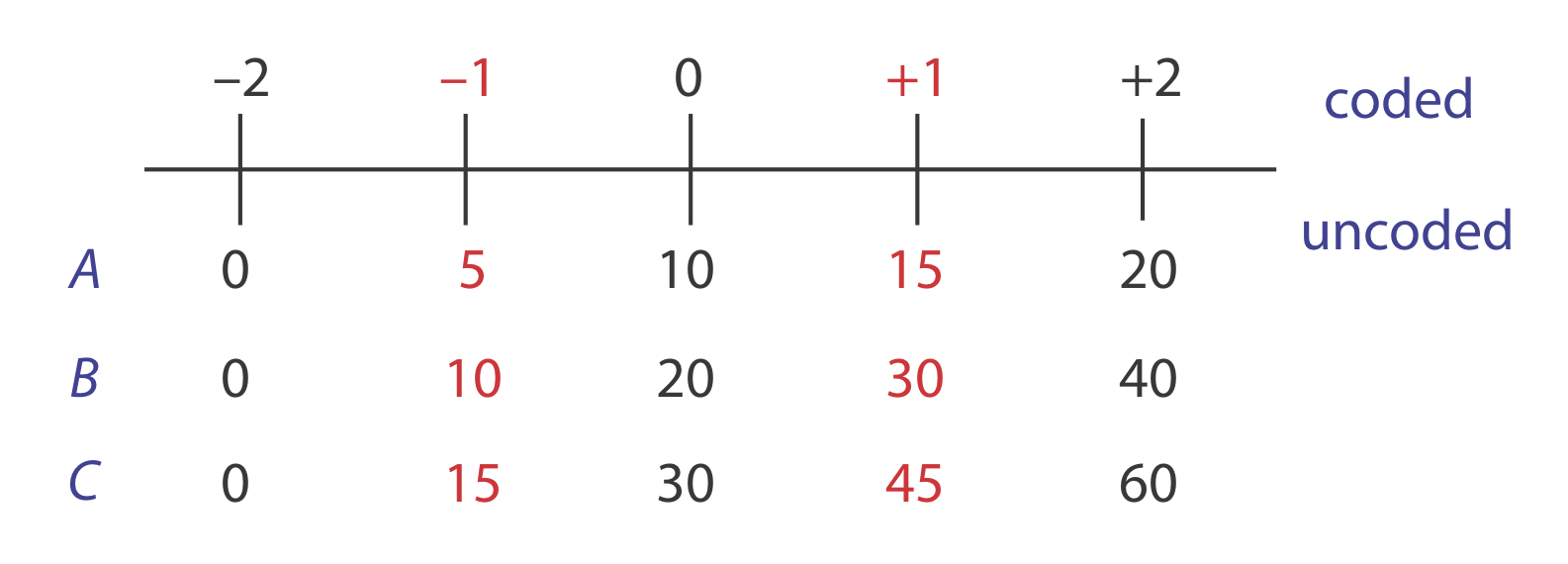
Para encontrar la respuesta cuando A es 10, B es 15 y C es 50, primero convertimos estos valores en su forma codificada. La figura nos\(\PageIndex{3}\) ayuda a realizar las conversiones adecuadas; así, A * es 0, B * es\(-0.5\) y C * es\(+1.33\). Sustituir de nuevo al modelo empírico da una respuesta de
\[R = 56.0 + 18.0 (0) + 15.0 (-0.5) + 22.5 (+1.33) + 7.0 (0) (-0.5) + 9.0 (0) (+1.33) + 6.0 (-0.5) (+1.33) + 3.75 (0) (-0.5) (+1.33) = 74.435 \approx 74.4 \nonumber\]
Evaluación de un modelo empírico
Un diseño factorial de 2 k solo puede modelar el efecto de primer orden de un factor, incluyendo interacciones de primer orden, sobre la respuesta. Un diseño factorial 2 2, por ejemplo, incluye el efecto de primer orden de cada factor (\(\beta_a\)y\(\beta_b\)) y una interacción de primer orden entre los factores (\(\beta_{ab}\)). Un diseño factorial de 2 k no puede modelar efectos de orden superior porque no hay suficiente información. Aquí hay un ejemplo sencillo que ilustra el problema. Supongamos que necesitamos modelar un sistema en el que la respuesta sea una función de un solo factor, A. La figura\(\PageIndex{4a}\) muestra el resultado de un experimento utilizando un diseño factorial de 2 1. El único modelo empírico que podemos ajustar a los datos es una línea recta.
\[R = \beta_0 + \beta_a A \nonumber\]
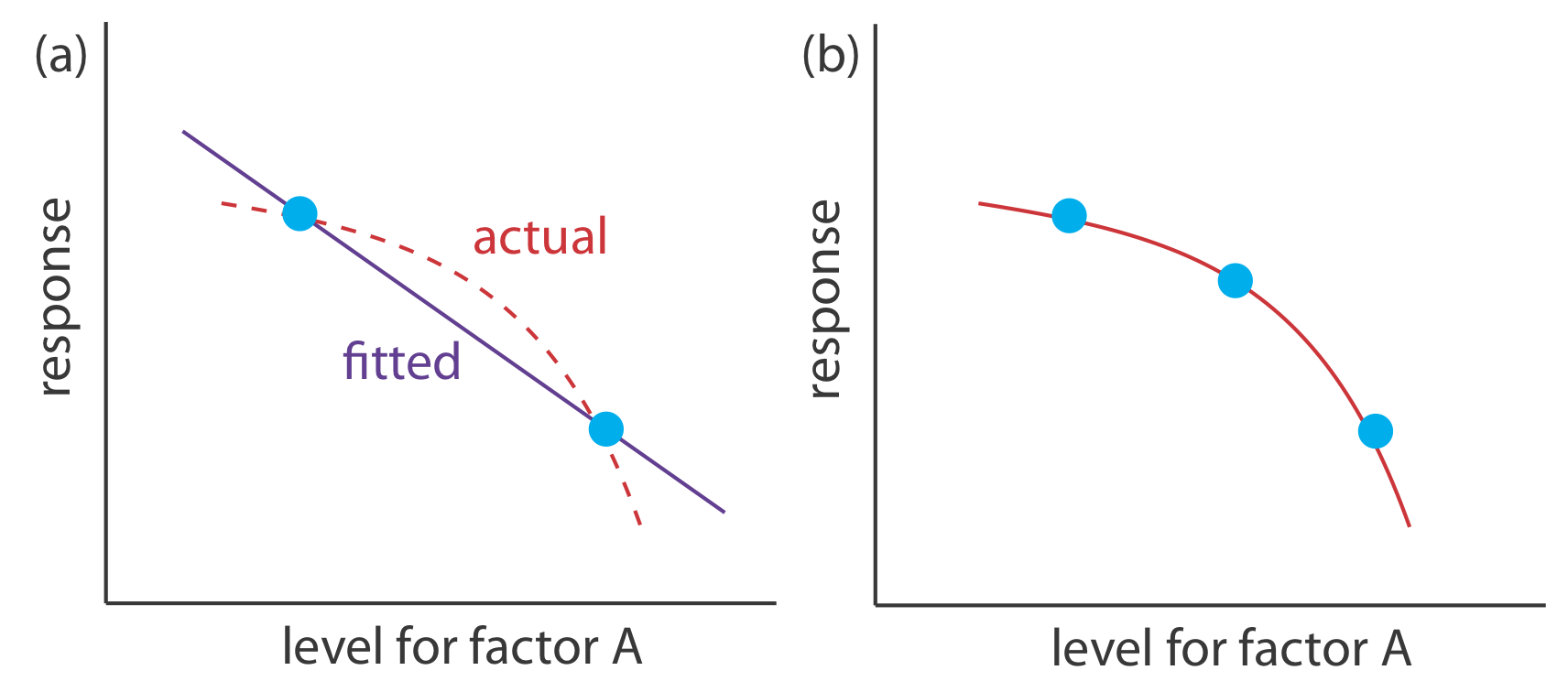
Si la respuesta real es una curva en lugar de una línea recta, entonces el modelo empírico está en error. Para ver evidencias de curvatura debemos medir la respuesta para al menos tres niveles por cada factor. Podemos ajustar el diseño factorial de 3 1 en la Figura\(\PageIndex{4b}\) a un modelo empírico que incluye efectos factoriales de segundo orden.
\[R = \beta_0 + \beta_a A + \beta_{aa} A^2 \nonumber\]
En general, un diseño factorial de nivel n puede modelar términos de factor único e interacción hasta el orden (n — 1) th.
Podemos juzgar la efectividad de un modelo empírico de primer orden midiendo la respuesta en el centro del diseño factorial. Si no hay efectos de orden superior, entonces la respuesta promedio de los ensayos en un diseño factorial de 2 k debe ser igual a la respuesta medida en el centro del diseño factorial. Para dar cuenta de la influencia de los errores aleatorios realizamos varias determinaciones de la respuesta en el centro del diseño factorial y establecemos un intervalo de confianza adecuado. Si la diferencia entre las dos respuestas es significativa, entonces un modelo empírico de primer orden probablemente sea inapropiado.
Una de las ventajas de trabajar con un modelo empírico codificado es que b 0 es la respuesta promedio de los ensayos de 2\(\times\) k en un diseño factorial de 2 k.
Un método para el análisis cuantitativo de vanadio es acidificar la solución añadiendo H 2 SO 4 y oxidando el vanadio con H 2 O 2 para formar un compuesto soluble rojizo marrón con la fórmula general (VO) 2 (SO 4) 3. Palasota y Deming estudiaron el efecto de las cantidades relativas de H 2 SO 4 y H 2 O 2 sobre la absorbancia de la solución, reportando los siguientes resultados para un diseño factorial 2 2 [Palasota, J. A.; Deming, S. N. J. Chem. Educ. 1992, 62, 560—563].
| H 2 SO 4 | H 2 O 2 | absorbancia |
|---|---|---|
| \(+1\) | \(+1\) | 0.330 |
| \(+1\) | \(-1\) | 0.359 |
| \(-1\) | \(+1\) | 0.293 |
| \(-1\) | \(-1\) | 0.420 |
Cuatro mediciones replicadas en el centro del diseño factorial dan absorbancias de 0.334, 0.336, 0.346 y 0.323. Determinar si un modelo empírico de primer orden es apropiado para este sistema. Utilice un intervalo de confianza del 90% cuando se tenga en cuenta el efecto del error aleatorio.
Solución
Comenzamos determinando el intervalo de confianza para la respuesta en el centro del diseño factorial. La respuesta media es de 0.335 con una desviación estándar de 0.0094, lo que da un intervalo de confianza del 90% de
\[\mu=\overline{X} \pm \frac{t s}{\sqrt{n}}=0.335 \pm \frac{(2.35)(0.0094)}{\sqrt{4}}=0.335 \pm 0.011 \nonumber\]
La respuesta promedio,\(\overline{R}\), desde el diseño factorial es
\[\overline{R}=\frac{0.330+0.359+0.293+0.420}{4}=0.350 \nonumber\]
Debido a que\(\overline{R}\) excede el límite superior del intervalo de confianza de 0.346, podemos suponer razonablemente que un diseño factorial de 2 2 y un modelo empírico de primer orden son inapropiados para este sistema en el nivel de confianza del 95%.
Diseños centrales de compuestos
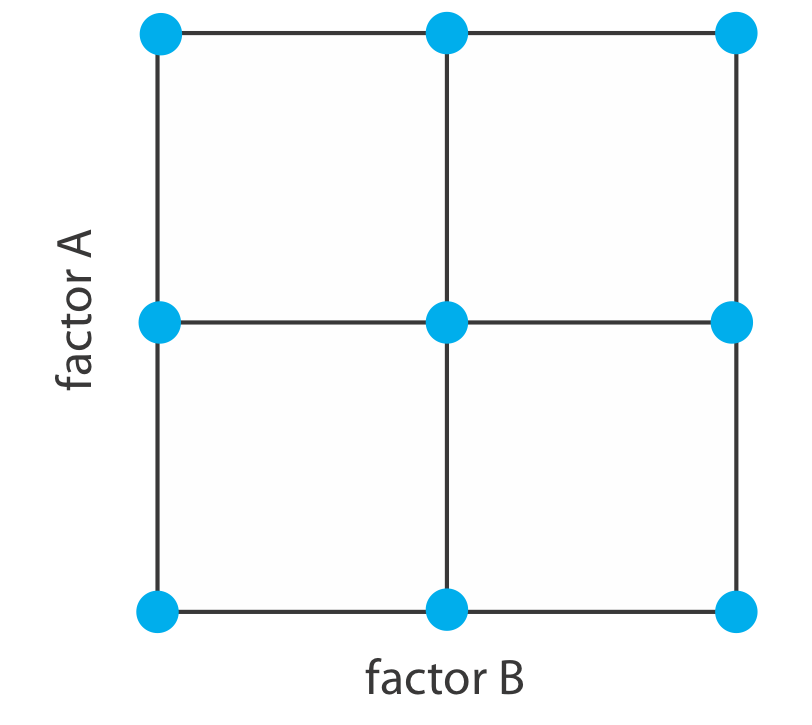
Una limitación a un diseño factorial de 3 k, que nos permitiría utilizar un modelo empírico con efectos de segundo orden, es el número de ensayos que necesitamos ejecutar. Como se muestra en la Figura\(\PageIndex{5}\), un diseño factorial 3 2 requiere 9 ensayos. Este número aumenta a 27 para tres factores y a 81 para 4 factores.
Un diseño experimental más eficiente para un sistema que contiene más de dos factores es un diseño compuesto central, dos ejemplos del cual se muestran en la Figura\(\PageIndex{6}\). El diseño compuesto central consiste en un diseño factorial de 2 k, que proporciona datos para estimar el efecto de primer orden de cada factor y las interacciones entre los factores, y un diseño de estrella que tiene\(2^k + 1\) puntos, lo que proporciona datos para estimar efectos de segundo orden. Si bien un diseño compuesto central para dos factores requiere el mismo número de ensayos, nueve, como un diseño factorial 3 2, solo requiere 15 ensayos y 25 ensayos cuando se utilizan tres factores o cuatro factores. Consulte los recursos adicionales de este capítulo para obtener detalles sobre los diseños centrales de compuestos.