Inicio
Química
Química Analítica
Quimiometría usando R (Harvey)
9: Optimización de datos
9.6: Uso de R para modelar una superficie de respuesta (regresión múltiple)

9.6: Uso de R para modelar una superficie de respuesta (regresión múltiple)

Última actualización
Guardar como PDF

Page ID: 69272

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los cálculos para determinar un modelo empírico de una superficie de respuesta utilizando un diseño factorial de 2 ^k, como se describe en la Sección 9.5, son relativamente fáciles de completar para un pequeño número de factores y para diseños experimentales sin replicación donde el número de experimentos es igual a el número de parámetros en el modelo. Si queremos trabajar con más factores, si queremos explorar otros diseños experimentales, y si queremos construir la replicación en el diseño experimental para poder evaluar mejor nuestro modelo empírico, entonces necesitamos hacerlo construyendo un modelo de regresión, como hicimos anteriormente en el Capítulo 8.

Creación de modelos empíricos usando R

Para ilustrar cómo podemos usar R para crear un modelo empírico, usemos datos de un experimento que explora cómo optimizar una reacción de Grignard que conduzca a la síntesis de bencil-1-ciclopentan-1-ol [Bouzidi, N.; Gozzi, C. J. Chem. Educ. 2008, 85, 1544—1547]. En este estudio, los estudiantes comienzan por estudiar el efecto de seis posibles factores sobre el rendimiento de la reacción: el volumen de éter dietílico utilizado para preparar una solución de cloruro de bencilo$x_1$, el tiempo durante el cual se agrega cloruro de bencilo a la mezcla de reacción$x_2$, el tiempo de agitación utilizado para preparar el cloruro de bencil-magnesio$x_3$,, el exceso relativo de cloruro de bencilo a ciclopentanona$x_4$, el exceso relativo de viruta de magnesio a cloruro de bencilo$x_5$, y el tiempo de reacción,$x_6$.

Con seis factores a considerar, un diseño factorial completo de 2 ^k requiere 32 experimentos, lo que requiere mucha mano de obra. En cambio, los estudiantes comienzan con un estudio de tamizaje que utiliza ocho experimentos para modelar solo los efectos de primer orden de los seis factores, como se describe en las siguientes dos tablas.

Tabla$\PageIndex{1}$: Niveles de factores para estudio de tamizaje
factor	bajo nivel	levcel alto
$x_1$: volumen de éter dietílico en mL	18	50
$x_2$: tiempo de adición en min	60	90
$x_3$: tiempo de agitación en min	20	40
$x_4$: exceso relativo de cloruro de bencilo como%	20	30
$x_5$: exceso relativo de magnesio como%	12.5	25
$x_6$: tiempo de reacción en min	30	60

Tabla$\PageIndex{2}$: Diseño experimental que muestra niveles de factores codificados y respuestas
correr	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	porcentaje de rendimiento
1	\ (x_1\) ">$+1$	\ (x_2\) ">$+1$	\ (x_3\) ">$+1$	\ (x_4\) ">$-1$	\ (x_5\) ">$+1$	\ (x_6\) ">$-1$	72
2	\ (x_1\) ">$-1$	\ (x_2\) ">$+1$	\ (x_3\) ">$+1$	\ (x_4\) ">$+1$	\ (x_5\) ">$-1$	\ (x_6\) ">$+1$	33
3	\ (x_1\) ">$-1$	\ (x_2\) ">$-1$	\ (x_3\) ">$+1$	\ (x_4\) ">$+1$	\ (x_5\) ">$+1$	\ (x_6\) ">$-1$	29
4	\ (x_1\) ">$+1$	\ (x_2\) ">$-1$	\ (x_3\) ">$-1$	\ (x_4\) ">$+1$	\ (x_5\) ">$+1$	\ (x_6\) ">$+1$	74
5	\ (x_1\) ">$-1$	\ (x_2\) ">$+1$	\ (x_3\) ">$-1$	\ (x_4\) ">$-1$	\ (x_5\) ">$+1$	\ (x_6\) ">$+1$	31
6	\ (x_1\) ">$+1$	\ (x_2\) ">$+1$	\ (x_3\) ">$+1$	\ (x_4\) ">$-1$	\ (x_5\) ">$-1$	\ (x_6\) ">$+1$	52
7	\ (x_1\) ">$+1$	\ (x_2\) ">$-1$	\ (x_3\) ">$-1$	\ (x_4\) ">$+1$	\ (x_5\) ">$-1$	\ (x_6\) ">$-1$	47
8	\ (x_1\) ">$-1$	\ (x_2\) ">$-1$	\ (x_3\) ">$-1$	\ (x_4\) ">$-1$	\ (x_5\) ">$-1$	\ (x_6\) ">$-1$	27

Para realizar los cálculos en R primero creamos vectores para los niveles de factores codificados y las respuestas.

x1 = c (1, -1, -1,1, -1,1,1, -1) x2 = c (1,1, -1, -1,1, -1) x3 = c (1,1,1, -1, -1,1, -1, -1) x4 = c (-1,1,1,1, -1, -1, -1,1, -1) x5 = c (1, -1,1,1,1, -1, -1, -1) x6 = c (-1,1, -1,1,1, -1, -1) rendimiento = c (72,33,29,74,31,52,47,27)

A continuación, usamos la función lm () para construir un modelo de regresión lineal que incluya solo los efectos de primer orden de los factores (consulte el Capítulo 8.5 para revisar la sintaxis de esta función), y la función summary () para revisar el modelo resultante.

tamizado = lm (rendimiento ~ x1 + x2 + x3 + x4 + x5 + x6) resumen (cribado)

Llamar a:

lm (fórmula = rendimiento ~ x1 + x2 + x3 + x4 + x5 + x6)

Residuales:

1 2 3 4 5 6 7 8

5.875 5.875 -5.875 5.875 -5.875 -5.875 -5.875 5.875 5.875

Coeficientes:

Estimar Std.Error t valor Pr (>|t|)

(Intercepción) 45.625 5.875 7.766 0.0815.

x1 15.625 5.875 2.660 0.2290

x2 0.125 5.875 0.021 0.9865

x3 0.875 5.875 0.149 0.9059

x4 0.125 5.875 0.021 0.9865

x5 5.875 5.875 1.000 0.5000

x6 1.875 5.875 0.319 0.8033

—

Signif. códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1

Error estándar residual: 16.62 en 1 grados de libertad

R al cuadrado múltiple: 0.8913, R cuadrado ajustado: 0.239

Estadístico F: 1.366 sobre 6 y 1 DF, valor p: 0.5749

Debido a que tenemos un experimento más que variables en nuestro modelo empírico, el resumen proporciona cierta información sobre la importancia de los parámetros del modelo; sin embargo, con solo un grado de libertad esta información no es realmente confiable. Además de la intercepción, los tres factores con mayores coeficientes son el volumen de éter dietílico$x_1$, el exceso relativo de magnesio$x_5$, y el tiempo de reacción,$x_6$.

Habiendo identificado tres factores para una mayor investigación, los estudiantes utilizan un diseño factorial 2 ³ para explorar las interacciones entre estos tres factores utilizando el diseño experimental en la siguiente tabla (ver Tabla$\PageIndex{1}$ para los niveles de factores reales.

Tabla$\PageIndex{3}$: Niveles de factores codificados y respuesta para un diseño$2^3$ factorial
correr	$x_1$	$x_5$	$x_6$	porcentaje de rendimiento
1	\ (x_1\)” class="lt-chem-290715">$-1$	\ (x_5\)” class="lt-chem-290715">$-1$	\ (x_6\)” class="lt-chem-290715">$-1$	28.5
2	\ (x_1\)” class="lt-chem-290715">$+1$	\ (x_5\)” class="lt-chem-290715">$-1$	\ (x_6\)” class="lt-chem-290715">$-1$	55.5
3	\ (x_1\)” class="lt-chem-290715">$-1$	\ (x_5\)” class="lt-chem-290715">$+1$	\ (x_6\)” class="lt-chem-290715">$-1$	38
4	\ (x_1\)” class="lt-chem-290715">$+1$	\ (x_5\)” class="lt-chem-290715">$+1$	\ (x_6\)” class="lt-chem-290715">$-1$	68
5	\ (x_1\)” class="lt-chem-290715">$-1$	\ (x_5\)” class="lt-chem-290715">$-1$	\ (x_6\)” class="lt-chem-290715">$+1$	49
6	\ (x_1\)” class="lt-chem-290715">$+1$	\ (x_5\)” class="lt-chem-290715">$-1$	\ (x_6\)” class="lt-chem-290715">$+1$	66
7	\ (x_1\)” class="lt-chem-290715">$-1$	\ (x_5\)” class="lt-chem-290715">$+1$	\ (x_6\)” class="lt-chem-290715">$+1$	31.5
8	\ (x_1\)” class="lt-chem-290715">$+1$	\ (x_5\)” class="lt-chem-290715">$+1$	\ (x_6\)” class="lt-chem-290715">$+1$	72

Como antes, creamos vectores para nuestros factores y la respuesta y luego usamos las funciones lm () y summary () para completar y evaluar el modelo empírico resultante.

x1 = c (-1,1, -1,1, -1,1, -1,1) x5 = c (-1, -1,1,1, -1, -1,1,1) x6 = c (-1, -1, -1, -1, 1,1,1,1) rendimiento = c (28.5,55.5,38,68,49,66,31.5,72) hecho23 = lm (rendimiento ~ x1 * x5 * x6) resumen (hecho23)

Llamar a:

lm (fórmula = rendimiento ~ x1 * x5 * x6)

Residuales:

TODOS los 8 residuos son 0: ¡no hay grados residuales de libertad!

Coeficientes:

Estimación Std. Error t valor Pr (>|t|)

(Intercepción) 51.0625 NA NA NA

x1 14.3125 NA NA NA

x5 1.3125 NA NA NA

x6 3.5625 NA NA NA

x1:x5 3.3125 NA NA NA

x1:x6 0.0625 NA NA NA

x5:x6 -4.1875 NA NA NA

x1:x5:x6 2.5625 NA NA NA

Error estándar residual: NaN en 0 grados de libertad

R al cuadrado múltiple: 1, R cuadrado ajustado: NaN

Estadístico F: NaN en 7 y 0 DF, valor p: NA

Con ocho experimentos y ocho variables en el modelo empírico, no tenemos ninguna capacidad para evaluar estadísticamente el modelo. De los tres efectos de primer orden, vemos que el volumen de éter dietílico,$x_1$, y el tiempo de reacción$x_6$,, son más importantes que el exceso relativo de magnesio,$x_5$. También vemos que la interacción entre$x_1$ y$x_5$ es positiva (valores altos para ambos favorecen un aumento del rendimiento) y que la interacción entre$x_5$ y$x_6$ es negativa (los rendimientos mejoran cuando un factor es alto y el otro es bajo).

Finalmente, los estudiantes utilizan un modelo compuesto central, que permite agregar efectos de segundo orden y curvatura en la superficie de respuesta, para estudiar el efecto del volumen de éter dietílico$x_1$, y el tiempo de reacción$x_6$, sobre el rendimiento porcentual. El exceso relativo de magnesio,$x_5$ se fijó en su nivel alto para este estudio debido a que esto proporciona mayores rendimientos porcentuales (comparar los resultados para las series 4 y 6 con los resultados para las series 3 y 5 en la Tabla$\PageIndex{3}$). En las siguientes tablas se proporciona el diseño experimental.

Tabla$\PageIndex{4}$: Niveles de factores codificados y respuestas para un diseño experimental compuesto central
correr	$x_1$	$x_6$	porcentaje de rendimiento
1	\ (x_1\) ">$-1$	\ (x_6\) ">$-1$	39
2	\ (x_1\) ">$+1$	\ (x_6\) ">$-1$	66.5
3	\ (x_1\) ">$-1$	\ (x_6\) ">$+1$	22
4	\ (x_1\) ">$+1$	\ (x_6\) ">$+1$	72.5
5	\ (x_1\) ">$-1.414$	\ (x_6\) ">0	10.5
6	\ (x_1\) ">$+1.414$	\ (x_6\) ">0	72.5
7	\ (x_1\) ">0	\ (x_6\) ">$-1.414$	38
8	\ (x_1\) ">0	\ (x_6\) ">$+1.414$	70
9	\ (x_1\) ">0	\ (x_6\) ">0	59
10	\ (x_1\) ">0	\ (x_6\) ">0	57
11	\ (x_1\) ">0	\ (x_6\) ">0	54.5
12	\ (x_1\) ">0	\ (x_6\) ">0	63

Como antes, creamos vectores para nuestros factores y la respuesta, y luego usamos las funciones lm () y summary () para completar y evaluar el modelo empírico resultante.

x1 = c (-1,1, -1,1, -1.414,1.414,0,0,0,0,0,0) x6 = c (-1, -1,1,1,0,0, -1.414,1.414,0,0,0,0) rendimiento = c (39,66.5,22,72.5,10.5,72.5,72.5,72.5,72.5,72.5,72.5,72.5,70,70,59,57,54.5,63) centcomp = lm (rendimiento ~ x1 * x6 + I (x1^2) + I (x6^2)) resumen (centcomp)

Llamar a:

lm (fórmula = rendimiento ~ x1 * x6 + I (x1^2) + I (x6^2))

Residuales:

Mín 1Q Mediana 3Q Máx

-11.0724 -4.0794 -0.3938 5.2056 9.3695

Coeficientes:

Estimación Std. Error t valor Pr (>|t|)

(Intercepción) 58.375 4.360 13.389 1.07e-05 ***

x1 20.712 3.083 6.718 0.000529 ***

x6 4.282 3.083 1.389 0.214267

I (x1^2) -7.876 3.447 -2.285 0.062398.

I (x6^2) -1.625 3.447 -0.471 0.654130

x1:x6 5.750 4.360 1.319 0.235317

—

Signif. códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1

Error estándar residual: 8.72 en 6 grados de libertad

R al cuadrado múltiple: 0.9, R cuadrado ajustado: 0.8167

Estadístico F: 10.8 sobre 5 y 6 DF, valor p: 0.005835

Con 12 experimentos y solo seis variables, nuestro modelo tiene suficientes grados de libertad para sugerir que proporciona una imagen razonable de cómo el tiempo de reacción y el volumen de éter dietílico afectan el rendimiento de la reacción incluso si los errores residuales en las respuestas van desde un mínimo de -11.7 a un máximo +9. 37. El 50% medio de los errores residuales oscilan entre -4.1 y +5.2 con una mediana de error residual de -0.4. Podemos comparar los rendimientos experimentales reales con los rendimientos predichos por el modelo combinándolos en un marco de datos.

centcomp_results = data.frame (yield, centcomp$fitted.values, yield - centcomp$fitted.values) colnames (centcomp_results) = c (“rendimiento expt”, “rendimiento pred”, “error residual”) centcomp_results

rendimiento expt rendimiento pred error residual

1 39.0 29.63046 9.3695385

2 66.5 59.55372 6.9462836

3 22.0 26.69375 -4.6937546

4 72.5 79.61701 -7.1170095

5 10.5 13.34036 -2.8403635

6 72.5 71.91285 0.5871540

7 38.0 49.07236 -11.0723566

8 70.0 61.18085 8.8191471

9 59.0 58.37466 0.6253402

10 57.0 58.37466 -1.3746598

11 54.5 58.37466 -3.8746598

12 63.0 58.37466 4.6253402

Uso de R para visualizar la superficie de respuesta

El paquete Plot3D proporciona varias funciones que podemos usar para visualizar una superficie de respuesta definida por dos factores. Aquí consideramos tres funciones, una para dibujar una gráfica de contorno bidimensional de la superficie de respuesta, otra para dibujar una gráfica de superficie tridimensional de la respuesta y otra para trazar una gráfica de dispersión tridimensional de las respuestas. Para comenzar, usamos la función library () para que el paquete esté disponible para nosotros (nota: es posible que primero deba instalar el paquete Plot3D; consulte el Capítulo 1 para obtener detalles sobre cómo hacerlo).

biblioteca (Plot3D)

Comencemos por crear una gráfica de contorno bidimensional de nuestra superficie de respuesta que coloque el volumen de éter dietílico$x_1$, en el eje x y el tiempo de reacción,$x_6$ en el eje y, y utilizando respuestas calculadas del modelo para dibujar las curvas de nivel. Primero, creamos vectores con valores para el eje x y el eje y

x1_eje = seq (-1.5, 1.5, 0.1) x6_eje = seq (-1.5 ,1.5, 0.1)

A continuación, creamos una función que utiliza nuestro modelo empírico para calcular la respuesta para cada combinación de x1_axis y x6_axis

response = función (x, y) {coef (centcomp) [1] + coef (centcomp) [2] *x + coef (centcomp) [3] *y + coef (centcomp) [4] *x^2 + coef (centcomp) [5] *y^2 + coef (centcomp) [6] *x*y}

donde coef (centcomp) [i] se utiliza para extraer el coeficiente ^i-ésimo de nuestro modelo empírico. Ahora usamos la función outer () de R para calcular la respuesta para cada combinación de las variables x1_axis y x6_axis

z_axis = exterior (X = x1_eje, Y = x6_eje, respuesta)

Finalmente, utilizamos la función Contour2D () para crear la gráfica de contorno en la Figura$\PageIndex{1}$.

Contour2D (x = x1_axis, y = x6_axis, z = z_axis, xlab = “x1: volumen”, ylab = “x6: tiempo”, clab = “rendimiento”)

Figura$\PageIndex{1}$: Gráfica de contorno para la superficie de respuesta que predice el rendimiento porcentual en una reacción de Grignard en función del volumen de éter dietílico y el tiempo de reacción. Los valores del eje x y del eje y son niveles de factores codificados.

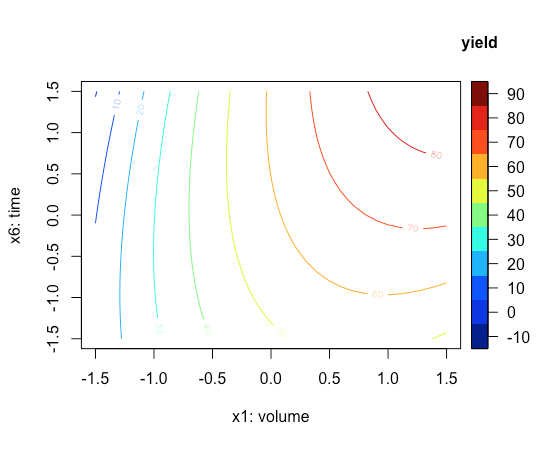
A continuación, vamos a crear una gráfica de superficie tridimensional de nuestra superficie de respuesta que coloque el volumen de éter dietílico$x_1$, en el eje x, el tiempo de reacción,$x_6$ en el eje y, y las respuestas calculadas del modelo en el eje z. Para ello, utilizamos la función Persp3D ()

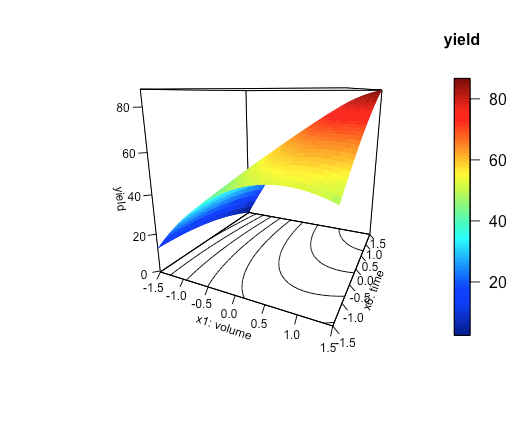
Persp3D (x = x1_axis, y = x6_axis, z = z_axis, ticktype = “detallado”, phi = 15, theta = 25, xlab = “x1: volumen”, ylab = “x6: tiempo”, zlab = “rendimiento”, clab = “rendimiento”, contorno = VERDADERO, cex.axis = 0.75, cex.lab = 0.75)

donde phi y theta ajustan el ángulo en el que vemos la superficie de respuesta, tendrás que jugar con estos valores para crear una gráfica que sea agradable de ver, y ticktype controla cuánta información se muestra en los ejes. Los comandos cex.axis y cex.lab ajustan el tamaño del texto que se muestra en los ejes, y countour = TRUE coloca una gráfica de contorno en la parte inferior de la figura. En la figura se$\PageIndex{2}$ muestra el resultado.

Figura$\PageIndex{2}$: Gráfica tridimensional de superficie (perspectiva) para la superficie de respuesta que predice el porcentaje de rendimiento en una reacción de Grignard en función del volumen de éter dietílico y el tiempo de reacción. Los valores del eje x y del eje y son niveles de factores codificados.

Finalmente, usemos la opción type = “h” para superponer una gráfica de dispersión de los datos utilizados para construir el modelo empírico sobre la gráfica de superficie tridimensional.

Dispersión3D (x = x1, y = x6, z = rendimiento, sumar = VERDADERO, tipo = “h”, pch = 19, col = “negro”, lwd = 2, colkey = FALSO)

Figura$\PageIndex{3}$: Gráfica tridimensional de superficie (perspectiva) para la superficie de respuesta que predice el porcentaje de rendimiento en una reacción de Grignard en función del volumen de éter dietílico y el tiempo de reacción mostrando los datos originales utilizados para construir el modelo empírico. Los valores del eje x y del eje y son niveles de factores codificados.

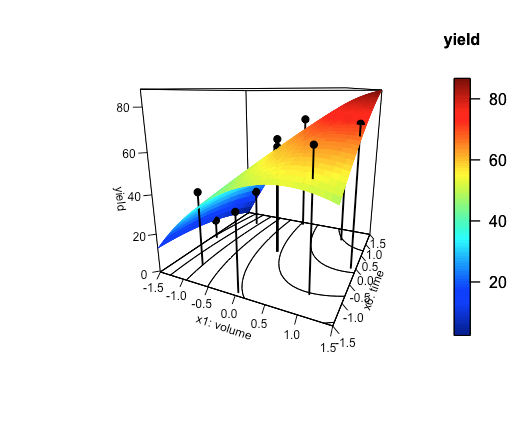
La figura$\PageIndex{3}$ muestra el resultado utilizando los datos de la Tabla$\PageIndex{4}$. Aunque la forma general de la superficie de respuesta es consistente con los datos subyacentes, existe suficiente incertidumbre experimental en los resultados de los cuatro experimentos replicados utilizados para crear este modelo empírico, como lo demuestra la desviación estándar para las series 9—12, para explicar por qué algunos de los predichos los rendimientos tienen grandes errores.

sd (rendimiento [9:12])

[1] 3.591077

correr	\(x_1\)	\(x_2\)	\(x_3\)	\(x_4\)	\(x_5\)	\(x_6\)	porcentaje de rendimiento
1	\ (x_1\) ">\(+1\)	\ (x_2\) ">\(+1\)	\ (x_3\) ">\(+1\)	\ (x_4\) ">\(-1\)	\ (x_5\) ">\(+1\)	\ (x_6\) ">\(-1\)	72
2	\ (x_1\) ">\(-1\)	\ (x_2\) ">\(+1\)	\ (x_3\) ">\(+1\)	\ (x_4\) ">\(+1\)	\ (x_5\) ">\(-1\)	\ (x_6\) ">\(+1\)	33
3	\ (x_1\) ">\(-1\)	\ (x_2\) ">\(-1\)	\ (x_3\) ">\(+1\)	\ (x_4\) ">\(+1\)	\ (x_5\) ">\(+1\)	\ (x_6\) ">\(-1\)	29
4	\ (x_1\) ">\(+1\)	\ (x_2\) ">\(-1\)	\ (x_3\) ">\(-1\)	\ (x_4\) ">\(+1\)	\ (x_5\) ">\(+1\)	\ (x_6\) ">\(+1\)	74
5	\ (x_1\) ">\(-1\)	\ (x_2\) ">\(+1\)	\ (x_3\) ">\(-1\)	\ (x_4\) ">\(-1\)	\ (x_5\) ">\(+1\)	\ (x_6\) ">\(+1\)	31
6	\ (x_1\) ">\(+1\)	\ (x_2\) ">\(+1\)	\ (x_3\) ">\(+1\)	\ (x_4\) ">\(-1\)	\ (x_5\) ">\(-1\)	\ (x_6\) ">\(+1\)	52
7	\ (x_1\) ">\(+1\)	\ (x_2\) ">\(-1\)	\ (x_3\) ">\(-1\)	\ (x_4\) ">\(+1\)	\ (x_5\) ">\(-1\)	\ (x_6\) ">\(-1\)	47
8	\ (x_1\) ">\(-1\)	\ (x_2\) ">\(-1\)	\ (x_3\) ">\(-1\)	\ (x_4\) ">\(-1\)	\ (x_5\) ">\(-1\)	\ (x_6\) ">\(-1\)	27

correr	\(x_1\)	\(x_5\)	\(x_6\)	porcentaje de rendimiento
1	\ (x_1\)” class="lt-chem-290715">\(-1\)	\ (x_5\)” class="lt-chem-290715">\(-1\)	\ (x_6\)” class="lt-chem-290715">\(-1\)	28.5
2	\ (x_1\)” class="lt-chem-290715">\(+1\)	\ (x_5\)” class="lt-chem-290715">\(-1\)	\ (x_6\)” class="lt-chem-290715">\(-1\)	55.5
3	\ (x_1\)” class="lt-chem-290715">\(-1\)	\ (x_5\)” class="lt-chem-290715">\(+1\)	\ (x_6\)” class="lt-chem-290715">\(-1\)	38
4	\ (x_1\)” class="lt-chem-290715">\(+1\)	\ (x_5\)” class="lt-chem-290715">\(+1\)	\ (x_6\)” class="lt-chem-290715">\(-1\)	68
5	\ (x_1\)” class="lt-chem-290715">\(-1\)	\ (x_5\)” class="lt-chem-290715">\(-1\)	\ (x_6\)” class="lt-chem-290715">\(+1\)	49
6	\ (x_1\)” class="lt-chem-290715">\(+1\)	\ (x_5\)” class="lt-chem-290715">\(-1\)	\ (x_6\)” class="lt-chem-290715">\(+1\)	66
7	\ (x_1\)” class="lt-chem-290715">\(-1\)	\ (x_5\)” class="lt-chem-290715">\(+1\)	\ (x_6\)” class="lt-chem-290715">\(+1\)	31.5
8	\ (x_1\)” class="lt-chem-290715">\(+1\)	\ (x_5\)” class="lt-chem-290715">\(+1\)	\ (x_6\)” class="lt-chem-290715">\(+1\)	72

factor	bajo nivel	levcel alto
\(x_1\): volumen de éter dietílico en mL	18	50
\(x_2\): tiempo de adición en min	60	90
\(x_3\): tiempo de agitación en min	20	40
\(x_4\): exceso relativo de cloruro de bencilo como%	20	30
\(x_5\): exceso relativo de magnesio como%	12.5	25
\(x_6\): tiempo de reacción en min	30	60