10.2: Mejora de la relación señal/ruido

Última actualización

30 oct 2022
Guardar como PDF
- 10.2: Mejora de la relación señal
- 10.3: Eliminación de antecedentes

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

En esta sección consideraremos tres herramientas computacionales comunes para mejorar la relación señal/ruido: promedio de señal, suavizado digital y filtrado de Fourier.

Promedio de señal

La diferencia más importante entre la señal y el ruido es que una señal es determinada (fija en valor) y el ruido es indeterminado (aleatorio en valor). Si medimos una señal pura varias veces, esperamos que su valor sea el mismo cada vez; así, si sumamos n escaneos, esperamos que la señal neta, $S_n$ , se defina como

$S_n = n S \nonumber$

donde $S$ está la señal para un solo escaneo. Debido a que el ruido es aleatorio, su valor varía de una ejecución a otra, a veces con un valor que es mayor y a veces con un valor que es menor, y a veces con un valor que es positivo y a veces con un valor que es negativo. En promedio, la desviación estándar del ruido aumenta a medida que hacemos más escaneos, pero lo hace a un ritmo más lento que para la señal

$s_n = \sqrt{n} s \nonumber$

donde $s$ es la desviación estándar para una sola exploración y $s_n$ es la desviación estándar después de n escaneos. Combinando estas dos ecuaciones, nos muestra que la relación señal/ruido $S/N$ , después de n escaneos aumenta a medida que

$(S/N)_n = \frac{S_n}{s_n} = \frac{nS}{\sqrt{n}s} = \sqrt{n}(S/N)_{n = 1} \nonumber$

donde $(S/N)_{n = 1}$ es la relación señal/ruido para el escaneo inicial. Así, cuando $n = 4$ la relación señal/ruido mejora en un factor de 2, y cuando $n = 16$ la relación señal/ruido aumenta en un factor de 4. La figura $\PageIndex{1}$ muestra la mejora en la relación señal/ruido para 1, 2, 4 y 8 exploraciones.

Figura $\PageIndex{1}$ : Mejora en la relación señal/ruido a través del promedio de señal usando 1, 2, 4 y 8 barridos. Cada gráfica muestra la señal ruidosa en azul con la señal pura superpuesta en negro. La señal total se divide por el número de escaneos para que cada *eje y* tenga la misma escala.

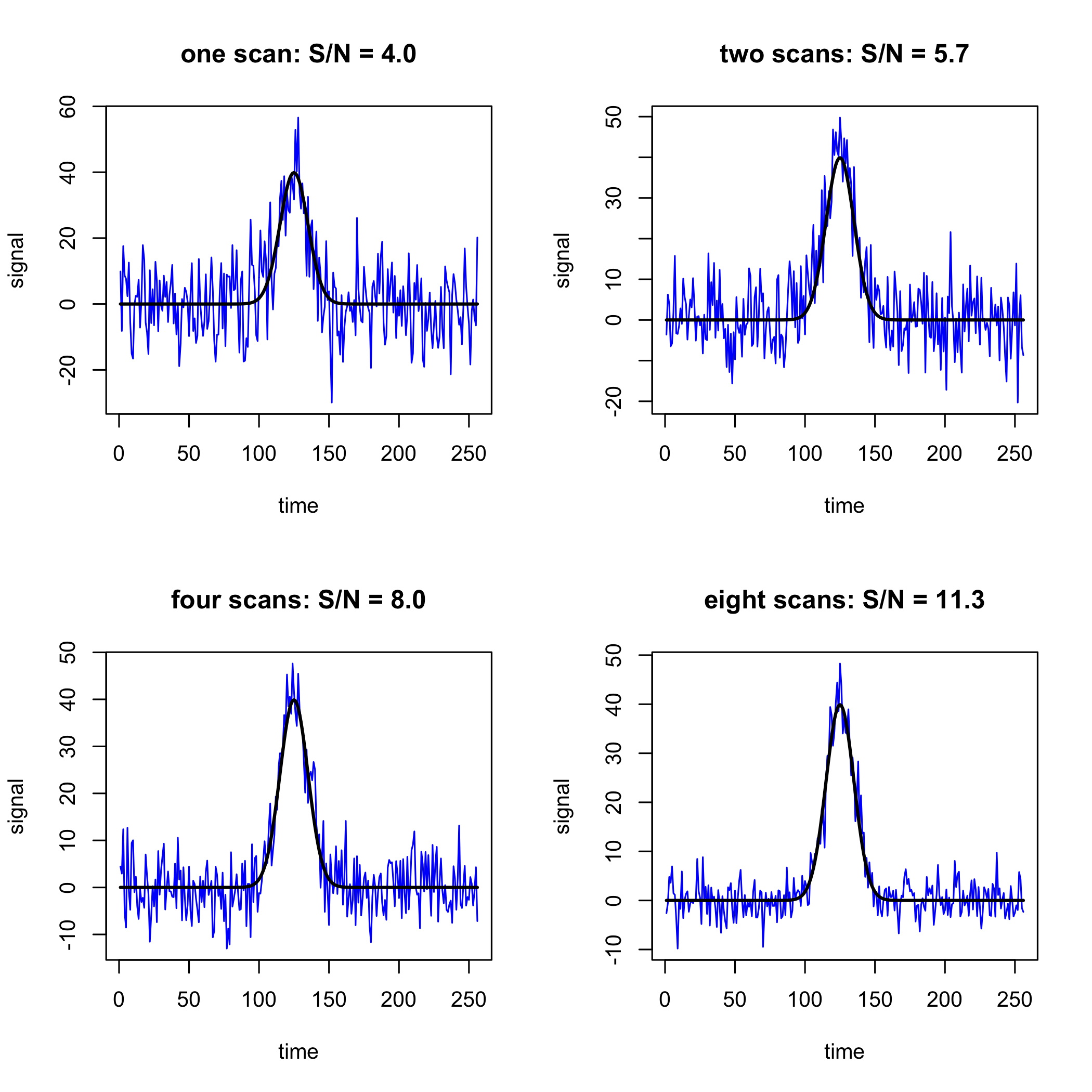
El promedio de señal funciona bien cuando el tiempo que se tarda en recolectar un solo escaneo es corto y cuando la señal del analito es estable con respecto al tiempo tanto porque la muestra es estable como el instrumento es estable; cuando este no es el caso, entonces corremos el riesgo de un cambio dependiente del tiempo en $S_\text{analyte}$ y/o $s_\text{noise}$ Debido a que la ecuación para $(S/N)_n$ es proporcional a la $\sqrt{n}$ , la mejora relativa en la relación señal/ruido disminuye a medida que $n$ aumenta; por ejemplo, 16 escaneos dan una $4 \times$ mejora en la relación señal/ruido, pero se necesitan 48 escaneos adicionales (para un total de 64 escaneos) para lograr una $8 \times$ mejora en la relación señal/ruido.

Filtros Suavizados Digitales

Una característica del ruido es que su magnitud fluctúa rápidamente en contraste con la señal subyacente. Esto lo vemos, por ejemplo, en la Figura $\PageIndex{1}$ donde la señal subyacente o bien permanece constante o aumenta o disminuye de manera constante mientras el ruido fluctúa caóticamente. Los filtros de suavizado digitales aprovechan esto al usar una función matemática para promediar los datos para un pequeño rango de puntos de datos consecutivos, reemplazando el valor medio del rango con la señal promedio sobre ese rango.

Filtros de Media Móvil

Para un filtro de promedio móvil, reemplazamos cada punto por la señal promedio para ese punto y un número igual de puntos a cada lado; así, un filtrado de media móvil tiene un ancho, $w$ , de 3, 5, 7,... puntos. Por ejemplo, supongamos que los primeros cinco puntos de una secuencia son

0.80

0.30

0.80

0.20

1.00

luego una media móvil de tres puntos ( $w = 3)$ devuelve valores de

0.63

0.43

0.67

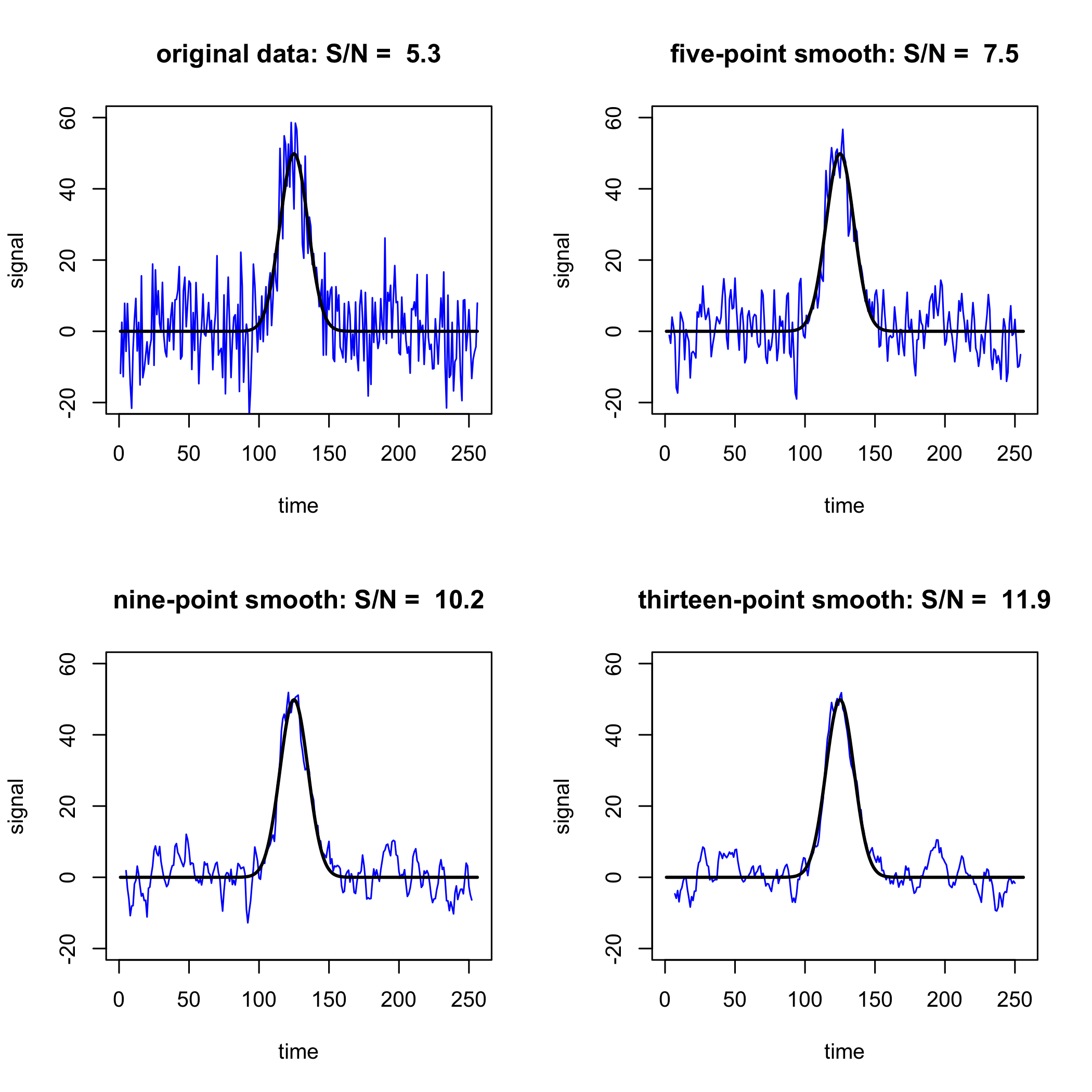
donde, por ejemplo, 0.63 es el promedio de 0.80, 0.30 y 0.80. Tenga en cuenta que perdemos $(w - 1)/2 = (3 - 1)/2 = 1$ puntos en cada extremo del conjunto de datos porque no tenemos un número suficiente de puntos de datos para completar un cálculo para el primer y el último punto. La figura $\PageIndex{2}$ muestra la mejora en la $S/N$ relación al usar filtros de promedio móvil con anchuras de 5, 9 y 13.

Figura $\PageIndex{2}$ : Mejora en la relación señal/ruido utilizando filtros de promedio móvil con rangos de 5, 9 y 13 sobre los datos originales mostrados en el cuadrante superior izquierdo. Cada gráfica muestra la señal ruidosa en azul con la señal pura superpuesta en negro.

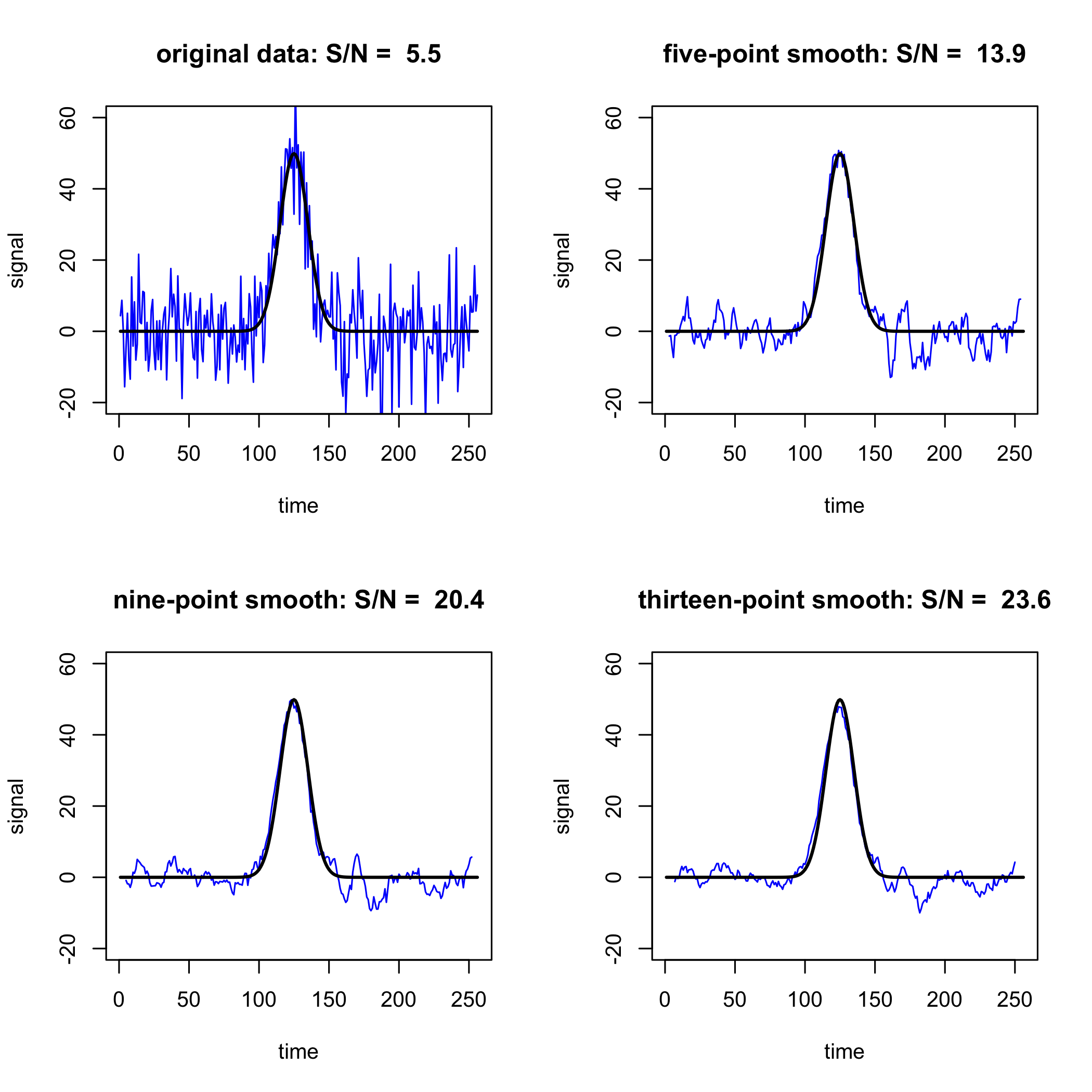
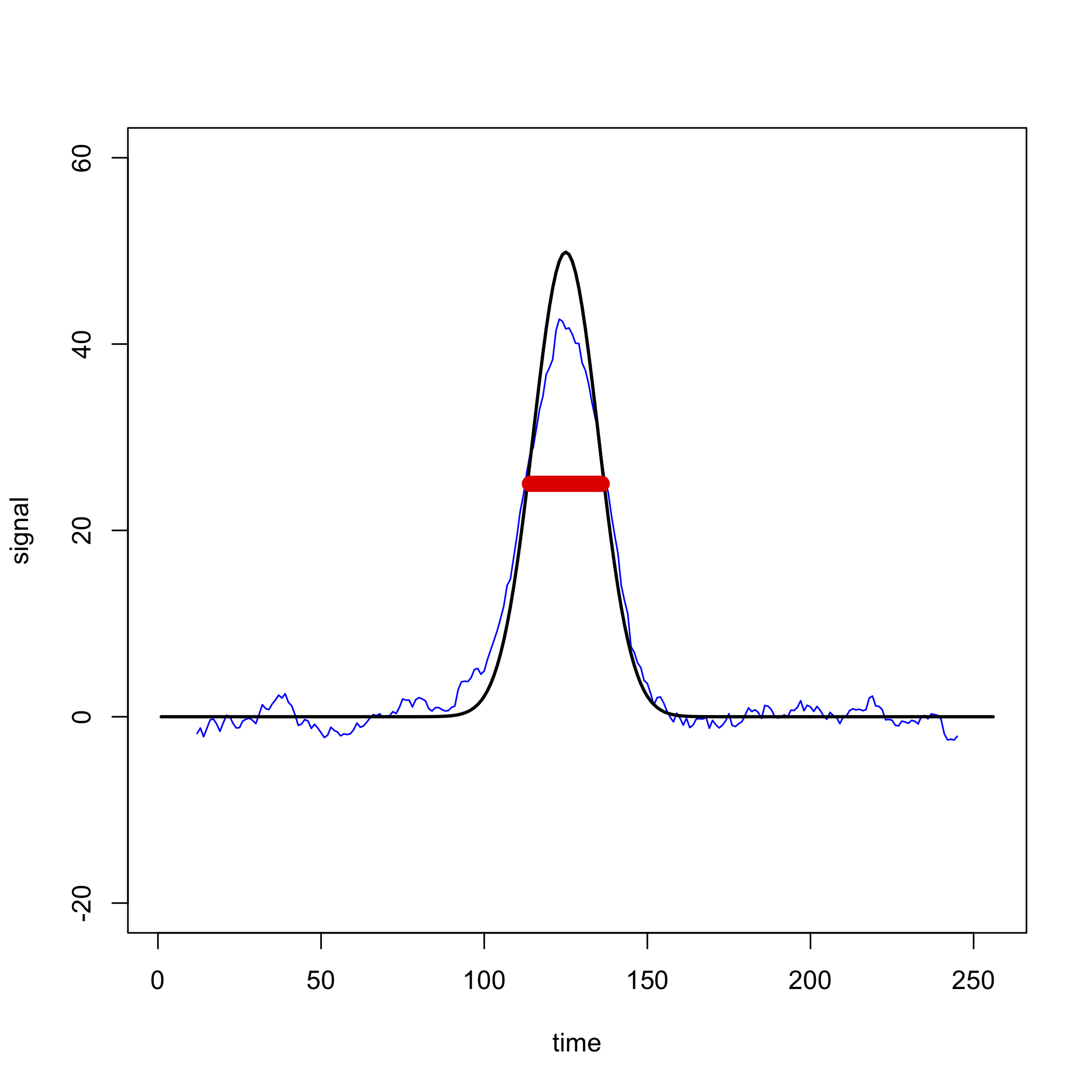
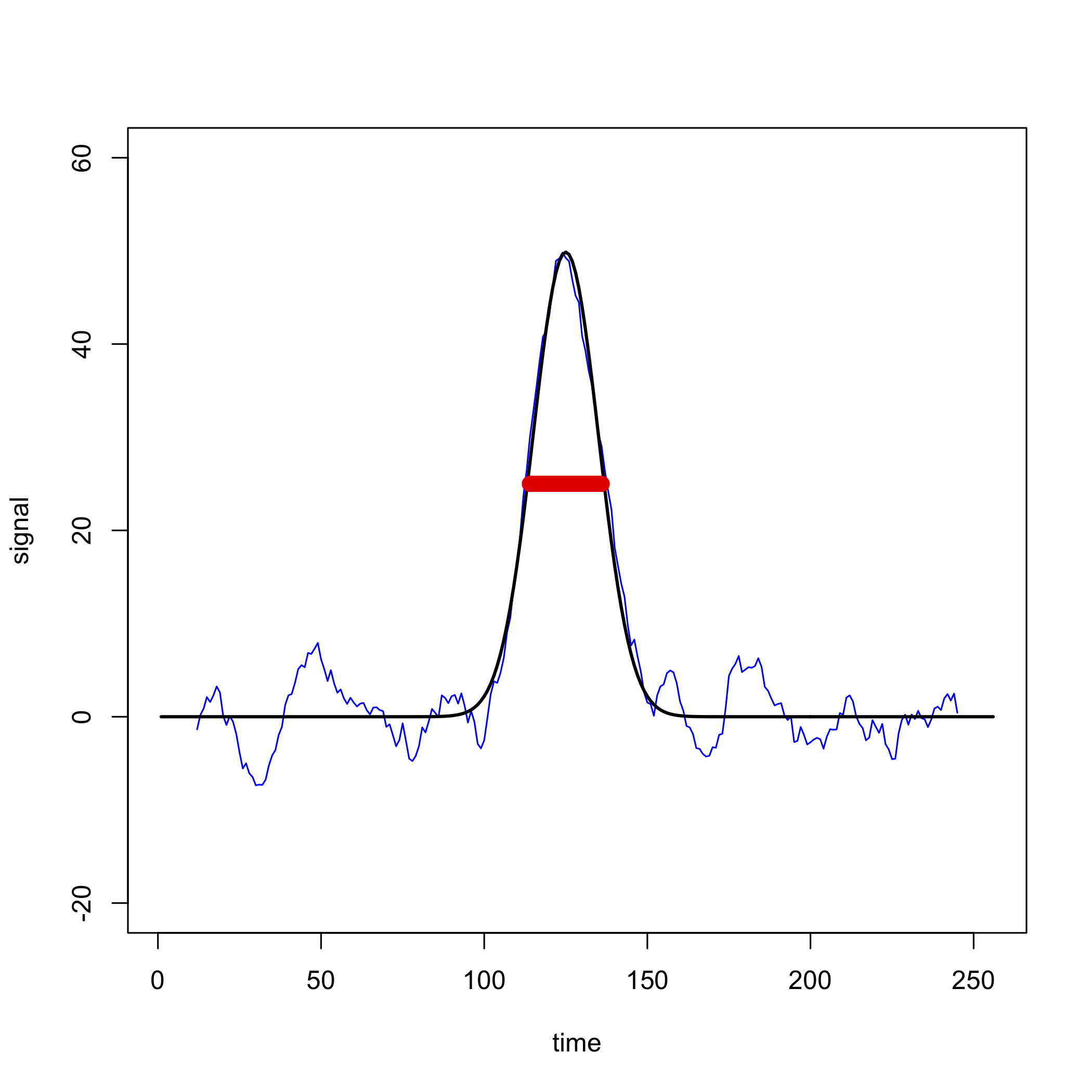
Una limitación a un filtro de media móvil es que distorsiona los datos originales al eliminar puntos de ambos extremos, aunque esto no es una preocupación seria si los puntos en cuestión son solo ruido. De mayor preocupación es la distorsión en la altura de una señal si utilizamos un rango que es demasiado ancho; por ejemplo, la Figura $\PageIndex{3}$ , muestra cómo un filtro de promedio móvil de 23 puntos (mostrado en azul) aplicado a la señal ruidosa en el cuadrante superior izquierdo de la Figura $\PageIndex{2}$ , reduce la altura de la señal original (mostrada en negro). Debido a que el ancho del filtro, mostrado por la barra roja, es similar al ancho del pico, a medida que el filtro pasa a través del pico, reduce sistemáticamente la señal promediando valores que son en su mayoría más pequeños que la señal máxima.

Figura $\PageIndex{3}$ : Ejemplo que muestra cómo un filtro de promedio móvil puede distorsionar la señal cuando se aplica a la señal ruidosa en el cuadrante superior izquierdo de la Figura $\PageIndex{2}$ . La señal pura original se muestra en negro y la señal después de aplicar un filtro de promedio móvil de 23 puntos se muestra en azul. El ancho del filtro de media móvil se muestra mediante la barra roja.

Filtros Savitzky-Golay

Un filtro de promedio móvil pondera todos los puntos por igual; es decir, los puntos cercanos a los bordes del filtro contribuyen al promedio como un nivel igual a los puntos cercanos al centro del filtro. Un filtro Savitzky-Golay utiliza un modelo polinómico que pondera cada punto de manera diferente, colocando más peso en los puntos cercanos al centro del filtro y menos peso en los puntos en el borde del filtro. Los valores específicos dependen del tamaño de la ventana y del modelo polinómico; por ejemplo, un filtro de cinco puntos que utiliza un polinomio de segundo orden tiene pesos de

$-3/35 \quad \quad 12/35 \quad \quad 17/35 \quad \quad 12/35 \quad \quad -3/35 \nonumber$

Por ejemplo, supongamos que los primeros cinco puntos de una secuencia son

0.80

0.30

0.80

0.20

1.00

entonces este filtro Savitzky-Golay devuelve valores de

0.41

donde, por ejemplo, el valor para el punto medio es

$0.80 \times \frac{-3}{35} + 0.30 \times \frac{12}{35} + 0.80 \times \frac{17}{35} + 0.20 \times \frac{12}{35} + 1.00 \times \frac{-3}{35} = 0.406 \approx 0.41 \nonumber$

Tenga en cuenta que perdemos $(w - 1)/2 = (5 - 1)/2 = 2$ puntos en cada extremo del conjunto de datos, donde w es el rango del filtro, porque no tenemos un número suficiente de puntos de datos para completar los cálculos. Para otros filtros de alisado Savitzky-Golay, véase Savitzky, A.; Golay, M. J. E. Anal Chem, 1964, 36, 1627-1639. La figura $\PageIndex{4}$ muestra la mejora en la $S/N$ relación al usar filtros Savitzky-Golay usando un polinomio de segundo orden con 5, 9 y 13 puntos.

Figura $\PageIndex{4}$ : Mejora en la relación señal/ruido utilizando filtros Savitzky-Golay de rangos de 5, 9 y 13 sobre los datos originales mostrados en el cuadrante superior izquierdo. Cada gráfica muestra la señal ruidosa en azul con la señal pura superpuesta en negro.

Debido a que un filtro Savitzky-Golay pondera los puntos de manera diferente que lo hace un filtro de suavizado de promedio móvil, un filtro Savitzky-Golay introduce menos distorsión en la señal, como vemos en la siguiente figura.

Figura $\PageIndex{5}$ : Un filtro Savitzky-Golay es menos agresivo que un filtro de media móvil. Aplicar un filtro Savitzky-Golay de 23 puntos a la señal ruidosa en el cuadrante superior izquierdo de la Figura $\PageIndex{4}$ da como resultado poca distorsión de la señal. Contraste esto con la Figura $\PageIndex{3}$ donde un filtro de promedio móvil de 23 puntos da como resultado una distorsión sustancial de la señal. La señal pura original se muestra en negro y la señal después de aplicar un filtro Savitzky-Golay de 23 puntos se muestra en azul. El ancho del filtro Savitzky-Golay se muestra con la barra roja.

Filtrado de Fourier

Este enfoque para mejorar la relación señal/ruido aprovecha una técnica matemática llamada transformada de Fourier (FT). La base de una transformada de Fourier es que podemos expresar una señal en dos dominios separados. En el primer dominio la señal se caracteriza por uno o más picos, cada uno definido por su posición, su ancho y su área; esto se denomina dominio de frecuencia. En el segundo dominio, que se llama dominio del tiempo, la señal consiste en un conjunto de oscilaciones, cada una definida por su frecuencia, su amplitud y su tasa de decaimiento. La transformada de Fourier, y la transformada inversa de Fourier, nos permiten movernos entre estos dos dominios.

Nota

Los detalles matemáticos detrás de la transformada de Fourier están más allá del nivel de este libro de texto; para un tratamiento más profundo, consulte los recursos de este capítulo.

La figura $\PageIndex{6a}$ muestra un único pico en el dominio de frecuencia y la figura $\PageIndex{6b}$ muestra su señal equivalente en el dominio del tiempo. Hay correlaciones entre los dos dominios:

cuanto más lejos esté un pico en el dominio de la frecuencia del origen, mayor será la frecuencia de oscilación correspondiente en el dominio del tiempo
cuanto más amplio sea el ancho de un pico en el dominio de frecuencia, más rápida será su tasa de desintegración en el dominio del tiempo
cuanto mayor sea el área bajo un pico en el dominio de la frecuencia, mayor será su intensidad inicial en el dominio del tiempo

Figura $\PageIndex{6}$ : La gráfica de (a) muestra un dominio de frecuencia que consiste en un solo pico definido por su posición a lo largo del eje x, su ancho y su área. La gráfica en (b) muestra el dominio de tiempo correspondiente que consiste en una única señal oscilante definida por su frecuencia de oscilación, su intensidad inicial y su tasa de decaimiento.

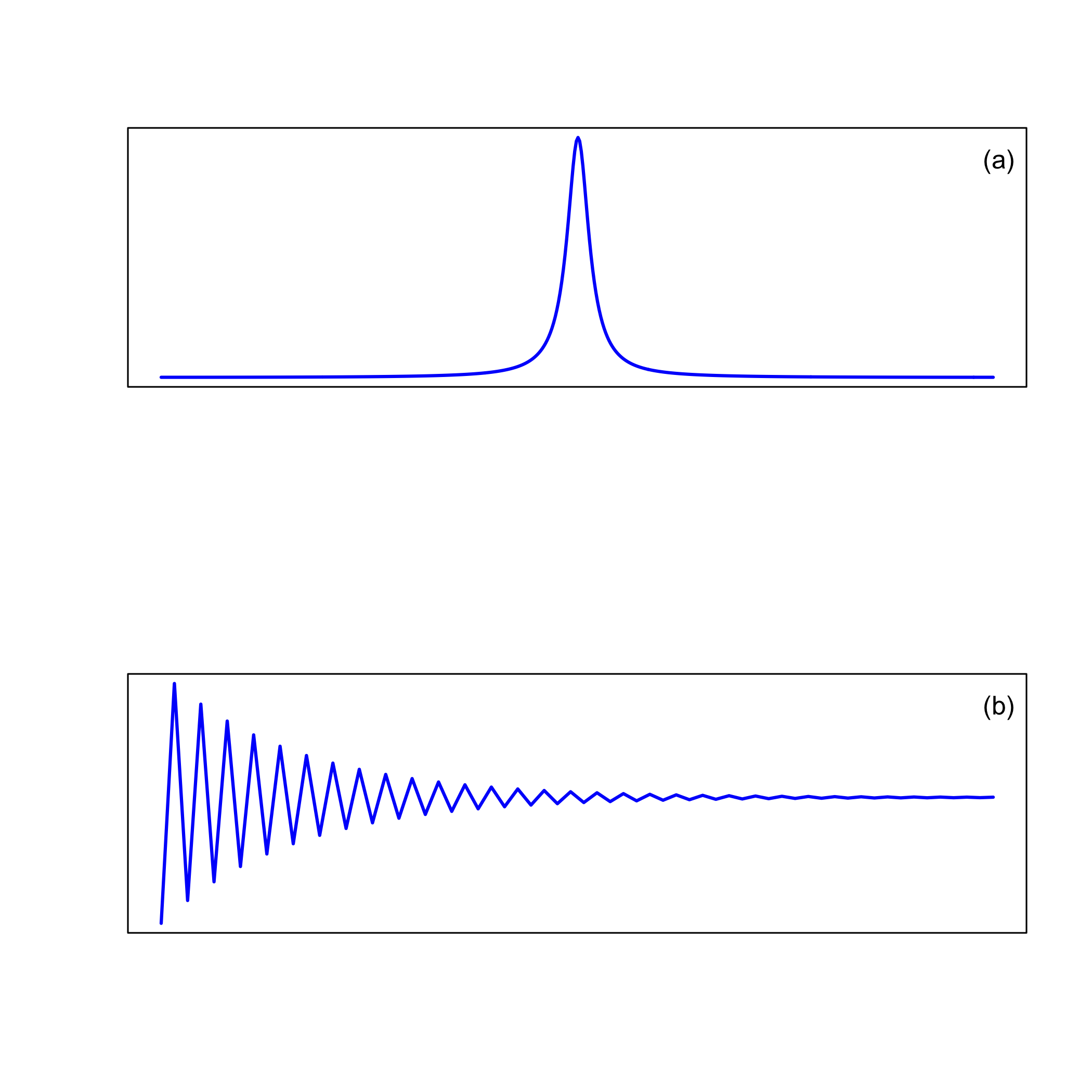
Podemos usar una transformada de Fourier para mejorar la relación señal/ruido porque la señal es un único pico ancho y el ruido aparece como una multitud de picos muy estrechos. Como se señaló anteriormente, un pico amplio en el dominio de la frecuencia tiene una señal de decaimiento rápido en el dominio del tiempo, lo que significa que mientras que el comienzo de la señal de dominio de tiempo incluye contribuciones de la señal y el ruido, la última parte de la señal de dominio de tiempo incluye contribuciones del ruido solamente. La siguiente figura muestra cómo podemos aprovechar esto para reducir el ruido y mejorar la relación señal/ruido para la señal ruidosa en la Figura $\PageIndex{7a}$ , que tiene 256 puntos a lo largo del eje x y tiene una relación señal/ruido de 5.1. Primero, utilizamos la transformada de Fourier para convertir su dominio original en el nuevo dominio, cuyos primeros 128 puntos se muestran en la Figura $\PageIndex{7b}$ (nota: la primera mitad de los datos contiene la misma información que la segunda mitad de los datos, por lo que solo necesitamos mirar la primera mitad de los datos). Los puntos al inicio están dominados por la señal, razón por la cual hay una disminución sistemática en la intensidad de las oscilaciones; los puntos restantes están dominados por el ruido, razón por la cual la variación en la intensidad es aleatoria. Para filtrar el ruido retenemos los primeros 24 puntos tal como están y establecemos las intensidades de los puntos restantes a cero (la elección de cuántos puntos retener puede requerir algún ajuste). Como se muestra en la Figura $\PageIndex{7c}$ , repetimos esto para los 128 puntos restantes, conservando los últimos 24 puntos tal como están. Finalmente, utilizamos una transformada inversa de Fourier para regresar a nuestro dominio original, con el resultado en la Figura $\PageIndex{7d}$ , con la relación señal/ruido mejorando de 5. 1 para la señal ruidosa original a 11.2 para la señal filtrada.

Figura $\PageIndex{7}$ : Ejemplo de eliminación de ruido usando un filtro de Fourier. La señal ruidosa original con $S/N = 5.1$ se muestra en (a) y es similar a la señal ruidosa en la Figura $\PageIndex{2a}$ y Figura $\PageIndex{4a}$ . La primera mitad de los datos transformados de Fourier se muestra en (b). Los datos transformados de Fourier se muestran en (c) después de poner a cero todos menos los primeros y los últimos 24 puntos. Volviendo al dominio original da la señal filtrada final con $S/N = 11.1$ .

Search

Text Color

Text Size

Margin Size

Font Type

Nota

Promedio de señal

Filtros Suavizados Digitales

Filtros de Media Móvil

Filtros Savitzky-Golay

Filtrado de Fourier

Nota

Support Center

How can we help?