1.8: Revisión de Matrices

Definiciones

Una$n \times m$ matriz es una matriz bidimensional de números con$n$ filas y$m$ columnas. Los enteros$n$ y$m$ se llaman las dimensiones de la matriz. Si$n = m$ entonces la matriz es cuadrada. Los números en la matriz se conocen como elementos de la matriz (o simplemente elementos) y generalmente se les da subíndices para significar su posición en la matriz, por ejemplo, un elemento$a_{ij}$ ocuparía la$i^{th}$ fila y$j^{th}$ columna de la matriz. Por ejemplo:

$$M = \left(\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right) \label{8.1}$$

es una$3 \times 3$ matriz con$a_{11}=1$,$a_{12}=2$,$a_{13}=3$,$a_{21}=4$ etc

En una matriz cuadrada, los elementos diagonales son aquellos para los cuales$i$ =$j$ (los números$1$$5$,, y$9$ en el ejemplo anterior). Los elementos fuera de diagonal son aquellos para los cuales$i \neq j$ ($2$$3$$4$,$6$,$7$,, y$8$ en el ejemplo anterior). Si todos los elementos fuera de la diagonal son iguales a cero entonces tenemos una matriz diagonal. Veremos más adelante que las matrices diagonales son de considerable importancia en la teoría de grupos.

Una matriz unitaria o matriz de identidad (generalmente dada el símbolo$I$) es una matriz diagonal en la que todos los elementos diagonales son iguales a$1$. Una matriz unitaria que actúa sobre otra matriz no tiene ningún efecto —es lo mismo que la operación de identidad en la teoría de grupos y es análoga a multiplicar un número por$1$ en la aritmética cotidiana.

La transposición$A^T$ de una matriz$A$ es la matriz que resulta de intercambiar todas las filas y columnas. Una matriz simétrica es la misma que su transposición ($A^T=A$es decir,$a_{ij} = a_{ji}$ para todos los valores de$i$ y$j$). La transpuesta de la matriz$M$ anterior (que no es simétrica) es

$$M^{T} = \left(\begin{array}{ccc} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{array}\right) \label{8.2}$$

La suma de los elementos diagonales en una matriz cuadrada se denomina traza (o carácter) de la matriz (para la matriz anterior, la traza es$\chi = 1 + 5 + 9 = 15$). Las trazas de matrices que representan operaciones de simetría resultarán de gran importancia en la teoría de grupos.

Un vector es solo un caso especial de una matriz en la que una de las dimensiones es igual a$1$. Una$n \times 1$ matriz es un vector de columna; una$1 \times m$ matriz es un vector de fila. Los componentes de un vector generalmente solo se etiquetan con un índice. Un vector unitario tiene un elemento igual a$1$ y los demás igual a cero (es lo mismo que una fila o columna de una matriz de identidad). Podemos extender la idea más allá para decir que un solo número es una matriz (o vector) de dimensión$1 \times 1$.

Álgebra Matriz

1. Se pueden sumar o restar dos matrices con las mismas dimensiones sumando o restando los elementos que ocupan la misma posición en cada matriz. e.g.

$$A = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 2 &1 \\ 3 & 2 & 0 \end{pmatrix} \label{8.3}$$

$$B = \begin{pmatrix} 2 & 0 & -2 \\ 1 & 0 & 1 \\ 1 & -1 & 0 \end{pmatrix} \label{8.4}$$

$$A + B = \begin{pmatrix} 3 & 0 & 0 \\ 3 & 2 & 2 \\ 4 & 1 & 0 \end{pmatrix} \label{8.5}$$

$$A - B = \begin{pmatrix} -1 & 0 & 4 \\ 1 & 2 & 0 \\ 2 & 3 & 0 \end{pmatrix} \label{8.6}$$

2. Una matriz se puede multiplicar por una constante multiplicando cada elemento por la constante.

$$4B = \left(\begin{array}{ccc} 8 & 0 & -8 \\ 4 & 0 & 4 \\ 4 & -4 & 0 \end{array}\right) \label{8.7}$$

$$3A = \left(\begin{array}{ccc} 3 & 0 & 6 \\ 6 & 6 & 3 \\ 9 & 6 & 0 \end{array}\right) \label{8.8}$$

3. Dos matrices se pueden multiplicar juntas siempre que el número de columnas de la primera matriz sea el mismo que el número de filas de la segunda matriz, es decir, una$n \times m$ matriz se puede multiplicar por una$m \times l$ matriz. La matriz resultante tendrá dimensiones$n \times l$. Para encontrar el elemento$a_{ij}$ en la matriz del producto, tomamos el producto de punto de fila$i$ de la primera matriz y columna$j$ de la segunda matriz (es decir, multiplicamos elementos consecutivos juntos de la fila$i$ de la primera matriz y columna$j$ de la segunda matriz y los agregamos juntos es decir$c_{ij}$ =$\Sigma_k$$a_{ik}$$b_{jk}$ por ejemplo en las$3 \times 3$ matrices$A$ y$B$ utilizados en los ejemplos anteriores, el primer elemento en la matriz del producto$C = AB$ es$c_{11}$ =$a_{11}$$b_{11}$ +$a_{12}$$b_{21}$ +$a_{13}$$b_{31}$

$$AB = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 2 & 1 \\ 3 & 2 & 0 \end{pmatrix} \begin{pmatrix} 2 & 0 & -2 \\ 1 & 0 & 1 \\ 1 & -1 & 0 \end{pmatrix} = \begin{pmatrix} 4 & -2 & -2 \\ 7 & -1 & -2 \\ 8 & 0 & -4 \end{pmatrix} \label{8.9}$$

Un ejemplo de una matriz que multiplica un vector es

$$A\textbf{v} = \begin{pmatrix} 1 & 0 & 2 \\ 2 & 2 & 1 \\ 3 & 2 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 7 \\ 9 \\ 7 \end{pmatrix} \label{8.10}$$

La multiplicación matricial no es generalmente conmutativa, una propiedad que refleja el comportamiento encontrado anteriormente para las operaciones de simetría dentro de un grupo de puntos.

Productos Directos

El producto directo de dos matrices (dado el símbolo$\otimes$) es un tipo especial de producto matricial que genera una matriz de mayor dimensionalidad si ambas matrices tienen una dimensión mayor a una. La forma más fácil de demostrar cómo construir un producto directo de dos matrices$A$ y$B$ es mediante un ejemplo:

$$\begin{align} A \otimes B &= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \otimes \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \\[4pt] &= \begin{pmatrix} a_{11}B & a_{12}B \\ a_{21}B & a_{22}B \end{pmatrix} \\[4pt] &= \begin{pmatrix} a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11} & a_{12}b_{12} \\ a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21} & a_{12}b_{22} \\ a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11} & a_{22}b_{21} \\ a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21} & a_{22}b_{22} \end{pmatrix} \label{8.11} \end{align}$$

Aunque esto pueda parecer una operación algo extraña de llevar a cabo, los productos directos surgen mucho en la teoría de grupos.

Matrices inversas y determinantes

Si dos matrices cuadradas$A$ y$B$ se multiplican juntas para dar la matriz de identidad I (i.e.$AB = I$) entonces se dice que$B$ es la inversa de$A$ (escrita$A^{-1}$). Si$B$ es la inversa de$A$ entonces$A$ es también la inversa de$B$. Recordemos que una de las condiciones impuestas a las operaciones de simetría en un grupo es que cada operación debe tener una inversa. Se deduce por analogía que cualquier matriz que utilicemos para representar elementos de simetría también debe tener inversas. Resulta que una matriz cuadrada sólo tiene una inversa si su determinante es distinto de cero. Por esta razón (y otras que se harán evidentes más adelante cuando necesitemos resolver ecuaciones que involucren matrices) necesitamos aprender un poco sobre los determinantes matriciales y sus propiedades.

Por cada matriz cuadrada, hay una función única de todos los elementos que produce un solo número llamado determinante. Al principio probablemente no será particularmente obvio por qué este número debería ser útil, pero los determinantes matriciales son de gran importancia tanto en matemáticas puras como en varias áreas de la ciencia. Históricamente, los determinantes estaban en realidad alrededor antes de las matrices. Surgieron originalmente como una propiedad de un sistema de ecuaciones lineales que 'determinaban' si el sistema tenía una solución única. Como veremos más adelante, cuando tal sistema de ecuaciones se refunda como una ecuación matricial esta propiedad se traslada al determinante de la matriz.

Hay dos definiciones diferentes de un determinante, una geométrica y otra algebraica. En la interpretación geométrica, consideramos los números a lo largo de cada fila de una$n \times n$ matriz como coordenadas en el espacio$n$ -dimensional. En una matriz unidimensional (es decir, un número), solo hay una coordenada, y el determinante puede interpretarse como la longitud (firmada) de un vector desde el origen hasta este punto. Para una$2 \times 2$ matriz tenemos dos coordenadas en un plano, y el determinante es el área (firmada) del paralelogramo que incluye estos dos puntos y el origen. Para una$3 \times 3$ matriz el determinante es el volumen (firmado) del paralelepípedo que incluye los tres puntos (en el espacio tridimensional) definidos por la matriz y el origen. Esto se ilustra a continuación. La idea se extiende hasta dimensiones superiores de manera similar. Entonces, en cierto sentido, el determinante está relacionado con el tamaño de una matriz.

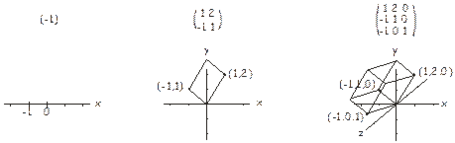
La definición algebraica del determinante de una$nxn$ matriz es una suma sobre todos los posibles productos (permutaciones) de n elementos tomados de diferentes filas y columnas. El número de términos en la suma es$n!$, el número de posibles permutaciones de$n$ valores (es decir,$2$ para una$2 \times 2$ matriz,$6$ para una$3 \times 3$ matriz, etc.). A cada término en la suma se le da un signo positivo o negativo dependiendo de si el número de inversiones de permutación en el producto es par o impar. Una inversión de permutación es solo un par de elementos que están fuera de orden cuando se describen por sus índices. Por ejemplo, para un conjunto de cuatro elementos$\begin{pmatrix} a_1, a_2, a_3, a_4 \end{pmatrix}$, la permutación$a_1 a_2 a_3 a_4$ tiene todos los elementos en su orden correcto (es decir, en orden de índice creciente). Sin embargo, la permutación$a_2 a_4 a_1 a_3$ contiene las inversiones de permutación$a_2 a_1$,$a_4 a_1$,$a_4 a_3$.

Por ejemplo, para una matriz bidimensional

$$\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \label{8.12}$$

donde los subíndices etiquetan las posiciones de fila y columna de los elementos, existen$2$ posibles productos/permutaciones que involucran elementos de diferentes filas y columnas,$a_{11}$$a_{22}$ y$a_{12}$$a_{21}$. En el segundo término, hay una inversión de permutación que involucra a los índices de columna$2$ y$1$ (las inversiones de permutación que involucren los índices de fila y columna deben buscarse por separado) por lo que este término toma un signo negativo, y el determinante es$a_{11}$$a_{22}$ -$a_{12}$$a_{21}$.

Para una$3 \times 3$ matriz

$$\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \label{8.13}$$

las posibles combinaciones de elementos de diferentes filas y columnas, junto con el signo del número de permutaciones requeridas para poner sus índices en orden numérico son:

$$\begin{array}{rl}a_{11} a_{22} a_{33} & (0 \: \text{inversions}) \\ -a_{11} a_{23} a_{32} & (1 \: \text{inversion -} \: 3>2 \: \text{in the column indices}) \\ -a_{12} a_{21} a_{33} & (1 \: \text{inversion -} \: 2>1 \: \text{in the column indices}) \\ a_{12} a_{23} a_{31} & (2 \: \text{inversions -} \: 2>1 \: \text{and} \: 3>1 \: \text{in the column indices}) \\ a_{13} a_{21} a_{32} & (2 \: \text{inversions -} \: 3>1 \: \text{and} \: 3>2 \: \text{in the column indices}) \\ -a_{13} a_{22} a_{31} & (3 \: \text{inversions -} \: 3>2, 3>1, \: \text{and} \: 2>1 \: \text{in the column indices}) \end{array} \label{8.14}$$

y el determinante es simplemente la suma de estos términos.

Todo esto puede parecer un poco complicado, pero en la práctica existe un procedimiento bastante sistemático para calcular los determinantes. El determinante de una matriz$A$ suele escribirse det ($A$) o |$a$ |.

Para una$2 \times 2$ matriz

$$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}; det(A) = |A| = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc \label{8.15}$$

Para una$3 \times 3$ matriz

$$B = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}; det(B) = a\begin{vmatrix} e & f \\ h & i \end{vmatrix} - b\begin{vmatrix} d & f \\ g & i \end{vmatrix} + c\begin{vmatrix} d & e \\ g & h \end{vmatrix} \label{8.16}$$

Para una$4x4$ matriz

$$C = \begin{pmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{pmatrix}; det(C) = a\begin{vmatrix} f & g & h \\ j & k & l \\ n & o & p \end{vmatrix} - b\begin{vmatrix} e & g & h \\ i & k & l \\ m & o & p \end{vmatrix} + c\begin{vmatrix} e & f & h \\ i & j & l \\ m & n & p \end{vmatrix} - d\begin{vmatrix} e & f & g \\ i & j & k \\ m & n & o \end{vmatrix} \label{8.17}$$

y así sucesivamente en dimensiones superiores. Tenga en cuenta que las submatrices en el$3 \times 3$ ejemplo anterior son solo las matrices formadas a partir de la matriz original$B$ que no incluyen ningún elemento de la misma fila o columna como los factores premultiplicadores de la primera fila.

Los determinantes de matriz tienen una serie de propiedades importantes:

1. El determinante de la matriz de identidad es$1$.

$$e.g. \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = \begin{vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = 1 \label{8.18}$$

2. El determinante de una matriz es el mismo que el determinante de su transposición, es decir, det ($a$) = det ($A^{T}$)

$$e.g. \begin{vmatrix} a & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & c \\ b & d \end{vmatrix} \label{8.19}$$

3. El determinante cambia de signo cuando se intercambian dos filas o dos columnas cualesquiera

$$e.g. \begin{vmatrix} a & b \\ c & d \end{vmatrix} = -\begin{vmatrix} b & a \\ d & c \end{vmatrix} = -\begin{vmatrix} c & d \\ a & b \end{vmatrix} = \begin{vmatrix} d & c \\ b & a \end{vmatrix} \label{8.20}$$

4. El determinante es cero si alguna fila o columna es completamente cero, o si dos filas o columnas cualesquiera son iguales o un múltiplo entre sí.

$$e.g. \begin{vmatrix} 1 & 2 \\ 0 & 0 \end{vmatrix} = 0, \begin{vmatrix} 1 & 2 \\ 2 & 4 \end{vmatrix} = 0 \label{8.21}$$

5. El determinante no cambia al agregar cualquier combinación lineal de filas (o columnas) a otra fila (o columna).
6. El determinante del producto de dos matrices es el mismo que el producto de los determinantes de las dos matrices es decir, det ($AB$) = det ($A$) det ($B$).

El requisito de que para que una matriz tenga una inversa debe tener un determinante distinto de cero se desprende de la propiedad vi). Como se mencionó anteriormente, el producto de una matriz y su inversa produce la matriz de identidad I. Por lo tanto, tenemos:

$$\begin{array}{rcl} det(A^{-1} A) = det(A^{-1}) det(A) & = & det(I) \\ det(A^{-1}) & = & det(I)/det(A) = 1/det(A) \end{array} \label{8.22}$$

De ello se deduce que una matriz sólo$A$ puede tener una inversa si su determinante es distinto de cero, de lo contrario el determinante de su inversa sería indefinido.