7.3: Propiedades térmicas

Por conveniencia en derivaciones a seguir, aquí se repiten expresiones del Cap. 5 que se aplican a procesos en un sistema cerrado en ausencia de trabajo de no expansión (i.e.,\(w^{\prime}=0\)). Para un proceso a volumen constante tenemos\(^{3}\)
\ [
\ mathrm {d} U=\ mathrm {d} q\ quad C_ {V} =\ left (\ frac {\ partial U} {\ partial T}\ right) _ {V}
\]

y para un proceso a presión constante tenemos\({ }^{4}\)
\ [
\ mathrm {d} H=\ mathrm {d} q\ quad C_ {p} =\ left (\ frac {\ partial H} {\ partial T}\ right) _ {p}
\]

Un sistema cerrado de un componente en una sola fase tiene sólo dos variables independientes. En tal sistema, las derivadas parciales anteriores son definiciones completas e inequívocas de\(C_{V}\) y\(C_{p}\) porque se expresan con dos variables independientes-\(T\) y\(V\) para\(C_{V}\),\(T\) y\(p\) para\(C_{p}\). Como se menciona en la página 146, habría que especificar condiciones adicionales para definir\(C_{V}\) para un sistema más complicado; lo mismo es cierto para\(C_{p}\).

Para un sistema cerrado de un gas ideal tenemos 5
\ [
C_ {V} =\ frac {\ mathrm {d} U} {\ mathrm {~d} T}\ quad C_ {p} =\ frac {\ mathrm {d} H} {\ mathrm {~d} T}
\]

7.3.1 La relación entre\(C_{V, \mathrm{~m}}\) y\(C_{p, \mathrm{~m}}\)

El valor de\(C_{p, \mathrm{~m}}\) para una sustancia es mayor que\(C_{V, \mathrm{~m}}\). La derivación es simple en el caso de una cantidad fija de un gas ideal. Usando sustituciones de la Ec. 7.3.3, escribimos

\ [
C_ {p} -C_ {V} =\ frac {\ mathrm {d} H} {\ mathrm {~d} T} -\ frac {\ mathrm {d} U} {\ mathrm {~d} T} =\ frac {\ mathrm {d} (H-U)} {\ mathrm {d} T} =\ frac {\ mathrm {d} (p V)} {\ mathrm {d} T} =n R
\]

La división por\(n\) para obtener cantidades molares y el reordenamiento luego da

\ [
C_ {p,\ mathrm {~m}} =C_ {V,\ mathrm {~m}} +R
\]

Para cualquier fase en general, procedemos de la siguiente manera. Primero escribimos

\ [
C_ {p} =\ izquierda (\ frac {\ H parcial} {\ T parcial}\ derecha) _ {p} =\ izquierda [\ frac {\ parcial (U+p V)} {\ T parcial}\ derecha] _ {p} =\ izquierda (\ frac {\ parcial U} {\ parcial}\ derecha) _ {p} +p\ izquierda (\ frac {parcial\ V} {\ T parcial}\ derecha) _ {p}
\]

Luego escribimos el diferencial total de\(U\) con\(T\) y\(V\) como variables independientes e identificamos uno de los coeficientes como\(C_{V}\):

\ [
\ mathrm {d} U=\ izquierda (\ frac {\ U parcial} {\ T parcial}\ derecha) _ {V}\ mathrm {~d} T+\ izquierda (\ frac {\ U parcial} {\ V parcial}\ derecha) _ {T}\ mathrm {~d} V=C_ {V}\ mathrm {~d} T+\ izquierda (\ frac {\ U parcial} {\ V parcial}\ derecha) _ {T}\ mathrm {~d} V
\]

Cuando dividimos ambos lados de la ecuación anterior por\(\mathrm{d} T\) e imponemos una condición de constante\(p\), obtenemos

\ [
\ izquierda (\ frac {\ U parcial} {\ T parcial}\ derecha) _ {p} =C_ {V} +\ izquierda (\ frac {\ U parcial} {\ V parcial}\ derecha) _ {T}\ izquierda (\ frac {\ V parcial} {\ T parcial}\ derecha) _ {p}
\]

Sustitución de esta expresión por\(C_{p}\) rendimientos\((\partial U / \partial T)_{p}\) en la ecuación

\ [
C_ {p} =C_ {V} +\ izquierda [\ izquierda (\ frac {\ U parcial} {\ V parcial}\ derecha) _ {T} +p\ derecha]\ izquierda (\ frac {\ V parcial} {\ T parcial}\ derecha) _ {p}
\]

Finalmente establecemos la derivada parcial\((\partial U / \partial V)_{T}\) (la presión interna) igual a\(\left(\alpha T / \kappa_{T}\right)-p\) (Ec. 7.2.4) e\((\partial V / \partial T)_{p}\) igual\(\alpha V\) a para obtener

\ [
C_ {p} =C_ {V} +\ frac {\ alfa^ {2} T V} {\ kappa_ {T}}
\]

y\(n\) dividirlo para obtener cantidades molares:

\ [
C_ {p,\ mathrm {~m}} =C_ {V,\ mathrm {~m}} +\ frac {\ alpha^ {2} T V_ {\ mathrm {m}}} {\ kappa_ {T}}
\]

Ya que la cantidad\(\alpha^{2} T V_{\mathrm{m}} / \kappa_{T}\) debe ser positiva,\(C_{p, \mathrm{~m}}\) es mayor que\(C_{V, \mathrm{~m}}\).

7.3.2 La medición de las capacidades térmicas

El método más preciso para evaluar la capacidad calorífica de una fase es medir el cambio de temperatura resultante del calentamiento con trabajo eléctrico. El procedimiento en general se llama calorimetría, y el aparato que contiene la fase de interés y el calentador eléctrico es un calorímetro. A continuación se describen los principios de tres tipos de calorímetros de uso común con calefacción eléctrica.

Calorímetros adiabáticos

Un calorímetro adiabático está diseñado para tener un flujo de calor insignificante hacia o desde sus alrededores. El calorímetro contiene la fase de interés, mantenida a volumen constante o presión constante, y también un calentador eléctrico y un dispositivo de medición de temperatura como un termómetro de resistencia de platino, termistor u oscilador de cristal de cuarzo. El contenido se puede agitar para asegurar la uniformidad de la temperatura.

Para minimizar la conducción y convección, el calorímetro suele estar rodeado por una camisa separada por un entrehierro o un espacio evacuado. La superficie exterior del calorímetro y la superficie interna de la camisa pueden pulirse para minimizar la emisión de radiación de estas superficies. Estas medidas, sin embargo, no son suficientes para asegurar un límite completamente adiabático, ya que la energía puede ser transferida por calor a lo largo del hardware de montaje y a través de los cables eléctricos. Por lo tanto, la temperatura de la camisa, o de un blindaje metálico exterior, se ajusta a lo largo del transcurso del experimento para estar lo más cerca posible de la temperatura variable del calorímetro. Este objetivo se logra más fácilmente cuando el cambio de temperatura es lento.

Para realizar una medición de la capacidad calorífica, se pasa una corriente eléctrica constante a través del circuito del calentador durante un período de tiempo conocido. El sistema es el calorímetro y su contenido. El trabajo eléctrico\(w_{\text {el }}\) realizado en el sistema por el circuito calefactor se calcula a partir de la forma integrada de la Ec. \(3.8 .5\)en la página 91:\(w_{\mathrm{el}}=I^{2} R_{\mathrm{el}} \Delta t\), donde\(I\) esta la corriente electrica,\(R_{\mathrm{el}}\) es la resistencia electrica, y\(\Delta t\) es el intervalo de tiempo. Asumimos que el límite es adiabático y escribimos la primera ley en la forma

\ [
\ mathrm {d} u=-p\ mathrm {~d} V+\ mathrm {d} w_ {\ mathrm {el}} +\ mathrm {d} w_ {\ mathrm {cont}}
\]

donde\(-p \mathrm{~d} V\) está el trabajo de expansión y\(w_{\text {cont }}\) es cualquier trabajo mecánico continuo de agitación (el subíndice “cont” significa continuo). Si el trabajo eléctrico se realiza en el sistema por un

Figura\(7.3\): Curva de calentamiento típica de un calorimet adiabático

termómetro que utiliza un circuito eléctrico externo, como un termómetro de resistencia de platino, esta obra está incluida en\(w_{\text {cont }}\).

Considera primero un calorímetro adiabático en el que el proceso de calentamiento se lleve a cabo a volumen constante. No hay trabajo de expansión, y la Eq. \(7.3 .12\)se convierte

\ [
\ mathrm {d} U=\ mathrm {d} w_ {\ mathrm {el}} +\ mathrm {d} w_ {\ mathrm {cont}}
\] (constante\(V\))

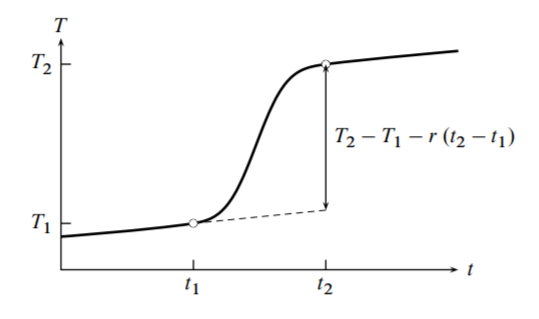
Un ejemplo de una curva de calentamiento medida (temperatura\(T\) en función del tiempo\(t\)) se muestra en la Fig. 7.3. Seleccionamos dos puntos en la curva de calentamiento, indicados en la figura por círculos abiertos. El tiempo\(t_{1}\) es en o poco antes del instante en que se cierra el circuito calentador y comienza el calentamiento eléctrico, y el tiempo\(t_{2}\) es después de que el circuito calentador se haya abierto y la pendiente de la curva se haya vuelto esencialmente constante.

En los periodos de tiempo anteriores\(t_{1}\) y posteriores\(t_{2}\), la temperatura puede exhibir una tasa de aumento lenta debido al trabajo continuo\(w_{\text {cont }}\) de agitación y medición de temperatura. Si este trabajo se realiza a una velocidad constante a lo largo del transcurso del experimento, la pendiente es constante y la misma en ambos periodos de tiempo como se muestra en la figura.

La relación entre la pendiente y la tasa de trabajo viene dada por una cantidad llamada el equivalente energético,\(\epsilon\). El equivalente energético es la capacidad calorífica del calorímetro bajo las condiciones de un experimento. La capacidad calorífica de un calorímetro de volumen constante viene dada por\(\epsilon=(\partial U / \partial T)_{V}\) (Ec. 5.6.1). Así, en los momentos anteriores\(t_{1}\) o posteriores\(t_{2}\), cuando\(w_{\text {el }}\) es cero e\(\mathrm{d} U\) igual\(w_{\text {cont }}\), la pendiente\(r\) de la curva de calentamiento viene dada por

\ [
r=\ frac {\ mathrm {d} T} {\ mathrm {~d} t} =\ frac {\ mathrm {d} T} {\ mathrm {~d} U}\ frac {\ mathrm {d} U} {\ mathrm {~d} t} =\ frac {1} {\ epsilon}\ frac {\ mathrm {d} w_ {\ text {cont}}} {\ mathrm {d} t}
\]

Por lo tanto, la tasa del trabajo continuo es\(\mathrm{d} w_{\text {cont }} / \mathrm{d} t=\epsilon r\). Esta tasa es constante a lo largo del experimento. En el intervalo de tiempo de\(t_{1}\) a\(t_{2}\), la cantidad total de trabajo continuo es\(w_{\text {cont }}=\epsilon r\left(t_{2}-t_{1}\right)\), donde\(r\) se mide la pendiente de la curva de calentamiento fuera de este intervalo de tiempo.

Para encontrar el equivalente energético, integramos la Ec. \(7.3 .13\)entre los dos puntos de la curva:

\ [
\ Delta u=w_ {\ mathrm {el}} +w_ {\ mathrm {cont}} =w_ {\ mathrm {el}} +\ epsilon r\ izquierda (t_ {2} -t_ {1}\ derecha)
\] (constante\(V\))

Entonces la capacidad calorífica promedio entre temperaturas\(T_{1}\) y\(T_{2}\) es

\ [
\ épsilon=\ frac {\ Delta U} {T_ {2} -T_ {1}} =\ frac {w_ {\ mathrm {el}} +\ épsilon r\ izquierda (t_ {2} -t_ {1}\ derecha)} {T_ {2} -T_ {1}}
\]

Resolviendo para\(\epsilon\), obtenemos

\ [
\ epsilon=\ frac {w_ {\ mathrm {el}}} {T_ {2} -T_ {1} -r\ izquierda (t_ {2} -t_ {1}\ derecha)}
\]

El valor del denominador en el lado derecho se indica mediante la línea vertical en la Fig. 7.3. Es el cambio de temperatura que se habría observado si se hubiera realizado la misma cantidad de trabajo eléctrico sin el trabajo continuo.

A continuación, considere el proceso de calentamiento en un calorímetro a presión constante. En este caso el cambio de entalpía viene dado por el\(\mathrm{d} H=\mathrm{d} U+p \mathrm{~d} V\) cual, con la sustitución de la Ec. 7.3.12, se convierte

\ [
\ mathrm {d} H=\ mathrm {d} w_ {\ mathrm {el}} +\ mathrm {d} w_ {\ mathrm {cont}}
\]
(constante\(p\))

Seguimos el mismo procedimiento que para el calorímetro de volumen constante, utilizando la Ec. \(7.3 .18\)en lugar de la Ec. \(7.3 .13\)y equiparando la energía equivalente\(\epsilon\) a\((\partial H / \partial T)_{p}\), la capacidad calorífica del calorímetro a presión constante (Ec. 5.6.3). Obtenemos la relación

\ [
\ Delta h=w_ {\ mathrm {el}} +w_ {\ mathrm {cont}} =w_ {\ mathrm {el}} +\ epsilon r\ izquierda (t_ {2} -t_ {1}\ derecha)
\]
(constante\(p\))

en lugar de la Ec. \(7.3 .15\)y terminar de nuevo con la expresión de la Eq. \(7.3 .17\)para\(\epsilon\).

El valor de\(\epsilon\) calculado a partir de la Ec. \(7.3 .17\)es un valor promedio para el intervalo de temperatura de\(T_{1}\) a\(T_{2}\), y podemos identificar este valor con la capacidad calorífica a la temperatura del punto medio del intervalo. Al tomar la diferencia de valores\(\epsilon\) medidos con y sin la fase de interés presente en el calorímetro, obtenemos\(C_{V}\) o\(C_{p}\) para la fase sola.

Puede parecer paradójico que podamos utilizar un proceso adiabático, uno sin calor, para evaluar una cantidad definida por el calor (capacidad calorífica\(=\mathrm{d} q / \mathrm{d} T\)). La explicación es que la energía transferida al calorímetro adiabático como obra eléctrica, y disipada completamente a la energía térmica, sustituye al calor que se necesitaría para el mismo cambio de estado sin trabajo eléctrico.

Calorímetros de chaqueta isotérmica

Un segundo tipo común de calorímetro es similar en construcción a un calorímetro adiabático, excepto que la camisa circundante se mantiene a temperatura constante. A veces se le llama calorímetro de isoperibol. Se realiza una corrección para la transferencia de calor resultante de la diferencia de temperatura a través del hueco que separa la camisa de la superficie exterior del calorímetro. Es importante al hacer esta corrección que la superficie exterior tenga una temperatura uniforme sin “puntos calientes”.

Supongamos que la superficie exterior del calorímetro tiene una temperatura uniforme\(T\) que varía con el tiempo, la temperatura de la camisa tiene un valor constante\(T_{\text {ext }}\), y la convección se ha eliminado al evacuar el hueco. Entonces la transferencia de calor es por conducción y radiación, y su velocidad

Figura Curva de calentamiento\(7.4\) típica de un calorímetro de camisa isotérmica

está dada por la ley de enfriamiento de Newton

\ [
\ frac {\ mathrm {d} q} {\ mathrm {~d} t} =-k\ izquierda (T-T_ {\ mathrm {ext}}\ derecha)
\]

donde\(k\) es una constante (la conductancia térmica). El calor fluye de un cuerpo más cálido a un cuerpo más frío, por lo que\(q / \mathrm{d} t\)\(T\) es positivo si es menor que\(T_{\text {ext }}\) y negativo si\(T\) es mayor que\(T_{\text {ext }}\).

Los posibles tipos de trabajo son los mismos que para el calorímetro adiabático: trabajo de expansión\(-p \mathrm{~d} V\), trabajo intermitente\(w_{\mathrm{el}}\) realizado por el circuito del calentador y trabajo continuo\(w_{\text {cont }}\). Al combinar la primera ley y la ecuación 7.3.20, obtenemos la siguiente relación para la velocidad a la que cambia la energía interna:

\ [
\ frac {\ mathrm {d} U} {\ mathrm {~d} t} =\ frac {\ mathrm {d} q} {\ mathrm {~d} t} +\ frac {\ mathrm {d} w} {\ mathrm {~d} t} =-k\ izquierda (T-T_ {\ mathrm {ext}}\ derecha) -p\ frac {\ mathrm {d} V} {\ mathrm {~d} t} +\ frac {\ mathrm {d} w_ {\ mathrm {el}}} {\ mathrm {d} t} +\ frac {\ mathrm {d} w_ {\ text {cont}}} {\ mathrm {d} t}
\]

Para calentar a volumen constante\((\mathrm{d} V / \mathrm{d} t=0)\), esta relación se convierte en

\ [
\ frac {\ mathrm {d} U} {\ mathrm {~d} t} =-k\ izquierda (T-T_ {\ mathrm {ext}}\ derecha) +\ frac {\ mathrm {d} w_ {\ mathrm {el}}} {\ mathrm {d} t} +\ frac {\ mathrm {d} w_ {\ mathrm {conrm {t}}} {\ mathrm {d} t}
\] (constante\(V\))

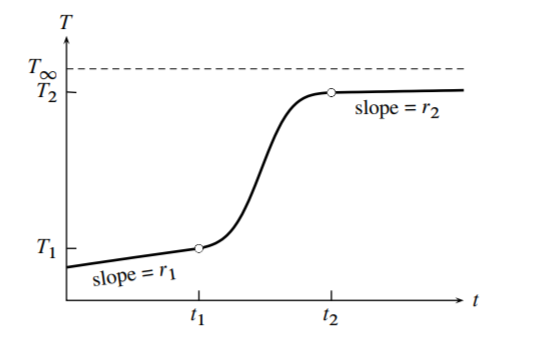
Un ejemplo de una curva de calentamiento se muestra en la Fig. 7.4. En contraste con la curva de la Fig. \(7.3\), las pendientes son diferentes antes y después del intervalo de calentamiento debido al cambio de la tasa de flujo de calor. Los tiempos\(t_{1}\) y\(t_{2}\) son antes y después de que el circuito del calentador esté cerrado. En cualquier intervalo de tiempo antes\(t_{1}\) o después del tiempo\(t_{2}\), el sistema se comporta como si se estuviera acercando a un estado estacionario de temperatura constante\(T_{\infty}\) (llamado temperatura de convergencia), que eventualmente alcanzaría si el experimento se continuara sin cerrar el circuito calentador. \(T_{\infty}\)es mayor que\(T_{\text {ext }}\) debido a la energía transferida al sistema por agitación y medición eléctrica de la temperatura. Al establecer\(\mathrm{d} U / \mathrm{d} t\) e\(\mathrm{d} w_{\mathrm{el}} / \mathrm{d} t\) igual a cero e\(T\) igual a\(T_{\infty}\) en la Ec. 7.3.22, obtenemos ʼ\(w_{\text {cont }} / \mathrm{d} t=k\left(T_{\infty}-T_{\text {ext }}\right) .\) Suponemos que d\(w_{\text {cont }} / \mathrm{d} t\) es constante. Sustituyendo esta expresión en la Ec. \(7.3 .22\)nos da una expresión general para la velocidad a la que\(U\) cambia en términos de las cantidades desconocidas\(k\) y\(T_{\infty}\):

\ [
\ frac {\ mathrm {d} U} {\ mathrm {~d} t} =-k\ izquierda (T-T_ {\ infty}\ derecha) +\ frac {\ mathrm {d} w_ {\ mathrm {el}}} {\ mathrm {d} t}
\]
(constante\(V\))

Esta relación es válida a lo largo del experimento, no sólo mientras el circuito calefactor esté cerrado. Si multiplicamos por\(\mathrm{d} t\) e integramos de\(t_{1}\) a\(t_{2}\), obtenemos el cambio de energía interna en el intervalo de tiempo de\(t_{1}\) a\(t_{2}\):

\ [
\ Delta U=-k\ int_ {t_ {1}} ^ {t_ {2}}\ izquierda (T-T_ {\ infty}\ derecha)\ mathrm {d} t+w_ {\ mathrm {el}}
\]
(constante\(V\))

Todo el trabajo intermitente\(w_{\mathrm{el}}\) se realiza en este intervalo de tiempo.

La derivación de la Ec. \(7.3 .24\)es general. La ecuación se puede aplicar también a un calorímetro de camisa isotérmica en el que se está produciendo una reacción. En la sección\(11.5 .2\) se mencionará el uso de esta ecuación para una corrección de energía interna de un calorímetro de reacción con una camisa isotérmica.

El valor promedio del equivalente de energía en el rango de temperatura\(T_{1}\) a\(T_{2}\) es

\ [
\ épsilon=\ frac {\ Delta U} {T_ {2} -T_ {1}} =\ frac {-\ épsilon (k/\ épsilon)\ int_ {t_ {1}} ^ {t_ {2}}\ izquierda (T-T_ {\ infty}\ derecha)\ mathrm {d} t+w_ {\ mathrm {el}}} {T_ {2} -T_ {1}}
\]

Resolviendo para\(\epsilon\), obtenemos

\ [
\ epsilon=\ frac {w_ {\ mathrm {el}}} {\ left (T_ {2} -T_ {1}\ derecha) + (k/\ épsilon)\ int_ {t_ {1}} ^ {t_ {2}}\ izquierda (T-T_ {\ infty}\ derecha)\ mathrm {d} t}
\]

El valor de\(w_{\mathrm{el}}\) se conoce a partir de\(w_{\mathrm{el}}=I^{2} R_{\mathrm{el}} \Delta t\), donde\(\Delta t\) es el intervalo de tiempo durante el cual se cierra el circuito calentador. La integral puede evaluarse numéricamente una vez que\(T_{\infty}\) se conoce.
Para calentar a presión constante,\(\mathrm{d} H\) es igual a\(\mathrm{d} U+p \mathrm{~d} V\), y podemos escribir

\ [
\ frac {\ mathrm {d} H} {\ mathrm {~d} t} =\ frac {\ mathrm {d} U} {\ mathrm {~d} t} +p\ frac {\ mathrm {d} V} {\ mathrm {~d} t} =-k\ izquierda (T-T_ {\ mathrm {ext}}\ derecha) +\ frac ac {\ mathrm {d} w_ {\ mathrm {el}}} {\ mathrm {d} t} +\ frac {\ mathrm {d} w_ {\ mathrm {cont}}} {\ mathrm {d} t}
\]
(constante\(p\))

que es análogo a la Ec. 7.3.22. Por el procedimiento descrito anteriormente para el caso de constante\(V\), obtenemos

\ [
\ Delta h=-k\ int_ {t_ {1}} ^ {t_ {2}}\ izquierda (T-T_ {\ infty}\ derecha)\ mathrm {d} t+w_ {\ mathrm {el}}
\]
(constante\(p\))

A constante\(p\), el equivalente de energía es igual a\(C_{p}=\Delta H /\left(T_{2}-T_{1}\right)\), y la expresión final para\(\epsilon\) es la misma que la dada por la Ec. 7.3.26.

Para obtener valores de\(k / \epsilon\) y\(T_{\infty}\) para su uso en la Ec. 7.3.26, necesitamos las pendientes de la curva de calentamiento en intervalos de tiempo (periodos de calificación) justo antes\(t_{1}\) y justo después\(t_{2}\). Consideremos el caso del volumen constante. En estos intervalos,\(\mathrm{d} w_{\mathrm{el}} / \mathrm{d} t\) es cero e\(\mathrm{d} U / \mathrm{d} t\) igual\(-k\left(T-T_{\infty}\right)\) (a partir de la Ec. 7.3.23). La capacidad calorífica a volumen constante es\(C_{V}=\mathrm{d} U / \mathrm{d} T\). La pendiente\(r\) en general viene dada entonces por

\ [
r=\ frac {\ mathrm {d} T} {\ mathrm {~d} t} =\ frac {\ mathrm {d} T} {\ mathrm {~d} U}\ frac {\ mathrm {d} U} {\ mathrm {~d} t} =- (k/\ épsilon)\ izquierda (T-T_ {\ infty} derecha)
\]

Aplicando esta relación a los puntos a veces\(t_{1}\) y\(t_{2}\), tenemos las siguientes ecuaciones simultáneas en las incógnitas\(k / \epsilon\) y\(T_{\infty}\):
\ [
r_ {1} =- (k/\ épsilon)\ left (T_ {1} -T_ {\ infty}\ right)\ quad r_ {2} =- (k/\ épsilon)\ left (T_ {2} -T_ {\ infty} derecha\)
\]
Las soluciones son
\ [
(k/\ epsilon) =\ frac {r_ {1} -r_ {2}} {T_ {2} -T_ {1}}\ quad T_ {\ infty} =\ frac {r_ {1} T_ {2} -r_ {2} T_ {1}} {r_ {1} -r_ {2}
\]
Finalmente,\(k\) viene dada por
\ [
k =( k/\ epsilon) \ epsilon=\ left (\ frac {r_ {1} -r_ {2}} {T_ {2} -T_ {1}}\ right)\ epsilon
\]
Cuando la presión es constante, este procedimiento produce las mismas relaciones para\(k / \epsilon, T_{\infty}\), y\(k .\)

Calorímetros de flujo continuo

Un calorímetro de flujo es un tercer tipo de calorímetro utilizado para medir la capacidad calorífica de una fase fluida. El gas o líquido fluye a través de un tubo a una tasa constante conocida más allá de un calentador eléctrico de entrada de energía constante conocida. Después de que se haya logrado un estado estacionario en el tubo, se mide el aumento de temperatura\(\Del T\) en el calentador.

Si\(\dw\el/\dt\) es la velocidad a la que se realiza el trabajo eléctrico (la energía eléctrica) y\(\dif m/\dt\) es el caudal másico, entonces en intervalo\(w=(\dw\el/\dt)\Del t\) de tiempo se realiza\(\Del t\) una cantidad de trabajo sobre una cantidad\(n=(\dif m/\dt)\Del t/M\) del fluido (donde\(M\) está la masa molar). Si el flujo de calor es insignificante, la capacidad calorífica molar de la sustancia viene dada por\ begin {ecuación}\ Cpm =\ frac {w} {n\ Del T} =\ frac {M (\ dw\ el/\ dt)} {\ Del T (\ dif m/\ dt)}\ tag {7.3.33}\ end {ecuación} Para corregir los efectos del flujo de calor, generalmente\(\Del T\) se mide sobre un rango de caudales y los resultados extrapolado a caudal infinito.

7.3.3 Valores típicos

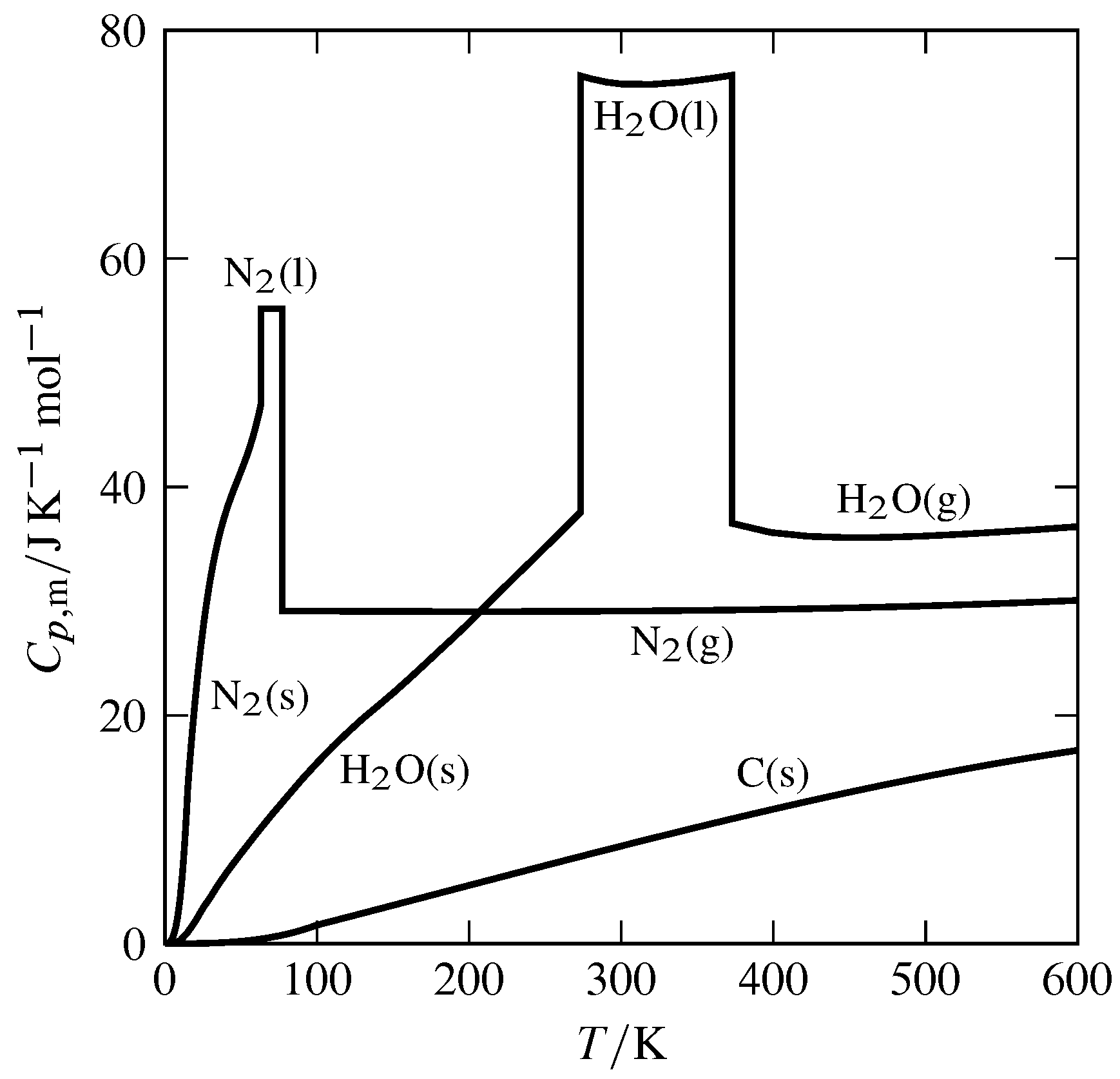
Figura 7.5 Dependencia de la temperatura de la capacidad calorífica molar a presión constante (\(p=1\br\)) de H\(_2\) O\(_2\), N y C (grafito).

La Figura 7.5 muestra la dependencia de la temperatura\(\Cpm\) de varias sustancias. Las discontinuidades observadas a ciertas temperaturas ocurren en las transiciones de fase de equilibrio. A estas temperaturas la capacidad calorífica es en efecto infinita, ya que la transición de fase de una sustancia pura implica calor finito con cambio de temperatura cero.