3.7: El Momentum Promedio de una Partícula en una Caja es Cero
- Page ID
- 79937
- Calcular el valor de expectativa para una medición
- Aplicar el concepto de valor de expectativa para calcular las propiedades promedio de un participio en un modelo de caja
- Comprender el origen de una energía de punto cero/movimiento de punto cero.
- Extender el concepto de ortogonalidad de vectores a funciones matemáticas (y funciones de onda).
Ahora que tenemos expresiones matemáticas para las funciones de onda y energías para la partícula en una caja, podemos responder a una serie de preguntas interesantes. Las respuestas a estas preguntas utilizan la mecánica cuántica para predecir algunas propiedades importantes y generales de electrones, átomos, moléculas, gases, líquidos y sólidos. La clave para abordar estas preguntas es la formulación y uso de valores de expectativa. Esto se demuestra a continuación y se utiliza en el contexto de evaluar las propiedades promedio (momentum de la partícula en una caja para el caso siguiente).
Valores clásicos de expectativa
El valor de expectativa es el valor probabilístico esperado del resultado (medición) de un experimento. No es el valor más probable de una medición; de hecho, el valor de expectativa puede incluso tener cero probabilidad de ocurrir. El valor esperado (o expectativa, expectativa matemática, media o primer momento) se refiere al valor de una variable que uno “esperaría” encontrar si se pudiera repetir el proceso de la variable aleatoria un número infinito de veces y tomar el promedio de los valores obtenidos. De manera más formal, el valor esperado es un promedio ponderado de todos los valores posibles.
Un ejemplo clásico es calcular el valor esperado (es decir, el promedio) de las calificaciones del examen en la clase. Por ejemplo, si los puntajes de clase para un examen fueron
| 65 | 67 | 94 | 43 | 67 | 76 | 94 | 67 |
La forma discreta es resumir todos los puntajes y dividirlos por el número de alumnos:
\[\langle s \rangle = \dfrac{\displaystyle \sum_i^N s(i)}{N} \label{Cl1} \]
cuál de este ejemplo de puntajes es
\[ \begin{align*} \langle s \rangle &= \dfrac{65 + 67 +94 +43 +67+76+94+76}{8} \\[4pt] &= 71.625 \end{align*} \nonumber \]
Observe que el promedio no es una puntuación permisible en un examen individual. La ecuación se\(\ref{Cl1}\) puede reescribir con “probabilidad” o “pesos de probabilidad”
\[\langle s \rangle = \sum_i^N s(i) P_s(i) \label{Cl2} \]
donde\(P_s(i)\) está la probabilidad de observar una puntuación de\(s\). Esto es solo el número de veces que ocurre en un conjunto de datos dividido por el número de elementos en ese conjunto de datos. Aplicando la Ecuación\ ref {Cl2} al conjunto de puntuaciones, necesitamos calcular estos pesos:
| Score | 65 | 67 | 94 | 43 | 76 |
|---|---|---|---|---|---|
| \(P_s\) | 1/8 | 3/8 | 2/8 | 1/8 | 1/8 |
Al igual que con todas las probabilidades, la suma de todas las probabilidades posibles debe ser una. Estos confirman que para los pesos aquí:
\[ \dfrac{1}{8} + \dfrac{3}{8} + \dfrac{2}{8} + \dfrac{1}{8} + \dfrac{1}{8} = \dfrac{8}{8} =1 \nonumber \]
Este es el criterio discretizado de “normalización” (lo mismo que por qué normalizamos las funciones de onda).
Entonces, ahora podemos usar Ecuación\(\ref{Cl2}\) correctamente
\[ \begin{align*} \langle s \rangle &= 65 \times \dfrac{1}{8} + 67\times \dfrac{3}{8} +94\times \dfrac{2}{8} + 43 \times\dfrac{1}{8} +76\times \dfrac{1}{8} \\[4pt] &= 71.625 \end{align*} \nonumber \]
De ahí que la Ecuación\(\ref{Cl2}\) dé el mismo resultado, como se esperaba, de la Ecuación\(\ref{Cl1}\).
Valores de expectativa cuántica
La extensión del enfoque de expectativa clásica (promedio) en el Ejemplo 3.7.1 usando la ecuación\ ref {Cl2} para evaluar los valores de expectativa mecánica cuántica requiere tres pequeños cambios:
- Cambiar de variables descretizadas a variables continuas
- Sustituir la función de onda al cuadrado por los pesos de probabilidad (es decir, la distribución de probabilidad)
- Usar un operador en lugar del escalar
De ahí que el valor de expectativa mecánica cuántica\(\langle o \rangle\) para un observable\(o\),, asociado a un operador,\(\hat{O}\), viene dado por
\[ \langle o \rangle = \int _{-\infty}^{+\infty} \psi^* \hat{O} \psi \, dx \label{expect} \]
donde\(x\) está el rango de espacio sobre el que se integra (es decir, una integración sobre todas las probabilidades posibles). El valor de expectativa cambia a medida que cambia la función de onda y el operador utilizado (es decir, qué observable está promediando).
En general, cambiar la función de onda cambia el valor de expectativa para ese operador para un estado definido por esa función de onda.
Energía promedio de una partícula en una caja
Si generalizamos esta conclusión, tales integrales dan el valor promedio para cualquier cantidad física mediante el uso del operador correspondiente a ese físico observable en la integral en la Ecuación\(\ref{expect}\). En la siguiente ecuación, el símbolo\(\left \langle H \right \rangle\) se utiliza para denotar el valor promedio de la energía total.
\[ \begin{align} \left \langle H \right \rangle &= \int \limits ^{\infty}_{-\infty} \psi ^* (x) \hat {H} \psi (x) dx \\[4pt] &= \int \limits ^{\infty}_{-\infty} \psi ^* (x) \hat {KE} \psi (x) dx + \int \limits ^{\infty}_{-\infty} \psi ^* (x) \hat {V} \psi (x) dx \\[4pt] &= \underset{\text {average kinetic energy} }{ \int \limits ^{\infty}_{-\infty} \psi ^* (x) \left ( \frac {-\hbar ^2}{2m} \right ) \frac {\partial ^2 }{ \partial x^2} \psi (x) dx} + \underset{ \text {average potential energy} }{\int \limits ^{\infty}_{-\infty} \psi ^* (x) \hat{V} (x) \psi (x) dx} \label{3-35} \end{align} \]
El operador hamiltoniano consiste en un término de energía cinética y un término de energía potencial. El operador de energía cinética implica la diferenciación de la función de onda a la derecha de la misma. Este paso debe completarse antes de multiplicarse por el complejo conjugado de la función de onda. La energía potencial, sin embargo, generalmente depende solo de la posición y no del impulso (es decir, involucra fuerzas conservadoras). El operador de energía potencial, por lo tanto, solo involucra las coordenadas de una partícula y no implica diferenciación. Por esta razón no necesitamos usar un caret over\(V\) en Ecuación\(\ref{3-35}\).
La ecuación\ ref {3-35} puede simplificarse
\[ \langle H \rangle = \langle KE \rangle + \langle V \rangle \label{3-35 braket} \]
La integral de energía potencial involucra entonces solo productos de funciones, y el orden de multiplicación no afecta el resultado, por ejemplo 6×4 = 4×6 = 24. Esta propiedad se llama propiedad conmutativa. Por lo tanto, la energía potencial promedio puede escribirse como
\[ \left \langle V \right \rangle = \int \limits ^{\infty}_{-\infty} V (x) \psi ^* (x) \psi (x) dx \label{3-36} \]
Esta integral nos está diciendo que tomemos la probabilidad de que la partícula esté en el intervalo\(dx\) at\(x\), es decir\(ψ^*(x)ψ(x)dx\), multiplicar esta probabilidad por la energía potencial en\(x\), y suma (es decir, integrar) sobre todos los valores posibles de\(x\). Este procedimiento es justamente la forma de calcular la energía potencial promedio\(\left \langle V \right \rangle\) de la partícula.
Evaluar las dos integrales en Ecuación\(\ref{3-35}\) para la función de onda PIB\(ψ(x) = \sqrt{\dfrac{2}{L}} \sin(k x)\) con la función potencial\(V(x) = 0\) de 0 a la longitud de una caja\(L\) con\(k= \dfrac{\pi }{L}\).
Solución
La energía cinética promedio es
\[\begin{align*} \langle KE \rangle &= \int \limits ^{L}_{0} \left(\sqrt{\dfrac{2}{L}}\right) \sin(kx) \left ( \frac {-\hbar ^2}{2m} \right ) \frac {\partial ^2 }{ \partial x^2} \left(\sqrt{\dfrac{2}{L}}\right) \sin(kx) dx \\[4pt] &= \left(\dfrac{2}{L}\right) \int \limits ^{L}_{0} \sin(kx) \left ( \frac {-\hbar ^2}{2m} \right ) \frac {\partial }{ \partial x} \cos(kx)(k) dx \\[4pt] &= \left(\dfrac{2}{L}\right) \int \limits ^{L}_{0} \sin(kx) \left ( \frac {-\hbar ^2}{2m} \right ) \sin(kx)(k)(-k) dx \\[4pt] &= \left(\dfrac{2}{L}\right) \left ( \frac { k^2 \hbar ^2}{2m} \right ) \int \limits ^{L}_{0} \sin^2(kx) dx \end{align*} \nonumber \]
Podemos resolver este intergral usando la representación estándar de medio ángulo de una tabla integral. O podemos reconocer que ya hicimos esta integral cuando normalizamos la función de onda PIB reescribiendo esta integral:
\[\begin{align*} \langle KE \rangle &= \left(\dfrac{2}{L}\right) \left ( \frac { k^2 \hbar ^2}{2m} \right ) \int \limits ^{L}_{0} \sin^2(kx) dx \\[4pt] &= \left ( \frac { k^2 \hbar ^2}{2m} \right ) \int \limits ^{L}_{0} \left(\dfrac{2}{L}\right) \sin^2(kx) dx \\[4pt] &=\left ( \frac { k^2 \hbar ^2}{2m} \right ) \cancelto{1}{\int \limits ^{L}_{0} \psi^*(x)\psi(x) dx} \\[4pt] &= \frac { k^2 \hbar ^2}{2m} \end{align*} \nonumber \]
Así, el valor promedio de la energía total de este sistema en particular es
\[ \langle KE \rangle = \dfrac { k^2 \hbar ^2}{2m} = \dfrac { \pi^2 \hbar ^2}{2mL^2} \nonumber \]
Por lo tanto, la energía cinética promedio de la función de onda depende del número\(n\) cuántico
La energía potencial promedio es
\[ \langle V \rangle = \int \limits ^{\infty}_{-\infty} \sin(kx) 0 \sin(kx) dx = 0 \nonumber \]
Así, la energía potencial promedio del PIB es 0 independientemente de la función de onda.
De ahí a través de la ecuación\ ref {3-35 braket} para este sistema y conjunto de funciones de onda
\[ \langle H \rangle = \dfrac { \pi^2 \hbar ^2}{2mL^2} \nonumber \]
Este es el mismo resultado obtenido al resolver la ecuación de valor propio para el PIB. Sin embargo, si las funciones de onda utilizadas NO fueron estados propios de la energía, entonces no podemos usar el enfoque de valor propio y necesitamos confiar en los valores de expectativa para describir la energía del sistema.
¿Cuál es la energía más baja para una partícula en una caja? El nivel de energía más bajo es\(E_1\), y es importante reconocer que esta energía más baja de una partícula en una caja no es cero. Esta energía finita se llama energía de punto cero, y el movimiento asociado con esta energía se llama movimiento de punto cero. Se dice que cualquier sistema que esté restringido a alguna región del espacio está ligado. La energía de punto cero y el movimiento son manifestaciones de las propiedades de las olas y el Principio de Incertidumbre de Heisenberg, y son propiedades generales de los sistemas mecánicos cuánticos unidos.
¿Qué sucede con el espaciado del nivel de energía para una partícula en una caja cuando\(mL^2\) se vuelve mucho más grande que\(h^2\)? ¿Qué implica este resultado sobre la relevancia de la cuantificación de energía para pelones de béisbol en una caja entre el montículo de pitcheo y el plato casero? ¿Qué implicaciones tiene la mecánica cuántica para el juego del béisbol en un mundo donde\(h\) es tan grande que las pelusas exhiben efectos cuánticos?
- Contestar
-
Como\(mL^2\) se hace mucho más grande que\(h^2\), como son los objetos cotidianos, el espaciamiento entre los niveles de energía se vuelve mucho menor. Esto muestra cómo las cuantificaciones de los niveles de energía se vuelven irrelevantes para un objeto cotidiano, ya que las cuantificaciones de la energía de las pelolas de béisbol en una caja entre el montículo de cabeceo y la placa de inicio parecerían particularmente continuas para una masa y una longitud de caja tan relativamente grandes. Si h fuera tan grande que un beisbol experimenta efectos cuánticos entonces un juego de beisbol sería mucho menos predecible, en un mundo clásico la posición de un beisbol puede predecirse fácilmente por la comprensión cotidiana del movimiento de proyectiles, sin embargo, en un mundo tan cuántico el beisbol no se comportaría con esperaba el movimiento del proyectil pero en su lugar se comportan como ondas con una probabilidad de estar en una determinada posición.
La primera derivada de una función es la tasa de cambio de la función, y la segunda derivada es la tasa de cambio en la tasa de cambio, también conocida como la curvatura. Una función con una segunda derivada grande está cambiando muy rápidamente. Dado que la segunda derivada de la función de onda ocurre en el operador hamiltoniano que se utiliza para calcular la energía mediante el uso de la ecuación de Schrödinger, una función de onda que tenga curvaturas más nítidas que otra, es decir, segundas derivadas mayores, debería corresponder a un estado que tenga una mayor energía. Una función de onda con más nodos que otra sobre la misma región del espacio debe tener curvaturas más nítidas y segundas derivadas más grandes, y por lo tanto debe corresponder a un estado de mayor energía.
Identifica una relación entre el número de nodos en una función de onda y su energía examinando las gráficas que realizó anteriormente. Un nodo es el punto donde la amplitud pasa por cero. ¿Qué significa la presencia de muchos nodos sobre la forma de la función de onda?
Posición promedio de una partícula en una caja
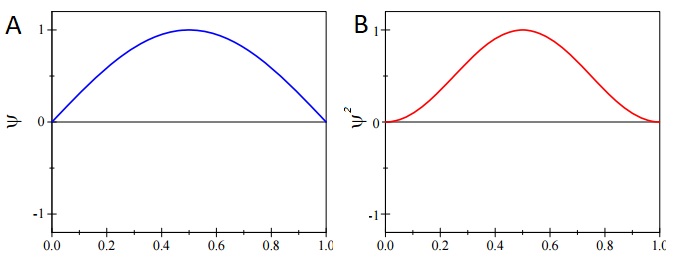
Podemos calcular la posición más probable de la partícula a partir del conocimiento de la distribución de probabilidad,\(ψ^* ψ\). Para la partícula de estado fundamental en una caja de ondafunción con\(n=1\) (Figura\(\PageIndex{1a}\))
\[\psi_{n=1} = \sqrt{\dfrac{2}{L}} \sin \left(\dfrac{\pi x}{L} \right) \label{PIB} \]
Este estado tiene la siguiente distribución de probabilidad (Figura\(\PageIndex{1b}\)):
\[\psi^*_{n=1} \psi_{n=1} = \dfrac{2}{L} \sin^2 \left(\dfrac{\pi x}{L} \right) \nonumber \]
El valor de expectativa para la posición con la\(\hat{x} = x\) operación para cualquier función de onda (Ecuación\(\ref{expect}\)) es
\[ \langle x \rangle = \int _{-\infty}^{+\infty} \psi^* x \psi \, dx \nonumber \]
que para la función de onda de estado fundamental (Ecuación\(\ref{PIB}\)) mostrada en la Figura 3.7.1 es
\[ \begin{align} \langle x \rangle &= \int _{-\infty}^{+\infty} \sqrt{\dfrac{2}{L}} \sin \left(\dfrac{\pi x}{L} \right) x \sqrt{\dfrac{2}{L}} \sin \left(\dfrac{\pi x}{L} \right) \, dx \\[4pt] &= \dfrac{2}{L} \int _{-\infty}^{+\infty} x \sin^2 \left(\dfrac{\pi x}{L} \right) \label{GSExpect} \end{align} \]
Sin siquiera tener que evaluar la Ecuación\(\ref{GSExpect}\), podemos obtener el valor de expectativa simplemente inspeccionando\( \psi^*_{n=1} \psi_{n=1}\) en (Figura\(\PageIndex{1; right}\)). Esta es una distribución simétrica alrededor del centro de la caja (\(L/2\)) por lo que es igual de probable que se encuentre en la mitad izquierda que en la mitad derecha. Además, específicamente en cualquier punto una distancia fija de la media, i.e.
\[\psi^*_{n=1} \psi_{n=1} (L/2 + \Delta x) = \psi^*_{n=1} \psi_{n=1} (L/2 - \Delta x) \nonumber \]
Por lo tanto, es más probable que la partícula se encuentre en el centro de la caja. Entonces
\[ \langle x \rangle = \dfrac{L}{2} \nonumber \]
Utilice la forma general de la función de onda partícula-en-a-caja para\(n\) que cualquiera encuentre la expresión matemática para el valor de expectativa de posición\(\left \langle x \right \rangle\) para una caja de longitud L. ¿Cómo\(\left \langle x \right \rangle\) depende de\(n\)?
Momentum promedio de una partícula en una caja
¿Cuál es el impulso promedio de una partícula en la caja? Comenzamos con Ecuación\(\ref{expect}\) y usamos el operador de momentum
\[\hat{p}_{x}=-i\hbar\dfrac{\partial}{\partial x}\label{3.2.3a} \]
Observamos que las funciones de onda particle-in-a-box no son funciones propias del operador momentum (Ejercicio 3.7.4 ). Sin embargo, esto no significa que Ecuación\(\ref{expect}\) sea inaplicable como lo demuestra el Ejemplo 3.7.2 .
A pesar de que las funciones de onda no son funciones propias de impulso, podemos calcular el valor de expectativa para el impulso. Mostrar que la expectativa o valor promedio para el impulso de un electrón en la caja es cero en cada estado (es decir, valores arbitrarios de\(n\)).
Estrategia
Primero escriba la integral del valor de expectativa (Ecuación\(\ref{expect}\)) con el operador de impulso. Luego inserte la expresión para la función de onda y evalúe la integral como se muestra aquí.
Contestar
\[\begin{align*} \left \langle p \right \rangle &= \int \limits ^L_0 \psi ^*_n (x) \left ( -i\hbar \dfrac {d}{dx} \right ) \psi _n (x) dx \\[4pt] &= \int \limits ^L_0 \left (\dfrac {2}{L} \right )^{1/2} \sin \left(\dfrac {n \pi x}{L}\right) \left ( -i\hbar \dfrac {d}{dx} \right ) \left (\dfrac {2}{L} \right )^{1/2} \sin \left(\dfrac {n \pi x }{L} \right) dx \\[4pt] &= -i \hbar \left (\dfrac {2}{L} \right ) \int \limits ^L_0 \sin \left(\dfrac {n \pi x}{L}\right) \left ( \dfrac {d}{dx} \right ) \sin \left(\dfrac {n \pi x}{L}\right) dx \\[4pt] &= -i \hbar \left (\dfrac {2}{L} \right ) \left ( \dfrac {n \pi}{L} \right ) \int \limits ^L_0 \sin \left(\dfrac {n \pi x}{L} \right) \cos \left(\dfrac {n \pi x}{L}\right) dx \\[4pt] &= 0 \end{align*} \nonumber \]
Tenga en cuenta que esto tiene sentido ya que las partículas pasan la misma cantidad de tiempo viajando en la\(–x\) dirección\(+x\) y.
Interpretación
Puede parecer que esto quiere decir que la partícula en una caja no tiene ningún impulso, lo cual es incorrecto porque sabemos que la energía nunca es cero. De hecho, la energía que obtuvimos para la partícula en una caja es completamente energía cinética porque establecemos la energía potencial en 0. Dado que la energía cinética es el impulso al cuadrado dividido por el doble de la masa, es fácil entender cómo el impulso promedio puede ser cero y la energía cinética finita
Mostrar que las funciones de onda de partículas en una caja no son funciones propias del operador de impulso (Ecuación\(\ref{3.2.3a}\)).
- Contestar
-
La forma más fácil de abordar esta pregunta es preguntar si la función de onda PIB también satisface la ecuación de valor propio usando la operación de impulso en lugar del operador hamiltoniano (3er postulado de QM). Eso es
\[\hat{p}_x \psi(n) = p \psi(n) \nonumber \]
con las siguientes funciones de onda PIB
\[\psi_{n}=\sqrt{\dfrac{2}{L}} \sin \left(\dfrac{n \pi x}{L}\right) \nonumber \]
y
\[\hat{p}=- i\hbar \dfrac{d}{d x } \nonumber \]
y\(p\) es un escalar real (ya que es un medible).
\[ \begin{align*} \hat{p}_x \psi_{n} &= - i\hbar \dfrac{d}{d x} \left[\sqrt{\dfrac{2}{L}} \sin \left(\dfrac{n \pi x}{L}\right)\right] \\[4pt] &= -i \hbar \sqrt{ \dfrac{2}{L}} \cos \left(\dfrac{n \pi x}{L}\right) \left(\dfrac{n \pi}{L}\right) \\[4pt] &\neq p \psi_{n} \end{align*} \nonumber \]
Por lo tanto, las funciones de onda PIB NO son funciones propias del operador de impulso.
Debe ser igualmente probable que la partícula en una caja tenga un impulso\(-p\) como\(+p\). El promedio de\(+p\) y\(–p\) es cero, sin embargo\(p^2\) y el promedio de no\(p^2\) son cero. La información de que es igualmente probable que la partícula tenga un impulso\(+p\) o\(–p\) esté contenida en la función de onda. De hecho, la función seno es una representación de las dos funciones propias de impulso\(e^{+ikx}\) y\(e^{-ikx}\) (Figura 3.7.2 ).
Escriba la función de onda de partícula en una caja como una combinación lineal normalizada de las funciones propias del momento\(e^{ikx}\) y\(e^{-ikx}\) usando la fórmula de Euler. Demostrar que los valores propios de impulso para estas dos funciones son\(p = +ħk\) y\(-ħk\).
La interpretación de los resultados del Ejercicio 3.7.6 es físicamente interesante. Las funciones de onda exponenciales en la combinación lineal para la función sinusoidal representan las dos direcciones opuestas en las que el electrón puede moverse. Un término exponencial representa movimiento hacia la izquierda y el otro término representa movimiento a la derecha (Figura 3.7.2 ).
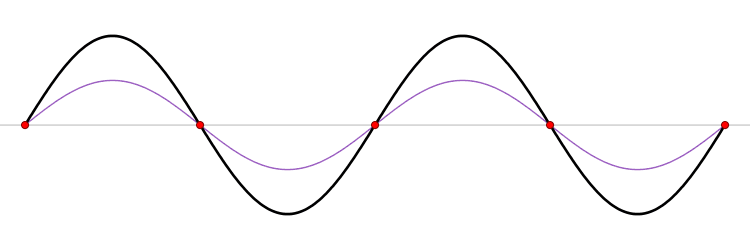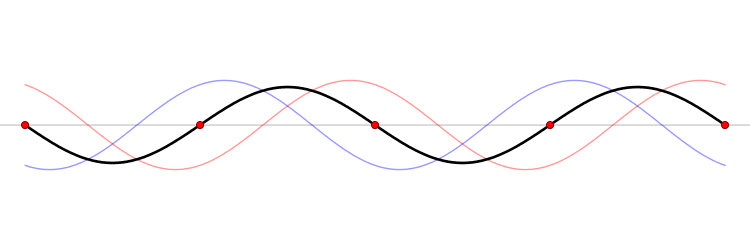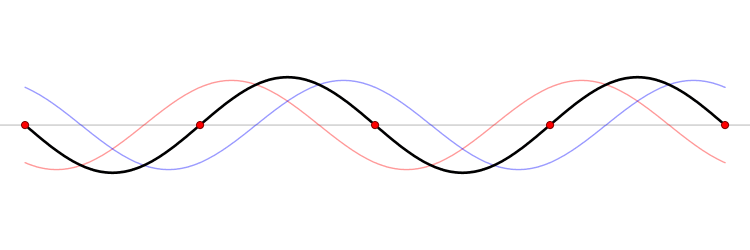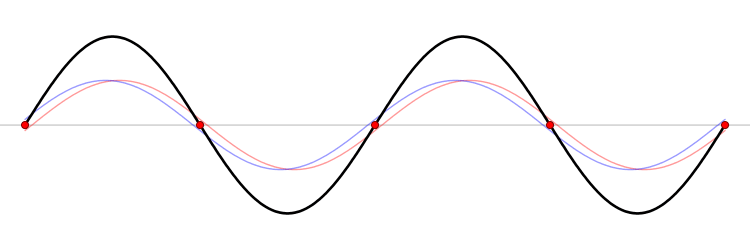
Los electrones se están moviendo, tienen energía cinética e impulso, sin embargo el impulso promedio es cero.
¿El hecho de que el impulso promedio de un electrón sea cero y la posición promedio sea\(L/2\) viola el Principio de Incertidumbre de Heisenberg? No, porque el Principio de Incertidumbre de Heisenberg se refiere a la incertidumbre en el impulso y en la posición, no a los valores promedio. Se pueden obtener valores cuantitativos para estas incertidumbres para comparar con el límite establecido por el Principio de Incertidumbre de Heisenberg para el producto de las incertidumbres en el impulso y la posición. No obstante, para ello necesitamos una definición cuantitativa de incertidumbre, la cual se discute en la siguiente Sección.
Ortogonalidad
En el cálculo vectorial, la ortogonalidad es la relación de dos líneas en ángulo recto entre sí (es decir, perpendicularidad), pero se generaliza en\(n\) dimensiones a través de "productos de punto" o "productos internos” de amplitud cero. Por lo tanto, se piensa que la ortogonalidad describe objetos no superpuestos, no correlacionados o independientes de algún tipo. El concepto de ortogonalidad se extiende también a las funciones (funciones de onda o de otro tipo). Dos funciones\(\psi_A\) y\(\psi_B\) se dice que son ortogonales si
\[ \int \limits _{all space} \psi _A^* \psi _B d\tau = 0 \label{3.7.3} \]
En general, las funciones propias de un operador mecánico cuántico con diferentes valores propios son ortogonales. ¿Las funciones propias de la partícula en una caja son ortogonales hamiltonianas?
Evaluar la integral\(\int \psi ^*_1 \psi _3 dx\) para todos los pares posibles de funciones propias de partículas en una caja desde\(n=1\) hasta\(n=3\) (usar argumentos de simetría siempre que sea posible) y explicar lo que dicen los resultados sobre la ortogonalidad de las funciones.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski


Solución alternativa
Una alternativa, aunque más complicada, es reconocer que la incertidumbre de\(p\) debe ser cero si la función de onda es un estado propio del operador de impulso. De ahí
\[\sqrt{\langle p^{2}\rangle - \langle p \rangle ^{2}}=0 \nonumber \]
Esto requiere calcular los valores\(\langle p^{2}\rangle\) y\(\langle p \rangle\) expectativas:
\[\begin{align*} \langle p \rangle &=\int_{0}^{L} \psi^{*}\left[-i \hbar \dfrac{d}{d x}\right] \psi d x \\[4pt] &=-i \hbar \int_{0}^{L} \dfrac{2}{L} \sin \left(\dfrac{n \pi x}{L}\right) \dfrac{d}{dx} x \sin \left(\dfrac{n \pi x}{L}\right) dx \\[4pt] &=-i \dfrac{\mathrm{h}^2}{L} \int_{0}^{L} \sin \left(\dfrac{n \pi x}{L}\right) \cos \left(\dfrac{n \pi x}{L}\right) dx \\[4pt] &= 0 \end{align*} \nonumber \]
Esta integral es cero a través de la ortonormalidad de las funciones seno y coseno (aunque se puede expandir el integrando y confirmarlo).
\[ \begin{align*} \langle p^{2} \rangle &=\int_{0}^{L} \psi^{*} \left[-i \hbar \dfrac{d}{d x}\right]^{2} \psi d x \\[4pt] &=\dfrac{\mathrm{h}^2}{L} \int_{0}^{L} \sin \left(\dfrac{n \pi x}{L}\right) \dfrac{d^{2} }{d x^{2}} \sin \left(\dfrac{n \pi x}{L}\right) d x \\[4pt] &=\dfrac{-\mathrm{h}^2}{L} \int_{0}^{L} \sin \left(\dfrac{n \pi x}{L}\right) \sin \left(\dfrac{n \pi x}{L}\right) d x \\[4pt] &= -\dfrac{\mathrm{h}^2}{L} \end{align*} \nonumber \]
Ahora la integral anterior es 1 usando ortonormalidad (aunque puedes expandir el integrando y confirmarlo). Ahora calculamos la incertidumbre en el impulso en las funciones de onda del PIB:
\[ \begin{align*} \sqrt{\langle p^{2} \rangle - \langle p \rangle^2} &=\sqrt{\dfrac{-\mathrm{h}^2}{L} -0^{2}} \\[4pt] &= \sqrt{\dfrac{-\mathrm{h}^2}{L}} \\[4pt] &\neq 0 \rightarrow \end{align*} \nonumber \]
Dado que la incertidumbre no es 0, diferentes mediciones (experimentos) darán como resultado que se cuantifiquen diferentes valores de impulso. Por lo tanto, las funciones de onda PIB no son funciones propias del operador de impulso.