4.3: Las cantidades observables deben ser valores propios de los operadores mecánicos cuánticos
- Page ID
- 79292
- Introducir al papel de las ecuaciones de valores propios en la obtención de observables a partir de un sistema
- Entender cómo se calculan los valores de expectativa si las funciones de onda no son un estado propio del operador para lo observable.
Recordemos, que podemos identificar al operador de energía total, que se llama operador hamiltoniano,\(\hat{H}\), como que consiste en el operador de energía cinética más el operador de energía potencial.
\[\hat {H} = - \dfrac {\hbar ^2}{2m} \nabla ^2 + \hat {V} (x, y , z ) \label{3-22} \]
Usando esta notación, escribimos la ecuación de Schrödinger como
\[ \hat {H} | \psi (x , y , z ) \rangle = E | \psi ( x , y , z ) \rangle \label{3-23} \]
La ecuación\(\ref{3-23}\) dice que el operador hamiltoniano opera sobre la función de onda para producir la energía, que es un número, (una cantidad de julios), multiplicado por la función de onda. Tal ecuación, donde el operador, operando sobre una función, produce una constante multiplicada por la función, se denomina ecuación de valor propio. La función se llama función propia, y el valor numérico resultante se llama el valor propio. Eigen aquí está la palabra alemana que significa yo o propio.
Es un principio general de la Mecánica Cuántica que hay un operador para cada físico observable. Un físico observable es cualquier cosa que se pueda medir. Si la función de onda que describe un sistema es una función propia de un operador, entonces el valor del observable asociado se extrae de la función propia operando en la función propia con el operador apropiado. El valor de lo observable para el sistema es el valor propio, y se dice que el sistema está en un estado propio. Ecuación\(\ref{3-23}\) establece este principio matemáticamente para el caso de la energía como lo observable.
Si un sistema es descrito por la función propia\(\Psi\) de un operador\(\hat{A}\) entonces el valor medido para la propiedad observable correspondiente a siempre\(\hat{A}\) será el valor propio\(a\), que se puede calcular a partir de la ecuación de valor propio.
\[ \hat {A} | \Psi \rangle = a | \Psi \rangle \label {4.3.1} \]
Considera un operador general de espacio real\(A(x)\). Cuando este operador actúa sobre una función de onda general,\(\psi(x)\) el resultado suele ser una función de onda con una forma completamente diferente. Sin embargo, hay ciertas funciones de onda especiales que son tales que cuando\(A\) actúa sobre ellas el resultado es solo un múltiplo de la función de onda original. Estas funciones de onda especiales se llaman estados propios, y los múltiplos se llaman valores propios. Por lo tanto, si
\[A | \psi_a(x) \rangle = a | \psi_a(x) \rangle \label{4.3.2} \]
donde\(a\) es un número complejo, entonces\(\psi_a\) se llama un estado propio de\(A\) correspondiente al valor propio\(a\).
Supongamos que\(A\) es un operador correspondiente a alguna variable dinámica física. Considera una partícula cuya función de onda es\(\psi_a\). La expectativa de valor\(A\) en este estado es simplemente
\[ \begin{align*} \langle A\rangle &= \int_{-\infty}^\infty \psi_a^{\ast} A \psi_a dx \\[4pt] &= a \int_{-\infty}^\infty \psi_a^{\ast} \psi_a dx \\[4pt] &= a. \end{align*} \nonumber \]
donde se ha hecho uso de la Ecuación\(\ref{4.3.2}\) y la condición de normalización. Por otra parte,
\[ \begin{align*} \langle A^2\rangle &= \int_{-\infty}^\infty \psi_a^{\ast} A^2 \psi_a dx \\[4pt] &= a \int_{-\infty}^\infty \psi_a^{\ast} A \psi_a dx \\[4pt] &= a^2 \int_{-\infty}^\infty \psi_a^{\ast} \psi_a dx \\[4pt] &= a^2. \end{align*} \nonumber \]
Entonces la varianza de\(A\) es
\[ \begin{align*} \sigma_A^{ 2} &= \langle A^2\rangle - \langle A\rangle^2 = a^2-a^2 \\[4pt] &= 0. \end{align*} \nonumber \]
El hecho de que la varianza sea cero implica que cada medición de\(A\) está obligada a producir el mismo resultado: a saber,\(a\). Así, el estado propio\(\psi_a\) es un estado que está asociado con un valor único de la variable dinámica correspondiente a\(A\). Este valor único es simplemente el valor propio asociado determinado por la ecuación\(\ref{4.3.2}\).
Valores de Expectativa
Hemos visto que\(\vert\psi(x,t)\vert^{ 2}\) es la densidad de probabilidad de una medición del desplazamiento de una partícula que produce el valor\(x\) en el tiempo\(t\). Supongamos que hicimos un gran número de mediciones independientes del desplazamiento en un número igualmente grande de sistemas cuánticos idénticos. En general, las mediciones realizadas en diferentes sistemas producirán diferentes resultados. Sin embargo, a partir de la definición de probabilidad, la media de todos estos resultados es simplemente
\[ \langle x\rangle = \int_{-\infty}^{\infty} x \vert\psi\vert^{ 2} dx \label{ 4.3.5} \]
Aquí,\(\langle x\rangle\) se llama el valor de expectativa de\(x\). Del mismo modo el valor de expectativa de cualquier función de\(x\) es
\[ \langle f(x)\rangle = \int_{-\infty}^{\infty} f(x) \vert\psi\vert^{ 2} dx.\label{ 4.3.6} \]
El valor promedio de una medición observable de un estado en función de onda (normalizada)\(\psi\) con operador\(\hat{A}\) viene dado por el valor de expectativa\(\langle a \rangle\):
\[ \begin{align} \langle a \rangle &= \langle \psi | a |\psi \rangle \\[4pt] &= \int_{-\infty}^{\infty} \psi^* \hat{A} \psi dx \label{4.3.7} \end{align} \]
Si se usó una función de onda no normalizada, entonces la ecuación\(\ref{4.3.7}\) cambia a
\[ \begin{align} \langle a \rangle &= \dfrac{\langle \psi | a |\psi \rangle}{\langle \psi | \psi \rangle} \\[4pt] &=\dfrac{ \displaystyle \int_{-\infty}^{\infty} \psi^* \hat{A} \psi dx}{ \displaystyle \int_{-\infty}^{\infty} \psi^* \psi dx} \label{4.3.8} \end{align} \]
El denominador es solo el requisito de normalización discutido anteriormente. En general, los resultados de las distintas mediciones de\(x\) serán dispersos alrededor del valor de expectativa\(\langle x\rangle\). El grado de dispersión se parametriza por la cantidad
\[ \begin{align} \sigma^2_x &= \int_{-\infty}^{\infty} \left(x-\langle x\rangle \right)^2 |\psi|^{ 2} dx \\[4pt] &\equiv \langle x^2\rangle -\langle x\rangle^{2}, \label{4.3.9} \end{align} \]
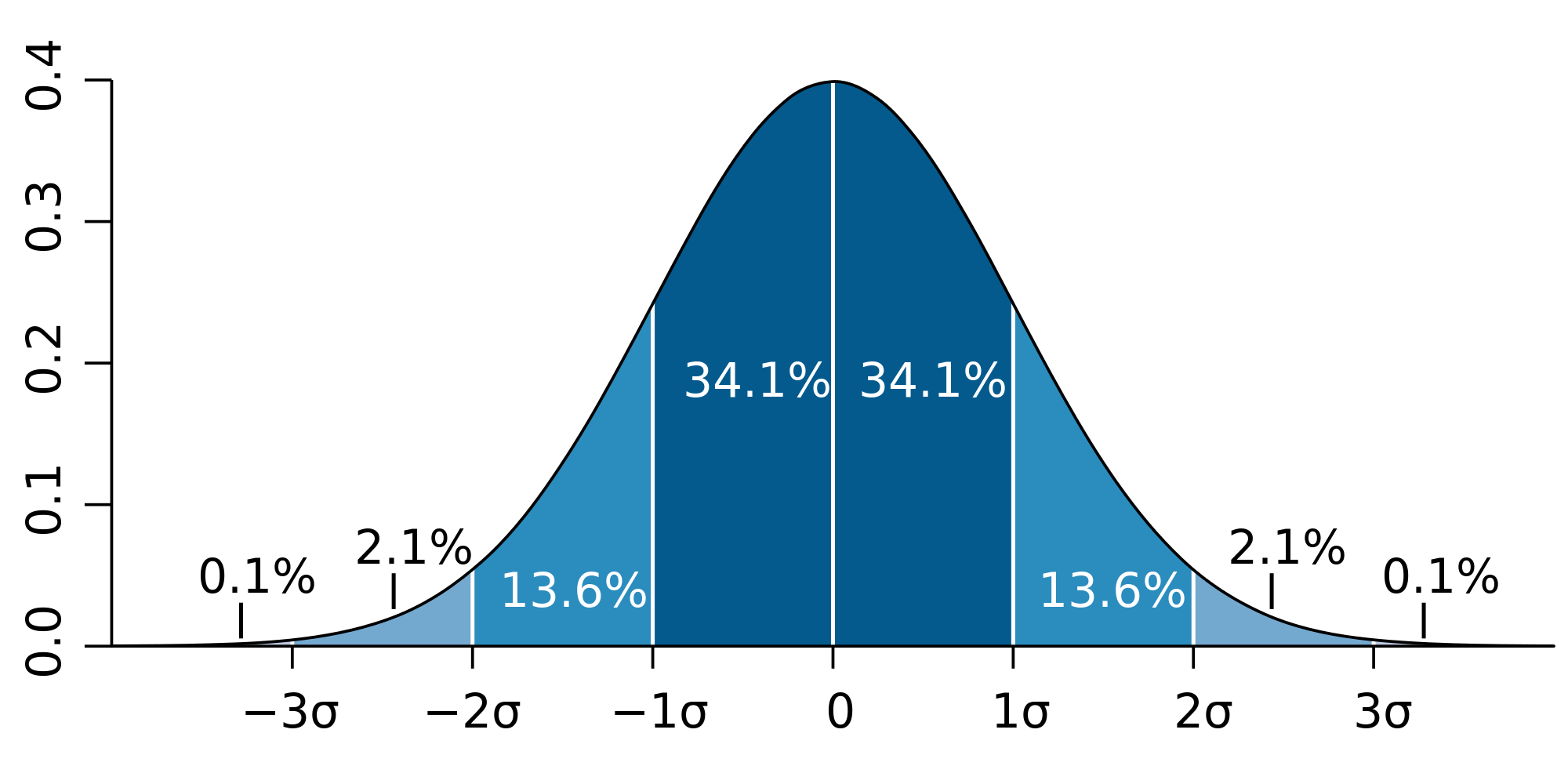
que se conoce como la varianza de\(x\). La raíz cuadrada de esta cantidad,\(\sigma_x\), se llama la desviación estándar de\(x\). Por lo general, esperamos que los resultados de\(x\) las mediciones de se encuentren dentro de algunas desviaciones estándar del valor de expectativa (Figura 4.3.1 ).
Para una partícula en una caja en su estado fundamental, calcule el valor de expectativa del
- posición,
- el momento lineal,
- la energía cinética, y
- la energía total
Solución
Primero se necesita definir la función de onda. A partir de las soluciones de partículas en la caja, la función de onda del estado fundamental (\(n=1\)es
\[\psi = \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac{\pi x}{L} \right ) \nonumber \]
Podemos confirmar que la función de onda está normalizada.
\[\int \psi^* \psi \, d\tau = \int_{0}^{L} \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac{\pi x}{L} \right ) \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac{\pi x}{L} \right ) \, dx = 1 \nonumber \]
De ahí que la Ecuación\(\ref{4.3.7}\) sea la ecuación relevante a utilizar.
El valor de expectativa de la posición es:
\[ \begin{align*} \left \langle x \right \rangle &= \int \psi^* x \psi \, d\tau = \int_{0}^{L} \sqrt{\dfrac{2}{L}} x \sin \left ( \dfrac{\pi x}{L} \right ) \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac{\pi x}{L} \right ) \, dx \\[4pt] &=\dfrac{2}{L} \int_{0}^{L} x \sin^2 \left ( \dfrac{\pi x}{L} \right ) \, dx \\[4pt] &= \dfrac{L}{2} \end{align*} \nonumber \]
El valor de expectativa del impulso es:
\[ \begin{align*} \left \langle p \right \rangle &= \int \psi^* \hat{p} \psi \, d\tau =\int_{0}^{L} \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac{\pi x}{L} \right ) \left ( -i\hbar \dfrac{d}{dx} \right ) \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac{\pi x}{L} \right ) \, dx \\[4pt] &= \dfrac{2i\hbar\pi}{L^2} \int_{0}^{L} \sin \left ( \dfrac{\pi x}{L} \right ) \cos \left ( \dfrac{\pi x}{L} \right ) \, dx \\[4pt] &= 0 \end{align*} \nonumber \]
El valor de expectativa de la energía cinética es:
\[ \begin{align*} \left \langle T \right \rangle &= \int \psi^* \hat{K} \psi \, d\tau = \dfrac{2}{L} \int_{0}^{L} \sin \left ( \dfrac{\pi x}{L} \right ) \left ( -\dfrac{\hbar^2}{2m} \dfrac{\partial^2}{\partial x^2} \right ) \sin \left ( \dfrac{\pi x}{L} \right ) \, dx \\[4pt] &= \dfrac{\hbar^2 \pi^2}{2mL^2} \dfrac{2}{L} \int_{0}^{L} \sin^2 \left ( \dfrac{\pi x}{L} \right ) \, dx \\[4pt] &= \dfrac{\hbar^2 \pi^2}{2mL^2} \end{align*} \nonumber \]
Una posición “en promedio” se encuentra en el medio de la caja (\(L/2\)). Tiene igual probabilidad de viajar hacia la izquierda o hacia la derecha, por lo que el impulso promedio y la velocidad deben ser cero. La energía cinética promedio debe ser igual a la energía total del estado fundamental de la partícula en la caja, ya que no hay otro componente energético (es decir,\(V=0\)).
Expandiendo la función de onda
También es posible demostrar que los estados propios de un operador atribuidos a un observable forman un conjunto completo (es decir, que cualquier función de onda general puede escribirse como una combinación lineal de estos autoestados). No obstante, la prueba es bastante difícil, y aquí no la intentaremos.
En resumen, dado un operador\(\hat{A}\), cualquier función de onda general,\(\psi(x)\), se puede escribir
\[\psi = \sum_{i}c_i \phi_i\label{4.3.9A} \]
donde\(c_i\) son pesos complejos, y los\(\phi(x)\) son los autoestados normalizados (y mutuamente ortogonales) de\(\hat{A}\): es decir,
\[A \phi_i = a_i \phi_i \label{4.3.10} \]
donde\(a_i\) es el valor propio correspondiente al estado propio\(\phi_i\), y
\[\int_{-\infty}^\infty \phi_i^\ast \phi_j dx = \delta_{ij}. \label{4.3.11} \]
Aquí,\(\delta_{ij}\) se llama la función delta de Kronecker, y toma la unidad de valor cuando sus dos índices son iguales, y cero en caso contrario. Se deduce de Ecuaciones\(\ref{4.3.8}\) y\(\ref{4.3.11}\) que
\[ c_i = \int_{-\infty}^\infty \phi_i^\ast \psi dx. \label{4.3.12} \]
Así, los coeficientes de expansión en Ecuación se\(\ref{4.3.12}\) determinan fácilmente, dada la función de onda\(\psi\) y los autoestados\(\phi_i\). Además, si\(\psi\) es una función de onda normalizada correctamente, entonces Ecuaciones\(\ref{4.3.8}\) y\(\ref{4.3.11}\) rendimiento
\[ \sum_i \vert c_i\vert^2 =1. \label{4.3.13} \]
Se dice que el colapso de la función de onda ocurre cuando una función de onda, inicialmente en una superposición de varios autoestados, parece reducirse a un solo estado propio (por “observación”). Una partícula (o un sistema en general) se puede encontrar en un estado dado\(\psi(x,t)\). Supongamos que ahora se realiza una medición en la función de onda para caracterizar una propiedad específica del sistema.
Matemáticamente, un operador\(\hat{A}\) está asociado a este proceso de medición, el cual se supone que tiene un conjunto ortonormal completo de valores propios:\(\{ \phi_i \}\) que suele ser un conjunto infinito de funcionales que dependen del número cuántico\(n\). La función de onda se\(\Psi\) puede expandir y se puede seleccionar un conjunto de funciones base para especificar que la función de onda es los coeficientes\(\{c_n\}\) de la expansión. Por lo tanto, si el sistema está perturbado, entonces su función de onda tendrá otro conjunto de coeficientes\(\{c'_n\}\).
Si la función de onda está en el estado propio del operador, entonces cada medición a través de ese operador dará el mismo resultado.
Colaboradores y Atribuciones
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
- Wikiversity

