4.5: Las funciones propias de los operadores son ortogonales
- Page ID
- 79320
- Comprender las propiedades de un operador hermitiano y sus propios estados asociados
- Reconocer que todos los obervables experimentales son obtenidos por operadores hermitianos
La consideración de la descripción mecánica cuántica de la partícula en una caja expuso dos propiedades importantes de los sistemas mecánicos cuánticos. Vimos que las funciones propias del operador hamiltoniano son ortogonales, y también vimos que la posición y el impulso de la partícula no se podían determinar exactamente. Ahora examinamos la generalidad de estas percepciones declarando y probando algunos teoremas fundamentales. Estos teoremas utilizan la propiedad hermitiana de operadores mecánicos cuánticos que corresponden a observables, lo que se discute primero.
Operadores hermitianos
Dado que los valores propios de un operador mecánico cuántico corresponden a cantidades medibles, los valores propios deben ser reales y, en consecuencia, un operador mecánico cuántico debe ser hermitiano. Para demostrarlo, partimos de las premisas que\(ψ\) y\(φ\) son funciones,\(\int d\tau\) representa la integración sobre todas las coordenadas, y el operador\(\hat {A}\) es hermitiano por definición si
\[ \int \psi ^* \hat {A} \psi \,d\tau = \int (\hat {A} ^* \psi ^* ) \psi \,d\tau \label {4-37} \]
Esta ecuación significa que el complejo conjugado de\(\hat {A}\) puede operar\(ψ^*\) para producir el mismo resultado después de la integración que\(\hat {A}\) operar sobre\(φ\), seguido de la integración. Para probar que un operador mecánico cuántico\(\hat {A}\) es hermitiano, considere la ecuación de valor propio y su complejo conjugado.
\[\hat {A} \psi = a \psi \label {4-38} \]
\[\hat {A}^* \psi ^* = a^* \psi ^* = a \psi ^* \label {4-39} \]
Tenga en cuenta que\(a^* = a\) debido a que el valor propio es real. Multiplicar Ecuación\(\ref{4-38}\) y\(\ref{4-39}\) desde la izquierda por\(ψ^*\) y\(ψ\), respectivamente, e integrar en todo el rango de todas las coordenadas. Tenga en cuenta que\(ψ\) se normaliza. Los resultados son
\[ \int \psi ^* \hat {A} \psi \,d\tau = a \int \psi ^* \psi \,d\tau = a \label {4-40} \]
\[ \int \psi \hat {A}^* \psi ^* \,d \tau = a \int \psi \psi ^* \,d\tau = a \label {4-41} \]
Dado que ambas integrales son iguales\(a\), deben ser equivalentes.
\[ \int \psi ^* \hat {A} \psi \,d\tau = \int \psi \hat {A}^* \psi ^* \,d\tau \label {4-42} \]
El operador que actúa sobre la función,
\[\hat {A}^* \int \psi ^* \hat {A} \psi \,d\tau = \int \psi \hat {A} ^* \psi ^* \,d\tau_* \nonumber \]
produce una nueva función. Dado que las funciones conmutan, la ecuación se\(\ref{4-42}\) puede reescribir como
\[ \int \psi ^* \hat {A} \psi d\tau = \int (\hat {A}^*\psi ^*) \psi d\tau \label{4-43} \]
Esta igualdad significa que\(\hat {A}\) es hermitiano.
Las funciones propias de un operador hermitiano son ortogonales si tienen diferentes valores propios.
Debido a este teorema, podemos identificar funciones ortogonales fácilmente sin tener que integrar o realizar un análisis basado en la simetría u otras consideraciones.
\(ψ\)y\(φ\) son dos funciones propias del operador  con valores propios reales\(a_1\) y\(a_2\), respectivamente. Dado que los valores propios son reales,\(a_1^* = a_1\) y\(a_2^* = a_2\).
\[\hat {A} \psi = a_1 \psi \nonumber \]
\[\hat {A}^* \psi ^* = a_2 \psi ^* \nonumber \]
Multiplique la primera ecuación por\(φ^*\) y la segunda por\(ψ\) e integre.
\[\int \psi ^* \hat {A} \psi \,d\tau = a_1 \int \psi ^* \psi \,d\tau \nonumber \]
\[\int \psi \hat {A}^* \psi ^* \,d\tau = a_2 \int \psi \psi ^* \,d\tau \label {4-45} \]
Restar las dos ecuaciones en la Ecuación\ ref {4-45} para obtener
\[\int \psi ^*\hat {A} \psi \,d\tau - \int \psi \hat {A} ^* \psi ^* \,d\tau = (a_1 - a_2) \int \psi ^* \psi \,d\tau \label {4-46} \]
El lado izquierdo de la Ecuación\ ref {4-46} es cero porque\(\hat {A}\) es un rendimiento hermitiano
\[ 0 = (a_1 - a_2 ) \int \psi ^* \psi \, d\tau \label {4-47} \]
Si\(a_1\) y\(a_2\) en la Ecuación\ ref {4-47} no son iguales, entonces la integral debe ser cero. Este resultado demuestra que las funciones propias no degeneradas del mismo operador son ortogonales.
\(\square\)
Dos funciones de onda,\(\psi_1(x)\) y\(\psi_2(x)\), se dice que son ortogonales si
\[\int_{-\infty}^{\infty}\psi_1^\ast \psi_2 \,dx = 0. \label{4.5.1} \]
Considere dos autoestados de\(\hat{A}\),\(\psi_a(x)\) y\(\psi_{a'}(x)\), que corresponden a los dos autovalores diferentes\(a\) y\(a'\), respectivamente. Por lo tanto,
\[A\psi_a = a \psi_a \label{4.5.2} \]
\[A\psi_a' = a' \psi_a' \label{4.5.3} \]
Multiplicando el complejo conjugado de la primera ecuación por\(\psi_{a'}(x)\), y la segunda ecuación por\(\psi^*_{a'}(x)\), y luego integrando sobre todo\(x\), obtenemos
\[ \int_{-\infty}^\infty (A \psi_a)^\ast \psi_{a'} dx = a \int_{-\infty}^\infty\psi_a^\ast \psi_{a'} dx, \label{ 4.5.4} \]
\[ \int_{-\infty}^\infty \psi_a^\ast (A \psi_{a'}) dx = a' \int_{-\infty}^{\infty}\psi_a^\ast \psi_{a'} dx. \label{4.5.5} \]
Sin embargo, a partir de la Ecuación\(\ref{4-46}\), los lados izquierdos de las dos ecuaciones anteriores son iguales. De ahí que podamos escribir
\[(a-a') \int_{-\infty}^\infty\psi_a^\ast \psi_{a'} dx = 0. \nonumber \]
Por suposición,\(a \neq a'\), cediendo
\[\int_{-\infty}^\infty\psi_a^\ast \psi_{a'} dx = 0. \nonumber \]
En otras palabras, los estados propios de un operador hermitiano correspondientes a diferentes valores propios son automáticamente ortogonales.
Los valores propios de los operadores asociados a mediciones experimentales son todos reales.
Dibuja gráficas y utilízalas para mostrar que las funciones de onda de partículas en una caja son ortogonales entre sí\(\psi(n = 2)\) y\(\psi(n = 3)\) son ortogonales entre sí.
Solución
Las dos funciones de onda PIB son cualitativamente similares cuando se trazan
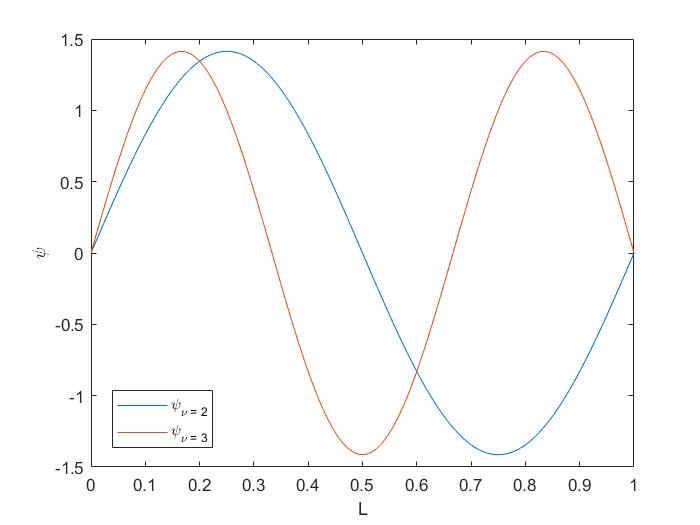
Estas funciones de onda son ortogonales cuando
\[\int_{-\infty}^{\infty} \psi(n=2) \psi(n=3) dx =0 \nonumber \]
y cuando se sustituyen las funciones de onda PIB esta integral se convierte en
\[\begin{align*} \int_0^L \sqrt{\dfrac{2}{L}} \sin \left( \dfrac{2n}{L}x \right) \sqrt{\dfrac{2}{L}} \sin \left( \dfrac{2n}{L}x \right) dx &= ? \\[4pt] \dfrac{2}{L} \int_0^L \sin \left( \dfrac{2}{L}x \right) \sin \left( \dfrac{3}{L}x \right) &= ? \end{align*} \nonumber \]
Podemos expandir el integrando usando identidades trigonométricas para ayudar a resolver la integral, pero es más fácil aprovechar la simetría del integrando, específicamente, la función de\(\psi(n=2)\) onda es par (curvas azules en la figura anterior) y la\(\psi(n=3)\) es impar (curva púrpura). Su producto (pares veces impares) es una función impar y la integral sobre una función impar es cero. Por lo tanto\(\psi(n=2)\) y las\(\psi(n=3)\) funciones de onda son ortogonales.
Esto se puede repetir un número infinito de veces para confirmar que todo el conjunto de ondas PIB son mutuamente ortogonales como lo garantiza el Teorema de Ortogonalidad.
Ortogonalidad de los EIGENESTADOS DEGENERADOS
Considerar dos autoestados de\(\hat{A}\),\(\psi_a\) y\(\psi'_a\), que corresponden al mismo valor propio,\(a\). Dichos autoestados se llaman degenerados. La prueba anterior de la ortogonalidad de diferentes estados propios falla para los autoestados degenerados. Tenga en cuenta, sin embargo, que cualquier combinación lineal de\(\psi_a\) y también\(\psi'_a\) es un estado propio de\(\hat{A}\) correspondiente al valor propio\(a\). Así, aunque\(\psi_a\) y no\(\psi'_a\) sean ortogonales, siempre podemos elegir dos combinaciones lineales de estos autoestados que son ortogonales. Por ejemplo, si\(\psi_a\) y\(\psi'_a\) están normalizados correctamente, podemos definir la integral de superposición
\[S= \int_{-\infty}^\infty \psi_a^\ast \psi_a' dx ,\label{ 4.5.10} \]
Se demuestra fácilmente (pero no aquí) que
\[\psi_a'' = \frac{\vert S\vert}{\sqrt{1-\vert S\vert^2}}\left(\psi_a - S^{-1} \psi_a'\right) \label{4.5.11} \]
es un estado propio correctamente normalizado de\(\hat{A}\), correspondiente al valor propio\(a\), que es ortogonal a\(\psi_a\). Es sencillo generalizar el argumento anterior a tres o más autoestados degenerados. De ahí que concluimos que los estados propios de un operador hermitiano son, o pueden elegirse para ser, mutuamente ortogonales.
Las funciones propias degeneradas no son automáticamente ortogonales, sino que se pueden hacer matemáticamente a través de la ortogonalización Gram-Schmidt.
El teorema anterior sostiene que si los valores propios de dos funciones propias son iguales entonces se dice que las funciones son degeneradas y se pueden formar combinaciones lineales de las funciones degeneradas que serán ortogonales entre sí. Dado que las dos funciones propias tienen los mismos valores propios, la combinación lineal también será una función propia con el mismo valor propio. La prueba de este teorema nos muestra una manera de producir funciones degeneradas ortogonales.
Si\(\psi_a\) y\(\psi'_a\) son degenerados, pero no ortogonales, podemos definir una nueva función de onda compuesta\(\psi_a'' = \psi'_a - S\psi_a\) donde\(S\) está la integral de superposición:
\[S= \langle \psi_a | \psi'_a \rangle \nonumber \]
entonces\(\psi_a\) y\(\psi_a'' \) será ortogonal.
\[\begin{align*} \langle \psi_a | \psi_a'' \rangle &= \langle \psi_a | \psi'_a - S\psi_a \rangle \\[4pt] &= \cancelto{S}{\langle \psi_a | \psi'_a \rangle} - S \cancelto{1}{\langle \psi_a |\psi_a \rangle} \\[4pt] &= S - S =0 \end{align*} \nonumber \]
\(\square\)
Encontrar\(N\) que normaliza\(\psi\) si\(\psi = N(φ_1 − Sφ_2)\) donde\(φ_1\) y\(φ_2\) se normalizan las funciones de onda y\(S\) es su solapamiento integral.
\[S= \langle φ_1 | φ_2 \rangle \nonumber \]
- Contestar
-
Recuerda que para normalizar una función de onda arbitraria, encontramos una constante\(N\) tal que\(\langle \psi | \psi \rangle = 1\). Esto equivale al siguiente procedimiento:
\[ \begin{align*} \langle\psi | \psi\rangle =\left\langle N\left(φ_{1} - Sφ_{2}\right) | N\left(φ_{1} - Sφ_{2}\right)\right\rangle &= 1 \\[4pt] N^2\left\langle \left(φ_{1} - Sφ_{2}\right) | \left(φ_{1}-Sφ_{2}\right)\right\rangle &=1 \\[4pt] N^2 \left[ \cancelto{1}{\langle φ_{1}|φ_{1}\rangle} - S \cancelto{S}{\langle φ_{2}|φ_{1}\rangle} - S \cancelto{S}{\langle φ_{1}|φ_{2}\rangle} + S^2 \cancelto{1}{\langle φ_{2}| φ_{2}\rangle} \right] &= 1 \\[4pt] N^2(1 - S^2 \cancel{-S^2} + \cancel{S^2})&=1 \\[4pt] N^2(1-S^2) &= 1 \end{align*} \nonumber \]
por lo tanto
\[N = \dfrac{1}{\sqrt{1-S^2}} \nonumber \]
Concluimos que los estados propios de los operadores son, o pueden elegirse para ser, mutuamente ortogonales.
Colaboradores y Atribuciones
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)


\[ \int \psi'_a^* \psi_a d\tau \nonumber \]
entonces\(\psi_a\) y\(Φ\) será ortogonal.
\[ \begin{align*} \int \psi_A^* Φ d\tau &= \int \psi_a^* (\psi'_a - S \psi_a ) d\tau \\[4pt] &= \int \psi_a^* \psi'_a d\tau - S \int \psi_a^*\psi_a d\tau \\[4pt] &= S - S = 0 \end{align*} \nonumber \]