2.9: Energía de estabilización de campo de ligando

Última actualización
Guardar como PDF

Page ID: 79539

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Existe una variación sobre cómo pensar en d diagramas de división orbitales que pueden ser útiles para decidir cómo se configuran los d electrones en complejos de metales de transición. Podemos usar los niveles de energía relativa de los orbitales d en un complejo dado para calcular si la energía general sería mayor o menor en un caso de giro alto versus un caso de giro bajo, por ejemplo. El cálculo nos proporciona un valor que se denomina energía de estabilización del campo del ligando. Aunque hemos estado pensando en la unión en complejos de metales de transición en términos de ideas orbitales moleculares, la energía de estabilización de campo de ligandos en realidad tiene sus raíces en un enfoque separado llamado teoría de campos cristalinos.

Historia de origen

La teoría del campo cristalino fue desarrollada independientemente alrededor de 1930 por el físico alemán Hans Bethe y el físico estadounidense John Hasbrouck van Vleck; los dos más tarde se convirtieron en profesores de física en Cornell y Harvard, respectivamente. De hecho, es anterior al enfoque orbital molecular que hemos estado usando hasta ahora, pero llega a conclusiones similares sobre las configuraciones de electrones de metales de transición.

Ambos científicos estaban interesados en las propiedades magnéticas de los metales y las sales metálicas. Sabían que estas propiedades estaban relacionadas con electrones desapareados. Los compuestos con electrones desapareados son atraídos por campos magnéticos, mientras que los compuestos que tienen solo electrones emparejados no lo son. Se interesaron por los factores que influyeron en la configuración de electrones d de las sales de metales de transición, ya que cómo se llenaron los electrones d podría resultar en diferentes números de electrones desapareados. Esas diferencias influyeron en la fuerza en que los compuestos interactuaban con los campos magnéticos.

La teoría del campo cristalino no considera ninguna interacción de unión en compuestos de metales de transición. Se centra únicamente en la repulsión entre los electrones en un anión y los electrones en un catión metálico. Por supuesto, todos estos electrones tienen cargas negativas. A medida que un anión se acerca a un metal, razonaron los físicos, ambos conjuntos de electrones experimentarían fuerzas repulsivas que aumentarían su nivel de energía.

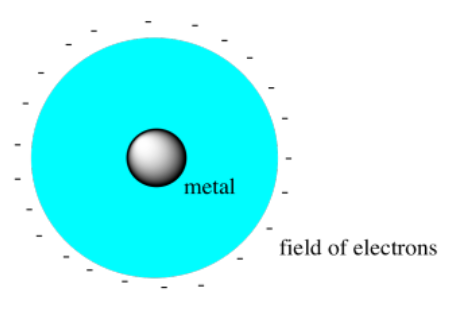
Si el metal estuviera rodeado por un campo esférico de electrones (a los físicos les gusta suponer que las cosas son esféricas porque facilita las matemáticas), entonces todos los electrones del metal serían elevados igualmente altos en energía por estas fuerzas repulsivas.

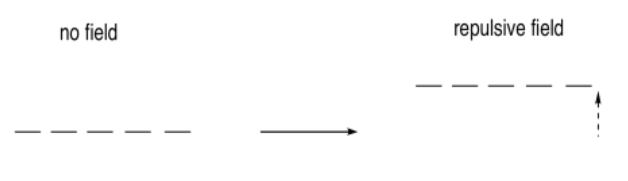
Pero en una sal metálica, los electrones no se acercan al metal desde todas las direcciones. La geometría entra por el hecho de que los cationes y aniones se agrupan en matrices específicas. Por ejemplo, si un catión metálico está sentado en un agujero octaédrico, los electrones solo se acercarían desde seis direcciones: en cada extremo de los ejes x, y y z.

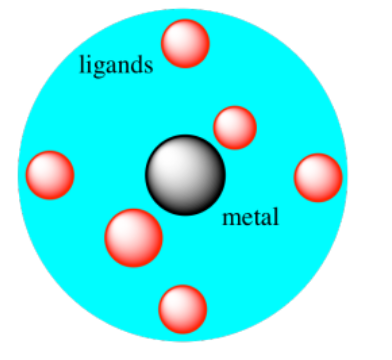
En ese caso, solo los electrones en los orbitales d que estaban alineados a lo largo de los ejes x, y y z serían elevados significativamente por repulsión con los electrones que se aproximaban en los aniones. Los electrones en los orbitales fuera del eje serían más bajos en energía de lo que habrían sido en un campo perfectamente esférico.

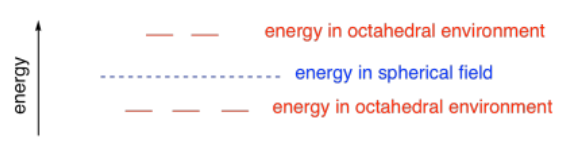
Posteriormente, los científicos adaptaron esta idea a los complejos de coordinación octaédricos, en los que el metal se asienta en medio de seis ligandos en lugar de empaquetarse entre seis aniones.

Ese resultado lleva a una imagen bastante similar a la que obtenemos de la teoría orbital molecular, al menos en lo que respecta a los orbitales d. De hecho, el verdadero enfoque matemático de la teoría orbital molecular sí toma en cuenta estas repulsiones electrón-electrónico, pero también influye en las atracciones entre los electrones de los ligandos y el núcleo del metal (y viceversa). La mayor diferencia es que la teoría orbital molecular incluye lo que sucede con la energía cinética de los pares solitarios del ligando a medida que se comparten con el metal (baja; esa es una gran parte de por qué se forman los enlaces).

Aplicación

Realmente no hay que apreciar de dónde vino este enfoque para poder ver cómo se usa comúnmente. Si tomamos los orbitales de cinco d después de haber sido colocados en un ambiente octaédrico, vemos que están en dos niveles de energía diferentes. El nivel promedio de energía no está, como podría aparecer primero, a mitad de camino entre estos niveles. Eso es porque hay tres niveles inferiores y dos niveles superiores. El promedio es de dos quintas partes del camino hacia arriba desde los tres inferiores, o tres quintos del camino hacia abajo desde los dos primeros.

Ese nivel de energía promedio de los cinco d orbitales se llama el “baricentro”; se le asigna una energía relativa de cero. La diferencia entre el nivel superior y el nivel inferior es la división de campo; para un complejo octaédrico, a esta división de campo se le da el símbolo Δ _o; aquí, Δ representa la diferencia de energía y o significa octaédrico.

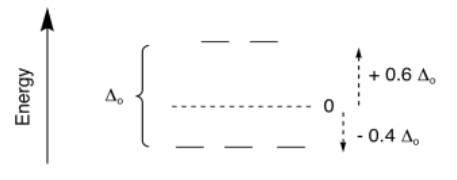
Si el baricentro está en un nivel de energía de cero, entonces los orbitales inferiores están por debajo de cero. ¿Qué tan lejos? Son dos quintas partes del total Δ _o por debajo del baricentro. Cualquier electrón en esos orbitales es -0.4Δ _o por debajo de 0 en energía. Los electrones en los orbitales superiores son +0.6Δ _o por encima de cero en energía.

Supongamos que hay cuatro electrones. Los tres primeros electrones se sientan en cada uno de los tres orbitales inferiores, los que a veces etiquetamos los orbitales t _2g.. El cuarto irá o bien al nivel superior, al que a veces llamamos el nivel e _g, o bien se emparejará con otro electrón en el nivel inferior.

Ahora podemos calcular la diferencia de energía entre estos dos posibles casos. Podemos calcular lo que se llama la energía de estabilización del campo del ligando, LFSE (a veces llamada energía de estabilización de campo cristalino, o CFSE). Es solo la suma de las energías de cada uno de los electrones.

\[LFSE = [(0.6 \times number \: of \: e_{g} \: electrons) - (0.4 \times number \: of \: t_{2g} \: electrons)] \Delta_{o}\]

o si eso es demasiada jerga,\(LFSE = [(0.6 \times \: \# upper \: e^{-}) - (0.4 \times \: \# lower \: e^{-})] \Delta_{o}\)

En el lado izquierdo, el estuche de alto giro, es decir:

\[LFSE = [(0.6 \times 1) - (0.4 \times 3)] \Delta_{o} = [0.6-1.2] \Delta_{o} = -0.6 \Delta_{o}\]

En el lado derecho, eso es

\[LFSE = [(0.6 \times 0) - (0.4 \times 4)] \Delta_{o} = -1.6 \Delta_{o}\]

Hasta ahora, ciertamente parece que el caso de bajo giro está en menor energía. Recuerde, sin embargo, que requiere que coloquemos dos electrones juntos en un mismo orbital.

Al igual que los cargos repelen. Poner estos dos electrones tan juntos va a costar algo de energía. Pero, ¿cuánto?

Esta repulsión entre un par de electrones en un orbital se llama la energía de emparejamiento (PE). Por cada par de electrones que ocupen el mismo orbital, se debe sumar esa energía para tener en cuenta esa repulsión. Como resultado, un cálculo de la energía de estabilización global incluye tanto la energía de estabilización del campo del ligando como la energía de emparejamiento.

\[SE = LFSE + PE\]

Si hubiera dos conjuntos de electrones emparejados, agregaríamos 2PE; si hubiera tres conjuntos de electrones emparejados, agregaríamos 3PE, y así sucesivamente.

En general, decidir cuantitativamente si un complejo será alto o bajo spin es la aplicación más útil de un cálculo LFSE. Sin embargo, sí hay que conocer los valores de los parámetros (la división de campo y la energía de emparejamiento) para una decisión definitiva.

Ejercicio\(\PageIndex{1}\)

Utilice los cálculos SE para determinar la estabilización tanto en casos de alto giro como en casos de centrifugado bajo. Simplemente deje su respuesta expresada en términos de Δ _o y PE.

a. Fe ⁺²

b. co ⁺²

c. Co ⁺³

d. Mn ⁺²

e. Ti ⁺³

Contestar

Contestar a

Fe ⁺²

d ⁶ giro bajo

\[SE = [-0.4(6) + 0.6(0)] \Delta _{O} + 3PE \nonumber\]

\(= [-2.4] \Delta _{O} + 3PE\)

d ⁶ alto giro

\(SE = [-0.4 (4) + 0.6(2)] \Delta _{O} + 1PE\)
\(= [-.4] \Delta _{O} + 1PE\)

Respuesta b

Co ⁺²

d ⁷ giro bajo

\[SE = [-0.4(6) + 0.6(1)] \Delta _{O} + 3PE \nonumber\]

\(= [-1.8] \Delta_{O} + 3PE\)

d ⁷ alto giro

\(SE = [-0.4(5) + 0.6(2)] \Delta _{O} + 2PE\)
\( = [-.8] \Delta _{O} + 1PE\)

Respuesta c

Co ⁺³
d ⁶ así que esto se ve igual que Fe ⁺²

Respuesta d

Mn ⁺²

d ⁵ giro bajo

\(SE = [-0.4(5) + 0.6(0)] \Delta _{O} + 2PE\)
\(=[-2.0] \Delta _{O} + 2PE\)

d ⁵ alto giro

\[SE = [-0.4(3) + 0.6(2)] \Delta _{O} + 0PE \nonumber\]

\(= [0] \Delta _{O}\)

Respuesta e

Ti ⁺³
d ¹ así que no hay posibilidad de giro bajo o alto

La Magnitud de\(\Delta_o\) and PE

Tomar en cuenta la energía de emparejamiento en este caso sugiere que se favorece el caso de alto giro. Cuesta menos energía saltar la brecha y poner un electrón en un orbital e _g alto que para emparejar electrones en un orbital t _2g de baja altitud.

Ahora mismo, pensemos en Δ _o. ¿Cuánta energía es? ¿Qué tan grande es la brecha entre los orbitales d? ¿Y cómo lo sabemos? Bueno, podemos medir fácilmente esta brecha usando un simple espectrofotómetro. Un espectrofotómetro mide cuánta luz es absorbida por una muestra. Además, mide qué colores específicos de luz son absorbidos por la muestra. A medida que sucede, la absorción de luz ultravioleta y visible por un material se asocia con electrones en ese material llegando a ser promovido a un nivel de energía superior. Brilla una luz sobre un complejo de metal de transición, y un electrón puede saltar la brecha.

Entonces todo lo que tenemos que hacer es brillar diferentes colores de luz sobre el complejo y ver si absorbe uno de los colores.

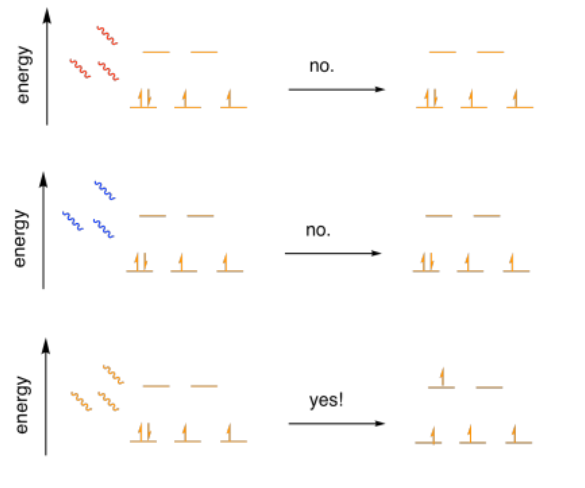
Este experimento es bastante reproducible. Un compuesto específico siempre absorberá los mismos colores de luz. Es por eso que los materiales específicos tienen colores específicos; el color que vemos representa la luz que no es absorbida por el material.

Diferentes colores de luz tienen diferentes cantidades de energía. La luz azul tiene mayor energía que la luz naranja, que tiene mayor energía que la luz roja. Max Planck y Albert Einstein resolvieron que la energía de un fotón (una “partícula” o “paquete” de luz) es directamente proporcional a la frecuencia a la que el fotón oscila o vibra. La luz azul tiene una frecuencia mayor que la luz roja, por lo que tiene mayor energía.

Planck y Einstein expresaron esta idea con una ecuación,

E = h

en el que la letra griega ν, pronunciada “noo”, representa la frecuencia (algunas personas solo usan f para frecuencia) y h representa una especie de factor de conversión llamado constante de Planck.

La luz azul tiene demasiada energía para promover un electrón al siguiente nivel de energía en este caso. Enviaría el camino del electrón más allá del siguiente nivel, y la mecánica cuántica no permite ese tipo de cosas. La luz roja no tiene suficiente energía para que el electrón llegue ahí. La luz naranja, en este caso, es la correcta. Tiene exactamente la cantidad correcta de energía para saltar la brecha.

Entonces, si conocemos la frecuencia de la luz naranja, sabemos cuánta energía hay en un fotón naranja, y sabemos cuán grande es la división de campo entre los orbitales d.

Ahora, resulta que históricamente la gente ha descrito con mayor frecuencia la luz visible en términos de longitud de onda en lugar de frecuencias. La longitud de onda es solo la distancia de un “pico” al siguiente a medida que la onda del fotón rueda a lo largo. Cuanto mayor sea la frecuencia, más cerca están estos picos juntos, y más corta es la longitud de onda. La luz azul tiene una longitud de onda más corta, alrededor de 400 nm, que la luz roja, alrededor de 700 nm. Un nanómetro (nm) es de 10 ^-9 metros (m); un metro es alrededor de una yarda.

La luz naranja tiene una longitud de onda de alrededor de 600 nm, o 600 x 10 ^-9 m, o 6 x 10 ^-7 m. Por razones en las que no entraremos, los espectroscopistas en el pasado (personas que miden la interacción de la luz y la materia) a veces prefirieron trabajar en centímetros, cm; hay 100 cm en 1 m, por lo que la luz naranja tiene una longitud de onda de 6 x 10 ^-5 cm. Ahora bien, porque sabían que había una relación inversa entre la longitud de onda y la energía (cuanto más larga es la longitud de onda, menor es la energía; cuanto más corta es la longitud de onda, mayor es la energía), simplemente tomaron el recíproco de la longitud de onda en centímetros para obtener un número en cm ^-1, al que llamaron número de onda. Utilizaron esto como una unidad de energía. Un fotón naranja tiene una energía de 1/0.00006 cm = 16,000 cm ^-1.

Entonces la brecha, la división de campo, Δ _o en este complejo es de 16,000 cm ^-1.

Volvamos a nuestra comparación entre el estuche de alto y bajo giro. Para un giro alto, eso es:

\[LFSE = [(0.6 \times 1) - (0.4 \times 3)] \Delta_{o} = [0.6 -1.2] \Delta_{o} = -0.6 \Delta_{o} = -0.6 \times 16000 cm^{-1} = -9600 cm^{-1}\]

Para el caso de giro bajo, eso es

\[LFSE = [(0.6 \times 0) -(0.4 \times 4)] \Delta_{o} = -1.6 \Delta_{o} = -1.6 \times 16000 cm^{-1} = -25600 cm^{-1}\]

Eso significa que el caso de bajo giro es menor en energía, por 14,000 cm ^-1. Sin embargo, todavía necesitamos incluir la energía de emparejamiento. Al igual que la división del campo, la energía de emparejamiento varía de un complejo a otro. 20,000 cm ^-1 es una estimación de estadio de una energía de emparejamiento típica.

Si usamos este valor promedio para PE en el ejemplo que estábamos discutiendo anteriormente, para el caso de alto giro:

\[SE = LFSE + PE = -9600 + 0 cm^{-1} = -9600 cm^{-1}\]

Para el caso de bajo giro,

\[SE = LFSE + PE = -25600 + 20000 cm^{-1} = -5600 cm^{-1}\]

Echemos un vistazo a algunos ejemplos reales de valores de división de campo para tener una idea de cuán grandes son y de qué factores dependen. Por ejemplo, podemos observar la carga en el ion metálico.

Tabla de Valores de División de Campo, Δ _o, en Complejos Hexaquo de Cargas Diferentes ^a
Complejo Metálico	[Mn (OH ₂) ₆] ²⁺	[Mn (OH ₂) ₆] ³⁺	[Fe (OH ₂) ₆] ²⁺	[Fe (OH ₂) ₆] ³⁺	[Co (OH ₂) ₆] ²⁺	[Co (OH ₂) ₆] ³⁺
Δ _o (cm ^-1)	7,800	21,100	10,400	13,800	9.300	18,300
a) Holleman, A. F.; Wiberg, E.; Wiberg, N. Inorganic Chemistry, 34 Ed. Prensa Académica: Berlín, 2001.

En este caso, parece que una mayor carga sobre el ion metálico da como resultado una mayor división del campo. Lo mismo sucede en los tres ejemplos: manganeso, hierro y cobalto. A medida que el ion metálico se vuelve más cargado, aumenta la atracción de los electrones d hacia el núcleo. El nivel inferior de t _2g se siente más fuertemente atraído por el núcleo porque está un poco más cerca; en consecuencia, cae un poco más que el nivel de e _g, y la brecha se hace más grande.

La carga sobre el ion metálico es uno de los dos factores clave que influyen en el tamaño de la división del campo. El otro factor es el periodo o fila en la tabla periódica.

Tabla de Valores de División de Campo, Δ _o, en Complejos de Hexammina del Grupo 9 ^{a, b}
Complejo Metálico	[Co (NH ₃) ₆] ³⁺	[Rh (NH ₃) ₆] ³⁺	[Ir (NH ₃) ₆] ³⁺
Δ _o (cm ^-1)	21,500	33,100	41,100
a) Holleman, A. F.; Wiberg, E.; Wiberg, N. Inorganic Chemistry, 34 Ed. Prensa Académica: Berlín, 2001. b) Miessler, G. L.; Tarr, D. A. Química Inorgánica, 4ta Ed. Pearson, 2010.

Al pasar de una fila a la siguiente en el grupo 9 de la tabla periódica, vemos que la división de campo aumenta en aproximadamente 10,000 cm ^-1 cada fila.

En general:

Δ _o aumenta con la carga sobre el metal
Δ _o aumenta con el periodo en la tabla periódica

El ion metálico no es el único factor que afecta la división del campo. Los ligandos también juegan un papel importante, como se ve en la siguiente tabla.

Tabla de Valores de División de Campo, Δ _o, en Complejos Surtidos ^a
Complejo Metálico	[CrCl ₆] ^3-	[CrF ₆] ^3-	[Fe (OH ₂) ₆] ²⁺	[Fe (CN) ₆] ^4-	[Co (OH ₂) ₆] ³⁺	[Co (NH ₃) ₆] ³⁺	[Co (CN) ₆] ^3-
Δ _o (cm ^-1)	13,300	15,300	10,400	33,200	18,300	23,000	33,700
a) Holleman, A. F.; Wiberg, E.; Wiberg, N. Inorganic Chemistry, 34 Ed. Prensa Académica: Berlín, 2001.

Si ordenamos estos ligandos en tres amplias categorías, podemos formar una tendencia para estos efectos. Puede ser más fácil comenzar con las tres entradas de la derecha, involucrando cobalto. El donante de oxígeno en el agua tiene dos pares solitarios, mientras que el donante de nitrógeno en amoníaco tiene solo uno. El par solitario extra permite que el agua actúe como donante π; el par solitario puede donar a un orbital en el metal para formar un enlace pi. En este caso, parece que el donador π (agua) da como resultado un Δ _o menor que el donante σ normal (amoníaco).

El ligando de cianuro tiene un átomo donador que también está participando en un enlace π dentro del ligando; existe un triple enlace entre el C y el N del cianuro. Eso significa que también hay un orbital antiadhesión asociado, π*. Ese orbital antiaglutinante plantea la posibilidad de volver a unir desde el metal. El metal puede donar al orbital π* para hacer un enlace pi. El cianuro es un aceptor π. Su división de campo es mucho mayor que la del donante sigma.

Esas conclusiones pueden confirmarse observando las entradas para hierro en el centro de la tabla. El cianuro es un aceptor π mientras que el agua es un donador π. La división de campo en el complejo aquo debe ser mucho menor que la división de campo en el complejo ciano, y lo es.

Las dos entradas para el cromo de la izquierda muestran haluros, los cuales son donadores π. Ilustran un factor que puede usarse para predecir la intensidad de campo entre dos ligandos del mismo grupo, como dos donadores p o dos aceptores π. En general, cuanto más básico es el ligando, mayor es la división del campo. El ion fluoruro es más básico que el ion cloruro (porque el cloruro es un anión más estable que el fluoruro) por lo que resulta en un valor ligeramente mayor de Δ _o.

Para estimar a fondo la energía de estabilización, también necesitamos valores confiables para la energía de emparejamiento. Las energías de emparejamiento se pueden calcular para iones metálicos libres; se pueden aplicar factores de corrección para llegar a un valor correspondiente en un complejo. En general, los valores en los complejos de coordinación son algo menores que los valores en iones metálicos libres. En la siguiente tabla, hemos hecho una estimación general de que el valor en el complejo es aproximadamente 20% menor que en el ión metálico libre.

Tabla de Energías de Emparejamiento, PE, en Iones Libres, con PE Estimado en Complejos
Ion Metálico	Mn ²⁺	Mn ³⁺	Fe ²⁺	Fe ³⁺	Co ³⁺	Ru ³⁺
PE, ion libre (cm ^-1)	28,000	25,500	17,700	30,100	21,100	~15.000 ^b
PE, complejo (est., cm ^-1)	20,400	22,900	14,200	24,100	16,900	~12,000 ^b
a) Holleman, A. F.; Wiberg, E.; Wiberg, N. Inorganic Chemistry, 34 Ed. Prensa Académica: Berlín, 2001. b) Estimación.

Si comparamos las energías de emparejamiento de los iones 2+ con las de los iones 3+, vemos que siempre es menor en el ion más altamente cargado. Eso es lo opuesto a la tendencia en Δ _o. La energía de emparejamiento depende en gran medida del tamaño del ion. Cuanto más pequeño es el ion, más pequeño es el orbital y más repulsión entre dos electrones en el mismo orbital. Debido a que un ion Mn ³⁺ es más pequeño que un ion Mn ²⁺ (la Ley de Coulomb dice que hay mayor atracción para los electrones en el primer caso, por lo que el ion se contrae), un par de electrones en Mn ³⁺ está más cerca que un par de electrones en Mn ²⁺.

En general, las energías de emparejamiento también se hacen más pequeñas al bajar una columna en la tabla periódica. Los metales de transición de la segunda fila son mayores que los metales de transición de la primera fila, por lo que la energía de emparejamiento es menor en la segunda fila que en la primera Los metales de transición de la tercera fila tienen aproximadamente el mismo tamaño que los metales de la primera fila, por lo que las energías de emparejamiento son similares a las de la segunda fila. Eso se debe a un fenómeno llamado “la contracción de lantánidos”: los metales de transición de la tercera fila contienen un conjunto extra de protones en sus núcleos debido a los elementos del bloque f que tienen ante ellos; en consecuencia, son un poco más pequeños de lo que cabría esperar.

Ejercicio\(\PageIndex{2}\)

Compare las energías de emparejamiento con los valores de división de campo para determinar si los siguientes complejos serían de alto giro o de giro bajo.

a) Mn (OH ₂) ₆ ²⁺ b) Fe (CN) ₆ ^4- c) Co (NH ₃) ₆ ³⁺

Contestar
Contestar a: Δ _o < PE, por lo tanto de alto giro.
Respuesta b: Δ _o > PE, por lo que de alto giro.
Respuesta c: Δ _o > PE, por lo que de alto giro.

Otras geometrías

La teoría del campo cristalino también se ha aplicado a otras geometrías de compuestos de coordinación. Una vez más, en términos del diagrama de división orbital d, los resultados son similares a lo que vemos en la teoría orbital molecular. Para la geometría tetraédrica, que es la geometría más común cuando el número de coordinación es cuatro, nuevamente obtenemos un conjunto de dos orbitales altos y tres orbitales inferiores.

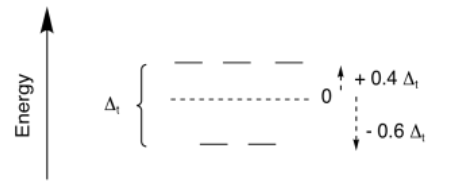
La división global se expresa como Δ _t; la t significa tetraédrica. Sin embargo, a veces es útil comparar diferentes geometrías. En la teoría del campo cristalino, se puede demostrar que la cantidad de división en un campo tetraédrico es mucho menor que en un campo octaédrico. En general, Δ _t = 4/9 Δ _o.

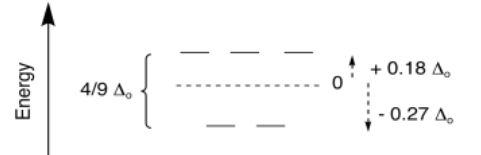
Por lo general, no usaríamos la teoría de campos cristalinos para decidir si un metal es más probable que adopte una geometría tetraédrica o octaédrica. En la mayoría de los casos, el resultado depende más fuertemente de factores distintos de las d energías orbitales. Por ejemplo, tal vez un complejo estaría demasiado abarrotado con seis ligandos, por lo que sólo se une a cuatro; se vuelve tetraédrico en lugar de octaédrico. O tal vez un metal no tiene suficientes electrones en su caparazón de valencia, por lo que une un par de ligandos más; se vuelve octaédrico en lugar de tetraédrico.

Sin embargo, esta comparación entre Δ _o y Δ _t ayuda a explicar por qué los complejos tetraédricos son mucho más propensos a adoptar configuraciones de alto espín que los complejos octaédricos. La división es menor en geometría tetraédrica, por lo que la energía de emparejamiento es más probable que se convierta en el factor decisivo allí que en los casos octaédricos.

Ejercicio\(\PageIndex{3}\)

Los complejos tetraédricos son bastante comunes para los metales d6 de alto espín, aunque la regla de 18 electrones sugiere que se deben formar complejos octaédricos. En contraste, los complejos d6 de bajo espín no suelen formar complejos tetraédricos. Utilizar cálculos de energías de estabilización para explicar por qué.

Contestar

alto giro D ⁶

octaédrico

\[SE = [2(0.6) - 4(0.4)] \Delta _{O} + PE \nonumber\]

\[SE = -0.4 \Delta _{O} + PE \nonumber\]

tetraédrico

\[SE = [3(0.4)- 3(0.6)] \frac{4}{9} \Delta_{O} + PE \nonumber\]

\[SE = -0.6 \Delta _{O} + PE \nonumber\]

\[\Delta SE = SE_{oh} - SE_{td} = -0.4 \Delta _{O} + PE - (-0.6 \Delta _{O} + PE) = + 0.2 \Delta_{O} \nonumber\]

Esta es una ligera preferencia por el tetraédrico.

bajo giro D ⁶

octaédrico

\[SE = [0(0.6) -6(0.4)] \Delta_{O} + 3PE \nonumber\]

\[SE = -2.4 \Delta _{O} + 3PE \nonumber\]

tetraédrico

\[SE = [2(0.4) - 4(0.6)] \frac{4}{9} \Delta _{O} + 2PE \nonumber\]

\[SE = -1.6 \Delta_{O} + PE \nonumber\]

\[\Delta SE = SE_{oh} - SE_{td} = -2.4 \Delta _{o} + 3PE-(-1.6 \Delta _{o} + 2PE) = -0.8 \Delta_{o} + PE \nonumber\]

Esta es una preferencia por octaédrica, aunque sería compensada por la energía de emparejamiento.

La teoría de campos cristalinos también se ha utilizado para determinar las divisiones entre los orbitales en una geometría plana cuadrada. Ese es un caso mucho más complicado, porque hay cuatro niveles diferentes. Una vez más, los niveles de energía a menudo se expresan en términos de Δ _o.

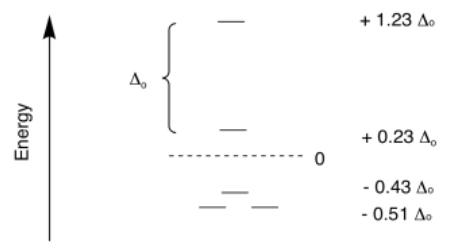
Podríamos usar un cálculo de la energía de estabilización para predecir si un complejo en particular es probable que adopte una geometría tetraédrica o una geometría plana cuadrada. Ambas geometrías son posibles, por lo que sería útil poder predecir qué geometría ocurre en qué caso. Sin embargo, al igual que en el caso de comparar geometrías octaédricas y tetraédricas, hay otro factor que muchas veces es más importante.

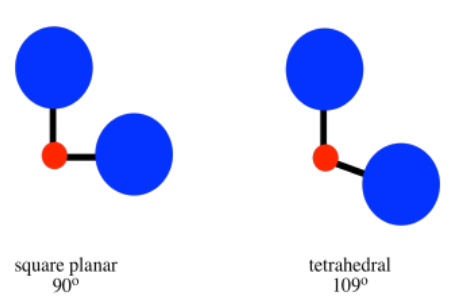
Ese factor es el hacinamiento estérico. En un tetraedro, todos los ligandos están a 109 ^o entre sí. En una geometría plana cuadrada, los ligandos están a solo 90 ^o de distancia entre sí. La geometría tetraédrica siempre está menos abarrotada que la plana cuadrada, por lo que ese factor siempre proporciona un sesgo hacia la geometría tetraédrica. Como resultado, podríamos esperar que la geometría plana cuadrada ocurra solo cuando los esteros son muy superados por la energía de estabilización del campo del ligando.

Ejercicio\(\PageIndex{4}\)

Los ejemplos más comunes de complejos planos cuadrados tienen metales que son d ⁸. Utilice los cálculos de la energía de estabilización para explicar por qué si el complejo es:

(a) giro bajo

(b) alto giro

Contestar

Contestar a

alto giro D ⁸

plano cuadrado

\[SE = [1.23 + 0.23 - 2(0.43) - 4(0.51)] \Delta_{O} + 3PE \nonumber\]

\[SE = -1.44 \Delta _{O} + 3PE \nonumber\]

tetraédrico

\[SE = [4(0.4) -4(0.6)] \frac{4}{9} \Delta + 3PE \nonumber\]

\[SE = -0.36 \Delta_{O} + 3PE \nonumber\]

\[\Delta = \Delta SE = SE_{sq} - SE_{td} = -1.44 \Delta _{O} + 3PE -(-0.36 \Delta_{O} + 3PE) = -1.08 \Delta_{O} \nonumber\]

Esta es una preferencia apreciable por el plano cuadrado.

Respuesta b

bajo giro D ⁸

plano cuadrado

\[SE = [0 + 2(0.23) - 2(0.43) - 4(0.51)] \Delta_{O} + 4PE \nonumber\]

\[SE = -2.44 \Delta_{O} + 4PE \nonumber\]

tetraédrico = igual que antes (ls = hs para d ⁸ tetraédrico)

\[\Delta SE = SE_{sq} - SE_{td} = -2.44 \Delta_{O} + 3PE -(-0.36 \Delta_{O} + 3PE) = -2.08 \Delta_{O} + PE \nonumber\]

Esta es una preferencia aún más apreciable por el plano cuadrado, aunque se ve compensado por la energía de emparejamiento. La energía de emparejamiento tendría que ser el doble de grande que Δ _o para compensar completamente el LFSE.