3.2: El significado de la medida
- Page ID
- 70982
Asegúrese de comprender a fondo las siguientes ideas esenciales que se han presentado anteriormente. Es especialmente importante que conozcas los significados precisos de todos los términos resaltados en el contexto de este tema.
- Dé un ejemplo de un valor numérico medido, y explique qué lo distingue de un número “puro”.
- Dar ejemplos de errores aleatorios y sistemáticos en las mediciones.
- Encuentra el valor medio de una serie de medidas similares.
- Indicar los principales factores que afectan la diferencia entre el valor medio de una serie de mediciones, y el “valor verdadero” de la cantidad que se está midiendo.
- Calcular las precisiones absolutas y relativas de una medida dada, y explicar por qué esta última es generalmente más útil.
- Distinguir entre la exactitud y la precisión de un valor medido, y en los roles de error aleatorio y sistemático.
La distancia exacta entre el labio superior y la punta de la aleta dorsal se ocultará para siempre en una niebla de incertidumbre. El ángulo en el que sujetamos las pinzas y la fuerza con la que las cerramos sobre el objeto nunca serán exactamente reproducibles. Una limitación más fundamental ocurre cuando tratamos de comparar una cantidad continuamente variable como la distancia con los intervalos fijos en una escala de medición; ¡entre 59 y 60 mils hay la misma infinidad de distancias que existe entre 59 y 60 millas!
Imagen de Stephen Winsor; utilizada con permiso del artista.
El “verdadero valor” de una cantidad medida, si existe, siempre nos eludirá; lo mejor que podemos hacer es aprender a hacer un uso significativo (¡y evitar un mal uso!) de los números que leemos de nuestros dispositivos de medición.
¡La incertidumbre es cierta!
En la ciencia, hay números y hay “números”. Lo que normalmente pensamos como un “número” y nos referiremos aquí como un número puro es precisamente eso: una expresión de un valor preciso. El primero de estos que alguna vez aprendiste fueron los números de conteo, o enteros; más tarde, te introdujeron los números decimales, y los números racionales, que incluyen números como 1/3 y π (pi) que no pueden expresarse como valores decimales exactos.
El otro tipo de cantidad numérica que encontramos en las ciencias naturales es un valor medido de algo: la longitud o el peso de un objeto, el volumen de un fluido, o tal vez la lectura en un instrumento. Si bien expresamos estos valores numéricamente, sería un error considerarlos como el tipo de números puros descritos anteriormente.
¿Confundir? Supongamos que nuestro instrumento tiene un indicador como el que ve aquí. El puntero se mueve hacia arriba y hacia abajo para mostrar el valor medido en esta escala. ¿Qué número escribirías en tu cuaderno al grabar esta medición? Claramente, el valor está en algún lugar entre 130 y 140 en la escala, pero las graduaciones nos permiten ser más exactos y situar el valor entre 134 y 135. El indicador apunta más de cerca a este último valor, y podemos dar un paso más estimando el valor tal vez como 134.8, por lo que este es el valor que reportarías para esta medición.
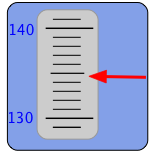
Ahora bien, aquí está lo importante a entender: aunque “134.8” es en sí mismo un número, la cantidad que estamos midiendo casi con certeza no es 134.8— al menos, no exactamente. El motivo es obvio si observa que la escala del instrumento es tal que apenas somos capaces de distinguir entre 134.7, 134.8 y 134.9. Al reportar el valor 134.8 efectivamente estamos diciendo que el valor probablemente esté en algún lugar con el rango de 134.75 a 134.85. Es decir, hay una incertidumbre de ±0.05 unidad en nuestra medida.
Todas las mediciones de cantidades que pueden asumir un rango continuo de valores (longitudes, masas, volúmenes, etc.) constan de dos partes: el valor reportado en sí (nunca un número exactamente conocido), y la incertidumbre asociada a la medición. Por “error”, no nos referimos solo a errores descarados, como el uso incorrecto de un instrumento o la falta de lectura adecuada de una escala; aunque a veces ocurren errores tan groseros, suelen arrojar resultados lo suficientemente inesperados como para llamar la atención sobre sí mismos.
Todas las mediciones están sujetas a error lo que contribuye a la incertidumbre del resultado. Por “error”, no nos referimos solo a errores descarados, como el uso incorrecto de un instrumento o la falta de lectura adecuada de una escala; aunque a veces ocurren errores tan groseros, suelen arrojar resultados lo suficientemente inesperados como para llamar la atención sobre sí mismos.
Cuando se mide un volumen o peso, se observa una lectura en una báscula de algún tipo. Las escalas, por su propia naturaleza, se limitan a incrementos fijos de valor, indicados por las marcas de división. Las cantidades reales que estamos midiendo, en contraste, pueden variar continuamente, por lo que existe una limitación inherente en cuán finamente podemos discriminar entre dos valores que caen entre las divisiones marcadas de la escala de medición. El mismo problema persiste si sustituimos un instrumento por una pantalla digital; siempre habrá algún punto en el que algún valor que se encuentre entre las dos divisiones más pequeñas debe alternar arbitrariamente entre dos números en la pantalla de lectura. Esto introduce un elemento de aleatoriedad en el valor que observamos, aunque el valor “verdadero” permanezca sin cambios.
Cuanto más sensible sea el instrumento de medición, menos probable es que dos mediciones sucesivas de una misma muestra den resultados idénticos. En el ejemplo que discutimos anteriormente, distinguir entre los valores 134.8 y 134.9 puede ser demasiado difícil de hacer de manera consistente, por lo que dos observadores independientes pueden registrar valores diferentes incluso al visualizar la misma lectura. Cada medición también está influenciada por una gran cantidad de eventos menores, como vibraciones del edificio, fluctuaciones eléctricas, movimientos del aire y fricción en cualquier parte móvil del instrumento. Estas diminutas influencias constituyen una especie de “ruido” que también tiene un carácter aleatorio. Seamos conscientes de ello o no, todos los valores medidos contienen un elemento de error aleatorio.
Cada medición también está influenciada por una gran cantidad de eventos menores, como vibraciones del edificio, fluctuaciones eléctricas, movimientos del aire y fricción en cualquier parte móvil del instrumento. Estas diminutas influencias constituyen una especie de “ruido” que también tiene un carácter aleatorio. Seamos conscientes de ello o no, todos los valores medidos contienen un elemento de error aleatorio.
Supongamos que usted se pesa en una báscula de baño, sin darse cuenta de que el dial dice “1.5 kg” incluso antes de haber colocado su peso sobre ella. De manera similar, podrías usar una regla vieja con un extremo desgastado para medir la longitud de una pieza de madera. En ambos ejemplos, todas las mediciones posteriores, ya sea del mismo objeto o de diferentes, estarán apagadas en una cantidad constante. A diferencia del error aleatorio, que es imposible de eliminar, estos errores sistemáticos suelen ser bastante fáciles de evitar o compensar, pero sólo por un esfuerzo consciente en la realización de la observación, generalmente mediante una adecuada puesta a cero y calibración del instrumento de medición. Sin embargo, una vez que el error sistemático ha encontrado su camino en los datos, puede ser muy difícil de detectar.
La diferencia entre precisión y precisión
Tendemos a usar estos dos términos indistintamente en nuestra conversación ordinaria, pero en el contexto de la medición científica, tienen significados muy diferentes:
- La precisión se refiere a qué tan cerca corresponde el valor medido de una cantidad a su valor “verdadero”.
- La precisión expresa el grado de reproducibilidad, o concordancia entre mediciones repetidas.
La precisión, por supuesto, es el objetivo que buscamos en las mediciones científicas. Desafortunadamente, sin embargo, no hay una manera obvia de saber cuán cerca lo hemos logrado; el valor “verdadero”, ya sea de una cantidad bien definida como la masa de un objeto en particular, o una media que pertenece a una colección de objetos, nunca se puede conocer, y así nunca podremos reconocerlo si estamos lo suficientemente afortunados como para encontrarla.
Tenga en cuenta cuidadosamente que cuando hacemos mediciones reales, no hay tablero de dardos ni objetivo que permita juzgar inmediatamente la calidad del resultado. Si hacemos solo unas pocas observaciones, es posible que no podamos distinguir entre ninguno de estos escenarios. Por lo tanto, no podemos distinguir entre los cuatro escenarios ilustrados anteriormente simplemente examinando los resultados de las dos mediciones. Sin embargo, podemos juzgar la precisión de los resultados, y luego aplicar estadísticas simples para estimar qué tan cerca es probable que el valor medio refleje el valor verdadero en ausencia de error sistemático.
Más de una respuesta en Mediciones replicadas
Si deseas medir tu altura al centímetro o pulgada más cercano, o el volumen de un ingrediente líquido para cocinar a la “taza” más cercana, probablemente puedas hacerlo sin tener que preocuparte por un error aleatorio. El error seguirá estando presente, pero su magnitud será una fracción tan pequeña del valor que no se detectará. Por lo tanto, el error aleatorio no es algo que nos preocupe demasiado en nuestra vida cotidiana.
Si estamos haciendo observaciones científicas, sin embargo, hay que ser más cuidadosos, sobre todo si estamos tratando de explotar toda la sensibilidad de nuestros instrumentos de medición para lograr un resultado lo más confiable posible. Si estamos midiendo una cantidad directamente observable como el peso o volumen de un objeto, entonces una sola medición, cuidadosamente hecha y reportada con una precisión que sea consistente con la del instrumento de medición, generalmente será suficiente.
Más comúnmente, sin embargo, se nos llama a encontrar el valor de alguna cantidad cuya determinación depende de varios otros valores medidos, cada uno de los cuales está sujeto a sus propias fuentes de error. Considera un experimento común de laboratorio en el que debes determinar el porcentaje de ácido en una muestra de vinagre observando el volumen de solución de hidróxido de sodio requerido para neutralizar un volumen dado del vinagre. Se lleva a cabo el experimento y se obtiene un valor. Solo para estar en el lado seguro, repites el procedimiento en otra muestra idéntica de la misma botella de vinagre. Si realmente lo has hecho en el laboratorio, sabrás que es muy poco probable que el segundo ensayo produzca el mismo resultado que el primero. De hecho, si ejecutas una serie de determinaciones replicadas (es decir, idénticas en todos los sentidos), probablemente obtengas una dispersión de resultados.
Para entender por qué, considera todas las medidas individuales que van en cada determinación; el volumen de la muestra de vinagre, su juicio sobre el punto en el que se neutraliza el vinagre, y el volumen de solución utilizada para llegar a este punto. Y con qué precisión conoce la concentración de la solución de hidróxido de sodio, que se conformó disolviendo un peso medido del sólido en agua y luego agregando más agua hasta que la solución alcance algún volumen medido. Cada una de estas muchas observaciones está sujeta a errores aleatorios; debido a que tales errores son aleatorios, ocasionalmente pueden cancelarse, pero para la mayoría de los ensayos no tendremos tanta suerte, de ahí la dispersión en los resultados.
Una dificultad similar surge cuando necesitamos determinar alguna cantidad que describa una colección de objetos. Por ejemplo, un investigador farmacéutico necesitará determinar el tiempo requerido para que el cuerpo elimine la mitad de una dosis estándar de cierto medicamento, o un fabricante de bombillas podría querer saber cuántas horas operará un determinado tipo de bombilla antes de que se queme. En estos casos se puede determinar un valor para cualquier muestra individual con bastante facilidad, pero como no hay dos muestras (pacientes o bombillas) idénticas, nos vemos obligados a repetir la misma medición en múltiples muestras, y una vez más, nos enfrentamos a una dispersión de resultados.
Como último ejemplo, supongamos que se desea determinar el diámetro de un determinado tipo de moneda. Haces una medición y registras los resultados. Si luego realiza una medición similar a lo largo de una sección transversal diferente de la moneda, probablemente obtendrá un resultado diferente. Lo mismo sucederá si haces mediciones sucesivas en otras monedas del mismo tipo.
Aquí nos encontramos ante dos tipos de problemas. Primero, está la limitación inherente del dispositivo de medición: nunca podemos medir de manera confiable más finamente que las divisiones marcadas en la regla. En segundo lugar, no podemos suponer que la moneda sea perfectamente circular; una inspección cuidadosa probablemente revelará alguna distorsión resultante de una ligera imperfección en el proceso de fabricación. En estos casos, resulta que no hay un valor único, verdadero de ninguna de las dos cantidades que estamos tratando de medir.
Media, mediana y rango de una serie de observaciones
Existen diversas formas de expresar el promedio, o tendencia central de una serie de mediciones, siendo la media (más precisamente, la media aritmética) la más comúnmente empleada. Nuestro uso ordinario del término “promedio” también se refiere a la media. Cuando obtenemos más de un resultado para una medición dada (ya sea hecha repetidamente en una sola muestra, o más comúnmente, en diferentes muestras), el procedimiento más simple es reportar la media, o valor promedio. La media se define matemáticamente como la suma de los valores, dividida por el número de mediciones:
\[x_m = \dfrac{\displaystyle \sum_i x_i}{n} \label{mean}\]
Si no estás familiarizado con esta notación, ¡no dejes que te asuste! Tómate un momento para ver cómo expresa la oración anterior; si hay\(n\) medidas, cada una dando un valor xI, entonces sumamos sobre todas\(i\) y dividimos por\(n\) para obtener el valor medio\(x_m\). Por ejemplo, si sólo hay dos mediciones,\(x_1\) y\(x_1\), entonces la media es\((x_1 + x_2)/2\).
Calcular el valor medio del conjunto de ocho mediciones ilustradas aquí.
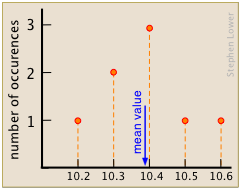
Solución
Hay ocho puntos de datos (10.4 se encontró en tres ensayos, 10.5 en dos), entonces\(n=8\). La media es (vía Ecuación\ ref {media}):
\[ \dfrac{10.2+10.3+(3 x 10.4) + 10.5+10.5+10.8}{8} = 10.4. \nonumber\]
Rango
El rango de un conjunto de datos es la diferencia entre sus valores más pequeños y mayores. Como tal, su valor refleja la precisión del resultado. Por ejemplo, los siguientes conjuntos de datos tienen el mismo promedio, pero el que tiene el rango más pequeño es claramente más preciso.
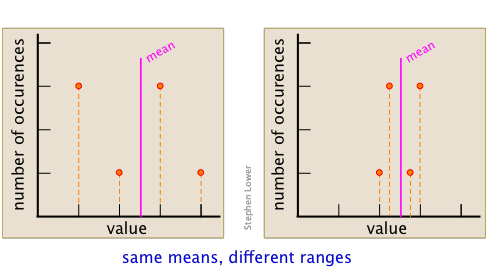
Si arregla la lista de valores medidos en orden de su magnitud, la mediana es la que tiene tantos valores por encima de ella como por debajo de ella.
Ejemplos: para el conjunto de datos [22 23 23 24 26 28] el modo sería 23.
Para un número impar de valores n, la mediana es el miembro [(n +1) /2] ésimo del conjunto. Así para [22 23 23 24 24 27], (n +1) /2 =3, entonces 23 es el valor de la mediana.
Modo
Esto se refiere al valor que se observa con mayor frecuencia en una serie de mediciones. Si dos o más valores se vinculan para la frecuencia más alta, entonces puede haber múltiples modos. El modo es más útil para describir conjuntos de datos más grandes.
Ejemplo: para el conjunto de datos [22 23 23 24 26 26] los modos son 23 y 24.
Cuantas más observaciones, más confiable es el valor medio. Si esto no es inmediatamente obvio, piénsalo de esta manera. No querría predecir el resultado de la próxima elección a partir de entrevistas con solo dos o tres votantes; querría una muestra de diez a veinte como mínimo, y si la elección es una elección nacional importante, una muestra justa requeriría de cientos a miles de personas distribuidas por todo el área geográfica y representando una variedad de grupos socioeconómicos. De igual manera, querría probar una gran cantidad de bombillas para estimar la vida media de las bombillas de ese tipo.
La teoría estadística nos dice que cuantas más muestras tengamos, mayor será la probabilidad de que la media de los resultados corresponda al valor “verdadero”, que en este caso sería la media obtenida si se pudieran tomar muestras de toda la población (de personas o de bombillas).
Este punto se puede apreciar mejor examinando los dos conjuntos de datos aquí mostrados. El conjunto de la izquierda consta de sólo tres puntos (mostrados en naranja), y da una media que está bastante alejada del valor “verdadero”, que se elige arbitrariamente para este ejemplo.
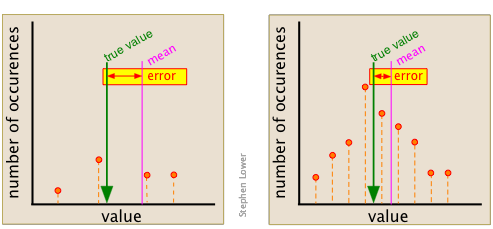
En el conjunto de datos de la derecha, compuesto por nueve mediciones, la desviación de la media del valor verdadero es mucho menor.
La desviación de la media del “valor verdadero” se hace menor cuando se hacen más mediciones.
Parcelas y puntos
Un problema similar surge cuando se intenta ajustar una curva a una serie de puntos trazados. Supongamos, por ejemplo, que la curva 1 (roja) representa la verdadera relación entre las cantidades indicadas en el eje y (variable dependiente) y las del eje x (variable independiente). Esta curva se deriva de los siete puntos indicados en la parcela.
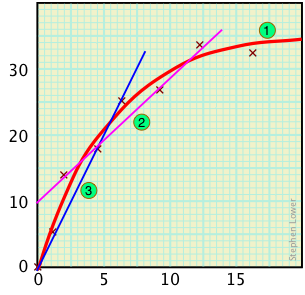
Contraste esta curva con las falsas relaciones de línea recta que podrían obtenerse si solo se hubieran registrado cuatro o tres puntos.
Incertidumbre absoluta y relativa
Si pesa 74.1 mg de una muestra sólida en una balanza de laboratorio que es precisa dentro de 0.1 miligramos, entonces es probable que el peso real de la muestra caiga en algún lugar en el rango de 74.0 a 74.2 mg; la incertidumbre absoluta en el peso que observa es 0.2 mg, o ±0.1 mg. Si usa la misma balanza para pesar 3.2914 g de otra muestra, el peso real está entre 3.2913 g y 3.2915 g, y la incertidumbre absoluta sigue siendo ±0.1 mg. Por lo tanto, la incertidumbre absoluta no está relacionada con la magnitud del valor observado.
Al expresar la incertidumbre de un valor dado en notación científica, la parte exponencial debe incluir tanto el valor en sí como la incertidumbre. Un ejemplo de la forma adecuada sería (3.19 ± 0.02) × 10 4 m.
Si bien las incertidumbres absolutas en estos dos ejemplos son idénticas, probablemente consideraríamos que la segunda medición es más precisa porque la incertidumbre es una fracción menor del valor medido. Una cantidad calculada de esta manera se conoce como la incertidumbre relativa.
Calcular las incertidumbres relativas de las siguientes incertidumbres absolutas:
- 74.1 ± 0.1 mg,
- 3.2914 ± 0.1 mg.
Solución
- \[\dfrac{0.2\, mg}{74.1\, mg} = 0.0027\, \text{or} \, 0.003 \nonumber\](tenga en cuenta que el cociente es adimensional) esto puede expresarse como 0.3% (3 partes por cien) o 3 partes por mil.
- \[\dfrac{0.0002 \,g}{3.2913\, g} = 8.4 \times 10^{-5} \, \text{or roughly} \,8 \times 10^{-5} \nonumber\], que podemos expresar como\(8 \times 10^{-3}\%\) (0.008 partes por cien), o (8E—5/10) = 8E—6 = 8 PPM.
Las incertidumbres relativas son ampliamente utilizadas para expresar la confiabilidad de las mediciones, incluso las de una sola observación, en cuyo caso la incertidumbre es la del dispositivo de medición. Las incertidumbres relativas se pueden expresar como partes por cien (por ciento), por mil (PPT), por millón, (PPM), y así sucesivamente.
Propagación del error
A menudo se nos llama a encontrar el valor de alguna cantidad cuya determinación depende de varios otros valores medidos, cada uno de los cuales está sujeto a sus propias fuentes de error.
Considera un experimento común de laboratorio en el que debes determinar el porcentaje de ácido en una muestra de vinagre observando el volumen de solución de hidróxido de sodio requerido para neutralizar un volumen dado del vinagre. Se lleva a cabo el experimento y se obtiene un valor. Solo para estar en el lado seguro, repites el procedimiento en otra muestra idéntica de la misma botella de vinagre. Si realmente lo has hecho en el laboratorio, sabrás que es muy poco probable que el segundo ensayo produzca el mismo resultado que el primero. De hecho, si ejecutas una serie de determinaciones replicadas (es decir, idénticas en todos los sentidos), probablemente obtengas una dispersión de resultados.
Para entender por qué, considera todas las medidas individuales que van en cada determinación; el volumen de la muestra de vinagre, su juicio sobre el punto en el que se neutraliza el vinagre, y el volumen de solución utilizada para llegar a este punto. Y con qué precisión conoce la concentración de la solución de hidróxido de sodio, que se conformó disolviendo un peso medido del sólido en agua y luego agregando más agua hasta que la solución alcance algún volumen medido. Cada una de estas muchas observaciones está sujeta a errores aleatorios; debido a que tales errores son aleatorios, ocasionalmente pueden cancelarse, pero para la mayoría de los ensayos no tendremos tanta suerte —de ahí la dispersión en los resultados.
Reglas para estimar errores en resultados calculados
Supongamos que mide la masa y el volumen de una muestra, y se requiere calcular su densidad dividiendo una cantidad por la otra: d = m/V. Ambos componentes de este cociente tienen incertidumbres asociadas a ellos, y se desea adjuntar una incertidumbre a la densidad calculada. El problema general de determinar la incertidumbre de un resultado calculado resulta ser bastante más complicado de lo que piensas, y no será tratado aquí. Hay, sin embargo, algunas reglas muy simples que son suficientes para la mayoría de los propósitos prácticos.
- Suma y resta, ambos números tienen incertidumbres: El método más simple es simplemente sumar las incertidumbres absolutas.
- Multiplicación o división, ambos números tienen incertidumbres: Convertir las incertidumbres absolutas en incertidumbres relativas, y sumarlas. O mejor, sumar sus cuadrados y tomar la raíz cuadrada de la suma.
- Multiplicación o división por un número puro: Caso trivial; multiplicar o dividir la incertidumbre por el número puro.
\[(6.3 ± 0.05 cm) – (2.1 ± 0.05 cm) = 4.2 ± 0.10 cm\]
No obstante, esto tiende a sobreestimar la incertidumbre asumiendo el peor caso posible en el que el error en una de las cantidades está en su valor máximo positivo, mientras que el de la otra cantidad está en su valor mínimo máximo.
La teoría estadística nos informa que un valor más realista para la incertidumbre de una suma o diferencia es sumar los cuadrados de cada incertidumbre absoluta, para luego tomar la raíz cuadrada de esta suma. Aplicando esto a los valores anteriores, tenemos
\[\sqrt{(0.05)^2 + (0.05)^2} = 0.07\]
por lo que el resultado es 4.2 ± 0.07 cm.
Estimar el error absoluto en la densidad calculada dividiendo (12.7 ± .05 g) por (10.0 ± 0.02 mL).
Solución
Incertidumbre relativa de la masa:
\[\dfrac{0.05}{12.7} = 0.0039 = 0.39\% \nonumber\]
Incertidumbre relativa del volumen:
\[\dfrac{0.02}{10.0} = 0.002 = 0.2\% \nonumber\]
Incertidumbre relativa de la densidad:
\[ \sqrt{ (0.39)^2 + (0.2)^2} = 0.44 \% \nonumber\]
Masa ÷ volumen:
\[(12.7\, g) ÷ (10.0 \,mL) = 1.27 \,g \,mL^{–1} \nonumber \]
Incertidumbre absoluta de la densidad:
\[(± 0.044) \times (1.27 \,g \,mL^{–1}) = ±0.06\, g\, mL^{–1} \nonumber \]


