11.5: Cálculos de Equilibrio
- Page ID
- 70679
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los cinco ejemplos presentados anteriormente fueron cuidadosamente seleccionados para abarcar la gama de tipos de problemas que se espera que puedan enfrentar los estudiantes matriculados en cursos universitarios de química de primer año. Si eres capaz de reproducir estas soluciones por tu cuenta, debes estar bien preparado sobre este tema.
- El primer paso en la solución de todos los problemas de equilibrio excepto los más simples es esbozar una tabla que muestre para cada componente la concentración o presión inicial, el cambio en esta cantidad (por ejemplo, +2 x), y los valores de equilibrio (por ejemplo,. 0036 + 2 x). Al hacerlo, la secuencia de cálculos requeridos para llegar a la respuesta suele hacerse evidente.
- Los cálculos de equilibrio a menudo implican ecuaciones cuadráticas o de orden superior. Debido a que las concentraciones, presiones y constantes de equilibrio rara vez se conocen con una precisión de más de unas pocas cifras significativas, no hay necesidad de buscar soluciones exactas. Las aproximaciones iterativas (como en Ejemplo\(\PageIndex{3}\)) o el uso de una calculadora gráfica (Ejemplo\(\PageIndex{4}\)) son adecuadas y convenientes.
- Los equilibrios de distribución de fases juegan un papel importante en los procesos de separación química tanto a escala industrial como de laboratorio. También están involucrados en el movimiento de químicos entre diferentes partes del ambiente, y en la bioconcentración de contaminantes en la cadena alimentaria.
Esta página presenta ejemplos que cubren la mayoría de los tipos de problemas de equilibrio que es probable que encuentre en un curso universitario de primer año. ¡Al leer esta página no te enseñará a trabajar los problemas de equilibrio! El único que puede enseñarte a interpretar, entender y resolver problemas eres tú mismo. Así que no te limites a “leer” esto y pensar que ya has terminado. Necesitas encontrar y resolver problemas similares por tu cuenta. Observe los problemas en su tarea de tarea o al final del capítulo correspondiente en un libro de texto, y vea cómo encajan en los tipos generales que se describen a continuación. Cuando puedas resolverlos sin mirar los ejemplos a continuación, ¡estarás bien en camino!
Cálculo de constantes de equilibrio
Claramente, si se conocen las concentraciones o presiones de todos los componentes de una reacción, entonces el valor de se\(K\) puede encontrar por simple sustitución. Sin embargo, observar concentraciones individuales o presiones parciales directamente puede no ser siempre práctico. Si uno de los componentes está coloreado, la medida en que absorbe luz de una longitud de onda apropiada puede servir como índice de su concentración. Las mediciones de presión son normalmente capaces de medir solo la presión total de una mezcla gaseosa, por lo que si dos o más productos gaseosos están presentes en la mezcla de equilibrio, la presión parcial de uno puede necesitar inferirse de la del otro, tomando en cuenta la estequiometría de la reacción.
En un experimento realizado por Taylor y Krist (J. Am. Chem. Soc. 1941:1377), se encontró que el yoduro de hidrógeno estaba 22.3% disociado a 730.8 K. Calcular\(K_c\) para
\[\ce{ 2 HI(g) <=> H2(g) + I2} \nonumber \]
Solución
No se dan concentraciones molares explícitas, pero sí sabemos que por cada\(n\) mol de\(\ce{HI}\), se forman\(0.223n\) moles de cada producto y\((1–0.223)n = 0.777n\) moles de\(\ce{HI}\) restos. Por simplicidad, asumimos que\(n=1\) y que la reacción se lleva a cabo en un recipiente de 1.00-L, de manera que podemos sustituir los términos de concentración requeridos directamente en la expresión de equilibrio para\(K_c\).
\[\begin{align*} K_c &= \dfrac{[\ce{H2}][\ce{I2}]}{[\ce{HI}]^2} \\[4pt] &= \dfrac{(0.223)(0.223)}{(0.777)^2} \\[4pt] &= 0.082 \end{align*}\]
El fósforo blanco ordinario,\(\ce{P4}\), forma un vapor que se disocia en moléculas diatómicas a altas temperaturas:
\[\ce{P4(g) <=> 2 P2(g)} \nonumber\]
Una muestra de fósforo blanco, cuando se calentó a 1000°C, formó un vapor con una presión total de 0.20 atm y una densidad de 0.152 g L —1. Utilice esta información para evaluar la constante de equilibrio\(K_p\) para esta reacción.
Solución
Antes de preocuparse por lo que tiene que ver la densidad de la mezcla de gases\(K_p\), comience de la manera habitual estableciendo la información requerida para expresar\(K_p\) en términos de un desconocido\(x\)
| Mesa ICE | \(P_{4(g)}\) | \(P_{2(g)}\) | comentar |
|---|---|---|---|
| I nitial (moles) | \ (P_ {4 (g)}\)” style="text-align:center; vertical-align:middle; ">1 | \ (P_ {2 (g)}\)” style="vertical-align:middle; ">0 | Dado que\(K\) es independiente del número de moles, asuma el caso inicial más simple. |
| C hange (moles) | \ (P_ {4 (g)}\)” style="text-align:center; vertical-align:middle; ">\(-x\) | \ (P_ {2 (g)}\)” style="vertical-align:middle; ">\(2x\) | x es la fracción de P 4 que se disocia. |
| E quilibrium (moles) | \ (P_ {4 (g)}\)” style="text-align:center; vertical-align:middle; ">\(1-x\) | \ (P_ {2 (g)}\)” style="text-align:center; vertical-align:middle; ">\(2x\) | El denominador es el número total de moles: |
| Fracción molar | \ (P_ {4 (g)}\)” style="text-align:center; vertical-align:middle; ">\(\chi_{P_4}=\dfrac{1-x}{1+x}\) | \ (P_ {2 (g)}\)” style="text-align:center; vertical-align:middle; ">\(\chi_{P_2}=\dfrac{2x}{1+x}\) | El denominador es el número total de moles: |
| Equilibrio (presiones) |
\ (P_ {4 (g)}\)” style="text-align:center; vertical-align:middle; ">\(p_{P_4} = \chi_{P_4} 0.2 = \left( \dfrac{1-x}{1+x}\right) 0.2 \) | \ (P_ {2 (g)}\)” style="text-align:center; vertical-align:middle; ">\(p_{P_2} = \chi_{P_2} 0.2 = \left( \dfrac{2x}{1+x}\right) 0.2 \) | La presión parcial es la fracción molar multiplicada por la presión total. |
Las presiones parciales en la fila inferior se encontraron multiplicando la fracción molar de cada gas por la presión total:
\[P_i = \chi_i P_{tot} \nonumber\]
con el término en el denominador de cada fracción molar es el número total de moles de gas presentes en equilibrio:
\[P_{tot} = 1-x + 2x = 1+x \nonumber\]
Expresando la constante de equilibrio en términos de\(x\) da
\[ \begin{align*} K_p &= \dfrac{p^2_{P_2}}{p_{P_4}} \\[4pt] &= \dfrac{\left(\dfrac{2x}{1+x}\right)^2 0.2^2} {\left(\dfrac{1-x}{1+x}\right) 0.2} \\[4pt] &= \left(\dfrac{4x^2}{(1-x)(1+x)}\right) 0.2 \\[4pt] &= \left(\dfrac{4x^2}{1+x^2}\right) 0.2 \end{align*}\]
Ahora necesitamos encontrar la fracción\(x\) de disociación de\(P_4\), y en este punto esperamos que recuerdes esas leyes de gas que te dijeron que necesitarías más adelante en el curso! La densidad de un gas es directamente proporcional a su peso molecular, por lo que es necesario calcular las densidades de\(P_2\) vapores puros\(P_4\) y puros bajo las condiciones del experimento. Una de estas densidades será mayor a 0.152 gL —1 y la otra será menor; todo lo que necesitas hacer es encontrar dónde cae la densidad medida entre los dos límites, y tendrás la fracción de disociación.
El peso molecular del fósforo es de 31.97, dando una masa molar de 127.9 g para\(\ce{P4}\). Esta masa debe dividirse por el volumen para encontrar la densidad; asumiendo el comportamiento ideal del gas, el volumen de 127.9 g (1 mol) de\(\ce{P4}\) está dado por RT/P, que funciona a 522 L (recuerde usar la temperatura absoluta aquí.) La densidad del\(\ce{P4}\) vapor puro bajo las condiciones del experimento es entonces
\[\rho = \dfrac{m}{V} = (128\; g \;mol^{–1}) \times x = (522\; L mol^{–1}) = 0.245\; g\; L^{–1} \nonumber\]
La densidad de puro\(P_2\) sería la mitad de esta, o 0.122 g L —1. La diferencia entre estas dos densidades limitantes es de 0.123 g L —1, y la diferencia entre la densidad de puro\(\ce{P4}\) y la de la mezcla de equilibrio es de (0.245 — 0.152) g L —1 o 0.093 g L —1. La relación 0.093/0.123 = 0.76 es por lo tanto la fracción de\(\ce{P4}\) que queda y su disociación fraccional es (1 — 0.76) = 0.24. Sustituir en la expresión de equilibrio anterior da\(K_p = 1.2\).
Resolver Ejemplo\(\PageIndex{2}\) mediante el uso de un conjunto diferente de condiciones iniciales para demostrar que las condiciones iniciales de hecho no tienen ningún efecto en la determinación del estado de Equilibrio y\(K_p\).
Cálculo de concentraciones de equilibrio
Este es, con mucho, el tipo de problema de equilibrio más común que encontrarás: comenzando con un número arbitrario de moles de cada componente, ¿cuántos moles de cada uno estarán presentes cuando el sistema llegue al equilibrio? La principal fuente de confusión y error para los principiantes se relaciona con la necesidad de determinar los valores de varias incógnitas (una concentración o presión para cada componente) a partir de una sola ecuación, la expresión de equilibrio. La clave de esto es hacer uso de las relaciones estequiométricas entre los diversos componentes, que generalmente nos permiten expresar la composición de equilibrio en términos de una sola variable. La forma más fácil y libre de errores de hacerlo es adoptar un enfoque sistemático en el que se crea y rellena una pequeña tabla como se muestra en el siguiente ejemplo de problema. Luego sustituyes los valores de equilibrio en la expresión constante de equilibrio, y la resuelves por lo desconocido.
Esto muy a menudo implica resolver una ecuación cuadrática o de orden superior. Por supuesto, las cuadráticas se pueden resolver usando la fórmula cuadrática familiar, pero a menudo es más fácil usar una aproximación algebraica o gráfica, y para ecuaciones de orden superior este es el único enfoque práctico. Casi nunca hay necesidad de obtener una respuesta exacta, ya que las constantes de equilibrio con las que empiezas rara vez se conocen todo eso precisamente de todos modos.
El fosgeno (\(\ce{COCl2}\)) es un gas venenoso que se disocia a alta temperatura en otros dos gases venenosos, el monóxido de carbono y el cloro. La constante de equilibrio K p = 0.0041 a 600°K. Encontrar la composición de equilibrio del sistema después de 0.124 atm de\(\ce{COCl2}\) se permite alcanzar el equilibrio a esta temperatura.
Solución
Primero necesitamos una reacción química equilibrada
\[\ce{COCl_2 <=> CO(g) + Cl2(g)} \nonumber\]
Comience dibujando una tabla que muestre las relaciones entre los componentes:
| Mesa ICE | \(COCl_2\) | \(CO_{(g)}\) | \(Cl_{2(g)}\) |
|---|---|---|---|
| I nitial (presión) | \ (COCL_2\)” style="text-align:center; ">0.124 atm | \ (CO_ {(g)}\)” style="text-align:center; ">0 | \ (Cl_ {2 (g)}\)” style="text-align:center; ">0 |
| C hange (presión) | \ (COCL_2\)” style="text-align:center; ">-x | \ (CO_ {(g)}\)” style="text-align:center; ">+x | \ (Cl_ {2 (g)}\)” style="text-align:center; ">+x |
| E quilibrium (presión) | \ (COCL_2\)” style="text-align:center; ">0.124 — x | \ (CO_ {(g)}\)” style="text-align:center; ">+x | \ (Cl_ {2 (g)}\)” style="text-align:center; ">+x |
La sustitución de las presiones de equilibrio en la expresión de equilibrio da
\[ \dfrac{x^2}{0.124 - x} = 0.0041 \nonumber\]
Esta expresión se puede reorganizar en forma polinómica estándar
\[x^2 +0.0041 x – 0.00054 = 0 \nonumber\]
y resuelto por la fórmula cuadrática, pero simplemente obtendremos una solución aproximada por iteración. Debido a que la constante de equilibrio es pequeña, sabemos que x será bastante pequeña en comparación con 0.124, por lo que la relación anterior puede aproximarse por
\[ \dfrac{x^2}{0.124 - x} \approx \dfrac{x^2}{0.124}= 0.0041 \nonumber\]
lo que da x = 0.0225. Para ver lo bueno que es esto, sustituya este valor de x en el denominador de la ecuación original y resuelva de nuevo:
\[ \dfrac{x^2}{0.124 - 0.0225} = \dfrac{x^2}{0.102}= 0.0041 \nonumber\]
Esta vez, resolviendo para\(x\) da 0.0204. Iterando una vez más, obtenemos
\[ \dfrac{x^2}{0.124 - 0.0204} = \dfrac{x^2}{0.104}= 0.0041 \nonumber\]
y x = 0.0206 que está suficientemente cerca del anterior para ser considerado el resultado final. Las presiones parciales finales son entonces 0.104 atm para CoCl 2, y 0.0206 atm cada una para CO y Cl 2.
Comentario: El uso de la fórmula cuadrática para encontrar la solución exacta produce las dos raíces —0.0247 (que ignoramos) y 0.0206, que muestran que nuestra aproximación es bastante buena.
La disociación en fase gaseosa del pentacloruro de fósforo al tricloruro tiene\(K_p = 3.60\) a 540°C:
\[\ce{PCl5(g) <=> PCl3(g) + Cl2(g)} \nonumber\]
¿Cuáles serán las presiones parciales de los tres componentes si\(\ce{PCl3}\) se combinan 0.200 moles\(\ce{PCl5}\) y 3.00 moles de y se ponen en equilibrio a esta temperatura y a una presión total de 1.00 atm?
Solución
Como siempre, configura una tabla que muestre lo que sabes (las dos primeras filas) y luego expresando las cantidades de equilibrio:
| Mesa ICE | \(\ce{PC5(g)}\) | \(\ce{PCl3(g)}\) | \(\ce{Cl2(g)}\) |
|---|---|---|---|
| Inicial (moles) | \ (\ ce {PC5 (g)}\)” style="text-align:center; ">0.200 | \ (\ ce {PCL3 (g)}\)” style="text-align:center; ">3.00 | \ (\ ce {Cl2 (g)}\)” style="text-align:center; ">0 |
| Cambio (moles) | \ (\ ce {PC5 (g)}\)” style="text-align:center; ">—x | \ (\ ce {PCL3 (g)}\)” style="text-align:center; ">+x | \ (\ ce {Cl2 (g)}\)” style="text-align:center; ">+x |
| Equilibrio (moles) | \ (\ ce {PC5 (g)}\)” style="text-align:center; ">0.200 — x | \ (\ ce {PCL3 (g)}\)” style="text-align:center; ">3.00 + x | \ (\ ce {Cl2 (g)}\)” style="text-align:center; ">x |
| Equilibrio (presiones parciales) | \ (\ ce {PC5 (g)}\)” style="text-align:center; ">\(\dfrac{2.00 - x }{ 3.20 + x}\) | \ (\ ce {PCL3 (g)}\)” style="text-align:center; ">\(\dfrac{3.00 + x }{ 3.20 + x}\) | \ (\ ce {Cl2 (g)}\)” style="text-align:center; ">\(\dfrac{ x }{ 3.20 + x}\) |
Las presiones parciales en la fila inferior se encontraron multiplicando la fracción molar de cada gas por la presión total:
\[P_i = \chi_i P_{tot} \nonumber\]
con el término en el denominador de cada fracción molar es el número total de moles de gas presentes en equilibrio:
\[P_{tot} = (0.200 – x) + (3.00 + x) + x = 3.20 + x \nonumber\]
Sustituyendo las presiones parciales de equilibrio en la expresión de equilibrio, tenemos
\[ \dfrac{ (3.00 +x)(x)}{(0.200 -x)(3.20 +x)} = 3.60 \nonumber\]
cuya forma polinómica es
\[4.60x^2 + 13.80x – 2.304 = 0. \nonumber\]
Puedes usar la pregunta cuadrática para resolver esto o puedes hacerlo gráficamente (más útil para ecuaciones de orden superior). Al trazar esto en una calculadora gráfica\(x = 0.159\) se obtiene como raíz positiva:
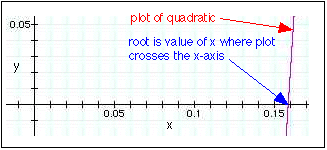
La sustitución de esta raíz en las expresiones para las presiones parciales de equilibrio en la tabla produce los siguientes valores:
- \(P_{\ce{PCl5}}\)= 0.012 atm,
- \(P_{\ce{PCl3}}\)= 0.94 atm,
- \(P_{\ce{Cl2}}\)= 0.047 atm.
Efectos de la dilución sobre el equilibrio
En la sección que introdujo el principio de Le Chatelier, se mencionó que diluir un ácido débil como el ácido acético\(\ce{CH3COOH}\) (“\(\ce{HAc}\)”) desplazará el equilibrio de disociación hacia la derecha:
\[\ce{HAc + H_2O \rightleftharpoons H_3O^{+} + Ac^{–}} \nonumber\]
Así una\(0.10\,M\) solución de ácido acético se ioniza 1.3%, mientras que en una solución 0.01 M, 4.3% de las\(\ce{HAc}\) moléculas se disociarán. Esto se debe a que a medida que la solución se diluye más, el producto [H 3 O +] [Ac —] disminuye más rápidamente que el\(\ce{[HAc]}\) término. Al mismo tiempo la concentración de\(\ce{H2O}\) se vuelve mayor, pero debido a que es tan grande para empezar (alrededor de 55.5 M), cualquier efecto que esto pueda tener es despreciable, razón por la cual ningún\(\ce{[H2O]}\) término aparece en la expresión de equilibrio.
Para una reacción como
\[\ce{CH_3COOH (l) + C_2H_5OH (l) \rightleftharpoons CH_3COOC_2H_5 (l) + H_2O (l) }\]
(en la que la concentración de agua sí cambia), la dilución no tendrá ningún efecto sobre el equilibrio; la situación es análoga a la forma en que la dependencia de la presión de una reacción en fase gaseosa depende del número de moles de componentes gaseosos a cada lado de la ecuación (i.e.,\(\Delta n_g\)).
La formación bioquímica de un azúcar disacárido (doble) a partir de dos monosacáridos se ejemplifica por la reacción
\[\text{fructose} (aq) + \text{glucose-6-phosphate} (aq) → \text{sucrose-6-phosphate} (aq) + \ce{H2O} (l)\]
(La sacarosa es el azúcar de mesa ordinario.) ¿A qué volumen se debe diluir una solución que contenga 0.050 mol de cada monosacárido para lograr una conversión del 5% a fosfato de sacarosa? La constante de equilibrio para esta reacción es\(K_{c} = 7.1 \times 10^{-6}\) a temperatura ambiente.
Solución
Los números iniciales y finales de moles en esta ecuación son los siguientes:
| Mesa ICE | fructosa (\(\text{fruc}\)) | Glucosa-6-P (\(\text{gluc6P}\)) | Sacarosa-6-P (\(\text{suc6P}\)) | agua\( \ce{H2O}\)) |
|---|---|---|---|---|
| I nitial (moles) | \ (\ text {fruc}\))” style="vertical-align:middle; ">0.05 | \ (\ text {gluc6p}\))” style="vertical-align:middle; ">0.05 | \ (\ text {Suc6p}\))” style="vertical-align:middle; ">0 | \ (\ ce {H2O}\))” style="vertical-align:middle; ">- |
| C hange (moles) | \ (\ text {fruc}\))” style="vertical-align:middle; ">-x | \ (\ text {gluc6p}\))” style="vertical-align:middle; ">-x | \ (\ text {Suc6p}\))” style="text-align:center; vertical-align:middle; ">+x | \ (\ ce {H2O}\))” style="text-align:center; vertical-align:middle; ">- |
| E quilibrium (moles) | \ (\ text {fruc}\))” style="vertical-align:middle; ">0.05-x | \ (\ text {gluc6p}\))” style="vertical-align:middle; ">0.05-x | \ (\ text {Suc6p}\))” style="text-align:center; vertical-align:middle; ">+x | \ (\ ce {H2O}\))” style="text-align:center; vertical-align:middle; ">- |
¿Cuál es el valor de\(x\)? Es decir, cuando ha procedido el 5% de la reacción o cuando se consume el 5% de la fructosa (o glucosa-6-P):
\[\dfrac{x}{0.05} = 0.05 \nonumber\]
así\(x = 0.0025 \nonumber\). Las concentraciones equilibradas son entonces
- \([\text{suc6P}]_{equil} = \dfrac{0.0025}{V}\)
- \([\text{fruc}]_{equil} = \dfrac{0.0475}{V}\)
- \([\text{glu6P}]_{equil} = \dfrac{0.0475}{V}\)
Sustituyendo en los valores en para la expresión de\(K_c\) (en la que el volumen de solución es el desconocido), tenemos
\[\begin{align*} K_{c} &= \dfrac{[\text{suc6P}]_{equil} }{[\text{fruc}]_{equil} [\text{gluc6P}]_{equil} } \\[4pt] &= \dfrac{\left(\dfrac{0.0025}{V}\right)}{\left(\dfrac{0.0475}{V}\right)^2} = 7.1 \times 10^{-6} \end{align*}\]
\[V = (7.1 \times 10^{-6}) \dfrac{(0.0475)^2}{0.0025} \nonumber\]
Resolviendo para\(V\) da un volumen de solución final de\(6.4 \times 10^{-4}\,L\) o\(640 \mu L\). ¿Por qué tan pequeño? La reacción no se ve favorecida y para empujarla hacia adelante, se necesitan grandes concentraciones de reactivos (principio de Le Chatelier en acción).


