11.3: Cociente de reacción
- Page ID
- 70680
Asegúrese de comprender a fondo las siguientes ideas esenciales:
- Cuando se combinan cantidades arbitrarias de los diferentes componentes de un sistema de reacción química, la composición general del sistema probablemente no corresponderá a la composición de equilibrio. Como resultado, un cambio neto en la composición (“un desplazamiento hacia la derecha o hacia la izquierda”) tenderá a tener lugar hasta que se alcance el estado de equilibrio.
- El estado del sistema de reacción con respecto a su estado de equilibrio se caracteriza por el valor de la expresión de equilibrio cuya formulación se define por los coeficientes en la ecuación de reacción equilibrada; puede expresarse en términos de concentraciones, o en el caso de componentes gaseosos, como presiones parciales.
- Los diversos términos en la expresión de equilibrio pueden tener cualquier valor arbitrario (incluyendo cero); el valor de la expresión de equilibrio en sí se llama cociente de reacción Q.
- Si los términos de concentración o presión en la expresión de equilibrio corresponden al estado de equilibrio del sistema, entonces Q tiene el valor especial K, que llamamos la constante de equilibrio.
- La relación Q/K (ya sea 1, >1 o <1) sirve así como un índice de lo lejos que está el sistema de su composición de equilibrio, y su valor indica la dirección en la que debe proceder la reacción neta para alcanzar su estado de equilibrio.
- Cuando Q = K, entonces se ha alcanzado el estado de equilibrio, y no se producirá ningún cambio neto adicional en la composición mientras el sistema permanezca intacto.
Considera una reacción simple como la síntesis en fase gaseosa de yoduro de hidrógeno a partir de sus elementos:\[H_2 + I_2 \rightarrow 2 HI\] Supongamos que combina cantidades arbitrarias de\(H_2\),\(I_2\) y\(HI\). ¿La reacción creará más HI, o se consumirá parte del HI a medida que el sistema se mueva hacia su estado de equilibrio? El concepto del cociente de reacción, que es el foco de esta breve lección, facilita predecir lo que sucederá.
¿Qué es el cociente de equilibrio?
En la sección anterior definimos la expresión de equilibrio para la reacción
En el caso general en el que las concentraciones pueden tener valores arbitrarios (incluyendo cero), esta expresión se denomina cociente de reacción (también se usa comúnmente el término cociente de equilibrio.) y su valor se denota por\(Q\) (\(Q_c\)o\(Q_p\) si deseamos enfatizan que los términos representan concentraciones molares o presiones parciales). Si los términos corresponden a concentraciones de equilibrio, entonces la expresión anterior se llama la constante de equilibrio y su valor se denota por\(K\) (o\(K_c\) o\(K_p\)).
\(K\)es así el valor especial que\(Q\) tiene cuando la reacción está en equilibrio
El valor de Q en relación con K sirve como índice de cómo se compara la composición del sistema de reacción con la del estado de equilibrio, y así indica la dirección en la que debe proceder cualquier reacción neta. Por ejemplo, si combinamos los dos reactivos A y B a concentraciones de 1 mol L —1 cada uno, el valor de Q será 0÷1=0. El único cambio posible es la conversión de algunos de estos reactivos en productos. Si en cambio nuestra mezcla consiste únicamente en los dos productos C y D, Q será indeterminadamente grande (1÷0) y el único cambio posible será en sentido inverso.
Por ejemplo, si combinamos los dos reactivos A y B a concentraciones de 1 mol L —1 cada uno, el valor de Q será 0÷1=0. El único cambio posible es la conversión de algunos de estos reactivos en productos. Si en cambio nuestra mezcla consiste únicamente en los dos productos C y D, Q será indeterminadamente grande (1÷0) y el único cambio posible será en sentido inverso.
Es fácil ver (por simple aplicación del principio Le Chatelier) que la relación Q/K inmediatamente nos dice si, y en qué dirección, se producirá una reacción neta a medida que el sistema se mueva hacia su estado de equilibrio. A continuación se muestra una vista esquemática de esta relación:
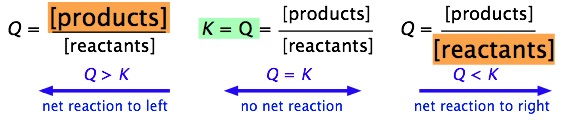
Es muy importante que seas capaz de elaborar estas relaciones por ti mismo, no memorizándolas, sino a partir de las definiciones de\(Q\) y\(K\).
| Condición | Estado del Sistema |
|---|---|
| Q > K | Concentración del producto demasiado alta para el equilibrio; la reacción neta procede a la izquierda. |
| Q = K | El sistema está en equilibrio; no se producirá ningún cambio neto. |
| Q < K | Concentración del producto demasiado baja para el equilibrio; la reacción neta procede a la derecha. |
Es muy importante que seas capaz de elaborar estas relaciones por ti mismo, no memorizándolas, sino a partir de las definiciones de\(Q\) y\(K\).
La constante de equilibrio para la oxidación del dióxido de azufre es K p = 0.14 a 900 K.
\[\ce{2 SO_2(g) + O_2(g) \rightleftharpoons 2 SO_3(g)} \nonumber\]
Si un recipiente de reacción se llena con SO 3 a una presión parcial de 0.10 atm y con O 2 y SO 2 cada uno a una presión parcial de 0.20 atm, ¿qué se puede concluir sobre si, y en qué dirección, se producirá algún cambio neto en la composición?
Solución:
El valor del cociente de equilibrio Q para las condiciones iniciales es
\[ Q= \dfrac{p_{SO_3}^2}{p_{O_2}p_{SO_2}^2} = \dfrac{(0.10\; atm)^2}{(0.20 \;atm) (0.20 \; atm)^2} = 1.25\; atm^{-1} \nonumber\]
Desde Q > K, la reacción no está en equilibrio, por lo que se producirá un cambio neto en una dirección que disminuya Q. Esto solo puede ocurrir si parte del SO 3 se vuelve a convertir en productos. Es decir, la reacción “se desplazará hacia la izquierda”.
Las definiciones formales de Q y K son bastante simples, pero son de utilidad limitada a menos que seas capaz de relacionarlas con situaciones químicas reales. Los siguientes diagramas ilustran la relación entre Q y K desde diversos puntos de vista. Tómate un tiempo para estudiar cada uno con cuidado, asegurándote de que eres capaz de relacionar la descripción con la ilustración.
Para la reacción
\[N_2O_{4(g)} \rightleftharpoons 2 NO_{2(g)} \nonumber\]
K c = 0.0059 a 298 K.
Esta condición de equilibrio está representada por la curva roja que pasa por todos los puntos de la gráfica que satisfacen el requisito de que
\[Q = \dfrac{[NO_2]^2}{ [N_2O_4]} = 0.0059 \nonumber\]
Por supuesto, hay un número infinito de Q posibles de este sistema dentro de los límites de concentración mostrados en la gráfica. Sólo aquellos puntos que caen sobre la línea roja corresponden a estados de equilibrio de este sistema (aquellos para los cuales\(Q = K_c\)). La línea en sí es una gráfica de [NO 2] que obtenemos reordenando la expresión de equilibrio
\[[NO_2] = \sqrt{[N_2O_4]K_c} \nonumber\]
Si el sistema se encuentra inicialmente en un estado de no equilibrio, su composición tenderá a cambiar en una dirección que lo mueva a uno que está en la línea. Se muestran dos estados de no equilibrio de este tipo. El estado indicado por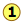
has\(Q > K\), por lo que esperaríamos una reacción neta que reduzca Q al convertir parte del NO 2 en N 2 O 4; es decir, el equilibrio “se desplaza hacia la izquierda”. De igual manera, en estado
, Q < K, lo que indica que se producirá la reacción directa.
Las flechas azules en el diagrama anterior indican los valores sucesivos que Q asume a medida que la reacción se acerca al equilibrio. La pendiente de la línea refleja la estequiometría de la ecuación. En este caso, un mol de reactivo produce dos moles de productos, por lo que las pendientes tienen un valor absoluto de 2:1.
Uno de los equilibrios más simples que podemos escribir es el que hay entre un sólido y su vapor. En este caso, la constante de equilibrio es solo la presión de vapor del sólido. Así para el proceso
\[I_{2(s)} \rightleftharpoons I_{2(g)} \nonumber\]
todos los estados de equilibrio posibles del sistema se encuentran en la línea roja horizontal y son independientes de la cantidad de sólidos presentes (siempre y cuando haya al menos lo suficiente para suministrar la pequeña cantidad relativa de vapor).
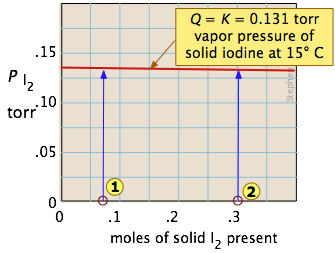
Por lo que agregar varias cantidades del sólido a un recipiente cerrado vacío (estados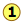 y) provoca una acumulación gradual de vapor de yodo. Debido a que la presión de equilibrio del vapor es tan pequeña, la cantidad de sólidos consumidos en el proceso es insignificante, por lo que las flechas van hacia arriba y todas conducen a la misma presión de vapor de equilibrio.
La descomposición del cloruro amónico es un ejemplo común de equilibrio heterogéneo (bifásico). El cloruro de amonio sólido tiene una presión de vapor sustancial incluso a temperatura ambiente:
\[NH_4Cl_{(s)} \rightleftharpoons NH_{3(g)} + HCl_{(g)}\]
Flecha traza los estados por los que pasa el sistema cuando se coloca NH 4 Cl sólido en un recipiente cerrado. La flecha representa la adición de amoníaco a la mezcla de equilibrio; el sistema responde siguiendo el camino de
regreso a un nuevo estado de equilibrio
que, como predice el principio de Le Chatelier, contiene una cantidad menor de amoníaco que la añadida. Las pendientes unitarias de los caminos y reflejan la estequiometría 1:1 de los productos gaseosos de la reacción.