Difusión y Derrame
- Page ID
- 74843
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para Desarrollar
- Describir las interacciones involucradas con el derrame y la difusión
En esta sección se discuten los movimientos de gases. Este es en realidad un campo muy complicado (llamado dinámica de fluidos) y no vamos a ir muy profundo.
Derrame
El derrame es el movimiento de un gas a través de un pequeño agujero hacia un vacío. Queremos saber la tasa de derrame, que es la cantidad de gas que se mueve a través del agujero por unidad de tiempo. Suponemos que las partículas de gas no chocan entre sí mientras se mueven a través del agujero (esto significa que es un agujero estrecho en una pared delgada). Entonces, la tasa de derrame solo depende de la frecuencia con la que las partículas chocan en el agujero. Esto depende de su densidad y velocidad. Debido a que a una temperatura dada, todos los gases tienen la misma energía cinética, su velocidad es inversamente proporcional a m 1/2, la raíz cuadrada de la masa. Así, las tasas relativas de derrame para diferentes gases a la misma temperatura son
\[\frac{Effusion\; rate\; for\; gas\; 1}{Effusion\; rate\; for\; gas\; 2} = \frac{M_{2}^{\frac{1}{2}}}{M_{1}^{\frac{1}{2}}}\]
donde M 1 y M 2 son los pesos moleculares del gas 1 y el gas 2.
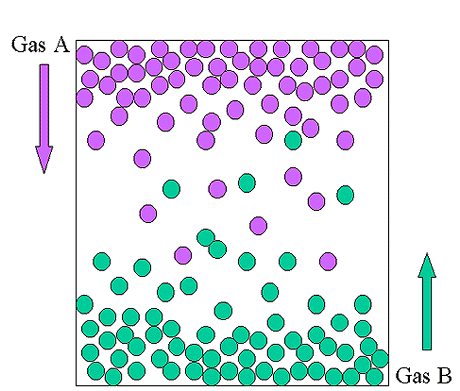
Difusión
La difusión es un proceso más complicado. Significa el movimiento de gases uno a través del otro o la difusión de un gas a través de otro. Debido a que hay muchas colisiones, los gases se mueven mucho más lento de lo que cabría esperar de las velocidades promedio cercanas a 400-700 m/s. (Es por eso que tomará un momento oler perfume cuando alguien entra en una habitación). Técnicamente, muchos procesos que suenan así no son precisamente de difusión simple. Tenemos que tener cuidado sobre si hay diferencias de presión o flujos de gases (como el viento). Si los hay entonces el proceso no es simple difusión y no seguirá perfectamente las ecuaciones para una difusión simple. (La ecuación para difusión simple es la misma que para efusión, pero por diferentes razones, ver más adelante.) Para nuestros propósitos, cuando se quiere predecir las tasas relativas de movimiento de los gases, puede comenzar con la ecuación de efusión/difusión. Será exactamente correcto en algunas situaciones, y lo suficientemente cerca en algunas otras. Las otras situaciones puedes estudiar en una clase más avanzada si te interesa.
Explicación de ecuación de difusión
¿Por qué la ecuación de difusión es la misma que la ecuación de efusión, pero por otra razón? En simple difusión, 2 gases se mueven en direcciones opuestas a través de un medio con la misma presión en todas partes. Si la presión en el medio es constante, entonces las colisiones de un gas con el medio se equilibran con las colisiones del otro gas. El impulso dado al medio por un gas en una colisión promedio es mV, donde m es la masa y V es la velocidad de difusión (que es diferente de la velocidad promedio de las partículas: es la velocidad general de movimiento del gas). El número de colisiones es proporcional a nv, donde n es el número de partículas y v es su velocidad promedio. Como no hay diferencia de presión,
\[\left(m_{1}V_{1}\right) \left(n_{1}v_{1}\right) = \left(m_{2}V_{2}\right) \left(n_{2}v_{2}\right)\]
Cuando reorganizamos, el flujo de difusión relativo (nV, cantidad de partículas que se mueven por velocidad de difusión) de los gases 1 y 2 es
\[\frac{n_{1}V_{1}}{n_{2}V_{2}} = \frac{m_{2}v_{2}}{m_{1}v_{1}}\]
Debido a que v es proporcional a m -1/2, esto nos da el mismo resultado que la ecuación de efusión. No obstante, la razón es diferente.
Enlaces externos
Colaboradores y Atribuciones
Emily V Eames (City College of San Francisco)