9.4: Derrame y Difusión de Gases

Última actualización
Guardar como PDF

Page ID: 75815

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Definir y explicar el derrame y la difusión
Ley estatal de Graham y utilizarla para calcular las propiedades relevantes del gas

Si alguna vez has estado en una habitación cuando se entregó una pizza muy caliente, te han dado cuenta de que las moléculas gaseosas pueden propagarse rápidamente por una habitación, como lo demuestra el agradable aroma que pronto llega a tu nariz. Aunque las moléculas gaseosas viajan a velocidades tremendas (cientos de metros por segundo), chocan con otras moléculas gaseosas y viajan en muchas direcciones diferentes antes de alcanzar el objetivo deseado. A temperatura ambiente, una molécula gaseosa experimentará miles de millones de colisiones por segundo. La trayectoria libre media es la distancia promedio que recorre una molécula entre colisiones. La trayectoria libre media aumenta con la presión decreciente; en general, la trayectoria libre media para una molécula gaseosa será cientos de veces el diámetro de la molécula

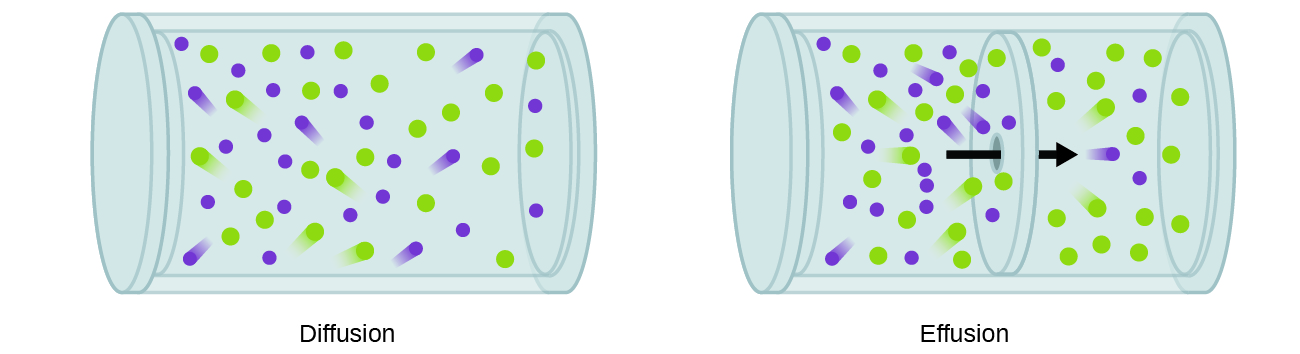
En general, sabemos que cuando se introduce una muestra de gas en una parte de un recipiente cerrado, sus moléculas se dispersan muy rápidamente por todo el contenedor; este proceso por el cual las moléculas se dispersan en el espacio en respuesta a diferencias de concentración se denomina difusión (se muestra en la Figura\(\PageIndex{1}\)) . Los átomos o moléculas gaseosas son, por supuesto, inconscientes de cualquier gradiente de concentración, simplemente se mueven aleatoriamente; las regiones de mayor concentración tienen más partículas que regiones de concentraciones más bajas, y así se produce un movimiento neto de especies de áreas de concentración alta a baja. En un ambiente cerrado, la difusión resultará en última instancia en concentraciones iguales de gas a lo largo, como se representa en la Figura\(\PageIndex{1}\). Los átomos gaseosos y las moléculas siguen moviéndose, pero como sus concentraciones son las mismas en ambos bulbos, las velocidades de transferencia entre los bulbos son iguales (no se produce una transferencia neta de moléculas).

Figura\(\PageIndex{1}\): (a) Dos gases, H ₂ y O ₂, se separan inicialmente. b) Cuando se abre la llave de paso, se mezclan. El gas más ligero, H ₂, pasa a través de la abertura más rápido que O ₂, por lo que justo después de que se abre la llave de paso, más moléculas H ₂ se mueven hacia el lado O ₂ que las moléculas O ₂ se mueven hacia el lado H ₂. (c) Al cabo de poco tiempo, tanto las moléculas O ₂ de movimiento más lento como las moléculas H ₂ de movimiento más rápido se han distribuido uniformemente en ambos lados del vaso.

A menudo nos interesa la velocidad de difusión, la cantidad de gas que pasa por alguna área por unidad de tiempo:

\[\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}} \nonumber \]

La velocidad de difusión depende de varios factores: el gradiente de concentración (el aumento o disminución de la concentración de un punto a otro); la cantidad de superficie disponible para difusión; y la distancia que deben recorrer las partículas de gas. Obsérvese también que el tiempo requerido para que ocurra la difusión es inversamente proporcional a la velocidad de difusión, como se muestra en la ecuación de velocidad de difusión.

Un proceso que implica el movimiento de especies gaseosas similar a la difusión es el derrame, el escape de moléculas de gas a través de un pequeño agujero como un agujero de alfiler en un globo hacia un vacío (Figura\(\PageIndex{1}\)). Aunque las tasas de difusión y derrame dependen de la masa molar del gas involucrado, sus tasas no son iguales; sin embargo, las proporciones de sus tasas son las mismas.

Figura\(\PageIndex{2}\): La difusión ocurre cuando las moléculas de gas se dispersan por todo un contenedor. El derrame ocurre cuando un gas pasa a través de una abertura que es menor que la trayectoria libre media de las partículas, es decir, la distancia promedio recorrida entre colisiones. Efectivamente, esto significa que solo pasa una partícula a la vez.

Si se coloca una mezcla de gases en un recipiente con paredes porosas, los gases se derraman a través de las pequeñas aberturas en las paredes. Los gases más ligeros pasan por las pequeñas aberturas más rápidamente (a mayor velocidad) que los más pesados (Figura\(\PageIndex{2}\)). En 1832, Thomas Graham estudió las tasas de derrame de diferentes gases y formuló la ley de derrame de Graham: La tasa de derrame de un gas es inversamente proporcional a la raíz cuadrada de la masa de sus partículas:

\[\textrm{rate of effusion}∝\dfrac{1}{\sqrt{ℳ}} \nonumber \]

Esto significa que si dos gases A y B están a la misma temperatura y presión, la relación de sus tasas de efusión es inversamente proporcional a la relación de las raíces cuadradas de las masas de sus partículas:

\[\dfrac{\textrm{rate of effusion of B}}{\textrm{rate of effusion of A}}=\dfrac{\sqrt{ℳ_\ce{A}}}{\sqrt{ℳ_\ce{B}}} \nonumber \]

Figura\(\PageIndex{3}\): Un globo lleno de aire (el azul) permanece lleno durante la noche. Un globo lleno de helio (el verde) se desinfla parcialmente porque los átomos de helio más pequeños y ligeros se derraman a través de pequeños agujeros en el caucho mucho más fácilmente que las moléculas más pesadas de nitrógeno y oxígeno que se encuentran en el aire. (crédito: modificación de obra por Mark Ott)

Ejemplo\(\PageIndex{1}\): Applying Graham’s Law to Rates of Effusion

Calcular la relación entre la tasa de derrame de hidrógeno y la tasa de derrame de oxígeno.

Solución

De la ley de Graham, tenemos:

\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{\sqrt{1.43\cancel{g\: L^{−1}}}}{\sqrt{0.0899\cancel{g\: L^{−1}}}}=\dfrac{1.20}{0.300}=\dfrac{4}{1}} \nonumber \]

Uso de masas molares:

\[\dfrac{\textrm{rate of effusion of hydrogen}}{\textrm{rate of effusion of oxygen}}=\mathrm{\dfrac{32\cancel{g\: mol^{−1}}}{2\cancel{g\: mol^{−1}}}=\dfrac{\sqrt{16}}{\sqrt{1}}=\dfrac{4}{1}} \nonumber \]

El hidrógeno se funde cuatro veces más rápido que el oxígeno.

Ejercicio\(\PageIndex{1}\)

A una presión y temperatura particulares, el gas nitrógeno se funde a una velocidad de 79 ml/s. usando el mismo aparato a la misma temperatura y presión, ¿a qué velocidad se derramará el dióxido de azufre?

Contestar: 52 ML/s

Aquí hay otro ejemplo, haciendo el punto sobre cómo los tiempos determinantes difieren de determinar las tasas.

Ejemplo\(\PageIndex{2}\): Effusion Time Calculations

Se necesitan 243 s para que 4.46 × 10 ⁻⁵ mol Xe se derrame a través de un pequeño agujero. En las mismas condiciones, ¿cuánto tiempo tardará 4.46 × 10 ⁻⁵ mol Ne en derramarse?

Solución

Es importante resistir la tentación de usar los tiempos directamente, y recordar cómo la tasa se relaciona con el tiempo así como cómo se relaciona con la masa. Recordemos la definición de tasa de derrame:

\[\textrm{rate of effusion}=\dfrac{\textrm{amount of gas transferred}}{\textrm{time}}\nonumber \]

y combinarlo con la ley de Graham:

\[\dfrac{\textrm{rate of effusion of gas Xe}}{\textrm{rate of effusion of gas Ne}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]

Para obtener:

\[\dfrac{\dfrac{\textrm{amount of Xe transferred}}{\textrm{time for Xe}}}{\dfrac{\textrm{amount of Ne transferred}}{\textrm{time for Ne}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}\nonumber \]

Observando que cantidad de A = cantidad de B, y resolviendo por tiempo para Ne:

\[\dfrac{\dfrac{\cancel{\textrm{amount of Xe}}}{\textrm{time for Xe}}}{\dfrac{\cancel{\textrm{amount of Ne}}}{\textrm{time for Ne}}}=\dfrac{\textrm{time for Ne}}{\textrm{time for Xe}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}}=\dfrac{\sqrt{ℳ_\ce{Ne}}}{\sqrt{ℳ_\ce{Xe}}} \nonumber \]

y valores sustitutos:

\[\mathrm{\dfrac{time\: for\: Ne}{243\:s}=\sqrt{\dfrac{20.2\cancel{g\: mol}}{131.3\cancel{g\: mol}}}=0.392}\nonumber \]

Finalmente, resuelva para la cantidad deseada:

\[\mathrm{time\: for\: Ne=0.392×243\:s=95.3\:s}\nonumber \]

Tenga en cuenta que esta respuesta es razonable: Dado que Ne es más ligero que Xe, la tasa de derrame para Ne será mayor que la de\(\ce{Xe}\), lo que significa que el tiempo de efusión para Ne será menor que el de Xe.

Ejercicio\(\PageIndex{2}\)

Un globo de fiesta lleno de helio se\(\dfrac{2}{3}\) desinfla a su volumen original en 8.0 horas. ¿Cuánto tiempo tardará un globo idéntico lleno del mismo número de moles de aire (= 28.2 g/mol) en desinflarse a\(\dfrac{1}{2}\) su volumen original?

Contestar: 32 h

Finalmente, aquí hay un ejemplo más que muestra cómo calcular la masa molar a partir de los datos de la tasa de efusión.

Ejemplo\(\PageIndex{3}\): Determining Molar Mass Using Graham’s Law

Un gas desconocido emite 1.66 veces más rápidamente que el CO ₂. ¿Cuál es la masa molar del gas desconocido? ¿Se puede hacer una conjetura razonable en cuanto a su identidad?

Solución

De la ley de Graham, tenemos:

\[\mathrm{\dfrac{rate\: of\: effusion\: of\: Unknown}{rate\: of\: effusion\: of\: CO_2}}=\dfrac{\sqrt{ℳ_\mathrm{CO_2}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]

Conecte los datos conocidos:

\[\dfrac{1.66}{1}=\dfrac{\sqrt{44.0\:\ce{g/mol}}}{\sqrt{ℳ_{Unknown}}} \nonumber \]

Resolver:

\[ℳ_{Unknown}=\mathrm{\dfrac{44.0\:g/mol}{(1.66)^2}=16.0\:g/mol} \nonumber \]

El gas bien podría ser CH ₄, el único gas con esta masa molar.

Ejercicio

El gas hidrógeno fluye a través de un recipiente poroso 8.97 veces más rápido que un gas desconocido. Estimar la masa molar del gas desconocido.

Contestar: 163 g/mol

Aplicación: Uso de Difusión para Enriquecimiento de Uranio

La difusión gaseosa se ha utilizado para producir uranio enriquecido para su uso en centrales nucleares y armas. El uranio natural contiene solo 0.72% de ²³⁵ U, el tipo de uranio que es “fisible”, es decir, capaz de sostener una reacción en cadena de fisión nuclear. Los reactores nucleares requieren combustible que sea 2— 5% ²³⁵ U, y las bombas nucleares necesitan concentraciones aún más altas. Una forma de enriquecer el uranio a los niveles deseados es aprovechar la ley de Graham. En una planta de enriquecimiento por difusión gaseosa, el hexafluoruro de uranio (UF ₆, el único compuesto de uranio que es lo suficientemente volátil para funcionar) se bombea lentamente a través de grandes recipientes cilíndricos llamados difusores, los cuales contienen barreras porosas con aberturas microscópicas. El proceso es uno de difusión porque el otro lado de la barrera no es evacuado. Las moléculas ²³⁵ UF ₆ tienen una velocidad promedio mayor y se difunden a través de la barrera un poco más rápido que las moléculas ²³⁸ UF ₆ más pesadas. El gas que ha pasado a través de la barrera está ligeramente enriquecido en ²³⁵ UF ₆ y el gas residual está ligeramente agotado. La pequeña diferencia en pesos moleculares entre ²³⁵ UF ₆ y ²³⁸ UF ₆ solo aproximadamente 0.4% de enriquecimiento, se logra en un difusor (Figura\(\PageIndex{4}\)). Pero conectando muchos difusores en una secuencia de etapas (llamada cascada), se puede alcanzar el nivel deseado de enriquecimiento.

Figura\(\PageIndex{4}\): En un difusor, se bombea UF ₆ gaseoso a través de una barrera porosa, que separa parcialmente ²³⁵ UF ₆ de ²³⁸ UF ₆ El UF ₆ debe pasar a través de muchas unidades difusoras grandes para lograr un enriquecimiento suficiente en ²³⁵U.

La separación a gran escala de ²³⁵ UF ₆ gaseosos de ²³⁸ UF ₆ se realizó por primera vez durante la Segunda Guerra Mundial, en la instalación de energía atómica en Oak Ridge, Tennessee, como parte del Proyecto Manhattan (el desarrollo de la primera bomba atómica). Aunque la teoría es simple, esto requirió superar muchos desafíos técnicos desalentadores para que funcione en la práctica. La barrera debe tener orificios pequeños y uniformes (alrededor de 10 ^—6 cm de diámetro) y ser lo suficientemente porosa para producir altos caudales. Todos los materiales (la barrera, los tubos, los recubrimientos superficiales, los lubricantes y las juntas) deben poder contener, pero no reaccionar con, el UF ₆ altamente reactivo y corrosivo.

Debido a que las plantas de difusión gaseosa requieren cantidades muy grandes de energía (para comprimir el gas a las altas presiones requeridas y conducirlo a través de la cascada del difusor, para eliminar el calor producido durante la compresión, etc.), ahora está siendo reemplazado por tecnología de centrífuga de gas, que requiere mucha menos energía. Un tema político candente actual es cómo negarle esta tecnología a Irán, para evitar que produzca suficiente uranio enriquecido para que lo utilicen para fabricar armas nucleares.

Resumen

Los átomos gaseosos y las moléculas se mueven libre y aleatoriamente por el espacio. La difusión es el proceso mediante el cual los átomos gaseosos y las moléculas se transfieren de regiones de concentración relativamente alta a regiones de concentración relativamente baja. El derrame es un proceso similar en el que las especies gaseosas pasan de un recipiente a un vacío a través de orificios muy pequeños. Las tasas de derrame de gases son inversamente proporcionales a las raíces cuadradas de sus densidades o a las raíces cuadradas de las masas de sus átomos/moléculas (ley de Graham).

Ecuaciones Clave

\(\textrm{rate of diffusion}=\dfrac{\textrm{amount of gas passing through an area}}{\textrm{unit of time}}\)
\(\dfrac{\textrm{rate of effusion of gas A}}{\textrm{rate of effusion of gas B}}=\dfrac{\sqrt{m_B}}{\sqrt{m_A}}=\dfrac{\sqrt{ℳ_B}}{\sqrt{ℳ_A}}\)

Resumen

difusión: movimiento de un átomo o molécula de una región de concentración relativamente alta a una de concentración relativamente baja (discutido en este capítulo con respecto a especies gaseosas, pero aplicable a especies en cualquier fase)

derrame: transferencia de átomos gaseosos o moléculas de un recipiente a un vacío a través de aberturas muy pequeñas

Ley de derrame de Graham: las tasas de difusión y derrame de gases son inversamente proporcionales a las raíces cuadradas de sus masas moleculares

camino libre medio: distancia promedio que recorre una molécula entre colisiones

tasa de difusión: cantidad de gas que se difunde a través de un área determinada durante un tiempo determinado