9.E: Gases (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 75792

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

9.1: Presión de gas

Q9.1.1

¿Por qué los cuchillos afilados son más efectivos que los cuchillos opacos (Pista: piensa en la definición de presión)?

S9.1.1

El filo de un cuchillo que ha sido afilado tiene una superficie más pequeña que un cuchillo sin filo. Dado que la presión es fuerza por unidad de área, una cuchilla afilada ejercerá una mayor presión con la misma cantidad de fuerza y cortará el material de manera más efectiva.

Q9.1.2

¿Por qué algunos puentes pequeños tienen límites de peso que dependen de cuántas ruedas o ejes tenga el vehículo de cruce?

Q9.1.3

¿Por qué deberías rodar o arrastrarte por el estómago en lugar de caminar por un estanque poco congelado?

S9.1.3

Acostado distribuye tu peso sobre una superficie más grande, ejerciendo menos presión sobre el hielo en comparación con estar de pie. Si ejerce menos presión, es menos probable que rompa hielo delgado.

Q9.1.4

Una presión barométrica típica en Redding, California, es de aproximadamente 750 mm Hg. Calcula esta presión en atm y kPa.

Q9.1.5

Una presión barométrica típica en Denver, Colorado, es de 615 mm Hg. ¿Qué es esta presión en atmósferas y kilopascales?

S9.1.5

0.809 atm; 82.0 kPa

Q9.1.6

Una presión barométrica típica en Kansas City es de 740 torr. ¿Cuál es esta presión en atmósferas, en milímetros de mercurio, y en kilopascales?

Q9.1.7

Los medidores de presión de neumáticos canadienses están marcados en unidades de kilopascales. ¿Qué lectura en tal calibre corresponde a 32 psi?

S9.1.7

2.2 × 10 ² kPa

Q9.1.8

Durante los aterrizajes vikingos en Marte, se determinó que la presión atmosférica era en promedio de unos 6.50 milibares (1 bar = 0.987 atm). ¿Cuál es esa presión en torr y kPa?

Q9.1.9

La presión de la atmósfera sobre la superficie del planeta Venus es de aproximadamente 88.8 atm. Compare esa presión en psi con la presión normal en la tierra al nivel del mar en psi.

S9.1.9

Tierra: 14.7 lb en ^—2; Venus: 13.1× 10 ³ lb en ⁻²

Q9.1.10

Un catálogo de laboratorio médico describe la presión en un cilindro de un gas como 14.82 MPa. ¿Cuál es la presión de este gas en atmósferas y torr?

Q9.1.11

Considera este escenario y responde las siguientes preguntas: En un día a mediados de agosto en el noreste de Estados Unidos, apareció en el diario local la siguiente información: presión atmosférica a nivel del mar 29.97 pulg., 1013.9 mbar.

¿Cuál era la presión en kPa?
La presión cerca de la costa en el noreste de Estados Unidos generalmente se reporta cerca de 30.0 pulg. Hg. Durante un huracán, la presión puede caer cerca de 28.0 in. Hg. Calcular la caída de presión en torr.

S9.1.11

a) 101,5 kPa; b) caída de 51 torr

Q9.1.12

¿Por qué es necesario utilizar un líquido no volátil en un barómetro o manómetro?

Q9.1.13

La presión de una muestra de gas se mide al nivel del mar con un manómetro de extremo cerrado. El líquido en el manómetro es mercurio. Determinar la presión del gas en:

torr
Pa
bar

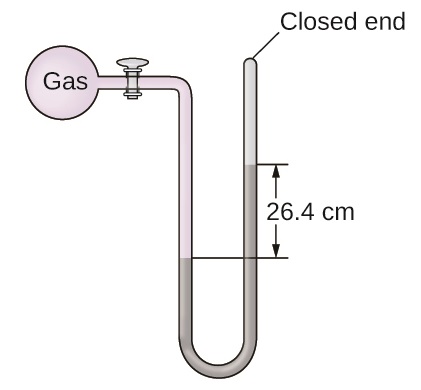
S9.1.13

a) 264 torr; b) 35.200 Pa; c) 0.352 bar

Q9.1.14

La presión de una muestra de gas se mide con un manómetro de extremo abierto, parcialmente mostrado a la derecha. El líquido en el manómetro es mercurio. Suponiendo que la presión atmosférica es de 29.92 pulg. Hg, determinar la presión del gas en:

torr
Pa
bar

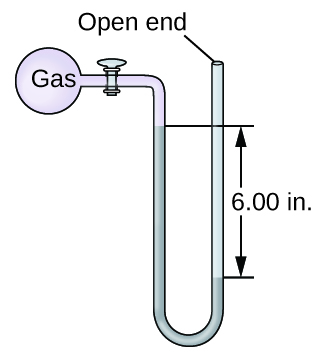
Q9.1.15

La presión de una muestra de gas se mide al nivel del mar con un manómetro de mercurio de extremo abierto. Suponiendo que la presión atmosférica es 760.0 mm Hg, determine la presión del gas en:

mm Hg
atm
kPa

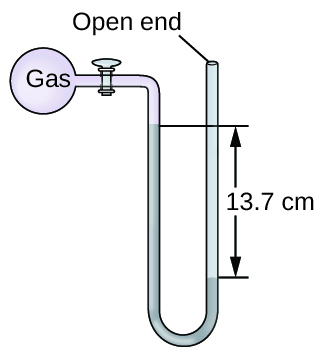
S9.1.15

a) 623 mm Hg; b) 0.820 atm; c) 83.1 kPa

Q9.1.16

La presión de una muestra de gas se mide al nivel del mar con un manómetro de mercurio de extremo abierto. Suponiendo que la presión atmosférica es 760 mm Hg, determine la presión del gas en:

mm Hg
atm
kPa

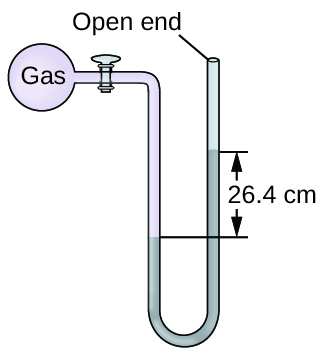
Q9.1.17

¿Cómo afectaría el uso de un líquido volátil a la medición de un gas usando manómetros abiertos vs. manómetros de extremo cerrado?

S9.1.17

Con un manómetro de extremo cerrado, no se observaría ningún cambio, ya que el líquido vaporizado aportaría presiones iguales y opuestas en ambos brazos del tubo del manómetro. Sin embargo, con un manómetro abierto, se obtendría una lectura de presión del gas mayor de lo esperado, ya que P _gas = P _atm + P _{vol líquido}.

9.2: Relación de Presión, Volumen, Cantidad y Temperatura: La Ley de Gas Ideal

Q9.2.1

En ocasiones, dejar una bicicleta al sol en un día caluroso provocará un reventón. ¿Por qué?

Q9.2.2

Explique cómo cambia el volumen de las burbujas agotadas por un buceador (Figura) a medida que suben a la superficie, asumiendo que permanecen intactas.

S9.2.2

A medida que suben las burbujas, la presión disminuye, por lo que su volumen aumenta como sugiere la ley de Boyle.

Q9.2.3

Una forma de afirmar la ley de Boyle es “Siendo todas las demás cosas iguales, la presión de un gas es inversamente proporcional a su volumen”. a) ¿Cuál es el significado del término “inversamente proporcional”? b) ¿Cuáles son las “otras cosas” que deben ser iguales?

Q9.2.4

Una forma alternativa de afirmar la ley de Avogadro es “Siendo todas las demás cosas iguales, el número de moléculas en un gas es directamente proporcional al volumen del gas”.

¿Cuál es el significado del término “directamente proporcional”?
¿Cuáles son las “otras cosas” que deben ser iguales?

S9.2.4

a) El número de partículas en el gas aumenta a medida que aumenta el volumen. (b) temperatura, presión

Q9.2.5

¿Cómo cambiaría la gráfica de la Figura si se duplicara el número de moles de gas en la muestra utilizada para determinar la curva?

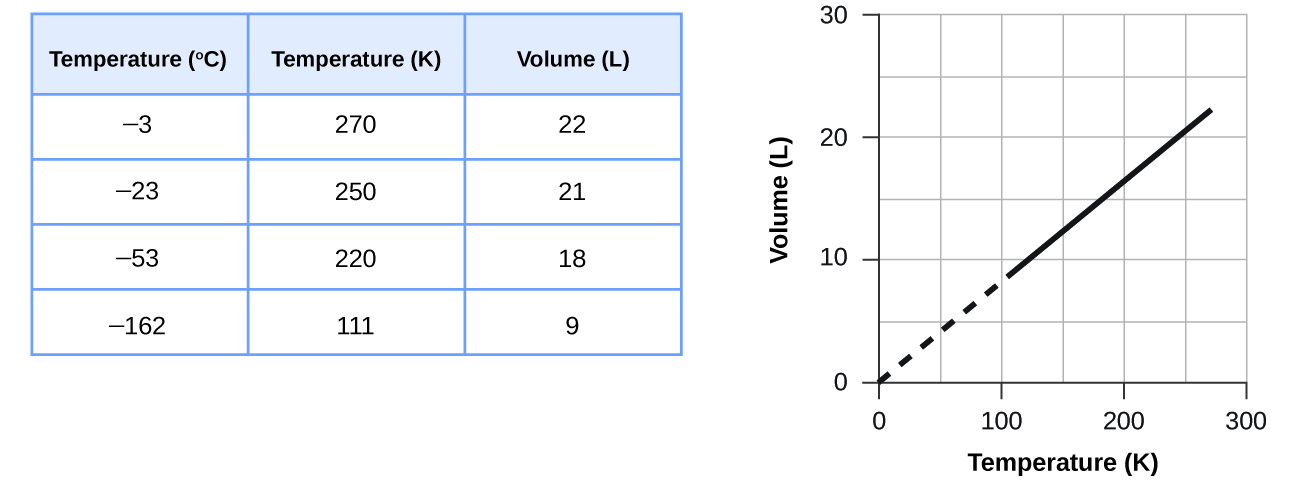
El volumen y la temperatura se relacionan linealmente para 1 mol de gas metano a una presión constante de 1 atm. Si la temperatura está en kelvin, el volumen y la temperatura son directamente proporcionales. La línea se detiene a 111 K porque el metano se licua a esta temperatura; cuando se extrapola, cruza el origen de la gráfica, lo que representa una temperatura de cero absoluto.

Q9.2.6

¿Cómo cambiaría la gráfica de la Figura si se duplicara el número de moles de gas en la muestra utilizada para determinar la curva?

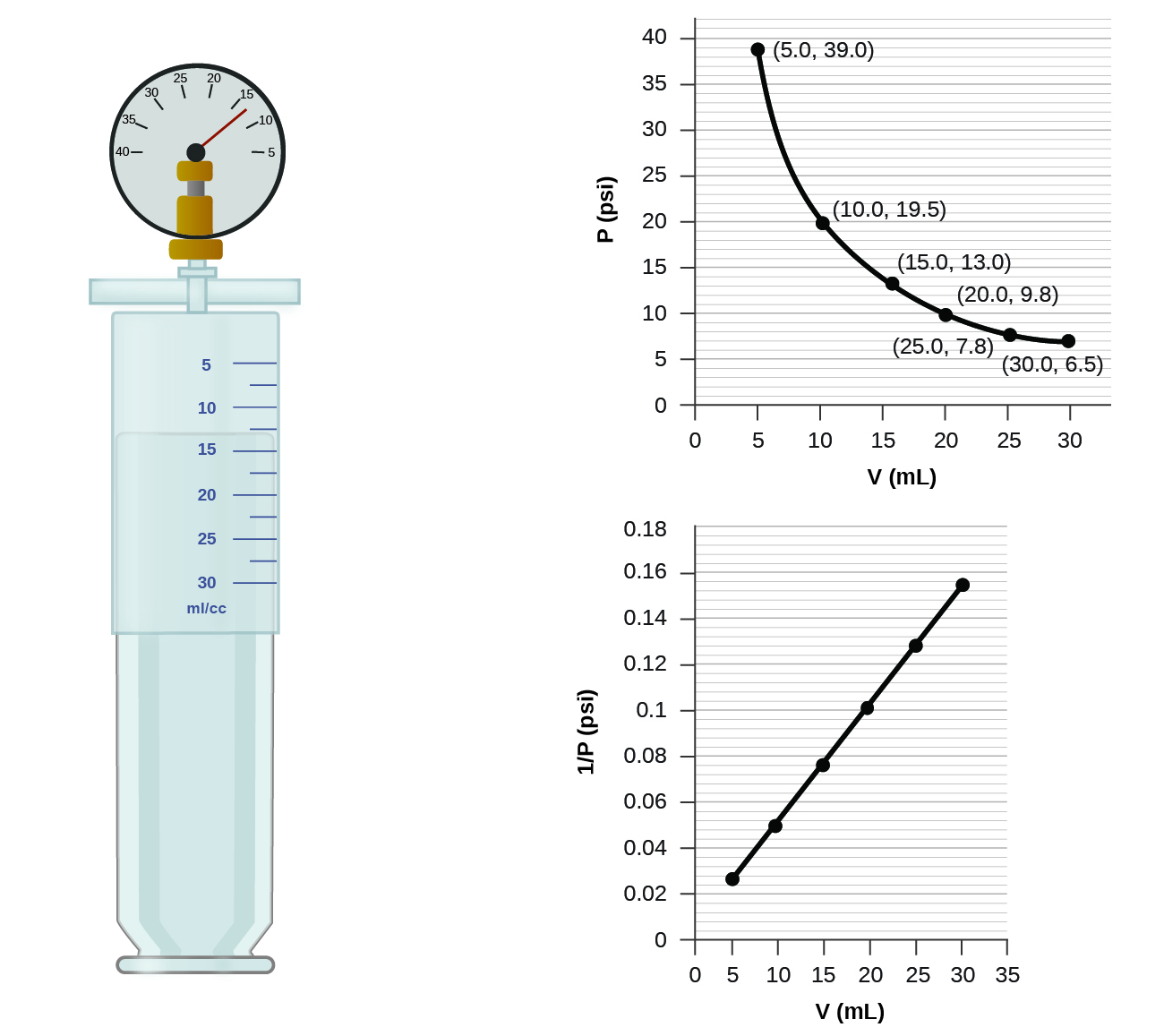
Cuando un gas ocupa un volumen menor, ejerce una presión mayor; cuando ocupa un volumen mayor, ejerce una presión menor (asumiendo que la cantidad de gas y la temperatura no cambian). Dado que P y V son inversamente proporcionales, una gráfica de\(1/P\) vs.\(V\) es lineal.

S9.2.6

La curva estaría más a la derecha y más arriba arriba, pero la misma forma básica.

Q9.2.7

Además de los datos que se encuentran en la Figura, ¿qué otra información necesitamos para encontrar la masa de la muestra de aire utilizada para determinar la gráfica?

Q9.2.8

Determinar el volumen de 1 mol de gas CH ₄ a 150 K y 1 atm, utilizando la Figura.

S9.2.8

16.3 a 16.5 L

Q9.2.9

Determinar la presión del gas en la jeringa que se muestra en la Figura cuando su volumen es de 12.5 mL, utilizando:

la gráfica apropiada
Ley de Boyle

Q9.2.10

Se usa una lata de pulverización hasta que esté vacía excepto el gas propulsor, que tiene una presión de 1344 torr a 23 °C. Si la lata se lanza al fuego (T = 475 °C), ¿cuál será la presión en la lata caliente?

S9.2.10

3.40 × 10 ³ torr

Q9.2.11

¿Cuál es la temperatura de una muestra de 11.2-L de monóxido de carbono, CO, a 744 torr si ocupa 13.3 L a 55 °C y 744 torr?

S9.2.11

debemos usar\(\dfrac{P_1V_1}{T_1} =\dfrac{P_2V_2}{T_2}\) y resolver para\(T_1\)

\(T_1 = \dfrac{P_1V_1T_2}{P_2V_2}\)

Donde:

\(P_1 = 744\: torr\)

\(V_1 = 11.2\: L\)

\(P_2 = 744\: torr\)

\(V_2 = 13.3\: L\)

\(T_2 = 328.15°\: K\)

\(\dfrac{(744\: torr)(11.2\: L)(328.15°\: K)}{(744\: torr)(13.3\: L)} = 276°\: K\)

276°K; 3°C

Q9.2.12

Un volumen de 2.50-L de hidrógeno medido a —196 °C se calienta a 100 °C. Calcular el volumen del gas a la temperatura más alta, suponiendo que no haya cambios en la presión.

S9.2.13

12.1 L

Q9.2.14

Un globo inflado con tres respiraciones de aire tiene un volumen de 1.7 L. A la misma temperatura y presión, ¿cuál es el volumen del globo si se agregan cinco respiraciones más del mismo tamaño al globo?

Q9.2.15

Un globo meteorológico contiene 8.80 moles de helio a una presión de 0.992 atm y una temperatura de 25 °C a nivel del suelo. ¿Cuál es el volumen del globo bajo estas condiciones?

S9.2.15

217 L

Q9.2.16

El volumen de una bolsa de aire de automóvil fue de 66.8 L cuando se infló a 25 °C con 77.8 g de gas nitrógeno. ¿Cuál era la presión en la bolsa en kPa?

Q9.2.17

¿Cuántos moles de trifluoruro de boro gaseoso, BF ₃, están contenidos en una bombilla de 4.3410-L a 788.0 K si la presión es de 1.220 atm? ¿Cuántos gramos de BF ₃?

S9.2.17

8.190 × 10 ^—2 mol; 5.553 g

Q9.2.18

El yodo, I ₂, es un sólido a temperatura ambiente pero sublima (se convierte de un sólido en un gas) cuando se calienta. ¿Cuál es la temperatura en una bombilla de 73.3-mL que contiene 0.292 g de vapor I ₂ a una presión de 0.462 atm?

S9.2.18

1.) Usa la ecuación\(PV =nRT\) and solve for \(T\)

\(T= \dfrac{PV}{nR}\)

2.) convert grams of I₂ to moles of I₂ and convert mL to L

\(0.292g\: \ce{I2}\times \dfrac{1\: mole\: \ce{I2}}{253.8g\: \ce{I2}} = 1.15 \times10^{-3}\: moles\: \ce{I2}\)

\(73.3\:mL = 0.0733\:L\)

3.) Use these values along with \(R= 0.08206\: \dfrac{atm\:L}{mole\:°K}\) to solve for \(T\)

\(T= \dfrac{(0.462\: \cancel{atm})(0.0733\:\cancel{L})}{(1.15\times10^{-3}\: \cancel{moles})(0.08206\: \dfrac{\cancel{atm}\:\cancel{L}}{\cancel{mole}\:°K})} = 359\: °K \)

359°K ; 86°C

Q9.2.19

How many grams of gas are present in each of the following cases?

0.100 L of CO₂ at 307 torr and 26 °C
8.75 L of C₂H₄, at 378.3 kPa and 483 K
221 mL of Ar at 0.23 torr and –54 °C

S9.2.19

(a) 7.24 × 10^–2 g; (b) 23.1 g; (c) 1.5 × 10^–4 g

Q9.2.20

A high altitude balloon is filled with 1.41 × 10⁴ L of hydrogen at a temperature of 21 °C and a pressure of 745 torr. What is the volume of the balloon at a height of 20 km, where the temperature is –48 °C and the pressure is 63.1 torr?

Q9.2.21

A cylinder of medical oxygen has a volume of 35.4 L, and contains O₂ at a pressure of 151 atm and a temperature of 25 °C. What volume of O₂ does this correspond to at normal body conditions, that is, 1 atm and 37 °C?

S9.2.21

5561 L

Q9.2.22

A large scuba tank (Figure) with a volume of 18 L is rated for a pressure of 220 bar. The tank is filled at 20 °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?

Q9.2.23

A 20.0-L cylinder containing 11.34 kg of butane, C₄H₁₀, was opened to the atmosphere. Calculate the mass of the gas remaining in the cylinder if it were opened and the gas escaped until the pressure in the cylinder was equal to the atmospheric pressure, 0.983 atm, and a temperature of 27 °C.

S9.2.23

46.4 g

Q9.2.24

While resting, the average 70-kg human male consumes 14 L of pure O₂ per hour at 25 °C and 100 kPa. How many moles of O₂ are consumed by a 70 kg man while resting for 1.0 h?

Q9.2.25

For a given amount of gas showing ideal behavior, draw labeled graphs of:

the variation of P with V
the variation of V with T
the variation of P with T
the variation of \(\dfrac{1}{P}\) with V

Q9.2.26

For a gas exhibiting ideal behavior:

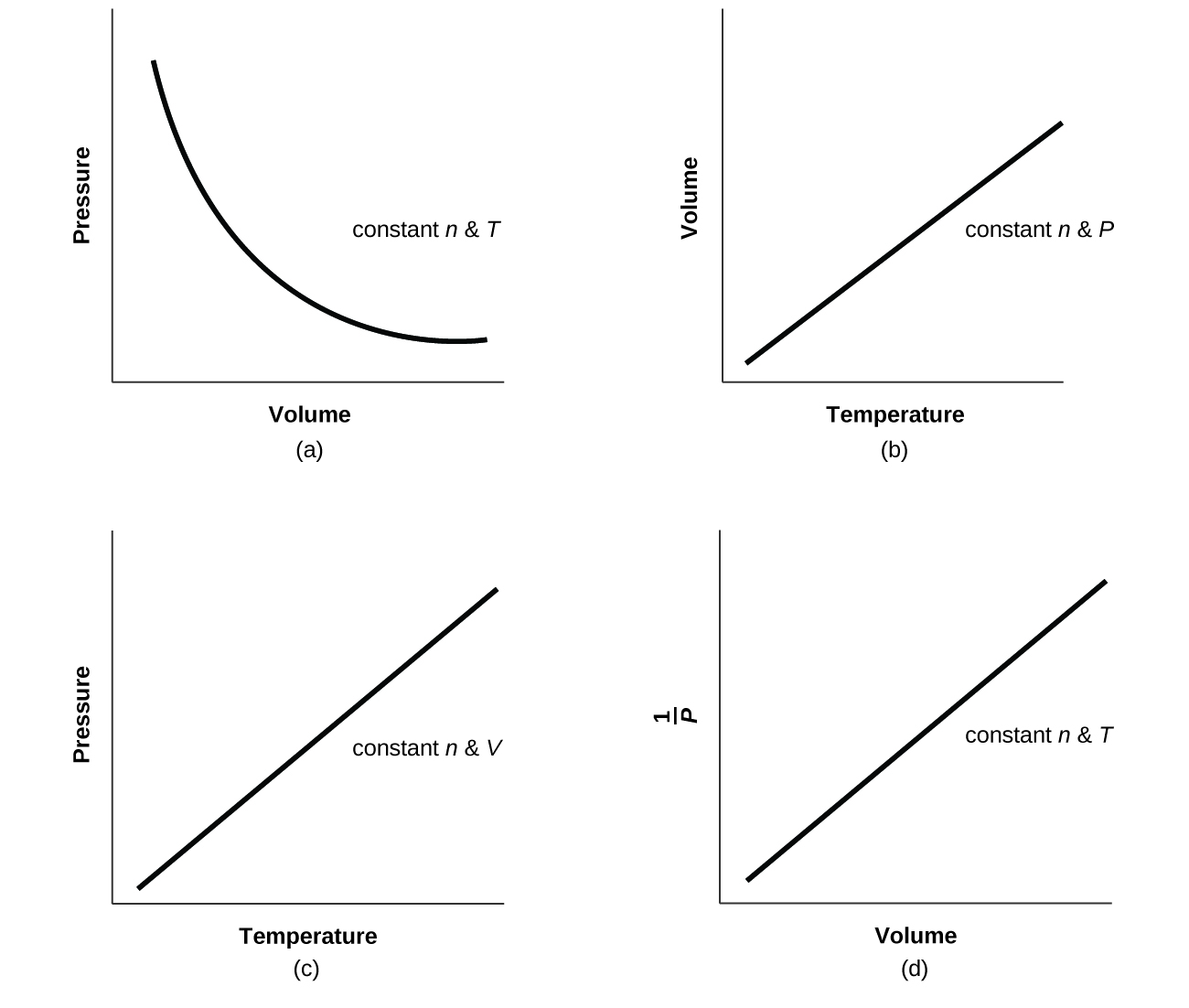
Q9.2.27

Un litro de gas metano, CH ₄, en STP contiene más átomos de hidrógeno que un litro de gas hidrógeno puro, H ₂, en STP. Usando la ley de Avogadro como punto de partida, explique por qué.

Q9.2.28

El efecto de los clorofluorocarbonos (como CCl ₂ F ₂) sobre el agotamiento de la capa de ozono es bien conocido. El uso de sustitutos, como CH ₃ CH ₂ F (g), para los clorofluorocarbonos, ha corregido en gran medida el problema. Calcular el volumen ocupado por 10.0 g de cada uno de estos compuestos en STP:

CCl ₂ F ₂ (g)
CH ₃ CH ₂ F (g)

S9.2.28

a) 1.85 L CCl ₂ F ₂; b) 4.66 L CH ₃ CH ₂ F

Q9.2.29

A medida que 1 g del radio del elemento radiactivo se descompone a lo largo de 1 año, produce 1.16 × 10 ¹⁸ partículas alfa (núcleos de helio). Cada partícula alfa se convierte en un átomo de gas helio. ¿Cuál es la presión en pascal del gas helio producido si ocupa un volumen de 125 mL a una temperatura de 25 °C?

Q9.2.30

Se libera un globo que mide 100.21 L a 21 °C y 0.981 atm y apenas despeja la cima del Monte Crumpet en Columbia Británica. Si el volumen final del balón es de 144.53 L a una temperatura de 5.24 °C, ¿cuál es la presión que experimenta el globo al despejar el Monte Crumpet?

S9.2.30

0.644 atm

Q9.2.31

Si la temperatura de una cantidad fija de un gas se duplica a volumen constante, ¿qué pasa con la presión?

Q9.2.32

Si el volumen de una cantidad fija de un gas se triplica a temperatura constante, ¿qué sucede con la presión?

S9.2.32

La presión disminuye en un factor de 3.

9.3: Estequiometría de Sustancias Gaseosas, Mezclas y Reacciones

Q9.3.1

¿Cuál es la densidad del gas de la risa, monóxido de dinitrógeno, N ₂ O, a una temperatura de 325 K y una presión de 113.0 kPa?

S9.3.1

1.) Primero convierta kPa a atm

\(113.0\:kPa\times\dfrac{1\:atm}{101.325\:kPa}=1.115\:atm\)

2.) El uso de la ecuación\(d=\dfrac{PM}{RT}\) donde d = densidad en g L ^-1 y M = masa molar en g mol ^-1

\(d=\dfrac{(1.115\:atm)(44.02\dfrac{g}{\cancel{mol}})}{(0.08206\: \dfrac{\cancel{atm}\:L}{\cancel{mole}\:\cancel{°K}})(325\:\cancel{°K})}=1.84\:\dfrac{g}{L}\)

Q9.3.2

Calcular la densidad de Freón 12, CF ₂ Cl ₂, a 30.0 °C y 0.954 atm.

S9.3.2

4.64 g L ⁻¹

Q9.3.3

¿Cuál es más denso a la misma temperatura y presión, aire seco o aire saturado de vapor de agua? Explique.

Q9.3.4

Un cilindro de O ₂ (g) utilizado en la respiración por pacientes con enfisema tiene un volumen de 3.00 L a una presión de 10.0 atm. Si la temperatura del cilindro es de 28.0 °C, ¿qué masa de oxígeno hay en el cilindro?

S9.3.4

38.8 g

Q9.3.5

¿Cuál es la masa molar de un gas si 0.0494 g del gas ocupa un volumen de 0.100 L a una temperatura 26 °C y una presión de 307 torr?

S9.3.5

1.) convertir torr a atm y °C a °K

\(307\:torr=0.404atm\)

\(26°C= 300.°K\)

2.) Usa la ecuación\(PV=nRT\) y resuelve para\(n\)

\(n=\dfrac{PV}{RT}\)

\(n=\dfrac{(0.404\:\cancel{atm})(0.100\:\cancel{L})}{(0.08206\dfrac{\cancel{atm}\:\cancel{L}}{mol\:\cancel{°K}})(300.\cancel{°K})}=0.00165\:moles\)

3.) Luego divida gramos por el número de moles para obtener la masa molar:

\(\dfrac{0.0494g}{0.00165\:moles}=30.0\dfrac{g}{mole}\)

Q9.3.6

¿Cuál es la masa molar de un gas si 0.281 g del gas ocupa un volumen de 125 mL a una temperatura de 126 °C y una presión de 777 torr?

S9.3.6

72.0 g mol ⁻¹

Q9.3.7

¿Cómo podría demostrar experimentalmente que la fórmula molecular del propeno es C ₃ H ₆, no CH ₂?

Q9.3.8

La densidad de cierto fluoruro gaseoso de fósforo es de 3.93 g/L a STP. Calcular la masa molar de este fluoruro y determinar su fórmula molecular.

S9.3.8

88.1 g mol ⁻¹; PF ₃

Q9.3.9

Considera esta pregunta: ¿Cuál es la fórmula molecular de un compuesto que contiene 39% C, 45% N y 16% H si 0.157 g del compuesto ocupa 125 mL con una presión de 99.5 kPa a 22 °C?

Esbozar los pasos necesarios para responder a la pregunta.
Contesta la pregunta.

Q9.3.10

Un cilindro de 36.0—L de un gas utilizado para la calibración de analizadores de gases sanguíneos en laboratorios médicos contiene 350 g de CO ₂, 805 g O ₂ y 4,880 g N ₂. A 25 grados C, ¿cuál es la presión en el cilindro en atmósferas?

S9.3.10

141 atm

Q9.3.11

Un cilindro de una mezcla de gases utilizada para la calibración de analizadores de gases sanguíneos en laboratorios médicos contiene 5.0% CO ₂, 12.0% O ₂, y el resto N ₂ a una presión total de 146 atm. ¿Cuál es la presión parcial de cada componente de este gas? (Los porcentajes dados indican el porcentaje de la presión total que se debe a cada componente.)

Q9.3.12

Una muestra de gas aislado del petróleo sin refinar contiene 90.0% CH ₄, 8.9% C ₂ H ₆ y 1.1% C ₃ H ₈ a una presión total de 307.2 kPa. ¿Cuál es la presión parcial de cada componente de este gas? (Los porcentajes dados indican el porcentaje de la presión total que se debe a cada componente.)

S9.3.12

CH ₄: 276 kPa; C ₂ H ₆: 27 kPa; C ₃ H ₈: 3.4 kPa

Q9.3.13

Una mezcla de 0.200 g de H ₂, 1.00 g de N ₂ y 0.820 g de Ar se almacena en un recipiente cerrado en STP. Encuentra el volumen del contenedor, asumiendo que los gases presentan un comportamiento ideal.

Q9.3.14

La mayoría de las mezclas de gas hidrógeno con gas oxígeno son explosivas. Sin embargo, una mezcla que contiene menos de 3.0% O ₂ no lo es. Si se agrega suficiente O ₂ a un cilindro de H ₂ a 33.2 atm para llevar la presión total a 34.5 atm, ¿la mezcla es explosiva?

S9.3.14

Sí

Q9.3.15

Un analizador de vapor de mercurio comercial puede detectar, en el aire, concentraciones de átomos de Hg gaseosos (que son venenosos) tan bajas como 2 × 10 ⁻⁶ mg/L de aire. A esta concentración, ¿cuál es la presión parcial del mercurio gaseoso si la presión atmosférica es de 733 torr a 26 °C?

Q9.3.16

Se colectó una muestra de monóxido de carbono sobre agua a una presión total de 756 torr y una temperatura de 18 °C. ¿Cuál es la presión del monóxido de carbono? (Ver Tabla para la presión de vapor del agua.)

S9.3.16

740 torr

Q9.3.17

En un experimento en un laboratorio de química general, un estudiante recolectó una muestra de un gas sobre agua. El volumen del gas fue de 265 mL a una presión de 753 torr y una temperatura de 27 °C. La masa del gas fue de 0.472 g. ¿Cuál fue la masa molar del gas?

Q9.3.18

Joseph Priestley primero preparó oxígeno puro calentando óxido mercúrico, HgO:

\(\ce{2HgO}(s)⟶\ce{2Hg}(l)+\ce{O2}(g)\)

Esbozar los pasos necesarios para responder a la siguiente pregunta: ¿Qué volumen de O ₂ a 23 °C y 0.975 atm se produce por la descomposición de 5.36 g de HGo?
Contesta la pregunta.

S9.3.18

a) Determinar los moles de HgO que se descomponen; mediante la ecuación química, determinar los moles de O ₂ producidos por la descomposición de esta cantidad de HgO; y determinar el volumen de O ₂ a partir de los moles de O ₂, temperatura y presión. b) 0.308 L

Q9.3.19

Cavendish preparó hidrógeno en 1766 mediante el novedoso método de pasar vapor a través de un cañón de pistola al rojo vivo:

\[\ce{4H2O}(g)+\ce{3Fe}(s)⟶\ce{Fe3O4}(s)+\ce{4H2}(g)\]

Esbozar los pasos necesarios para responder a la siguiente pregunta: ¿Qué volumen de H ₂ a una presión de 745 torr y una temperatura de 20 °C se puede preparar a partir de la reacción de 15.O g de H ₂ O?
Contesta la pregunta.

Q9.3.20

El clorofluorocarbono CCl ₂ F ₂ puede reciclarse en un compuesto diferente por reacción con hidrógeno para producir CH ₂ F ₂ (g), un compuesto útil en la fabricación química:

\[\ce{CCl2F2}(g)+\ce{4H2}(g)⟶\ce{CH2F2}(g)+\ce{2HCl}(g)\]

Esbozar los pasos necesarios para responder a la siguiente pregunta: ¿Qué volumen de hidrógeno a 225 atm y 35.5 °C se requeriría para reaccionar con 1 tonelada (1.000 × 10 ³ kg) de CCl ₂ F ₂?
Contesta la pregunta.

S9.3.20

Determinar la masa molar de CCl ₂ F ₂. A partir de la ecuación equilibrada, calcular los moles de H ₂ necesarios para la reacción completa. De la ley de gas ideal, convertir moles de H ₂ en volumen.
3.72 × 10 ³ L

Q9.3.21

Las bolsas de aire para automóviles se inflan con gas nitrógeno, el cual se forma por la descomposición de la azida sódica sólida (NaN ₃). El otro producto es sodio metálico. Calcular el volumen de gas nitrógeno a 27 °C y 756 torr formado por la descomposición de 125 g de azida sódica.

Q9.3.22

La cal, CaO, se produce calentando carbonato de calcio, CaCo ₃; el otro producto es el dióxido de carbono.

Esbozar los pasos necesarios para responder a la siguiente pregunta: ¿Qué volumen de dióxido de carbono a 875° y 0.966 atm se produce por la descomposición de 1 tonelada (1.000 × 10 ³ kg) de carbonato de calcio?
Contesta la pregunta.

S9.3.22

(a) Equilibrar la ecuación. Determinar los gramos de CO ₂ producidos y el número de moles. A partir de la ley de gas ideal, determinar el volumen de gas. b) 7.43 × 10 ⁵ L

Q9.3.23

Antes de que estuvieran disponibles baterías pequeñas, se usaban lámparas de carburo para las luces de bicicleta. El gas acetileno, C ₂ H ₂, y el hidróxido de calcio sólido se formaron por reacción de carburo de calcio, CaC ₂, con agua. El encendido del gas acetileno proporcionó la luz. Actualmente, las mismas lámparas son utilizadas por algunos espeleros, y el carburo de calcio se utiliza para producir acetileno para cañones de carburo.

Esbozar los pasos necesarios para responder a la siguiente pregunta: ¿Qué volumen de C ₂ _{H 2} a 1.005 atm y 12.2 °C se forma por la reacción de 15.48 g de CaC ₂ con agua?
Contesta la pregunta.

Q9.3.24

Calcular el volumen de oxígeno requerido para quemar 12.00 L de gas etano, C ₂ H ₆, para producir dióxido de carbono y agua, si los volúmenes de C ₂ H ₆ y O ₂ se miden en las mismas condiciones de temperatura y presión.

S9.3.24

42.00 L

Q9.3.25

¿Qué volumen de O ₂ en STP se requiere para oxidar 8.0 L de NO a STP a NO ₂? ¿Qué volumen de NO ₂ se produce en STP?

Q9.3.26

Considera las siguientes preguntas:

¿Cuál es el volumen total del CO ₂ (g) y H ₂ O (g) a 600 °C y 0.888 atm producido por la combustión de 1.00 L de C ₂ H ₆ (g) medido a STP?
¿Cuál es la presión parcial de H ₂ O en los gases producto?

S9.3.26

(a) 18.0 L; (b) 0.533 atm

Q9.3.27

El metanol, CH ₃ OH, se produce industrialmente mediante la siguiente reacción:

\[\ce{CO}(g)+\ce{2H2}(g)\xrightarrow{\textrm{ copper catalyst 300 °C, 300 atm }}\ce{CH3OH}(g)\]

Q9.3.28

Suponiendo que los gases se comportan como gases ideales, encuentre la relación entre el volumen total de los reactivos y el volumen final.

Q9.3.29

¿Qué volumen de oxígeno a 423.0 K y una presión de 127.4 kPa se produce por la descomposición de 129.7 g de BaO ₂ a BaO y O ₂?

S9.3.29

10.57 L O ₂

Q9.3.30

Una muestra de 2.50-L de un gas incoloro en STP se descompuso para dar 2.50 L de N ₂ y 1.25 L de O ₂ en STP. ¿Qué es el gas incoloro?

Q9.3.31

El etanol, C _2H ₅ OH, se produce industrialmente a partir de etileno, C _2H ₄, mediante la siguiente secuencia de reacciones:

\[\ce{3C2H4 + 2H2SO4⟶C2H5HSO4 + (C2H5)2SO4}\]

\[\ce{C2H5HSO4 + (C2H5)2SO4 + 3H2O⟶3C2H5OH + 2H2SO4}\]

¿Qué volumen de etileno a STP se requiere para producir 1.000 toneladas métricas (1000 kg) de etanol si el rendimiento general de etanol es 90.1%?

S9.3.31

5.40 × 10 ⁵ L

Q9.3.32

Una molécula de hemoglobina se combinará con cuatro moléculas de oxígeno. Si 1.0 g de hemoglobina se combina con 1.53 mL de oxígeno a temperatura corporal (37 °C) y una presión de 743 torr, ¿cuál es la masa molar de la hemoglobina?

Q9.3.33

Una muestra de un compuesto de xenón y flúor se confinó en un bulbo con una presión de 18 torr. Se añadió hidrógeno al bulbo hasta que la presión fue de 72 torr. El paso de una chispa eléctrica a través de la mezcla produjo Xe y HF. Después de eliminar el HF por reacción con KOH sólido, la presión final de xenón e hidrógeno sin reaccionar en el bulbo fue de 36 torr. ¿Cuál es la fórmula empírica del fluoruro de xenón en la muestra original? (Nota: Los fluoruros de xenón contienen solo un átomo de xenón por molécula.)

S9.3.33

XeF ₂

Q9.3.34

Un método de análisis de aminoácidos es el método van Slyke. Los grupos amino característicos (-NH ₂) en el material proteico se dejan reaccionar con ácido nitroso, HNO ₂, para formar N ₂ gas. A partir del volumen del gas, se puede determinar la cantidad de aminoácido. Una muestra de 0.0604-g de una muestra biológica que contenía glicina, CH ₂ (NH ₂) COOH, se analizó por el método de van Slyke y arrojó 3.70 mL de N ₂ colectados sobre agua a una presión de 735 torr y 29 °C. ¿Cuál fue el porcentaje de glicina en la muestra?

\(\ce{CH2(NH2)CO2H + HNO2⟶CH2(OH)CO2H + H2O + N2}\)

9.4: Derrame y Difusión de Gases

Q9.4.1

Se encuentra que un globo lleno de gas helio tarda 6 horas en desinflarse al 50% de su volumen original. ¿Cuánto tiempo tardará en que un globo idéntico lleno del mismo volumen de gas hidrógeno (en lugar de helio) disminuya su volumen en un 50%?

S9.4.1

4.2 horas

Q9.4.2

Explique por qué los números de moléculas no son idénticos en las bombillas izquierda y derecha mostradas en la ilustración central de la Figura.

Q9.4.3

A partir de la definición de tasa de derrame y el hallazgo de Graham que relaciona la tasa y la masa molar, muestran cómo derivar la ecuación de la ley de Graham, relacionando las tasas relativas de derrame de dos gases con sus masas moleculares.

S9.4.3

El derrame se puede definir como el proceso por el cual un gas escapa a través de un agujero de alfiler hacia un vacío. La ley de Graham establece que con una mezcla de dos gases A y B:\(\mathrm{\left(\dfrac{rate\: A}{rate\: B}\right)=\left(\dfrac{molar\: mass\: of\: B}{molar\: mass\: of\: A}\right)^{1/2}}\). Tanto A como B están en el mismo contenedor a la misma temperatura, y por lo tanto tendrán la misma energía cinética:

\(\mathrm{KE_A=KE_BKE}=\dfrac{1}{2}mv^2\) Por lo tanto,\(\dfrac{1}{2}m_\ce{A}v^2_\ce{A}=\dfrac{1}{2}m_\ce{B}v^2_\ce{B}\) \(\dfrac{v^2_\ce{A}}{v^2_\ce{B}}=\dfrac{m_\ce{B}}{m_\ce{A}}\) \(\left(\dfrac{v^2_\ce{A}}{v^2_\ce{B}}\right)^{1/2}=\left(\dfrac{m_\ce{B}}{m_\ce{A}}\right)^{1/2}\) \(\dfrac{v_\ce{A}}{v_\ce{B}}=\left(\dfrac{m_\ce{B}}{m_\ce{A}}\right)^{1/2}\)

Q9.4.4

El agua pesada, D ₂ O (masa molar = 20.03 g mol ^—1), puede separarse del agua ordinaria, H ₂ O (masa molar = 18.01), como resultado de la diferencia en las velocidades relativas de difusión de las moléculas en la fase gaseosa. Calcular las tasas relativas de difusión de H ₂ O y D ₂ O.

Q9.4.5

¿Cuál de los siguientes gases se difunde más lentamente que el oxígeno? F ₂, Ne, N ₂ O, C ₂ H ₂, NO, Cl ₂, H ₂ S

S9.4.5

F ₂, N ₂ O, Cl ₂, H ₂ S

Q9.4.6

Durante la discusión de la difusión gaseosa para enriquecer uranio, se afirmó que ²³⁵ UF ₆ difunden 0.4% más rápido que ²³⁸ UF ₆. Mostrar el cálculo que soporta este valor. La masa molar de ²³⁵ UF ₆ = 235.043930 + 6 × 18.998403 = 349.034348 g/mol, y la masa molar de ²³⁸ UF ₆ = 238.050788 + 6 × 18.998403 = 352.041206 g/mol.

Q9.4.7

Calcular la tasa relativa de difusión de ¹ H ₂ (masa molar 2.0 g/mol) en comparación con la de ² H ₂ (masa molar 4.0 g/mol) y la tasa relativa de difusión de O ₂ (masa molar 32 g/mol) en comparación con la de O ₃ (masa molar 48 g/mol).

S9.4.7

1.4; 1.2

Q9.4.8

Un gas de identidad desconocida se difunde a una velocidad de 83.3 ml/s en un aparato de difusión en el que el dióxido de carbono se difunde a una velocidad de 102 ml/s. Calcular la masa molecular del gas desconocido.

Q9.4.9

Cuando dos tapones de algodón, uno humedecido con amoníaco y el otro con ácido clorhídrico, se insertan simultáneamente en extremos opuestos de un tubo de vidrio de 87.0 cm de largo, se forma un anillo blanco de NH ₄ Cl donde primero entran en contacto NH ₃ gaseoso y HCl gaseoso. (Pista: Calcule las tasas de difusión tanto para NH ₃ como para HCl, y averigüe cuánto más rápido se difunde NH ₃ que HCl).

\[\ce{NH3}(g)+\ce{HCl}(g)⟶\ce{NH4Cl}(s)\]

Q9.4.10

¿A aproximadamente qué distancia del tapón humedecido con amoníaco ocurre esto?

S9.4.10

51.7 cm

9.5: La teoría cinético-molecular

Q9.5.1

Utilizando los postulados de la teoría molecular cinética, explicar por qué un gas llena uniformemente un recipiente de cualquier forma.

Q9.5.2

¿Puede duplicarse la velocidad de una molécula dada en un gas a temperatura constante? Explica tu respuesta.

S9.5.2

Sí. En cualquier momento dado, hay un rango de valores de velocidades moleculares en una muestra de gas. Cualquier molécula puede acelerar o disminuir la velocidad ya que colisiona con otras moléculas. La velocidad promedio de todas las moléculas es constante a temperatura constante.

Q9.5.3

Describa lo que sucede con la energía cinética promedio de las moléculas de gas ideales cuando se cambian las condiciones de la siguiente manera:

La presión del gas se incrementa al reducir el volumen a temperatura constante.
La presión del gas se incrementa al aumentar la temperatura a volumen constante.
La velocidad promedio de las moléculas se incrementa en un factor de 2.

Q9.5.4

La distribución de las velocidades moleculares en una muestra de helio se muestra en la Figura. Si la muestra se enfría, ¿la distribución de velocidades se parecerá más a la de H ₂ o de H ₂ O? Explica tu respuesta.

S9.5.4

H ₂ O. El enfriamiento ralentiza las velocidades de los átomos de He, haciendo que se comporten como si fueran más pesados.

Q9.5.5

¿Cuál es la relación entre la energía cinética promedio de una molécula SO ₂ y la de una molécula de O ₂ en una mezcla de dos gases? ¿Cuál es la relación de las velocidades cuadráticas medias de raíz, u _rms, de los dos gases?

Q9.5.6

Una muestra de 1 L de CO inicialmente a STP se calienta a 546 °C, y su volumen se incrementa a 2 L.

¿Qué efecto tienen estos cambios en el número de colisiones de las moléculas del gas por unidad de área de la pared del contenedor?
¿Cuál es el efecto sobre la energía cinética promedio de las moléculas?
¿Cuál es el efecto en la velocidad cuadrática media de las moléculas?

S9.5.6

a) El número de colisiones por unidad de área de la pared del contenedor es constante. b) La energía cinética promedio se duplica. (c) La velocidad media cuadrática de la raíz aumenta a\(\sqrt{2}\) veces su valor inicial; u _rms es proporcional a\(\mathrm{KE_{avg}}\).

Q9.5.7

La velocidad media cuadrática de las moléculas H ₂ a 25 °C es de aproximadamente 1.6 km/s. ¿Cuál es la velocidad cuadrática media de una molécula de N ₂ a 25 °C?

Q9.5.8

Responde las siguientes preguntas:

¿La presión del gas en el globo aerostático que se muestra en la apertura de este capítulo es mayor, menor o igual a la de la atmósfera exterior del globo?
¿La densidad del gas en el globo de aire caliente que se muestra al inicio de este capítulo es mayor, menor o igual a la de la atmósfera exterior del globo?
A una presión de 1 atm y una temperatura de 20 °C, el aire seco tiene una densidad de 1.2256 g/L ¿Cuál es la masa molar (promedio) del aire seco?
La temperatura promedio del gas en un globo de aire caliente es de 1.30 × 10 ² °F. Calcule su densidad, asumiendo que la masa molar es igual a la del aire seco.
La capacidad de elevación de un globo de aire caliente es igual a la diferencia en la masa del aire frío desplazado por el globo y la masa del gas en el globo. ¿Cuál es la diferencia en la masa de 1.00 L del aire frío en la parte (c) y el aire caliente en la parte (d)?
Un balón promedio tiene un diámetro de 60 pies y un volumen de 1.1 × 10 ⁵ pies ³. ¿Cuál es el poder de elevación de un globo así? Si el peso del globo y su aparejo es de 500 libras, ¿cuál es su capacidad para transportar pasajeros y carga?
Un globo transporta 40.0 galones de propano líquido (densidad 0.5005 g/L). ¿Qué volumen de gas CO ₂ _{y H 2} O se produce por la combustión de este propano?
Un vuelo en globo puede durar unos 90 minutos. Si todo el combustible se quema durante este tiempo, ¿cuál es la tasa aproximada de pérdida de calor (en kJ/min) del aire caliente en la bolsa durante el vuelo?

S9.5.1

(a) igual; (b) menor que; (c) 29.48 g mol ⁻¹; (d) 1.0966 g L ⁻¹; (e) 0.129 g/L; (f) 4.01 × 10 ⁵ g; capacidad neta de elevación = 384 lb; (g) 270 L; (h) 39.1 kJ min ⁻¹

Q9.5.1

Mostrar que la relación de la tasa de difusión del Gas 1 a la velocidad de difusión del Gas 2,\(\dfrac{R_1}{R_2}\), es la misma a 0 °C y 100 °C.

9.6: Comportamiento de gas no ideal

Q9.6.1

A continuación se muestran gráficos que muestran el comportamiento de varios gases diferentes. ¿Cuáles de estos gases presentan un comportamiento significativamente diferente al esperado para los gases ideales?

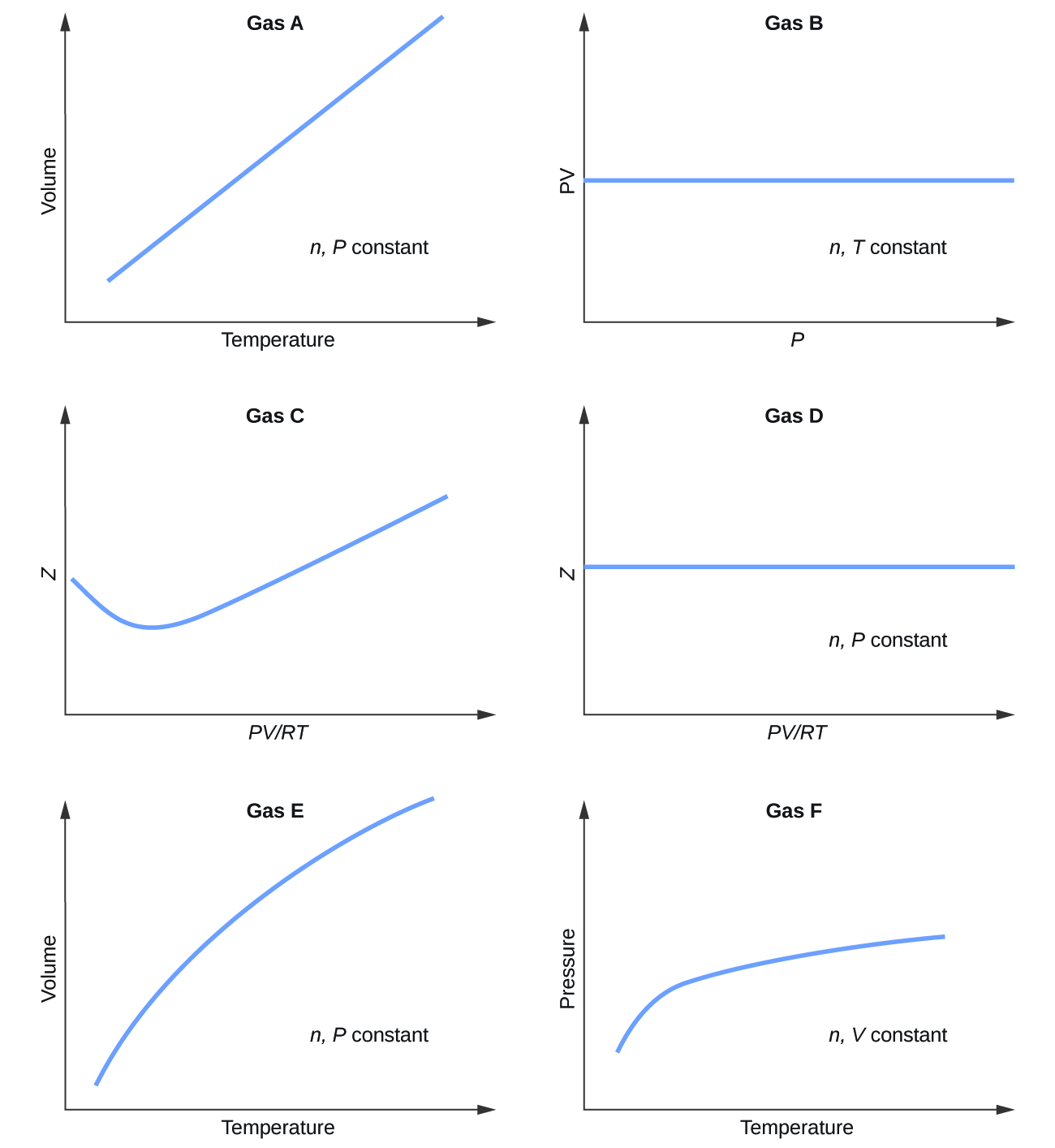
S9.6.1

Gases C, E y F

Q9.6.3

Explicar por qué la parcela de PV para CO ₂ difiere de la de un gas ideal.

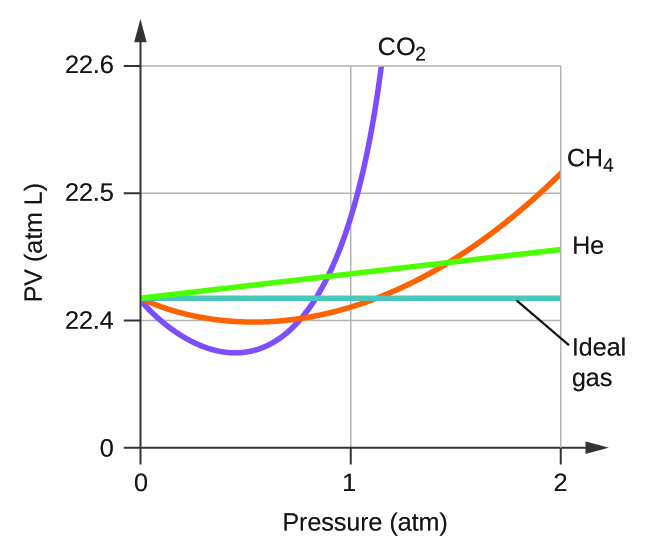
Q9.6.3

¿Bajo cuál de los siguientes conjuntos de condiciones un gas real se comporta más como un gas ideal, y para qué condiciones se espera que un gas real se desvíe del comportamiento ideal? Explique.

alta presión, pequeño volumen
alta temperatura, baja presión
baja temperatura, alta presión

S9.6.3

El comportamiento del gas más parecido a un gas ideal ocurrirá bajo las condiciones en (b). Las moléculas tienen altas velocidades y se mueven a través de mayores distancias entre colisión; también tienen tiempos de contacto más cortos y las interacciones son menos probables. Las desviaciones ocurren con las condiciones descritas en (a) y (c). En las condiciones de (a), algunos gases pueden licuarse. En las condiciones de (c), la mayoría de los gases se licuarán.

Q9.6.4

Describir los factores responsables de la desviación del comportamiento de los gases reales del de un gas ideal.

Q9.6.5

Para cuál de los siguientes gases debe ser mayor la corrección para el volumen molecular: CO, CO ₂, H ₂, He, NH ₃, SF ₆?

S9.6.6

SF ₆

Q9.6.7

Un matraz de 0.245 litros contiene 0.467 mol de CO ₂ a 159 °C. Calcular la presión:

usando la ley de gas ideal
usando la ecuación de van der Waals
Explique el motivo de la diferencia.
Identificar qué corrección (que para P o V) es dominante y por qué.

Q9.6.8

Responde las siguientes preguntas:

Si XX se comportara como un gas ideal, ¿cómo sería su gráfica de Z vs P?
Durante la mayor parte de este capítulo, realizamos cálculos tratando los gases como ideales. ¿Estaba esto justificado?
¿Cuál es el efecto del volumen de moléculas de gas en la Z? ¿Bajo qué condiciones es pequeño este efecto? ¿Cuándo es grande? Explique usando un diagrama apropiado.
¿Cuál es el efecto de las atracciones intermoleculares en el valor de Z? ¿Bajo qué condiciones es pequeño este efecto? ¿Cuándo es grande? Explique usando un diagrama apropiado.
En general, ¿bajo qué condiciones de temperatura esperarías que Z tuviera las mayores desviaciones de la Z para un gas ideal?

S9.6.8

(a) Una línea horizontal recta a 1.0; (b) Cuando los gases reales están a bajas presiones y altas temperaturas se comportan lo suficientemente cerca de los gases ideales como para aproximarse como tales, sin embargo, en algunos casos, vemos que a alta presión y temperatura, la aproximación de gas ideal se descompone y es significativamente diferente a la presión calculada por la ecuación de van der Waals (c) Cuanto mayor sea la compresibilidad, más importa el volumen. A bajas presiones, el factor de corrección para las atracciones intermoleculares es más significativo, y el efecto del volumen de las moléculas de gas en Z sería una pequeña compresibilidad decreciente. A presiones más altas, el efecto del volumen de las propias moléculas de gas sobre Z aumentaría la compresibilidad (ver Figura) (d) Una vez más, a bajas presiones, el efecto de las atracciones intermoleculares sobre Z sería más importante que el factor de corrección para el volumen de las moléculas de gas ellos mismos, aunque quizás todavía pequeños. A presiones más altas y bajas temperaturas, el efecto de las atracciones intermoleculares sería mayor. Ver Figura. e) bajas temperaturas

9.6: Comportamiento de gas no ideal

Ejercicios

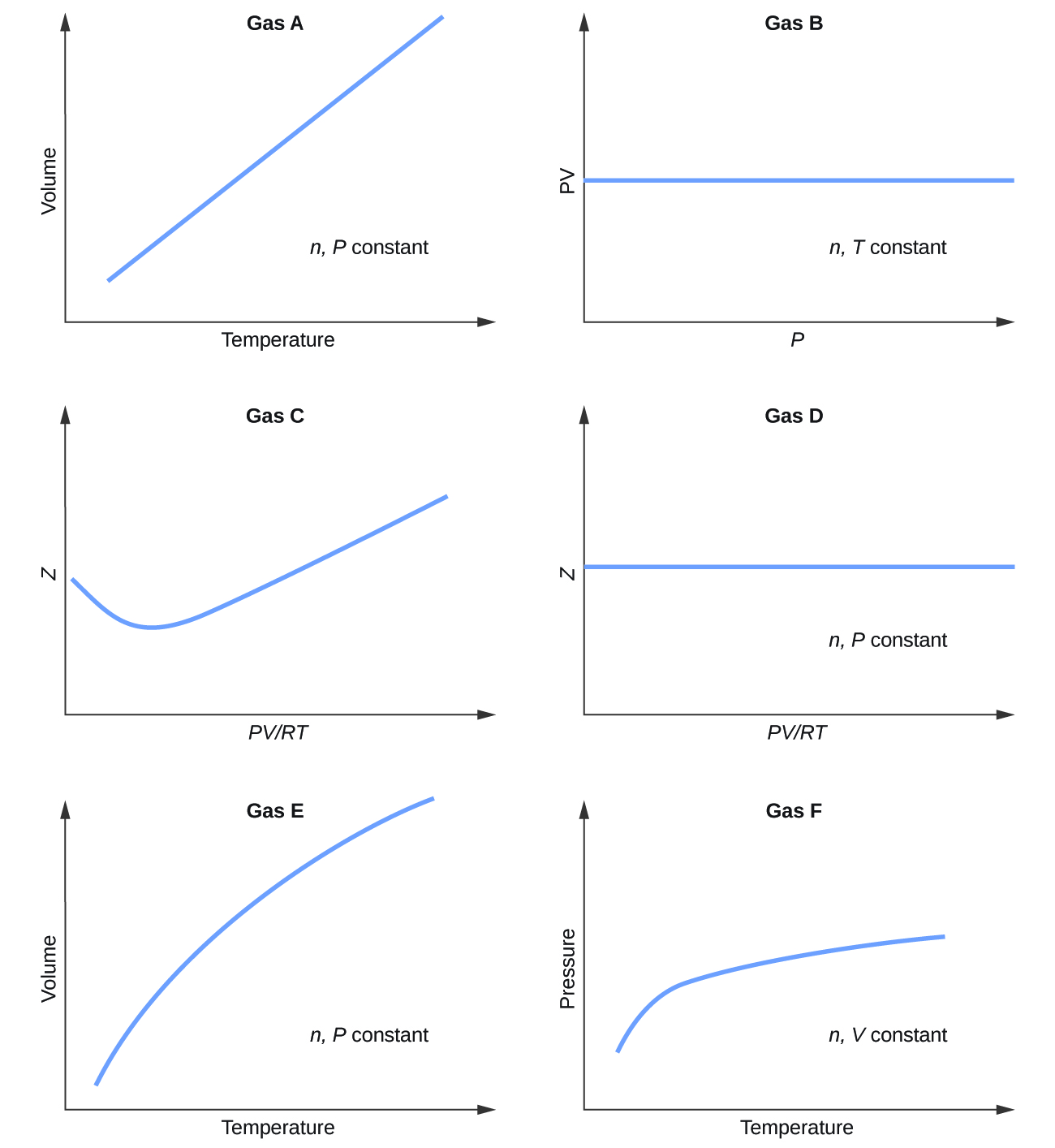
Gases C, E y F

Explicar por qué la parcela de PV para CO ₂ difiere de la de un gas ideal.

(a) alta presión, pequeño volumen

(b) alta temperatura, baja presión

Describir los factores responsables de la desviación del comportamiento de los gases reales del de un

gas ideal.

Para cuál de los siguientes gases debe ser mayor la corrección para el volumen molecular:

CO, CO ₂, H ₂, He, NH ₃, SF ₆?

SF ₆

Un matraz de 0.245 litros contiene 0.467 mol de CO ₂ a 159 °C. Calcular la presión:

(a) usar la ley de gas ideal

(b) usando la ecuación de van der Waals

c) Explicar el motivo de la diferencia.

d) Identificar qué corrección (la de P o V) es dominante y por qué.

Responde las siguientes preguntas:

(a) Si XX se comportara como un gas ideal, ¿cómo sería su gráfica de Z vs. P?

(b) Para la mayor parte de este capítulo, realizamos cálculos tratando los gases como ideales. ¿Estaba esto justificado?

c) ¿Cuál es el efecto del volumen de moléculas de gas en Z? ¿Bajo qué condiciones es pequeño este efecto? ¿Cuándo es grande? Explique usando un diagrama apropiado.

d) ¿Cuál es el efecto de las atracciones intermoleculares sobre el valor de Z? ¿Bajo qué condiciones es pequeño este efecto? ¿Cuándo es grande? Explique usando un diagrama apropiado.

(e) En general, ¿en qué condiciones de temperatura esperaría que Z tuviera las mayores desviaciones de la Z para un gas ideal?