14.4: Hidrólisis de Soluciones Salinas

Objetivos de aprendizaje

• Predecir si una solución salina será ácida, básica o neutra
• Calcular las concentraciones de las diversas especies en una solución salina
• Describir el proceso que hace que las soluciones de ciertos iones metálicos sean ácidas

Como hemos visto en el apartado de reacciones químicas, cuando se mezclan un ácido y una base, se someten a una reacción de neutralización. La palabra “neutralización” parece implicar que una solución estequiométricamente equivalente de un ácido y una base sería neutra. Esto a veces es cierto, pero las sales que se forman en estas reacciones pueden tener propiedades ácidas o básicas propias, como veremos ahora.

Neutralización ácido-base

Una solución es neutra cuando contiene concentraciones iguales de iones hidronio e hidróxido. Cuando mezclamos soluciones de un ácido y una base, se produce una reacción de neutralización ácido-base. Sin embargo, aunque mezclemos cantidades estequiométricamente equivalentes, podemos encontrar que la solución resultante no es neutra. Podría contener un exceso de iones hidronio o un exceso de iones hidróxido porque la naturaleza de la sal formada determina si la solución es ácida, neutra o básica. Las siguientes cuatro situaciones ilustran cómo pueden surgir soluciones con diversos valores de pH después de una reacción de neutralización usando cantidades estequiométricamente equivalentes:

1. Un ácido fuerte y una base fuerte, tales como HCl (ac) y NaOH (ac) reaccionarán para formar una solución neutra ya que los socios conjugados producidos son de fuerza insignificante:\[\ce{HCl}(aq)+\ce{NaOH}(aq)⇌\ce{NaCl}(aq)+\ce{H2O}(l) \nonumber \]
2. Un ácido fuerte y una base débil producen una solución débilmente ácida, no por el ácido fuerte involucrado, sino por el ácido conjugado de la base débil.
3. Un ácido débil y una base fuerte producen una solución débilmente básica. Una solución de un ácido débil reacciona con una solución de una base fuerte para formar la base conjugada del ácido débil y el ácido conjugado de la base fuerte. El ácido conjugado de la base fuerte es un ácido más débil que el agua y no tiene ningún efecto sobre la acidez de la solución resultante. Sin embargo, la base conjugada del ácido débil es una base débil e ioniza ligeramente en agua. Esto aumenta la cantidad de ion hidróxido en la solución producida en la reacción y la vuelve ligeramente básica.
4. Un ácido débil más una base débil pueden producir una solución ácida, básica o neutra. Este es el más complejo de los cuatro tipos de reacciones. Cuando el ácido conjugado y la base conjugada son de resistencias desiguales, la solución puede ser ácida o básica, dependiendo de las fuerzas relativas de los dos conjugados. Ocasionalmente el ácido débil y la base débil tendrán la misma fuerza, por lo que su respectiva base conjugada y ácido tendrán la misma fuerza, y la solución será neutra. Para predecir si una combinación particular será ácida, básica o neutra, se deben comparar los valores de K tabulados de los conjugados.

Antiácidos Estómagos

Nuestros estómagos contienen una solución de aproximadamente 0.03 M HCl, lo que nos ayuda a digerir los alimentos que comemos. La sensación de ardor asociada con la acidez estomacal es el resultado de que el ácido del estómago se escapa a través de la válvula muscular en la parte superior del estómago hacia los tramos inferiores del esófago. El revestimiento del esófago no está protegido de los efectos corrosivos del ácido estomacal como está el revestimiento del estómago, y los resultados pueden ser muy dolorosos. Cuando tenemos acidez estomacal, se siente mejor si reducimos el exceso de ácido en el esófago tomando un antiácido. Como habrás adivinado, los antiácidos son bases. Uno de los antiácidos más comunes es el carbonato de calcio, CaCo ₃. La reacción,

\[CaCO_3(s)+2HCl(aq)⇌CaCl_2(aq)+H_2O(l)+CO_2(g) \nonumber \]

no sólo neutraliza el ácido estomacal, también produce CO ₂ (g), lo que puede resultar en un eructo satisfactorio.

Leche de Magnesia es una suspensión de la base escasamente soluble hidróxido de magnesio, Mg (OH) ₂. Funciona de acuerdo a la reacción:

\[Mg(OH)_2(s)⇌Mg^{2+}(aq)+2OH^-(aq) \nonumber \]

Los iones hidróxido generados en este equilibrio luego pasan a reaccionar con los iones hidronio del ácido estomacal, de manera que:

\[H_3O^+ + OH^- ⇌ 2H_2O(l) \nonumber \]

Esta reacción no produce dióxido de carbono, pero los antiácidos que contienen magnesio pueden tener un efecto laxante. Varios antiácidos tienen hidróxido de aluminio, Al (OH) ₃, como ingrediente activo. El hidróxido de aluminio tiende a causar estreñimiento, y algunos antiácidos utilizan hidróxido de aluminio en concierto con hidróxido de magnesio para equilibrar los efectos secundarios de las dos sustancias.

Aspectos culinarios de la química

Cocinar es esencialmente química sintética que resulta ser segura para comer. Hay una serie de ejemplos de química ácido-base en el mundo culinario. Un ejemplo es el uso de bicarbonato de sodio, o bicarbonato de sodio en la cocción. NaHCo ₃ es una base. Cuando reacciona con un ácido como jugo de limón, suero de leche o crema agria en una masa, se forman burbujas de gas dióxido de carbono a partir de la descomposición del ácido carbónico resultante, y la masa “sube”. El polvo de hornear es una combinación de bicarbonato de sodio y una o más sales ácidas que reaccionan cuando los dos productos químicos entran en contacto con el agua de la masa.

A mucha gente le gusta poner jugo de limón o vinagre, ambos ácidos, sobre el pescado cocido (Figura\(\PageIndex{1}\)). Resulta que los peces tienen aminas volátiles (bases) en sus sistemas, las cuales son neutralizadas por los ácidos para producir sales de amonio no volátiles. Esto reduce el olor del pescado, y además agrega un sabor “agrio” que parece que disfrutamos.

Figura\(\PageIndex{1}\): Se produce una reacción de neutralización entre el ácido cítrico en los limones o el ácido acético en vinagre, y las bases en la carne de pescado.

El decapado es un método utilizado para conservar vegetales utilizando un ambiente ácido producido naturalmente. La verdura, como un pepino, se coloca en un frasco sellado sumergido en una solución de salmuera. La solución de salmuera favorece el crecimiento de bacterias beneficiosas y suprime el crecimiento de bacterias dañinas. Las bacterias beneficiosas se alimentan de almidones en el pepino y producen ácido láctico como producto de desecho en un proceso llamado fermentación. El ácido láctico eventualmente aumenta la acidez de la salmuera a un nivel que mata cualquier bacteria dañina, que requiere un ambiente básico. Sin las bacterias dañinas que consumen los pepinos pueden durar mucho más tiempo que si estuvieran desprotegidos. Un subproducto del proceso de decapado cambia el sabor de las verduras con el ácido haciéndolas un sabor agrio.

Sales de Bases Débiles y Ácidos Fuertes

Cuando neutralizamos una base débil con un ácido fuerte, el producto es una sal que contiene el ácido conjugado de la base débil. Este ácido conjugado es un ácido débil. Por ejemplo, el cloruro amónico, NH ₄ Cl, es una sal formada por la reacción del amoníaco base débil con el ácido fuerte HCl:

\[\ce{NH3}(aq)+\ce{HCl}(aq)⟶\ce{NH4Cl}(aq) \nonumber \]

Una solución de esta sal contiene iones amonio e iones cloruro. El ion cloruro no tiene efecto sobre la acidez de la solución ya que el HCl es un ácido fuerte. El cloruro es una base muy débil y no aceptará un protón en una medida medible. Sin embargo, el ion amonio, el ácido conjugado del amoníaco, reacciona con el agua y aumenta la concentración de iones hidronio:

\[\ce{NH4+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{NH3}(aq) \nonumber \]

La ecuación de equilibrio para esta reacción es simplemente la constante de ionización. K _a, para el ácido\(\ce{NH4+}\):

\[\ce{\dfrac{[H3O+][NH3]}{[NH4+]}}=K_\ce{a} \nonumber \]

_{No encontraremos un valor de K a para el ión amonio en la Tabla E1.} Sin embargo, no es difícil determinar K _a\(\ce{NH4+}\) partir del valor de la constante de ionización del agua, K _w, y K _b, la constante de ionización de su base conjugada, NH ₃, usando la siguiente relación:

\[K_\ce{w}=K_\ce{a}×K_\ce{b} \nonumber \]

Esta relación se mantiene para cualquier base y su ácido conjugado o para cualquier ácido y su base conjugada.

Ejemplo\(\PageIndex{1}\): pH of a Solution of a Salt of a Weak Base and a Strong Acid

La anilina es una amina que se utiliza para fabricar tintes. Se aísla como clorhidrato de anilina\(\ce{[C6H5NH3+]Cl}\), una sal preparada por la reacción de la base débil anilina y ácido clorhídrico. ¿Cuál es el pH de una solución 0.233 M de clorhidrato de anilina?

\[\ce{C6H5NH3+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{C6H5NH2}(aq) \nonumber \]

Solución

El nuevo paso en este ejemplo es determinar K _a para el\(\ce{C6H5NH3+}\) ion. El\(\ce{C6H5NH3+}\) ion es el ácido conjugado de una base débil. El valor de K _a para este ácido no está listado en la Tabla E1, pero podemos determinarlo a partir del valor de K _b para anilina, C ₆ H ₅ NH ₂, que se da como 4.6 × 10 ⁻¹⁰:

\[\mathrm{\mathit{K}_a(for\:C_6H_5NH_3^+)×\mathit{K}_b(for\:C_6H_5NH_2)=\mathit{K}_w=1.0×10^{−14}} \nonumber \]

\[\mathrm{\mathit{K}_a(for\:C_6H_5NH_3^+)=\dfrac{\mathit{K}_w}{\mathit{K}_b(for\:C_6H_5NH_2)}=\dfrac{1.0×10^{−14}}{4.6×10^{−10}}=2.3×10^{−5}} \nonumber \]

Ahora tenemos la constante de ionización y la concentración inicial del ácido débil, la información necesaria para determinar la concentración de equilibrio de H ₃ O ⁺, y el pH:

 

Se muestran cuatro rectángulos bronceados que están conectados con flechas que apuntan hacia la derecha. El primero está etiquetado como “Determinar la dirección del cambio”. El segundo está etiquetado como “Determinar x y las concentraciones de equilibrio”. El tercero está etiquetado como “Resolver para x y las concentraciones de equilibrio”. El cuarto está etiquetado como “Verifica las matemáticas”.

Con estos pasos encontramos [H ₃ O ⁺] = 2.3 × 10 ⁻³ M y pH = 2.64

Ejercicio\(\PageIndex{1}\)

1. Haga los cálculos y muestre que la concentración de iones hidronio para una solución 0.233- M de\(\ce{C6H5NH3+}\) es 2.3 × 10 ⁻³ y el pH es 2.64.
2. Cuál es la concentración de iones hidronio en una solución 0.100- M de nitrato de amonio, NH ₄ NO ₃, una sal compuesta por los iones\(\ce{NH4+}\) y\(\ce{NO3-}\). Utilice los datos de la Tabla E1 para determinar K _b para el ión amonio. ¿Cuál es el ácido más fuerte\(\ce{C6H5NH3+}\) o\(\ce{NH4+}\)?

Contestar a

\(K_a\ce{(for\:NH4+)}=5.6×10^{−10}\), [H ₃ O ⁺] = 7.5 × 10−6 M

Respuesta b

\(\ce{C6H5NH3+}\)es el ácido más fuerte (a) (b).

Sales de Ácidos Débiles y Bases Fuertes

Cuando neutralizamos un ácido débil con una base fuerte, obtenemos una sal que contiene la base conjugada del ácido débil. Esta base conjugada suele ser una base débil. Por ejemplo, el acetato de sodio, _{NaCh 3} CO ₂, es una sal formada por la reacción del ácido acético ácido débil con la base fuerte hidróxido de sodio:

\[\ce{CH3CO2H}(aq)+\ce{NaOH}(aq)⟶\ce{NaCH3CO2}(aq)+\ce{H2O}(aq) \nonumber \]

Una solución de esta sal contiene iones sodio e iones acetato. El ion sodio no tiene efecto sobre la acidez de la solución. Sin embargo, el ion acetato, la base conjugada del ácido acético, reacciona con el agua y aumenta la concentración de ión hidróxido:

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \nonumber \]

La ecuación de equilibrio para esta reacción es la constante de ionización, K _b, para la base\(\ce{CH3CO2-}\). El valor de K _b se puede calcular a partir del valor de la constante de ionización del agua, K _w, y K _a, la constante de ionización del ácido conjugado del anión usando la ecuación:

\[_\ce{w}=K_\ce{a}×K_\ce{b} \nonumber \]

Para el ion acetato y su ácido conjugado tenemos:

\[\mathrm{\mathit{K}_b(for\:\ce{CH_3CO_2^-})=\dfrac{\mathit{K}_w}{\mathit{K}_a(for\:CH_3CO_2H)}=\dfrac{1.0×10^{−14}}{1.8×10^{−5}}=5.6×10^{−10}} \nonumber \]

Algunos manuales no reportan valores de K _b. Solo reportan constantes de ionización para ácidos. _{Si queremos determinar un valor de K b utilizando uno de estos manuales, debemos buscar el valor de K a para el ácido conjugado y convertirlo en un valor de K b.}

Ejemplo\(\PageIndex{2}\): Equilibrium of a Salt of a Weak Acid and a Strong Base

Determinar la concentración de ácido acético en una solución con\(\ce{[CH3CO2- ]}=0.050\:M\) y [OH ⁻] = 2.5 × 10 ⁻⁶ M en equilibrio. La reacción es:

\[\ce{CH3CO2-}(aq)+\ce{H2O}(l)⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) \nonumber \]

Solución

Se nos dan dos de las tres concentraciones de equilibrio y se nos pide encontrar la concentración faltante. Si podemos encontrar la constante de equilibrio para la reacción, el proceso es sencillo.

El ion acetato se comporta como base en esta reacción; los iones hidróxido son un producto. Determinamos K _b de la siguiente manera:

\[\mathrm{\mathit{K}_b(for\:\ce{CH_3CO_2^-})=\dfrac{\mathit{K}_w}{\mathit{K}_a(for\:CH_3CO_2H)}=\dfrac{1.0×10^{−14}}{1.8×10^{−5}}=5.6×10^{−10}} \nonumber \]

Ahora encuentra la concentración faltante:

\[K_\ce{b}=\ce{\dfrac{[CH3CO2H][OH- ]}{[CH3CO2- ]}}=5.6×10^{−10} \nonumber \]

\[=\dfrac{[\ce{CH3CO2H}](2.5×10^{−6})}{(0.050)}=5.6×10^{−10} \nonumber \]

Resolviendo esta ecuación obtenemos [CH ₃ CO ₂ H] = 1.1 × 10 ⁻⁵ M.

Ejercicio\(\PageIndex{2}\)

¿Cuál es el pH de una solución 0.083- M de CN ⁻? Use 4.9 × 10 ⁻¹⁰ como K _a para HCN. Pista: Probablemente necesitaremos convertir PoH a pH o encontrar [H ₃ O ⁺] usando [OH ⁻] en las etapas finales de este problema.

Responder

11.16

Equilibrio en una Solución de una Sal de un Ácido Débil y una Base Débil

En una solución de una sal formada por la reacción de un ácido débil y una base débil, para predecir el pH, debemos conocer tanto la K _a del ácido débil como la K _b de la base débil. Si K _a > K _b, la solución es ácida, y si K _b > K _a, la solución es básica.

Ejemplo\(\PageIndex{3}\): Determining the Acidic or Basic Nature of Salts

Determinar si las soluciones acuosas de las siguientes sales son ácidas, básicas o neutras:

1. KBr
2. NaHCo ₃
3. NH ₄ Cl
4. Na ₂ HPO ₄
5. NH ₄ F

Solución

Considere cada uno de los iones por separado en términos de su efecto sobre el pH de la solución, como se muestra aquí:

1. El catión K ⁺ y el anión Br ⁻ son ambos espectadores, ya que son el catión de una base fuerte (KOH) y el anión de un ácido fuerte (HBr), respectivamente. La solución es neutra.
2. _{El catión Na ⁺ es un espectador, y no afectará el pH de la solución; el\(\ce{HCO3-}\) anión es anfiprótico.El K a de\(\ce{HCO3-}\) es 4.7 × 10 ⁻¹¹, por lo que el K b de su base conjugada es\(\dfrac{1.0×10^{−14}}{4.7×10^{−11}}=2.1×10^{−4}\).} Desde K _b >> K _a, la solución es básica.
3. El\(\ce{NH4+}\) ion es ácido y el ion Cl ⁻ es un espectador. La solución será ácida.
4. El ion Na ⁺ es un espectador y no afectará el pH de la solución, mientras que el\(\ce{HPO4^{2-}}\) ion es anfiprótico. La K _a de\(\ce{HPO_4^{2-}}\) es 4.2 × 10 ⁻¹³ y su K _b es\(\dfrac{1.0×10^{−14}}{4.2×10^{−13}}=2.4×10^{−2}\). Debido a que K _b >> K _a, la solución es básica.
5. El\(\ce{NH4+}\) ion se enumera como ácido, y el ion F ⁻ aparece como base, por lo que debemos comparar directamente el K _a y el K _b de los dos iones. K _a de\(\ce{NH4+}\) es 5.6 × 10 ⁻¹⁰, lo que parece muy pequeño, sin embargo el K _b de F ⁻ es 1.4 × 10 ⁻¹¹, por lo que la solución es ácida, ya que K _a > K _b.

Ejercicio\(\PageIndex{3}\)

Determinar si las soluciones acuosas de las siguientes sales son ácidas, básicas o neutras:

1. K ₂ CO ₃
2. CaCl ₂
3. KH ₂ PO ₄
4. (NH ₄) ₂ CO ₃
5. AlBr ₃

Contestar a

básico

Respuesta b

neutral

Respuesta c

ácido

Respuesta d

básico

Respuesta e

ácido

La ionización de iones metálicos hidratados

Si medimos el pH de las soluciones de una variedad de iones metálicos encontraremos que estos iones actúan como ácidos débiles cuando están en solución. El ion aluminio es un ejemplo. Cuando el nitrato de aluminio se disuelve en agua, el ion aluminio reacciona con el agua para dar un ion de aluminio hidratado\(\ce{Al(H2O)6^3+}\), disuelto en agua a granel. Lo que esto significa es que el ion aluminio tiene las interacciones más fuertes con las seis moléculas de agua más cercanas (la llamada primera capa de solvatación), a pesar de que también interactúa con las otras moléculas de agua que rodean este\(\ce{Al(H2O)6^3+}\) cúmulo:

\[\ce{Al(NO3)3}(s)+\ce{6H2O}(l)⟶\ce{Al(H2O)6^3+}(aq)+\ce{3NO3-}(aq) \nonumber \]

Frecuentemente vemos la fórmula de este ion simplemente como “Al ^{3 +} (aq)”, sin señalar explícitamente las seis moléculas de agua que son las más cercanas al ion aluminio y solo describimos el ion como solvatado en agua (hidratado). Esto es similar a la simplificación de la fórmula del ion hidronio, H ₃ O ⁺ a H ⁺. Sin embargo, en este caso, el ion aluminio hidratado es un ácido débil (Figura\(\PageIndex{2}\)) y dona un protón a una molécula de agua. Así, la hidratación cobra importancia y podemos usar fórmulas que muestren el grado de hidratación:

\[\ce{Al(H2O)6^3+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Al(H2O)5(OH)^2+}(aq) \hspace{20px} K_\ce{a}=1.4×10^{−5} \nonumber \]

Al igual que con otros ácidos polipróticos, el ion aluminio hidratado se ioniza en etapas, como se muestra por:

\[\ce{Al(H2O)6^3+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Al(H2O)5(OH)^2+}(aq) \nonumber \]

\[\ce{Al(H2O)5(OH)^2+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Al(H2O)4(OH)2+}(aq) \nonumber \]

\[\ce{Al(H2O)4(OH)2+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Al(H2O)3(OH)3}(aq) \nonumber \]

Nótese que algunas de estas especies de aluminio están exhibiendo un comportamiento anfiprótico, ya que están actuando como ácidos cuando aparecen en el lado izquierdo de las expresiones de equilibrio y como bases cuando aparecen en el lado derecho.

Figura\(\PageIndex{2}\): Cuando un ion aluminio reacciona con el agua, el ion aluminio hidratado se convierte en un ácido débil.

Se muestra una reacción usando modelos de bola y palo. A la izquierda, entre corchetes con un superíndice de 3 más afuera a la derecha está la estructura etiquetada como “[A l (H subíndice 2 O) subíndice 6] superíndice 3 más”. Dentro de los corchetes se encuentra el átomo gris central al que se unen 6 átomos rojos en una disposición que los distribuye uniformemente alrededor del átomo gris central. Cada átomo rojo tiene dos átomos blancos más pequeños unidos en una disposición bifurcada o doblada. Fuera de los soportes a la derecha hay un modelo de relleno de espacio que incluye una esfera central roja con dos esferas blancas más pequeñas unidas en una disposición doblada. Debajo de esta estructura se encuentra la etiqueta “H subíndice 2 O.” Sigue una flecha de doble cara. Otro conjunto de corchetes sigue a la derecha de las flechas que tienen un superíndice de dos más afuera a la derecha. La estructura dentro de los corchetes es similar a la de la izquierda, excepto que se elimina un átomo blanco de la estructura. La siguiente etiqueta también se cambia a “[A l (H subíndice 2 O) subíndice 5 O H] superíndice 2 más”. A la derecha de esta estructura y fuera de los soportes se encuentra un modelo de relleno de espacio con una esfera roja central a la que se unen 3 esferas blancas más pequeñas. Esta estructura está etiquetada como “H subíndice 3 O superíndice más”.

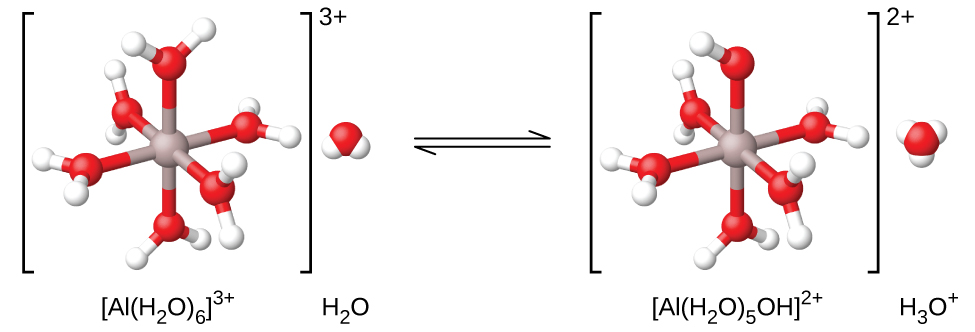
Sin embargo, la ionización de un catión que porta más de una carga no suele ser extensa más allá de la primera etapa. Ejemplos adicionales de la primera etapa en la ionización de iones metálicos hidratados son:

\[\ce{Fe(H2O)6^3+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Fe(H2O)5(OH)^2+}(aq) \hspace{20px} K_\ce{a}=2.74 \nonumber \]

\[\ce{Cu(H2O)6^2+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Cu(H2O)5(OH)+}(aq) \hspace{20px} K_\ce{a}=~6.3 \nonumber \]

\[\ce{Zn(H2O)4^2+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Zn(H2O)3(OH)+}(aq) \hspace{20px} K_\ce{a}=9.6 \nonumber \]

Ejemplo\(\PageIndex{4}\): Hydrolysis of [Al(H₂O)₆]³⁺

Calcular el pH de una solución 0.10- M de cloruro de aluminio, que se disuelve completamente para dar el ion aluminio hidratado\(\ce{[Al(H2O)6]^3+}\) en solución.

Solución

A pesar de la apariencia inusual del ácido, este es un problema típico de ionización ácida.

 

Se muestra una reacción usando modelos de bola y palo. A la izquierda, entre corchetes con un superíndice de 3 más afuera a la derecha está la estructura etiquetada como “[A l (H subíndice 2 O) subíndice 6] superíndice 3 más”. Dentro de los corchetes se encuentra el átomo gris central al que se unen 6 átomos rojos en una disposición que los distribuye uniformemente alrededor del átomo gris central. Cada átomo rojo tiene dos átomos blancos más pequeños unidos en una disposición bifurcada o doblada. Fuera de los soportes a la derecha hay un modelo de relleno de espacio que incluye una esfera central roja con dos esferas blancas más pequeñas unidas en una disposición doblada. Debajo de esta estructura se encuentra la etiqueta “H subíndice 2 O.” Sigue una flecha de doble cara. Otro conjunto de corchetes sigue a la derecha de las flechas que tienen un superíndice de dos más afuera a la derecha. La estructura dentro de los corchetes es similar a la de la izquierda, excepto que se elimina un átomo blanco de la estructura. La siguiente etiqueta también se cambia a “[A l (H subíndice 2 O) subíndice 5 O H] superíndice 2 más”. A la derecha de esta estructura y fuera de los soportes se encuentra un modelo de relleno de espacio con una esfera roja central a la que se unen 3 esferas blancas más pequeñas. Esta estructura está etiquetada como “H subíndice 3 O superíndice más”.

1. Determinar la dirección del cambio. La ecuación para la reacción y K _a son:

   \(\ce{Al(H2O)6^3+}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{Al(H2O)5(OH)^2+}(aq) \hspace{20px} K_\ce{a}=1.4×10^{−5}\)

   La reacción se desplaza hacia la derecha para alcanzar el equilibrio.
2. Determinar x y concentraciones de equilibrio. Usa la mesa

:

Esta tabla tiene dos columnas principales y cuatro filas. La primera fila para la primera columna no tiene encabezamiento y luego tiene lo siguiente en la primera columna: Concentración inicial (M), Cambio (M), Concentración en equilibrio (M). La segunda columna tiene el encabezado de “A l (H subíndice 2 O) subíndice 6 superíndice 3 signo positivo más H subíndice 2 O flecha de equilibrio H subíndice 3 O superíndice signo positivo más A l (H subíndice 2 O) subíndice 5 (O H) superíndice 2 signo positivo”. Debajo de la segunda columna hay un subgrupo de cuatro columnas y tres filas. La primera columna tiene lo siguiente: 0.10 (que aparece en rojo), x negativo, 0.10 menos x La segunda columna está en blanco. La tercera columna tiene lo siguiente: aproximadamente 0, x, x. La cuarta columna tiene lo siguiente: 0, x, x.

Resolver para x y las concentraciones de equilibrio. Sustituyendo las expresiones por las concentraciones de equilibrio en la ecuación para la constante de ionización produce:

1. \[K_\ce{a}=\ce{\dfrac{[H3O+][Al(H2O)5(OH)^2+]}{[Al(H2O)6^3+]}} \nonumber \]

   \(=\dfrac{(x)(x)}{0.10−x}=1.4 \times 10^{−5}\)

   Solving this equation gives:

   \[x=1.2×10^{−3}\:M \nonumber \]

   From this we find:

   \[\ce{[H3O+]}=0+x=1.2×10^{−3}\:M \nonumber \]

   \[\mathrm{pH=−log[H_3O^+]=2.92(an\: acidic\: solution)} \nonumber \]

   Check the work. The arithmetic checks; when 1.2 × 10⁻³ M is substituted for x, the result = K_a.

Exercise \(\PageIndex{4}\)

What is \(\ce{[Al(H2O)5(OH)^2+]}\) in a 0.15-M solution of Al(NO₃)₃ that contains enough of the strong acid HNO₃ to bring [H₃O⁺] to 0.10 M?

Answer

2.1 × 10⁻⁵ M

The constants for the different stages of ionization are not known for many metal ions, so we cannot calculate the extent of their ionization. However, practically all hydrated metal ions other than those of the alkali metals ionize to give acidic solutions. Ionization increases as the charge of the metal ion increases or as the size of the metal ion decreases.

Summary

The characteristic properties of aqueous solutions of Brønsted-Lowry acids are due to the presence of hydronium ions; those of aqueous solutions of Brønsted-Lowry bases are due to the presence of hydroxide ions. The neutralization that occurs when aqueous solutions of acids and bases are combined results from the reaction of the hydronium and hydroxide ions to form water. Some salts formed in neutralization reactions may make the product solutions slightly acidic or slightly basic. Solutions that contain salts or hydrated metal ions have a pH that is determined by the extent of the hydrolysis of the ions in the solution. The pH of the solutions may be calculated using familiar equilibrium techniques, or it may be qualitatively determined to be acidic, basic, or neutral depending on the relative K_a and K_b of the ions involved.