14.E: Equilibrios ácido-base (Ejercicios)

14.1: Ácidos y bases de Brønsted-Lowry

Q14.1.1

Escribir ecuaciones que muestren NH ₃ tanto como un ácido conjugado como una base conjugada.

S14.1.1

Un ejemplo para NH ₃ como un ácido conjugado:\(\ce{NH2- + H+ ⟶ NH3}\); como base conjugada:\(\ce{NH4+}(aq)+\ce{OH-}(aq)⟶\ce{NH3}(aq)+\ce{H2O}(l)\)

Q14.1.2

Escribir ecuaciones que muestren\(\ce{H2PO4-}\) actuar tanto como ácido como base.

Q14.1.3

Demostrar mediante ecuaciones iónicas netas adecuadas que cada una de las siguientes especies puede actuar como un ácido de Brønsted-Lowry:

1. \(\ce{H3O+}\)
2. HCl
3. NH ₃
4. CH ₃ CO ₂ H
5. \(\ce{NH4+}\)
6. \(\ce{HSO4-}\)

S14.1.3

1. \(\ce{H3O+}(aq)⟶\ce{H+}(aq)+ \ce{H_2O}_{(l)}\);
2. \(\ce{HCl}(l)⟶\ce{H+}(aq)+\ce{Cl-}(aq)\);
3. \(\ce{NH3}(aq)⟶\ce{H+}(aq)+\ce{NH2-}(aq)\);
4. \(\ce{CH3CO2H}(aq)⟶\ce{H+}(aq)+\ce{CH3CO2-}(aq)\);
5. \(\ce{NH4+}(aq)⟶\ce{H+}(aq)+\ce{NH3}(aq)\);
6. \(\ce{HSO4-}(aq)⟶\ce{H+}(aq)+\ce{SO4^2-}(aq)\)

Q14.1.4

Demostrar mediante ecuaciones iónicas netas adecuadas que cada una de las siguientes especies puede actuar como un ácido de Brønsted-Lowry:

1. HNO ₃
2. \(\ce{PH4+}\)
3. H ₂ S
4. CH ₃ CH ₂ COOH
5. \(\ce{H2PO4-}\)
6. HS ⁻

Q14.1.5

Demostrar mediante ecuaciones iónicas netas adecuadas que cada una de las siguientes especies puede actuar como una base de Brønsted-Lowry:

1. H ₂ O
2. \(\ce{OH-}\)
3. NH ₃
4. CN ⁻
5. S ²⁻
6. \(\ce{H2PO4-}\)

S14.1.5

1. \(\ce{H_2O}_{(l)} + \ce{H^+} (aq)⟶\ce{H3O+}(aq)\)
2. \(\ce{OH-} (aq) + \ce{H^+} (aq)⟶ \ce{H_2O}_{(l)}\)
3. \(\ce{NH3}(aq) + \ce{H^+} (aq)⟶\ce{NH4+}(aq)\);
4. \(\ce{CN-}(aq) + \ce{H^+} (aq)⟶\ce{HCN}(aq)\)
5. \(\ce{S^2-}(aq) + \ce{H^+} (aq)⟶\ce{HS-}(aq)\)
6. \(\ce{H2PO4-}(aq) + \ce{H^+} (aq)⟶\ce{H3PO4}(aq)\)

Q14.1.6

Demostrar mediante ecuaciones iónicas netas adecuadas que cada una de las siguientes especies puede actuar como una base de Brønsted-Lowry:

1. HS ⁻
2. \(\ce{PO4^3-}\)
3. \(\ce{NH2-}\)
4. C ₂ H ₅ OH
5. O ²⁻
6. \(\ce{H2PO4-}\)

Q14.1.7

¿Cuál es el ácido conjugado de cada uno de los siguientes? ¿Cuál es la base conjugada de cada uno?

1. \(\ce{OH-}\)
2. H ₂ O
3. \(\ce{HCO3-}\)
4. NH ₃
5. \(\ce{HSO4-}\)
6. H ₂ O ₂
7. HS ⁻
8. \(\ce{H5N2+}\)

S14.1.7

H ₂ O, O ²⁻; H ₃ O ⁺,\(\ce{OH^-}\); H ₂ CO ₃,\(\ce{CO3^2-}\);\(\ce{NH4+}\),\(\ce{NH2-}\); H ₂ SO ₄,\(\ce{SO4^2-}\);\(\ce{H3O2+}\),\(\ce{HO2-}\); H ₂ S; S ²⁻;\(\ce{H6N2^2+}\), H ₄ N ₂

Q14.1.8

¿Cuál es el ácido conjugado de cada uno de los siguientes? ¿Cuál es la base conjugada de cada uno?

1. H ₂ S
2. \(\ce{H2PO4-}\)
3. PH ₃
4. HS ⁻
5. \(\ce{HSO3-}\)
6. \(\ce{H3O2+}\)
7. H ₄ N ₂
8. CH ₃ OH

Q14.1.9

Identificar y etiquetar el ácido de Brønsted-Lowry, su base conjugada, la base de Brønsted-Lowry y su ácido conjugado en cada una de las siguientes ecuaciones:

1. \(\ce{HNO3 + H2O ⟶ H3O+ + NO3-}\)
2. \(\ce{CN- + H2O ⟶ HCN + OH-}\)
3. \(\ce{H2SO4 + Cl- ⟶ HCl + HSO4-}\)
4. \(\ce{HSO4- + OH- ⟶ SO4^2- + H2O}\)
5. \(\ce{O^2- + H2O ⟶ 2OH-}\)
6. \(\ce{[Cu(H2O)3(OH)]+ + [Al(H2O)6]^3+ ⟶ [Cu(H2O)4]^2+ + [Al(H2O)5(OH)]^2+}\)
7. \(\ce{H2S + NH2- ⟶ HS- + NH3}\)

S14.1.9

Los marcadores son ácido de Brønsted-Lowry = BA; su base conjugada = CB; base de Brønsted-Lowry = BB; su ácido conjugado = CA. HNO ₃ (BA), H ₂ O (BB), H ₃ O ⁺ (CA),\(\ce{NO3- (CB)}\); CN ⁻ (BB), H ₂ O (BA), HCN (CA),\(\ce{OH^-}\) (CB); H ₂ SO ₄ (BA), Cl ⁻ (BB), HCl (CA),\(\ce{HSO4- (CB)}\);\(\ce{HSO4- (BA)}\), OH ^- (BB)\(\ce{SO4^2- (CB)}\), H ₂ O (CA); O ²⁻ (BB), H2O (BA)\(\ce{OH^-}\) (CB y CA); [Cu (H ₂ O) ₃ (OH)] ⁺ (BB), [Al (H ₂ O) ₆] ³⁺ (BA), [Cu (H ₂ O) ₄] ²⁺ (CA), [Al (H ₂ O) ₅ ( OH)] ²⁺ (CB); H ₂ S (BA),\(\ce{NH2- (BB)}\), HS ⁻ (CB), NH ₃ (CA)

Q14.1.10

Identificar y etiquetar el ácido de Brønsted-Lowry, su base conjugada, la base de Brønsted-Lowry y su ácido conjugado en cada una de las siguientes ecuaciones:

1. \(\ce{NO2- + H2O ⟶ HNO2 + OH-}\)
2. \(\ce{HBr + H2O ⟶ H3O+ + Br-}\)
3. \(\ce{HS- + H2O ⟶ H2S + OH-}\)
4. \(\ce{H2PO4- + OH- ⟶HPO4^2- + H2O}\)
5. \(\ce{H2PO4- + HCl ⟶ H3PO4 + Cl-}\)
6. \(\ce{[Fe(H2O)5(OH)]^2+ + [Al(H2O)6]^3+ ⟶ [Fe(H2O)6]^3+ + [Al(H2O)5(OH)]^2+}\)
7. \(\ce{CH3OH + H- ⟶ CH3O- + H2}\)

Q14.1.11

¿Qué son las especies anfipróticas? Ilustrar con ecuaciones adecuadas.

S14.1.11

Las especies anfipróticas pueden ganar o perder un protón en una reacción química, actuando así como una base o un ácido. Un ejemplo es H ₂ O.

• Como un ácido:\(\ce{H2O}(aq) + \ce{NH3}(aq) \rightleftharpoons \ce{NH4+}(aq) + \ce{OH-}(aq)\).
• Como base:\(\ce{H2O}(aq) + \ce{HCl}(aq) \rightleftharpoons \ce{H3O+}(aq) + \ce{Cl-}(aq)\)

Q14.1.12

Indique cuáles de las siguientes especies son anfipróticas y escribir ecuaciones químicas que ilustran el carácter anfiprótico de estas especies:

1. H ₂ O
2. \(\ce{H2PO4-}\)
3. S ²⁻
4. \(\ce{CO3^2-}\)
5. \(\ce{HSO4-}\)

Q14.1.13

Indique cuáles de las siguientes especies son anfipróticas y escribir ecuaciones químicas que ilustren el carácter anfiprótico de estas especies.

1. NH ₃
2. \(\ce{HPO4-}\)
3. Br ⁻
4. \(\ce{NH4+}\)
5. \(\ce{ASO4^3-}\)

S14.113

anfiprótico:\(\ce{NH3 + H3O+ ⟶ NH4OH + H2O}\),\(\ce{NH3 + OCH3- ⟶ NH2- + CH3OH}\);\(\ce{HPO4^2- + OH- ⟶ PO4^3- + H2O}\),\(\ce{HPO4^2- + HClO4 ⟶ H2PO4- + ClO4-}\); no anfiprótico: Br ⁻;;\(\ce{NH4+}\);\(\ce{AsO4^3-}\)

Q14.1.14

¿La autoionización del agua es endotérmica o exotérmica? La constante de ionización para el agua (K _w) es\(2.9 \times 10^{-14}\) a 40 °C y\(9.6 \times 10^{-14}\) a 60 °C.

14.2: pH y pOH

Q14.2.1

Explique por qué una muestra de agua pura a 40 °C es neutra aunque [H ₃ O ⁺] = 1.7 × 10 ⁻⁷ M. K _w es 2.9 × 10 ⁻¹⁴ a 40 °C.

S14.2.1

En solución neutra [H ₃ O ⁺] = [OH ⁻]. A 40 °C,

[H ₃ O ⁺] = [OH ⁻] = (2.910 ⁻¹⁴) ^1/2 = 1.7 × 10 ⁻⁷.

Q14.2.2

La constante de ionización para el agua (K _w) es 2.9 × 10 ⁻¹⁴ a 40 °C. Calcular [H ₃ O ⁺], [OH ⁻], pH y pOH para agua pura a 40 °C.

Q14.2.3

La constante de ionización para el agua (K _w) es 9.614 × 10 ⁻¹⁴ a 60 °C. Calcular [H ₃ O ⁺], [OH ⁻], pH y pOH para agua pura a 60 °C.

S14.2.3

x = 3.101 × 10 ⁻⁷ M = [H ₃ O ⁺] = [OH ⁻]

pH = -log 3.101 × 10 ⁻⁷ = − (−6.5085) = 6.5085

PoH = pH = 6.5085

Q14.2.4

Calcular el pH y el PoH de cada una de las siguientes soluciones a 25 °C para lo cual las sustancias se ionizan completamente:

1. HCl 0.200 M
2. 0.0143 M NaOH
3. 3.0 M HNO ₃
4. 0.0031 M Ca (OH) ₂

Q14.2.5

Calcular el pH y el PoH de cada una de las siguientes soluciones a 25 °C para lo cual las sustancias se ionizan completamente:

1. 0.000259 M HClO ₄
2. NaOH 0.21 M
3. 0.000071 M Ba (OH) ₂
4. 2.5 M KOH

S14.2.5

pH = 3.587; pOH = 10.413; pH = 0.68; pOH = 13.32; pOH = 3.85; pH = 10.15; pH = −0.40; pOH = 14.4

Q14.2.6

¿Cuáles son el pH y el PoH de una solución de HCl 2.0 M, que se ioniza completamente?

Q14.2.6

¿Cuáles son las concentraciones de hidronio e hidróxido en una solución cuyo pH es 6.52?

S14.2.6

[H ₃ O ⁺] = 3.0 × 10 ⁻⁷ M; [OH ⁻] = 3.3 × 10 ⁻⁸ M

Q14.2.7

Calcular la concentración de iones hidrógeno y la concentración de iones hidróxido en el vino a partir de su pH. Consulte la figura a continuación para obtener información útil.

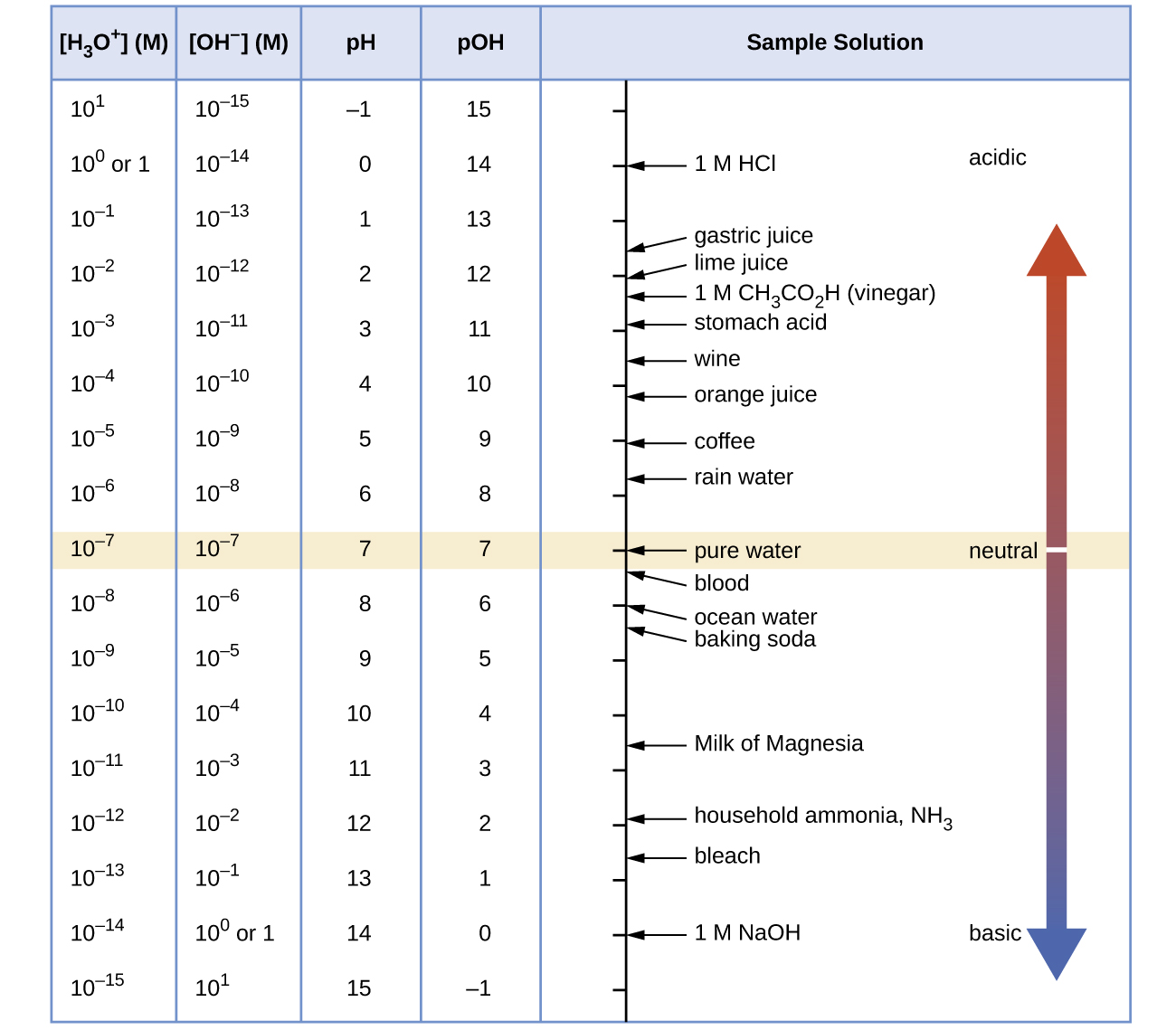
Q14.2.8

Calcular la concentración de iones hidronio y la concentración de iones hidróxido en jugo de lima a partir de su pH. Consulte la Figura para obtener información útil.

S14.2.9

[H ₃ O ⁺] = 1 × 10 ⁻² M; [OH ⁻] = 1 × 10 ⁻¹² M

Q14.2.9

Se encontró que la concentración de iones hidronio en una muestra de agua de lluvia es de 1.7 × 10 ⁻⁶ M a 25 °C. ¿Cuál es la concentración de iones hidróxido en el agua de lluvia?

Q14.2.10

La concentración de iones hidróxido en el amoníaco doméstico es de 3.2 × 10 ⁻³ M a 25 °C. ¿Cuál es la concentración de iones hidronio en la solución?

S14.2.10

[OH ⁻] = 3.1 × 10 ⁻¹² M

14.3: Fortalezas Relativas de Ácidos y Bases

Q14.3.1

Explique por qué la reacción de neutralización de un ácido fuerte y una base débil da una solución débilmente ácida.

Q14.3.2

Explique por qué la reacción de neutralización de un ácido débil y una base fuerte da una solución débilmente básica.

La sal se ioniza en solución, pero el anión reacciona ligeramente con el agua para formar el ácido débil. Esta reacción también forma OH ⁻, lo que hace que la solución sea básica.

Q14.3.3

Utilice esta lista de compuestos industriales importantes (y Figura) para responder las siguientes preguntas sobre: CaO, Ca (OH) ₂, CH ₃ CO ₂ H, CO _2, HCl, H ₂ CO ₃, HF, HNO ₂, HNO ₃, H ₃ PO ₄, H ₂ SO ₄, NH ₃, NaOH, Na ₂ CO ₃.

1. Identificar los ácidos fuertes de Brønsted-Lowry y las bases fuertes de Brønsted-Lowry.
2. Enumere aquellos compuestos en que pueden comportarse como ácidos de Brønsted-Lowry con fuerzas que se encuentran entre las de H ₃ O ⁺ y H ₂ O.
3. Enumerar aquellos compuestos en que pueden comportarse como bases de Brønsted-Lowry con fuerzas que se encuentran entre las de H ₂ O y OH ⁻.

Q14.3.4

El olor a vinagre se debe a la presencia de ácido acético, CH ₃ CO ₂ H, un ácido débil. Enumerar, en orden de concentración descendente, todas las especies iónicas y moleculares presentes en una solución acuosa 1- M de este ácido.

S14.3.4

[H ₂ O] > [CH ₃ CO ₂ H] >\(\ce{[H3O+]}\) ≈\(\ce{[CH3CO2- ]}\) > [OH ⁻]

Q14.3.5

El amoníaco doméstico es una solución de la base débil NH ₃ en agua. Enumerar, en orden de concentración descendente, todas las especies iónicas y moleculares presentes en una solución acuosa 1- M de esta base.

Q14.3.4

_{Explique por qué la constante de ionización, K a, para H 2 SO 4 es mayor que la constante de ionización para H 2 SO 3.}

S14.3.4

El estado de oxidación del azufre en H ₂ SO ₄ es mayor que el estado de oxidación del azufre en H ₂ SO ₃.

Q14.3.7

_{Explique por qué la constante de ionización, K a, para HI es mayor que la constante de ionización para HF.}

Q14.3.8

El jugo gástrico, el líquido digestivo producido en el estómago, contiene ácido clorhídrico, HCl. Leche de Magnesia, una suspensión de Mg (OH) ₂ sólido en un medio acuoso, a veces se usa para neutralizar el exceso de ácido estomacal. Escriba una ecuación equilibrada completa para la reacción de neutralización e identifique los pares ácido-base conjugados.

S14.3.8

\(\underset{\large\ce{BB}}{\ce{Mg(OH)2}(s)}+\underset{\large\ce{BA}}{\ce{HCl}(aq)}⟶\underset{\large\ce{CB}}{\ce{Mg^2+}(aq)}+\underset{\large\ce{CA}}{\ce{2Cl-}(aq)}+\underset{\:}{\ce{2H2O}(l)}\)

Q14.3.9

El ácido nítrico reacciona con óxido de cobre (II) insoluble para formar nitrato soluble de cobre (II), Cu (NO ₃) ₂, compuesto que se ha utilizado para prevenir el crecimiento de algas en piscinas. Escribir la ecuación química balanceada para la reacción de una solución acuosa de HNO ₃ con CuO.

Q14.3.10

Cuál es la constante de ionización a 25 °C para el ácido débil\(\ce{CH3NH3+}\), el ácido conjugado de la base débil CH ₃ NH ₂, K _b = 4.4 × 10 ⁻⁴.

S14.3.10

\(K_\ce{a}=2.3×10^{−11}\)

Q14.3.11

¿Cuál es la constante de ionización a 25 °C para el ácido débil\(\ce{(CH3)2NH2+}\), el ácido conjugado de la base débil (CH ₃) ₂ NH, K _b = 7.4 × 10 ⁻⁴?

Q14.3.12

¿Cuál base, CH ₃ NH ₂ o (CH ₃) ₂ NH, es la base más fuerte? ¿Qué ácido conjugado,\(\ce{(CH3)2NH2+}\) o (CH ₃) ₂ NH, es el ácido más fuerte?

S14.3.12

La base más fuerte o el ácido más fuerte es el que tiene el mayor K _b o K _a, respectivamente. En estos dos ejemplos, son (CH ₃) ₂ NH y\(\ce{CH3NH3+}\).

Q14.3.3

¿Cuál es el ácido más fuerte,\(\ce{NH4+}\) o HBro?

Q14.3.14

¿Cuál es la base más fuerte, (CH ₃) ₃ N o\(\ce{H2BO3-}\)?

S14.3.14

trietilamina.

Q14.3.15

Predice qué ácido en cada uno de los siguientes pares es el más fuerte y explica tu razonamiento para cada uno.

1. H ₂ O o HF
2. B (OH) ₃ o Al (OH) ₃
3. \(\ce{HSO3-}\)o\(\ce{HSO4-}\)
4. NH ₃ o H ₂ S
5. H ₂ O o H ₂ Te

Q14.3.16

Predecir qué compuesto en cada uno de los siguientes pares de compuestos es más ácido y explica tu razonamiento para cada uno.

1. \(\ce{HSO4-}\)o\(\ce{HSeO4-}\)
2. NH ₃ o H ₂ O
3. PH ₃ o HI
4. NH ₃ o PH ₃
5. H ₂ S o HBr

S14.3.16

1. \(\ce{HSO4-}\); mayor electronegatividad del ion central. H ₂ O;
2. NH ₃ es una base y el agua es neutra, o decidir sobre la base de valores de K _a. HOLA;
3. El pH ₃ es más débil que el HCl; el HCl es más débil que el HI. Así, PH ₃ es más débil que HI.
4. PH ₃; en compuestos binarios de hidrógeno con no metales, la acidez aumenta para el elemento más bajo en un grupo.
5. HBr; en un periodo, la acidez aumenta de izquierda a derecha; en un grupo, aumenta de arriba a abajo. Br está a la izquierda y por debajo de S, por lo que HBr es el ácido más fuerte.

Q14.3.17

Clasifique los compuestos en cada uno de los siguientes grupos en orden de aumento de acidez o basicidad, como se indica, y explique el orden que asigne.

1. acidez: HCl, HBr, HI
2. basicidad: H ₂ O, OH ⁻, H ⁻, Cl ⁻
3. basicidad: Mg (OH) ₂, Si (OH) ₄, ClO ₃ (OH) (Pista: La fórmula también podría escribirse como HClO ₄).
4. acidez: HF, H ₂ O, NH ₃, CH ₄

Q14.3.18

Clasifique los compuestos en cada uno de los siguientes grupos en orden de aumento de acidez o basicidad, como se indica, y explique el orden que asigne.

1. acidez: NaHSO ₃, NaHSEO ₃, NaHSO ₄
2. basicidad:\(\ce{BrO2-}\),\(\ce{ClO2-}\),\(\ce{IO2-}\)
3. acidez: HOCl, HOBr, HOI
4. acidez: HOCl, HocLo, HocLo ₂, HocLo ₃
5. basicidad:\(\ce{NH2-}\), HS ⁻, HTe ⁻,\(\ce{PH2-}\)
6. basicidad: BrO ⁻,\(\ce{BrO2-}\),\(\ce{BrO3-}\),\(\ce{BrO4-}\)

S14.3.18

1. NaHSEO ₃ < NaHSO ₃ < NaHSO ₄; en polioxiácidos, el elemento central más electronegativo, en este caso, forma el ácido más fuerte. El mayor número de átomos de oxígeno en el átomo central (dándole un estado de oxidación más alto) también crea una mayor liberación de átomos de hidrógeno, resultando en un ácido más fuerte. Como sal, la acidez aumenta de la misma manera.
2. \(\ce{ClO2- < BrO2- < IO2-}\); la basicidad de los aniones en una serie de ácidos será la opuesta a la acidez en sus oxiácidos. La acidez aumenta a medida que aumenta la electronegatividad del átomo central. Cl es más electronegativo que Br, y yo es el menos electronegativo de los tres.
3. HOI < HOBr < HOCl; en una serie de la misma forma de oxiácidos, la acidez aumenta a medida que aumenta la electronegatividad del átomo central. Cl es más electronegativo que Br, y yo es el menos electronegativo de los tres.
4. HOCl < HocLo < HocLo ₂ < HocLo ₃; en una serie de oxiácidos del mismo elemento central, la acidez aumenta a medida que aumenta el número de átomos de oxígeno (o a medida que aumenta el estado de oxidación del átomo central).
5. \(\ce{HTe- < HS- << PH2- < NH2-}\);\(\ce{PH2-}\) y\(\ce{NH2-}\) son aniones de bases débiles, por lo que actúan como bases fuertes hacia H ⁺. \(\ce{HTe-}\)y HS ⁻ son aniones de ácidos débiles, por lo que tienen un carácter menos básico. En un grupo periódico, cuanto más electronegativo tiene el anión más básico.
6. \(\ce{BrO4- < BrO3- < BrO2- < BrO-}\); con un mayor número de átomos de oxígeno (es decir, a medida que aumenta el estado de oxidación del ion central), el ácido correspondiente se vuelve más ácido y el anión en consecuencia menos básico.

Q14.3.19

Tanto el HF como el HCN se ionizan en agua de manera limitada. ¿Cuál de las bases conjugadas, F ⁻ o CN ⁻, es la base más fuerte? Ver Tabla.

Q14.3.20

El ingrediente activo formado por la aspirina en el cuerpo es el ácido salicílico, C ₆ H ₄ OH (CO ₂ H). El grupo carboxilo (−CO _2H) actúa como un ácido débil. El grupo fenol (un grupo OH unido a un anillo aromático) también actúa como un ácido pero un ácido mucho más débil. Enumerar, en orden de concentración descendente, todas las especies iónicas y moleculares presentes en una solución acuosa 0.001- M de C ₆ H ₄ OH (CO ₂ H).

\(\ce{[H2O] > [C6H4OH(CO2H)] > [H+]0 > [C6H4OH(CO2)- ] ≫ [C6H4O(CO2H)- ] > [OH- ]}\)

Qué representamos cuando escribimos:

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq)?\]

Q14.3.21

Explicar por qué los cálculos de equilibrio no son necesarios para determinar las concentraciones iónicas en soluciones de ciertos electrolitos fuertes como NaOH y HCl. ¿En qué condiciones son necesarios los cálculos de equilibrio como parte de la determinación de las concentraciones de todos los iones de algunos otros electrolitos fuertes en solución?

S14.3.21

Los electrolitos fuertes están 100% ionizados y, siempre y cuando los iones componentes no sean ácidos débiles ni bases débiles, las especies iónicas presentes resultan de la disociación del electrolito fuerte. Los cálculos de equilibrio son necesarios cuando uno (o más) de los iones es un ácido débil o una base débil.

Q14.3.22

¿Las concentraciones de ión hidronio e ion hidróxido en una solución de un ácido o una base en agua son directamente proporcionales o inversamente proporcionales? Explica tu respuesta.

Q14.3.23

¿Qué dos supuestos comunes pueden simplificar el cálculo de las concentraciones de equilibrio en una solución de un ácido débil?

S14.3.23

1. Supongamos que se puede descuidar el cambio en la concentración inicial del ácido a medida que se establece el equilibrio, por lo que esta concentración puede asumirse constante e igual al valor inicial de la concentración total de ácido.
2. Supongamos que podemos descuidar la contribución del agua a la concentración de equilibrio de H ₃ O ⁺.

Q14.3.24

¿Qué dos supuestos comunes pueden simplificar el cálculo de concentraciones de equilibrio en una solución de una base débil?

Q14.3.25

¿Cuál de las siguientes aumentará el porcentaje de NH ₃ que se convierte en el ion amonio en el agua (Pista: Use el principio de Lechâtelier.)?

1. adición de NaOH
2. adición de HCl
3. adición de NH ₄ Cl

S14.3.25

La adición de HCl

Q14.3.26

¿Cuál de los siguientes incrementará el porcentaje de HF que se convierte en el ion fluoruro en el agua?

1. adición de NaOH
2. adición de HCl
3. adición de NaF

Q14.3.27

¿Cuál es el efecto sobre las concentraciones de\(\ce{NO2-}\) HNO ₂ y OH ⁻ cuando se añaden lo siguiente a una solución de KNO ₂ en agua:

1. HCl
2. HNO ₂
3. NaOH
4. NaCl
5. KNO

La ecuación para el equilibrio es:

\[\ce{NO2-}(aq)+\ce{H2O}(l)⇌\ce{HNO2}(aq)+\ce{OH-}(aq)\]

S14.3.27

1. Al agregar HCl se agregarán iones H ₃ O ⁺, que luego reaccionarán con los iones OH ⁻, bajando su concentración. El equilibrio se desplazará hacia la derecha, aumentando la concentración de HNO ₂, y disminuyendo la concentración de\(\ce{NO2-}\) iones.
2. Agregar HNO ₂ aumenta la concentración de HNO ₂ y desplaza el equilibrio hacia la izquierda, aumentando la concentración de\(\ce{NO2-}\) iones y disminuyendo la concentración de iones OH ⁻.
3. Al agregar NaOH se agregan iones OH ⁻, que desplaza el equilibrio hacia la izquierda, aumentando la concentración de\(\ce{NO2-}\) iones y disminuyendo las concentraciones de HNO ₂.
4. La adición de NaCl no tiene efecto sobre las concentraciones de los iones.
5. Agregar KNO ₂ agrega\(\ce{NO2-}\) iones y desplaza el equilibrio hacia la derecha, aumentando las concentraciones de iones HNO ₂ y OH ⁻.

Q14.3.28

¿Cuál es el efecto en la concentración de ácido fluorhídrico, ión hidronio e ion fluoruro cuando se agregan los siguientes para separar soluciones de ácido fluorhídrico?

1. HCl
2. KF
3. NaCl
4. KOH
5. HF

La ecuación para el equilibrio es:

\[\ce{HF}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{F-}(aq)\]

Q14.3.29

¿Por qué la concentración de iones hidronio en una solución que es 0.10 M en HCl y 0.10 M en HCOOH se determina por la concentración de HCl?

S14.3.29

Este es un caso en el que la solución contiene una mezcla de ácidos de diferentes fuerzas de ionización. En solución, el HCO ₂ H existe principalmente como moléculas de HCO ₂ H debido a que la ionización del ácido débil es suprimida por el ácido fuerte. Por lo tanto, el HCO ₂ H aporta una cantidad insignificante de iones hidronio a la solución. El ácido más fuerte, el HCl, es el productor dominante de iones hidronio porque está completamente ionizado. En tal solución, el ácido más fuerte determina la concentración de iones hidronio, y la ionización del ácido más débil es fijada por el [H ₃ O ⁺] producido por el ácido más fuerte.

Q14.3.30

A partir de las concentraciones de equilibrio dadas, se calcula K _a para cada uno de los ácidos débiles y K _b para cada una de las bases débiles.

CH ₃ CO ₂ H:\(\ce{[H3O+]}\) = 1.34 × 10 ⁻³ M;

\(\ce{[CH3CO2- ]}\)= 1.34 × 10 ⁻³ M;

[CH ₃ CO ₂ H] = 9.866 × 10 ⁻² M;

ClO ⁻: [OH ⁻] = 4.0 × 10 ⁻⁴ M;

[HClO] = 2.38 × 10 ⁻⁵ M;

[ClO ⁻] = 0.273 M;

HCO ₂ H: [HCO ₂ H] = 0.524 M;

\(\ce{[H3O+]}\)= 9.8 × 10 ⁻³ M;\(\ce{[HCO2- ]}\) = 9.8 × 10 ⁻³ M;

\(\ce{C6H5NH3+ : [C6H5NH3+]}\)= 0.233 M;

[C ₆ H ₅ NH ₂] = 2.3 × 10 ⁻³ M;

\(\ce{[H3O+]}\)= 2.3 × 10 ⁻³ M

A partir de las concentraciones de equilibrio dadas, se calcula K _a para cada uno de los ácidos débiles y K _b para cada una de las bases débiles.

NH ₃: [OH ⁻] = 3.1 × 10 ⁻³ M;

\(\ce{[NH4+]}\)= 3.1 × 10 ⁻³ M;

[NH ₃] = 0.533 M;

HNO ₂:\(\ce{[H3O+]}\) = 0.011 M;

\(\ce{[NO2- ]}\)= 0.0438 M;

[HNO ₂] = 1.07 M;

(CH ₃) ₃ N: [(CH ₃) ₃ N] = 0.25 M;

[(CH ₃) ₃ NH ⁺] = 4.3 × 10 ⁻³ M;

[OH ⁻] = 4.3 × 10 ⁻³ M;

\(\ce{NH4+ : [NH4+]}\)= 0.100 M;

[NH ₃] = 7.5 × 10 ⁻⁶ M;

[H ₃ O ⁺] = 7.5 × 10 ⁻⁶ M

1. \(K_\ce{b}=1.8×10^{−5};\)
2. \(K_\ce{a}=4.5×10^{−4};\)
3. \(K_\ce{b}=7.4×10^{−5};\)
4. \(K_\ce{a}=5.6×10^{−10}\)

Q14.3.31

Determinar K _b para el ion nitrito,\(\ce{NO2-}\). En una solución 0.10- M esta base es 0.0015% ionizada.

Q14.3.32

Determinar K _a para el ion sulfato de hidrógeno,\(\ce{HSO4-}\). En una solución 0.10- M el ácido es 29% ionizado.

S14.3.32

\(K_\ce{a}=1.2×10^{−2}\)

Q14.3.33

Calcular la constante de ionización para cada uno de los siguientes ácidos o bases a partir de la constante de ionización de su base conjugada o ácido conjugado:

1. F ⁻
2. \(\ce{NH4+}\)
3. \(\ce{AsO4^3-}\)
4. \(\ce{(CH3)2NH2+}\)
5. \(\ce{NO2-}\)
6. \(\ce{HC2O4-}\)(como base)

Q14.3.52

Calcular la constante de ionización para cada uno de los siguientes ácidos o bases a partir de la constante de ionización de su base conjugada o ácido conjugado:

1. HTe ⁻ (como base)
2. \(\ce{(CH3)3NH+}\)
3. \(\ce{HAsO4^3-}\)(como base)
4. \(\ce{HO2-}\)(como base)
5. \(\ce{C6H5NH3+}\)
6. \(\ce{HSO3-}\)(como base)

S14.3.52

1. \(K_\ce{b}=4.3×10^{−12};\)
2. \(K_\ce{a}=1.4×10^{−10};\)
3. \(K_\ce{b}=1×10^{−7};\)
4. \(K_\ce{b}=4.2×10^{−3};\)
5. \(K_\ce{b}=4.2×10^{−3};\)
6. \(K_\ce{b}=8.3×10^{−13}\)

Q14.3.53

¿Para cuál de las siguientes soluciones debemos considerar la ionización del agua al calcular el pH o PoH?

1. 3 × 10 ⁻⁸ M HNO ₃
2. 0.10 g de HCl en 1.0 L de solución
3. 0.00080 g NaOH en 0.50 L de solución
4. 1 × 10 ⁻⁷ M Ca (OH) ₂
5. 0.0245 M KNO ₃

Q14.3.54

A pesar de que tanto NH ₃ como C ₆ H ₅ NH ₂ son bases débiles, NH ₃ es un ácido mucho más fuerte que C ₆ H ₅ NH ₂. ¿Cuál de las siguientes es correcta en equilibrio para una solución que inicialmente es 0.10 M en NH ₃ y 0.10 M en C ₆ H ₅ NH ₂?

1. \(\ce{[OH- ]}=\ce{[NH4+]}\)
2. \(\ce{[NH4+]}=\ce{[C6H5NH3+]}\)
3. \(\ce{[OH- ]}=\ce{[C6H5NH3+]}\)
4. [NH ₃] = [C ₆ H ₅ NH ₂]
5. tanto a como b son correctos

es la declaración correcta.

Q14.3.55

Calcular la concentración de equilibrio de los ácidos no ionizados y todos los iones en una solución que es 0.25 M en HCO ₂ H y 0.10 M en HClO.

Q14.3.56

Calcular la concentración de equilibrio de los ácidos no ionizados y todos los iones en una solución que es 0.134 M en HNO ₂ y 0.120 M en HBrO.

S14.3.56

[H ₃ O ⁺] = 7.5 × 10 ⁻³ M

[HNO ₂] = 0.126 [OH ⁻] = 1.3 × 10 ⁻¹² M [BrO ⁻] = 3.2 × 10 ⁻⁸ M [HBrO] = 0.120 M

Q14.3.57

Calcular la concentración de equilibrio de las bases no ionizadas y todos los iones en una solución que es 0.25 M en CH ₃ NH ₂ y 0.10 M en C ₅ H ₅ N (K _b = 1.7 × 10 ⁻⁹).

Q14.3.58

Calcular la concentración de equilibrio de las bases no ionizadas y todos los iones en una solución que es 0.115 M en NH ₃ y 0.100 M en C ₆ H ₅ NH ₂.

S14.3.58

[OH ⁻] =\(\ce{[NO4+]}\) = 0.0014 M

[NH ₃] = 0.144 M [H ₃ O ⁺] = 6.9 × 10 ⁻¹² M\(\ce{[C6H5NH3+]}\) = 3.9 × 10 ⁻⁸ M [C ₆ H ₅ NH ₂] = 0.100 M

Q14.3.59

Usando los valores K _a en el Apéndice H, coloque\(\ce{Al(H2O)6^3+}\) en la ubicación correcta en la Figura.

Q14.3.60

Calcular la concentración de todas las especies de solutos en cada una de las siguientes soluciones de ácidos o bases. Supongamos que se puede descuidar la ionización del agua, y mostrar que se puede descuidar el cambio en las concentraciones iniciales. Las constantes de ionización se pueden encontrar en el Apéndice H y el Apéndice I.

1. 0.0092 M HClO, un ácido débil
2. 0.0784 M C ₆ H ₅ NH ₂, una base débil
3. HCN 0.0810 M, un ácido débil
4. 0.11 M (CH ₃) ₃ N, una base débil
5. 0.120 M\(\ce{Fe(H2O)6^2+}\) un ácido débil, K _a = 1.6 × 10 ⁻⁷

S14.3.60

\(\ce{\dfrac{[H3O+][ClO- ]}{[HClO]}}=\dfrac{(x)(x)}{(0.0092−x)}≈\dfrac{(x)(x)}{0.0092}=3.5×10^{−8}\)

Resolviendo para x da 1.79 × 10 ⁻⁵ M. Este valor es menor al 5% de 0.0092, por lo que es válido el supuesto de que se pueda descuidar. Así, las concentraciones de especies de solutos en equilibrio son:

[H ₃ O ⁺] = [ClO] = 1.8 × 10 ⁻⁵ M [HClO] = 0.00092 M [OH ⁻] = 5.6 × 10 ⁻¹⁰ M;

\(\ce{\dfrac{[C6H5NH3+][OH- ]}{[C6H5NH2]}}=\dfrac{(x)(x)}{(0.0784−x)}≈\dfrac{(x)(x)}{0.0784}=4.6×10^{−10}\)

Resolviendo para x da 6.01 × 10 ⁻⁶ M.

Este valor es menor al 5% de 0.0784, por lo que es válido el supuesto de que se pueda descuidar. Así, las concentraciones de especies de soluto en equilibrio son:\(\ce{[CH3CO2- ]}\) = [OH ⁻] = 6.0 × 10 ⁻⁶ M [C ₆ H ₅ NH ₂] = 0.00784 [H ₃ O ⁺] = 1.7× 10 ⁻⁹ M;\(\ce{\dfrac{[H3O+][CN- ]}{[HCN]}}=\dfrac{(x)(x)}{(0.0810−x)}≈\dfrac{(x)(x)}{0.0810}=4×10^{−10}\) Resolviendo para x da 5.69 × 10 ⁻⁶ M. Este valor es menor al 5% de 0.0810, por lo que es válido el supuesto de que se pueda descuidar. Así, las concentraciones de especies de soluto en equilibrio son: [H ₃ O ⁺] = [CN ⁻] = 5.7 × 10 ⁻⁶ M [HCN] = 0.0810 M [OH ⁻] = 1.8 × 10 ⁻⁹ M;\(\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}}=\dfrac{(x)(x)}{(0.11−x)}≈\dfrac{(x)(x)}{0.11}=7.4×10^{−5}\) Resolviendo para x da 2.85 × 10 ⁻³ M. Este valor es menor al 5% de 0.11, por lo que es válido el supuesto de que se pueda descuidar. Así, las concentraciones de especies de soluto en equilibrio son: [(CH ₃) ₃ NH ⁺] = [OH ⁻] = 2.9 × 10 ⁻³ M [(CH ₃) ₃ N] = 0.11 M [H ₃ O ⁺] = 3.5 × 10 ⁻¹² M;\(\ce{\dfrac{[Fe(H2O)5(OH)+][H3O+]}{[Fe(H2O)6^2+]}}=\dfrac{(x)(x)}{(0.120−x)}≈\dfrac{(x)(x)}{0.120}=1.6×10^{−7}\) Resolviendo para x da 1.39 × 10 ⁻⁴ M. Este valor es menor al 5% de 0.120, por lo que es válido el supuesto de que se pueda descuidar. Así, las concentraciones de especies de soluto en equilibrio son: [Fe (H ₂ O) ₅ (OH) ⁺] = [H ₃ O ⁺] = 1.4 × 10 ⁻⁴ M\(\ce{[Fe(H2O)6^2+]}\) = 0.120 M [OH ⁻] = 7.2 × 10 ⁻¹¹ M

Q14.3.61

El ácido propiónico, C ₂ H ₅ CO ₂ H (K _a = 1.34 × 10 ⁻⁵), se utiliza en la fabricación de propionato de calcio, un conservante de alimentos. ¿Cuál es la concentración de iones hidronio en una solución 0.698- M de C ₂ H ₅ CO ₂ H?

Q14.3.62

El vinagre blanco es una solución al 5.0% en masa de ácido acético en agua. Si la densidad del vinagre blanco es de 1.007 g/cm ³, ¿cuál es el pH?

S14.3.62

pH = 2.41

Q14.3.63

La constante de ionización del ácido láctico, CH ₃ CH (OH) CO ₂ H, ácido que se encuentra en la sangre después del ejercicio extenuante, es de 1.36 × 10 ⁻⁴. Si se utilizan 20.0 g de ácido láctico para elaborar una solución con un volumen de 1.00 L, ¿cuál es la concentración de ión hidronio en la solución?

Q14.3.64

La nicotina, C ₁₀ H ₁₄ N ₂, es una base que aceptará dos protones (K ₁ = 7 × 10 ⁻⁷, K ₂ = 1.4 × 10 ⁻¹¹). ¿Cuál es la concentración de cada especie presente en una solución 0.050- M de nicotina?

S14.3.64

[C ₁₀ H ₁₄ N ₂] = 0.049 M

[C ₁₀ H ₁₄ N ₂ H ⁺] = 1.9 × 10 ⁻⁴ M\(\ce{[C10H14N2H2^2+]}\) = 1.4 × 10 ⁻¹¹ M [OH ⁻] = 1.9 × 10 ⁻⁴ M [H ₃ O ⁺] = 5.3 × 10 ⁻¹¹ M

Q14.3.65

El pH de una solución 0.20- M de HF es 1.92. Determine K _a para HF a partir de estos datos.

Q14.3.66

El pH de una solución 0.15- M de\(\ce{HSO4-}\) es 1.43. Determine K _a para\(\ce{HSO4-}\) a partir de estos datos.

S14.3.66

\(K_\ce{a}=1.2×10^{−2}\)

Q14.3.67

El pH de una solución 0.10- M de cafeína es 11.16. Determine K _b para cafeína a partir de estos datos:

\(\ce{C8H10N4O2}(aq)+\ce{H2O}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq)\)

Q14.3.68

El pH de una solución de amoníaco doméstico, una solución de 0.950 M de NH _3, es 11.612. Determinar K _b para NH ₃ a partir de estos datos.

S14.3.68

\(K_\ce{b}=1.77×10^{−5}\)

14.4: Hidrólisis de Soluciones Salinas

Q14.4.1

Determinar si las soluciones acuosas de las siguientes sales son ácidas, básicas o neutras:

1. Al (NO ₃) ₃
2. RBi
3. KHCO ₂
4. CH ₃ NH ₃ Br

Q14.4.2

Determinar si las soluciones acuosas de las siguientes sales son ácidas, básicas o neutras:

1. FeCl ₃
2. K ₂ CO ₃
3. NH ₄ Br
4. KClO ₄

S14.4.2

ácido; básico; ácido; neutro

Q14.4.3

La novocaína, C ₁₃ H ₂₁ O _{2 N 2} Cl, es la sal de la base procaína y ácido clorhídrico. La constante de ionización para la procaína es de 7 × 10 ⁻⁶. ¿Una solución de novocaína es ácida o básica? Cuáles son [H ₃ O ⁺], [OH ⁻], y pH de una solución 2.0% en masa de novocaína, suponiendo que la densidad de la solución es de 1.0 g/mL.

14.5: Ácidos polipróticos

Q15.5.1

¿Cuál de las siguientes concentraciones sería prácticamente igual en un cálculo de las concentraciones de equilibrio en una solución 0.134- M de H ₂ CO ₃, un ácido diprótico:

• \(\ce{[H3O+]}\),
• \([OH^−]\)
• \([H_2CO_3]\)
• \(\ce{[HCO3- ]}\)
• \(\ce{[CO3^2- ]}\)

No se necesitan cálculos para responder a esta pregunta.

S15.5.1

[H ₃ O ⁺] y\(\ce{[HCO3- ]}\) son iguales, H ₃ O ⁺ y\(\ce{HCO3-}\) son prácticamente iguales

Q15.5.2

Calcular la concentración de cada especie presente en una solución 0.050- M de H ₂ S.

Q15.5.3

Calcular la concentración de cada especie presente en una solución 0.010- M de ácido ftálico, C ₆ H ₄ (CO ₂ H) ₂.

S15.5.3

\(\ce{C6H4(CO2H)2}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{C6H4(CO2H)(CO2)-}(aq) \hspace{20px} K_\ce{a}=1.1×10^{−3}\)

\(\ce{C6H4(CO2H)(CO2)}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{C6H4(CO2)2^2-}(aq) \hspace{20px} K_\ce{a}=3.9×10^{−6}\)

[C ₆ H ₄ (CO ₂ H) ₂] 7.2 × 10 ⁻³ M, [C ₆ H ₄ (CO ₂ H) (CO ₂) ⁻] = [H ₃ O ⁺] 2.8 × 10 ⁻³ M,\(\ce{[C6H4(CO2)2^2- ]}\) 3.9 × 10 ⁻⁶ M, [OH ⁻] 3.6 × 10 ⁻¹² M

Q15.5.4

El ácido salicílico, HOC ₆ H ₄ CO ₂ H, y sus derivados han sido utilizados como analgésicos desde hace mucho tiempo. El ácido salicílico se presenta en pequeñas cantidades en las hojas, corteza y raíces de alguna vegetación (más notablemente históricamente en la corteza del sauce). Los extractos de estas plantas se han utilizado como medicamentos durante siglos. El ácido se aisló por primera vez en el laboratorio en 1838.

1. Ambos grupos funcionales del ácido salicílico se ionizan en agua, con K _a = 1.0 × 10 ⁻³ para el grupo —CO ₂ H y 4.2 × 10 ⁻¹³ para el grupo −OH. Cuál es el pH de una solución saturada del ácido (solubilidad = 1.8 g/L).
2. La aspirina fue descubierta como resultado de los esfuerzos para producir un derivado del ácido salicílico que no sería irritante para el revestimiento del estómago. La aspirina es ácido acetilsalicílico, CH ₃ CO ₂ C ₆ H ₄ CO ₂ H. El grupo funcional −CO ₂ H aún está presente, pero su acidez es reducida, K _a = 3.0 × 10 ⁻⁴. Cuál es el pH de una solución de aspirina con la misma concentración que una solución saturada de ácido salicílico (Ver Parte a).
3. Bajo algunas condiciones, la aspirina reacciona con el agua y forma una solución de ácido salicílico y ácido acético:

\[\ce{CH3CO2C6H4CO2H}(aq)+\ce{H2O}(l)⟶\ce{HOC6H4CO2H}(aq)+\ce{CH3CO2H}(aq)\]

1. ¿Cuál de los ácidos ácido salicílico o ácido acético produce más iones hidronio en solución tal solución?
2. ¿Cuáles son las concentraciones de moléculas e iones en una solución producida por la hidrólisis de 0.50 g de aspirina disueltos en agua suficiente para dar 75 mL de solución?

Q15.5.5

El ion hTe ⁻ es una especie anfiprótica; puede actuar como un ácido o una base.

1. ¿Qué es K _a para la reacción ácida de HTe ⁻ con H ₂ O?
2. ¿Qué es K _b para la reacción en la que HTe ⁻ funciona como base en el agua?
3. Demostrar si se puede descuidar o no la segunda ionización de H ₂ Te en el cálculo de [hTe ⁻] en una solución 0.10 M de H ₂ Te.

S15.5.5

1. \(K_{\ce a2}=1×10^{−5};\)
2. \(K_\ce{b}=4.3×10^{−12};\)
3. \(\ce{\dfrac{[Te^2- ][H3O+]}{[HTe- ]}}=\dfrac{(x)(0.0141+x)}{(0.0141−x)}≈\dfrac{(x)(0.0141)}{0.0141}=1×10^{−5}\). Resolviendo para x da 1 × 10 ⁻⁵ M. Por lo tanto, en comparación con 0.014 M, este valor es despreciable (0.071%).

14.6: Búferes

Q14.6.1

Explique por qué se puede preparar un tampón a partir de una mezcla de NH ₄ Cl y NaOH pero no de NH ₃ y NaOH.

Q14.6.2

Explique por qué el pH no cambia significativamente cuando se agrega una pequeña cantidad de un ácido o una base a una solución que contiene cantidades iguales del ácido H ₃ PO ₄ y una sal de su base conjugada NaH ₂ PO ₄.

S14.6.2

El exceso de H ₃ O ⁺ se elimina principalmente por la reacción:

\(\ce{H3O+}(aq)+\ce{H2PO4-}(aq)⟶\ce{H3PO4}(aq)+\ce{H2O}(l)\)El exceso de base se elimina mediante la reacción:\(\ce{OH-}(aq)+\ce{H3PO4}(aq)⟶\ce{H2PO4-}(aq)+\ce{H2O}(l)\)

Q14.6.3

Explique por qué el pH no cambia significativamente cuando se agrega una pequeña cantidad de un ácido o una base a una solución que contiene cantidades iguales de la base NH ₃ y una sal de su conjugado ácido NH ₄ Cl.

Q14.6.4

¿Qué es [H ₃ O ⁺] en una solución de 0.25 M CH ₃ CO ₂ H y 0.030 M nACh ₃ CO ₂?

\(\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−5}\)

S14.6.4

[H ₃ O ⁺] = 1.5 × 10 ⁻⁴ M

Q14.6.5

¿Qué es [H ₃ O ⁺] en una solución de 0.075 M HNO ₂ y 0.030 M NaNO ₂?

S14.6.6

\(\ce{HNO2}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) \hspace{20px} K_\ce{a}=4.5×10^{−5}\)

Q14.6.6

¿Qué es [OH ⁻] en una solución de 0.125 M CH ₃ NH ₂ y 0.130 M CH ₃ NH ₃ Cl?

S14.6.6

\(\ce{CH3NH2}(aq)+\ce{H2O}(l)⇌\ce{CH3NH3+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=4.4×10^{−4}\)

[OH ⁻] = 4.2 × 10 ⁻⁴ M

Q14.6.7

¿Qué es [OH ⁻] en una solución de 1.25 M NH ₃ y 0.78 M NH ₄ NO ₃?

S14.6.7

\(\ce{NH3}(aq)+\ce{H2O}(l)⇌\ce{NH4+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=1.8×10^{−5}\)

Q14.6.8

¿Qué concentración de NH ₄ NO ₃ se requiere para hacer [OH ⁻] = 1.0 × 10 ⁻⁵ en una solución 0.200- M de NH ₃?

S14.6.8

[NH ₄ NO ₃] = 0.36 M

Q14.6.9A

¿Qué concentración de NaF se requiere para hacer [H ₃ O ⁺] = 2.3 × 10 ⁻⁴ en una solución 0.300- M de HF?

Q14.6.9B

Cuál es el efecto sobre la concentración de ácido acético, ión hidronio e ion acetato cuando se agregan los siguientes a una solución tampón ácida de concentraciones iguales de ácido acético y acetato de sodio:

1. HCl
2. KCH ₃ CO ₂
3. NaCl
4. KOH
5. CH ₃ CO ₂ H

S14.6.10

1. El HCl agregado incrementará ligeramente la concentración de H ₃ O ⁺, lo que reaccionará\(\ce{CH3CO2-}\) y producirá CH ₃ CO ₂ H en el proceso. Así,\(\ce{[CH3CO2- ]}\) disminuye y [CH ₃ CO ₂ H] aumenta.
2. El KCH ₃ CO ₂ agregado aumentará la concentración de la\(\ce{[CH3CO2- ]}\) cual reaccionará con H ₃ O ⁺ y producirá CH ₃ CO ₂ H en el proceso. Así, [H ₃ O ⁺] disminuye ligeramente y [CH ₃ CO ₂ H] aumenta.
3. El NaCl agregado no tendrá ningún efecto sobre la concentración de los iones.
4. El KOH agregado producirá iones OH ⁻, los cuales reaccionarán con el H ₃ O ⁺, reduciendo así [H ₃ O ⁺]. Algunos CH ₃ CO ₂ H adicionales se disociarán, produciendo\(\ce{[CH3CO2- ]}\) iones en el proceso. Así, [CH ₃ CO ₂ H] disminuye ligeramente y\(\ce{[CH3CO2- ]}\) aumenta.
5. El CH ₃ CO ₂ H agregado incrementará su concentración, provocando que más de él se disocie y produzca más\(\ce{[CH3CO2- ]}\) y H ₃ O ⁺ en el proceso. Así, [H ₃ O ⁺] aumenta ligeramente y\(\ce{[CH3CO2- ]}\) aumenta.

Q14.6.11

Cuál es el efecto sobre la concentración de amoníaco, ión hidróxido e ión amonio cuando se agregan los siguientes a una solución tampón básica de concentraciones iguales de amoníaco y nitrato de amonio:

1. KI
2. NH ₃
3. HOLA
4. NaOH
5. NH ₄ Cl

¿Cuál será el pH de una solución tampón preparada a partir de 0.20 mol NH ₃, 0.40 mol NH ₄ NO ₃, y solo agua suficiente para dar 1.00 L de solución?

pH = 8.95

Calcular el pH de una solución tampón preparada a partir de 0.155 mol de ácido fosfórico, 0.250 mol de KH ₂ PO ₄, y suficiente agua para hacer 0.500 L de solución.

¿Cuánto sólido NACh ₃ CO ₂ •3H ₂ O debe agregarse a 0.300 L de una solución de ácido acético 0.50- M para dar un tampón con un pH de 5.00? (Pista: Suponga un cambio insignificante en el volumen a medida que se agrega el sólido).

37 g (0.27 mol)

¿Qué masa de NH ₄ Cl se debe agregar a 0.750 L de una solución 0.100- M de NH ₃ para dar una solución tampón con un pH de 9.26? (Pista: Suponga un cambio insignificante en el volumen a medida que se agrega el sólido).

Q14.6.1

Se prepara una solución tampón a partir de volúmenes iguales de ácido acético 0.200 M y acetato de sodio 0.600 M. Use 1.80 × 10 ⁻⁵ como K _a para ácido acético.

1. ¿Cuál es el pH de la solución?
2. ¿La solución es ácida o básica?

Q14.6.1

¿Cuál es el pH de una solución que resulta cuando se agregan 3.00 mL de HCl 0.034 M a 0.200 L del tampón original?

1. pH = 5.222;
2. La solución es ácida. (c) pH = 5.221

Q14.6.1

Se añadió una muestra de 5.36 g de NH ₄ Cl a 25.0 mL de NaOH 1.00 M y la solución resultante se diluyó a 0.100 L.

1. ¿Cuál es el pH de esta solución tampón?
2. ¿La solución es ácida o básica?
3. ¿Cuál es el pH de una solución que resulta cuando se agregan 3.00 mL de HCl 0.034 M a la solución?

¿Qué ácido en [link] es el más apropiado para la preparación de una solución tampón con un pH de 3.1? Explica tu elección.

Para preparar el mejor tampón para un AH ácido débil y su sal, la relación\(\dfrac{\ce{[H3O+]}}{K_\ce{a}}\) debe ser lo más cercana posible a 1 para una acción efectiva del tampón. La concentración de [H ₃ O ⁺] en un tampón de pH 3.1 es [H ₃ O ⁺] = 10 ^−3.1 = 7.94 × 10 ⁻⁴ M

Ahora podemos resolver para K _a del mejor ácido de la siguiente manera:

\(\dfrac{\ce{[H3O+]}}{K_\ce{a}}=1\)

\(K_\ce{a}=\dfrac{\ce{[H3O+]}}{1}=7.94×10^{−4}\)

En [link], el ácido con la K _a más cercana a 7.94 × 10 ⁻⁴ es HF, con _una K a de 7.2 × 10 ⁻⁴.

¿Qué ácido en [link] es el más apropiado para la preparación de una solución tampón con un pH de 3.7? Explica tu elección.

¿Qué base en [link] es la más adecuada para la preparación de una solución tampón con un pH de 10.65? Explica tu elección.

Para tampones con pH > 7, se debe usar una base débil y su sal. El búfer más efectivo tendrá una relación\(\dfrac{\ce{[OH- ]}}{K_\ce{b}}\) que sea lo más cercana posible a 1. El PoH del búfer es 14.00 − 10.65 = 3.35. Por lo tanto, [OH ⁻] es [OH ⁻] = 10 ^−PoH = 10 ^−3.35 = 4.467 × 10 ⁻⁴ M.

Ahora podemos resolver para K _b de la mejor base de la siguiente manera:\(\dfrac{\ce{[OH- ]}}{K_\ce{b}}=1\) K _b = [OH ⁻] = 4.47 × 10 ⁻⁴ En [link], la base con el K _b más cercano a 4.47 × 10 ⁻⁴ es CH ₃ NH ₂, con una K _b = 4.4 × 10 ⁻⁴.

¿Qué base en [link] es la más adecuada para la preparación de una solución tampón con un pH de 9.20? Explica tu elección.

Q14.6.4

_{La sacarina, C 7 H 4 NSO 3 H, es un ácido débil (K a = 2.1 × 10 ⁻²).} Si se prepararon 0.250 L de cola dietética con un pH tamponado de 5.48 a partir de 2.00 × 10 ⁻³ g de sacárido de sodio, Na (C ₇ H ₄ NSO ₃), ¿cuáles son las concentraciones finales de sacarina y sacárido de sodio en la solución?

S14.6.4

La masa molar del sacárido de sodio es 205.169 g/mol. Usando las abreviaturas HA para sacarina y NaA para sacárido de sodio, el número de moles de NaA en la solución es:

9.75 × 10 ⁻⁶ mol. Esto se ioniza inicialmente para formar iones sacarina, A ⁻, con: [A ⁻] = 3.9 × 10 ⁻⁵ M

Q14.6.5

Cuál es el pH de 1.000 L de una solución de 100.0 g de ácido glutámico (C ₅ H ₉ NO ₄, un ácido diprótico; K ₁ = 8.5 × 10 ⁻⁵, K ₂ = 3.39 × 10 ⁻¹⁰) al que se le ha añadido 20.0 g de NaOH durante el preparación de glutamato monosódico, el agente saborizante? ¿Cuál es el pH cuando se ha agregado exactamente 1 mol de NaOH por mol de ácido?

14.7: Titulación ácido-base

Q14.7.1

Explicar cómo elegir el indicador ácido-base apropiado para la titulación de una base débil con un ácido fuerte.

S14.7.1

En el punto de equivalencia en la titulación de una base débil con un ácido fuerte, la solución resultante es ligeramente ácida debido a la presencia del ácido conjugado. Así, elija un indicador que cambie de color en el rango ácido y entre paréntesis el pH en el punto de equivalencia. El naranja metílico es un buen ejemplo.

Q14.7.2

Explique por qué un indicador ácido-base cambia de color en un rango de valores de pH en lugar de a un pH específico.

Q14.7.3

Por qué podemos ignorar el aporte del agua a las concentraciones de H ₃ O ⁺ en las soluciones de los siguientes ácidos:

• 0.0092 M HClO, un ácido débil
• HCN 0.0810 M, un ácido débil
• 0.120 M\(\ce{Fe(H2O)6^2+}\) un ácido débil, K _a = 1.6 × 10 ⁻⁷

pero no el aporte del agua a la concentración de OH ⁻?

S14.7.3

En una solución ácida, la única fuente de iones OH ⁻ es el agua. Utilizamos K _w para calcular la concentración. Si se descuidara el aporte del agua, la concentración de OH ⁻ sería cero.

Q14.7.4

Podemos ignorar la contribución del agua a la concentración de OH ⁻ en una solución de las siguientes bases:

0.0784 M C ₆ H ₅ NH ₂, una base débil

0.11 M (CH ₃) ₃ N, una base débil

pero no el aporte del agua a la concentración de H ₃ O ⁺?

Q14.7.5

Dibujar una curva para una serie de soluciones de HF. Trazar [H ₃ O ⁺] _total en el eje vertical y la concentración total de HF (la suma de las concentraciones tanto de las moléculas de HF ionizadas como no ionizadas) en el eje horizontal. Dejar que la concentración total de HF varíe de 1 × ^{10 −10} M a 1 × 10 ⁻² M.

Q14.7.6

Dibujar una curva similar a la mostrada en la Figura para una serie de soluciones de NH ₃. Trazar [OH ⁻] en el eje vertical y la concentración total de NH ₃ (moléculas NH ₃ ionizadas y no ionizadas) en el eje horizontal. Dejar que la concentración total de NH ₃ varíe de 1 × ^{10 −10} M a 1 × 10 ⁻² M.

Q14.7.7

Calcular el pH en los siguientes puntos en una titulación de 40 mL (0.040 L) de ácido barbitúrico 0.100 M (K _a = 9.8 × 10 ⁻⁵) con KOH 0.100 M.

1. sin KOH agregado
2. Se añadieron 20 ml de solución de KOH
3. 39 mL de solución de KOH añadidos
4. Se añadieron 40 ml de solución de KOH
5. Se añadieron 41 ml de solución de KOH

S14.7.7

1. pH = 2.50;
2. pH = 4.01;
3. pH = 5.60;
4. pH = 8.35;
5. pH = 11.08

Q14.7.8

El dinitrofenol indicador es un ácido con _{una K a} de 1.1 × 10 ⁻⁴. En una solución de 1.0 × 10 ⁻⁴ - M, es incoloro en ácido y amarillo en base. Calcular el rango de pH sobre el cual va de 10% ionizado (incoloro) a 90% ionizado (amarillo).