17.4: La ecuación de Nernst
- Page ID
- 75239
- Relacionar los potenciales celulares con los cambios de energía libre
- Utilice la ecuación de Nernst para determinar los potenciales celulares en condiciones no estándar
- Realizar cálculos que impliquen la conversión entre potenciales celulares, cambios de energía libre y constantes de equilibrio
Ahora ampliaremos la electroquímica determinando la relación entre\(E^\circ_\ce{cell}\) y las cantidades termodinámicas como Δ G° (energía libre de Gibbs) y K (la constante de equilibrio). En las celdas galvánicas, la energía química se convierte en energía eléctrica, que puede hacer trabajo. El trabajo eléctrico es el producto de la carga transferida multiplicada por la diferencia de potencial (voltaje):
\[\mathrm{electrical\: work=volts \times (charge\: in\: coulombs)=J} \nonumber \]
La carga en 1 mol de electrones viene dada por la constante de Faraday (F)
\[ \begin{align*} F &=\dfrac{6.022 \times 10^{23}\:e^-}{mol} \times \dfrac{1.602 \times 10^{−19}\:C}{e^-} \\[4pt] &=9.648 \times 10^4\:\dfrac{C}{mol} \\[4pt] &=9.648 \times 10^4\:\dfrac{J}{V⋅mol} \end{align*} \nonumber \]
Por lo tanto
\[\mathrm{total\: charge=(number\: of\: moles\: of\: e^-)} \times F=nF \nonumber \]
En esta ecuación,\(n\) se encuentra el número de moles de electrones para la reacción equilibrada de oxidación-reducción. El potencial celular medido es el potencial máximo que puede producir la celda y está relacionado con el trabajo eléctrico (w ele) por
\[E_\ce{cell}=\dfrac{−w_\ce{ele}}{nF}\hspace{40px}\ce{or}\hspace{40px}w_\ce{ele}=−nFE_\ce{cell} \nonumber \]
El signo negativo para el trabajo indica que el trabajo eléctrico es realizado por el sistema (la celda galvánica) en los alrededores. En un capítulo anterior, la energía libre se definió como la energía que estaba disponible para hacer el trabajo. En particular, el cambio en la energía libre se definió en términos del trabajo máximo (\(w_{max}\)), que, para los sistemas electroquímicos, es\(w_{ele}\).
\[\begin{align*} ΔG&=w_\ce{max}=w_\ce{ele} \\[4pt] &=−nFE_\ce{cell} \end{align*} \nonumber \]
Podemos verificar que los signos son correctos cuando nos damos cuenta de que\(n\) y\(F\) son constantes positivas y que las células galvánicas, que tienen potenciales celulares positivos, implican reacciones espontáneas. Así, las reacciones espontáneas, que tienen\(ΔG < 0\), deben tener\(E_{cell} > 0\). Si todos los reactivos y productos están en sus estados estándar, esto se convierte en
\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]
Esto proporciona una manera de relacionar los potenciales celulares estándar con las constantes de equilibrio, ya que
\[ΔG°=−RT\ln K \nonumber \]
\[−nFE^\circ_\ce{cell}=−RT\ln K \nonumber \]
o
\[ E^\circ_\ce{cell}=\dfrac{RT}{nF}\ln K \nonumber \]
La mayoría de las veces, las reacciones electroquímicas se realizan a temperatura estándar (298.15 K). La recolección de términos a esta temperatura rinde
\[\begin{align*} E^\circ_\ce{cell}&=\dfrac{RT}{nF}\:\ln K \\[4pt] &=\dfrac{\left(8.314\:\dfrac{\ce{J}}{\textrm{K⋅mol}}\right)(298.15\:K)}{n \times 96,485\: \textrm{C/V⋅mol}}\:\ln K \\[4pt] &=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K \end{align*} \nonumber \]
donde\(n\) está el número de moles de electrones. El logaritmo en las ecuaciones que involucran potenciales celulares a menudo se expresa usando logaritmos de base 10 (es decir,\(\log_{10}\) o simplemente\(\log\)), que cambia la constante por un factor de 2.303:
\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]
Así, si Δ G°, K, o\(E^\circ_\ce{cell}\) se conoce o se puede calcular, las otras dos cantidades se pueden determinar fácilmente. Las relaciones se muestran gráficamente en la Figura\(\PageIndex{1}\).
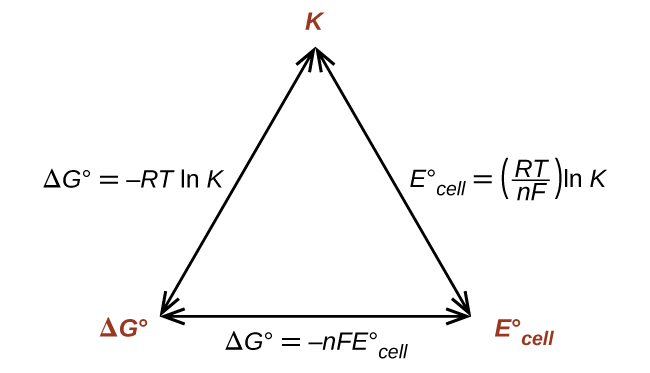
Dada cualquiera de las cantidades, se pueden calcular las otras dos.
¿Cuál es el cambio de energía libre estándar de Gibbs y la constante de equilibrio para la siguiente reacción a 25 °C?
\[\ce{2Ag+}(aq)+\ce{Fe}(s)⇌\ce{2Ag}(s)+\ce{Fe^2+}(aq) \nonumber \]
Así lution
La reacción implica una reacción de oxidación-reducción, por lo que el potencial celular estándar se puede calcular utilizando los datos de la Tabla P1.
\ [\ begin {alinear*}
&\ textrm {ánodo (oxidación):}\ ce {Fe} (s) ⟶\ ce {Fe^2+} (aq) +\ ce {2e-}\ hespacio {40px} E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {−0.447\: V}\ nonumber\\
&\ textrm {cátodo (reducción):} 2\ veces (\ ce {Ag+} (aq) +\ ce {e-} ⟶\ ce {Ag} (s))\ hspace {40px} E^\ circ_ {\ ce {Ag+/Ag}} =\ mathrm {0.7996\ : V}\ nonumber\\
&E^\ circ_\ ce {celda} =E^\ circ_\ ce {cátodo} −E^\ circ_\ ce {ánodo} =E^\ circ_ {\ ce {Ag+/Ag}} −E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {+1.247\: V}\ nonumber
\ end align{ *}\ nonumber\]
Recuerde que el potencial de celda para el cátodo no se multiplica por dos al determinar el potencial de celda estándar. Con n = 2, la constante de equilibrio es entonces
\[E^\circ_\ce{cell}=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \nonumber \]
\[\begin{align*} K&=10^{n \times E^\circ_\ce{cell}/\mathrm{0.0592\: V}} \\[4pt] &=10^{2 \times \mathrm{1.247\: V/0.0592\: V}} \\[4pt] &=10^{42.128} \\[4pt] &=1.3 \times 10^{42}\end{align*} \nonumber \]
La energía libre estándar es entonces
\[ΔG°=−nFE^\circ_\ce{cell} \nonumber \]
\[ΔG°=\mathrm{−2 \times 96,485\:\dfrac{J}{\textrm{V⋅mol}} \times 1.247\: V=−240.6\:\dfrac{kJ}{mol}} \nonumber \]
Comprueba tu respuesta: Un potencial celular estándar positivo significa una reacción espontánea, por lo que el cambio estándar de energía libre debe ser negativo, y una constante de equilibrio debe ser >1.
¿Cuál es el cambio estándar de energía libre de Gibbs y la constante de equilibrio para la siguiente reacción a temperatura ambiente? ¿La reacción es espontánea?
\[\ce{Sn}(s)+\ce{2Cu^2+}(aq)⇌\ce{Sn^2+}(aq)+\ce{2Cu+}(aq) \nonumber \]
- Contestar
-
Espontáneo; n = 2\(E^\circ_\ce{cell}=\mathrm{+0.291\: V}\);\(ΔG°=\mathrm{−56.2\:\dfrac{kJ}{mol}}\);;\(K = 6.8 \times 10^9\).
Ahora que se ha hecho la conexión entre la energía libre y los potenciales celulares, siguen concentraciones no estándar. Recordemos que
\[ΔG=ΔG°+RT\ln Q \nonumber \]
donde\(Q\) está el cociente de reacción (véase el capítulo sobre fundamentos de equilibrio). Conversión a potenciales celulares:
\[−nFE_\ce{cell}=−nFE^\circ_\ce{cell}+RT\ln Q \label{nernst1A} \]
o
\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \label{nernst1B} \]
La ecuación\ ref {Nernst1B} es la ecuación generalizada de Nernst que es aplicable a cualquier temperatura. Sin embargo, se puede simplificar para reacciones que ocurren a 25 °C (298.15 K) reescribiéndola como
\[E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0257\: V}}{n}\:\ln Q \label{nernst2A} \]
o
\[ E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\log_{10} Q \label{nernst2B} \]
Si la temperatura no es 298.15 K, es necesario recalcular el potencial con la Ecuación\ ref {Nernst1B}. Con la ecuación de Nernst, es posible calcular el potencial celular en condiciones no estándar. Este ajuste es necesario porque los potenciales determinados bajo diferentes condiciones tendrán diferentes valores.
Considere la siguiente reacción a temperatura ambiente:
\[\ce{Co}(s)+\ce{Fe^2+}(aq,\:1.94\:M)⟶\ce{Co^2+}(aq,\: 0.15\:M)+\ce{Fe}(s) \nonumber \]
¿El proceso es espontáneo?
Solución
Hay dos formas de resolver el problema. Si la información termodinámica en la Tabla T1 estuviera disponible, se podría calcular el cambio de energía libre. Si el cambio de energía libre es negativo, el proceso es espontáneo. El otro enfoque, que usaremos, requiere información como la que se da en la Tabla P1. Usando esos datos, se puede determinar el potencial celular. Si el potencial celular es positivo, el proceso es espontáneo. Recopilación de información de la Tabla P1 y el problema,
\ [\ begin {align*}
&\ textrm {Ánodo (oxidación):}\ ce {Co} (s) ⟶\ ce {Co^2+} (aq) +\ ce {2e-}\ hspace {40px} E^\ circ_ {\ ce {Co^2+/Co}} =\ mathrm {−0.28\: V}\\
&\ textrm {Cátodo (reducción):}\ ce {Fe^2+} (aq) +\ ce {2e-} ⟶\ ce {Fe} (s)\ hspace {40px} E^\ circ_ {\ ce {Fe^2+/Fe}} =\ mathrm {−0.447\: V}\\
&E^\ circ_\ ce {celda} =E^\ circ_\ ce {cátodo} −E^\ circ_\ ce {ánodo} =\ mathrm {−0.447\: V− (−0.28\: V) =−0.17\: V}
\ end {align*}\ nonumber\]
El proceso no es espontáneo bajo condiciones estándar. Utilizando la ecuación de Nernst y las concentraciones señaladas en el problema y\(n = 2\),
\[Q=\ce{\dfrac{[Co^2+]}{[Fe^2+]}}=\dfrac{0.15\:M}{1.94\:M}=0.077 \nonumber \]
Ahora podemos insertarlos en la Ecuación de Nernst a temperatura ambiente (Ecuación\ ref {Nernst2B})
\[\begin{align*} E_\ce{cell} &=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \\[4pt] &=\mathrm{−0.17\: V−\dfrac{0.0592\: V}{2}\:\log 0.077} \\[4pt] &=\mathrm{−0.17\: V+0.033\: V=−0.14\: V} \end{align*} \nonumber \]
El proceso es (todavía) no espontáneo.
¿Cuál es el potencial celular para la siguiente reacción a temperatura ambiente?
\[\ce{Al}(s)│\ce{Al^3+}(aq,\:0.15\:M)║\ce{Cu^2+}(aq,\:0.025\:M)│\ce{Cu}(s) \nonumber \]
¿Cuáles son los valores de n y Q para la reacción general? ¿La reacción es espontánea bajo estas condiciones?
- Contestar
-
n = 6; Q = 1440; Célula E = +1.97 V, espontánea.
Por último, vamos a echar un breve vistazo a un tipo especial de célula llamada célula de concentración. En una celda de concentración, los electrodos son del mismo material y las medias celdas difieren solo en concentración. Dado que uno o ambos compartimentos no es estándar, los potenciales celulares serán desiguales; por lo tanto, habrá una diferencia de potencial, que se puede determinar con la ayuda de la ecuación de Nernst.
¿Cuál es el potencial celular de la célula de concentración descrita por
\[\ce{Zn}(s)│\ce{Zn^2+}(aq,\: 0.10\:M)║\ce{Zn^2+}(aq,\: 0.50\:M)│\ce{Zn}(s) \nonumber \]
Así lution
De la información dada:
\ [\ begin {align*}
&\ textrm {Ánodo:}\ ce {Zn} (s) ⟶\ ce {Zn^2+} (aq,\: 0.10\ :M) +\ ce {2e-}\ hspace {40px} E^\ circ_\ ce {ánodo} =\ mathrm {−0.7618\: V}\\\
&\ textrm {cátodo:}\ ce {Zn^2+} (aq,\: 0.50\ :M) +\ ce {2e-} ⟶\ ce {Zn} (s)\ hspace {40px} E^\ circ_\ ce {cátodo} =\ mathrm {−0.7618\: V}\\
& amp;\ overline {\ textrm {General:}\ ce {Zn^2+} (aq,\: 0.50\ :M) ⟶\ ce {Zn^2+} (aq,\: 0.10\ :M)\ hspace {40px} E^\ circ_\ ce {cell} =\ mathrm {0.000\: V}}
\ end {align*}\ nonumber\]
El potencial de celda estándar es cero porque el ánodo y el cátodo implican la misma reacción; solo cambia la concentración de Zn 2 +. Sustituyendo en la ecuación de Nernst,
\[E_\ce{cell}=\mathrm{0.000\: V−\dfrac{0.0592\: V}{2}\:\log\dfrac{0.10}{0.50}=+0.021\: V} \nonumber \]
y el proceso es espontáneo en estas condiciones.
Consulta tu respuesta: En una celda de concentración, el potencial celular estándar siempre será cero. Para obtener un potencial celular positivo (proceso espontáneo) el cociente de reacción Q debe ser <1. Q < 1 en este caso, por lo que el proceso es espontáneo.
¿Qué valor de Q para la celda de concentración anterior resultaría en un voltaje de 0.10 V? Si la concentración de ion zinc en el cátodo era de 0.50 M, ¿cuál era la concentración en el ánodo?
- Contestar
-
Q = 0.00042; [Zn 2 +] cat = 2.1\ times 10 −4 M.
Resumen
El trabajo eléctrico (w ele) es el negativo del producto de la carga total (Q) y el potencial celular (celda E). La carga total se puede calcular como el número de moles de electrones (n) veces la constante de Faraday (F = 96,485 C/mol e −). El trabajo eléctrico es el trabajo máximo que el sistema puede producir y así es igual al cambio en la energía libre. Así, cualquier cosa que se pueda hacer con o con un cambio de energía libre también se puede hacer a o con un potencial celular. La ecuación de Nernst relaciona el potencial celular en condiciones no estándar con el logaritmo del cociente de reacción. Las células de concentración explotan esta relación y producen un potencial celular positivo usando medias células que difieren solo en la concentración de sus solutos.
Ecuaciones Clave
- \(E^\circ_\ce{cell}=\dfrac{RT}{nF}\:\ln K\)
- \(E^\circ_\ce{cell}=\dfrac{\mathrm{0.0257\: V}}{n}\:\ln K=\dfrac{\mathrm{0.0592\: V}}{n}\:\log K \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
- \(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{RT}{nF}\:\ln Q \hspace{40px} \textrm{(Nernst equation)}\)
- \(E_\ce{cell}=E^\circ_\ce{cell}−\dfrac{\mathit{0.0257\: V}}{n}\:\ln Q=E^\circ_\ce{cell}−\dfrac{\mathrm{0.0592\: V}}{n}\:\log Q \hspace{40px} \mathrm{(at\: 298.15\:\mathit{K})}\)
- Δ G = − celda nFe
- \(ΔG^∘=−nFE^\circ_\ce{cell}\)
- \(w_\ce{ele}=w_\ce{max}=−nFE_\ce{cell}\)
Glosario
- célula de concentración
- celda galvánica en la que las dos medias celdas son iguales excepto por la concentración de los solutos; espontánea cuando la reacción global es la dilución del soluto
- trabajo eléctrico (w ele)
- negativo de carga total multiplicado por el potencial celular; igual a w max para el sistema, y así es igual al cambio de energía libre (Δ G)
- Constante de Faraday (F)
- carga sobre 1 mol de electrones; F = 96.485 C/mol e −
- Ecuación de Nernst
- ecuación que relaciona el logaritmo del cociente de reacción (Q) con potenciales celulares no estándar; puede usarse para relacionar constantes de equilibrio con potenciales celulares estándar