5.P: Problemas
- Page ID
- 81045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Preguntas sobre la revisión del concepto
1. ¿Cuáles son los supuestos (axiomas) de la teoría orbital molecular (MO)?
2. Explicar cualitativamente por qué la adición vectorial de orbitales atómicos crea orbitales moleculares (¿qué fenómeno físico subyacente se describe por la adición vectorial?).
3. Explicar cualitativamente por qué la teoría orbital molecular es adecuada para describir el enlace covalente.
4. ¿Cuáles son los tres criterios que determinan el grado de interacción covalente en la teoría de MO?
5. ¿Cuáles tres reglas determinan el grado de superposición orbital en la teoría de MO?
6. Explicar por qué la combinación de una órbita grande difusa y una orbital pequeña produce solo una interacción covalente débil.
7. Explique por qué las interacciones sigma entre orbitales atómicos suelen producir superposiciones orbitales más grandes que las interacciones pi.
8. Explicar por qué la combinación de orbitales de una misma energía conduce al mayor grado de interacción covalente.
9. ¿Qué se puede decir de la energía y ubicación de un orbital molecular de unión y antiunión que están hechos de orbitales atómicos de gran diferencia de energía?
10. La teoría de MO, aunque está diseñada para enlaces covalentes, también puede hacer declaraciones sobre la unión iónica. Explique por qué.
11. Explicar los principios de la SALC.
Problemas con la tarea
Sección 1
Ejercicio 1
¿Qué probablemente conducirá a la interacción covalente más pequeña?
a) Superposición de una órbita pequeña y otra grande.
b) Superposición de dos orbitales pequeños.
c) Superposición de dos orbitales grandes.
- Contestar
-
a) Superposición de una órbita pequeña y otra grande.
Ejercicio 2
¿Qué probablemente conducirá a la mayor interacción covalente?
a) superposición orbital en sigma-moda
b) superposición orbital en pi-fashion
c) superposición orbital en forma delta
- Contestar
-
a) superposición orbital en sigma-moda
Ejercicio 3
Construir cualitativamente los diagramas MO compuestos por
a) dos orbitales atómicos de 2s A y B de igual energía.
b) dos orbitales de 2 s átomos donde la energía orbital del átomo A es significativamente mayor que la de B. Si tanto el MO de enlace como el antienlace están llenos de electrones, ¿dónde se ubicarán principalmente los electrones de unión y antiunión? Explica brevemente tu decisión.
- Contestar
-

Ejercicio 4
Decidir por “inspección” cuál de las siguientes combinaciones de orbitales tienen las simetrías “correctas” para formar orbitales moleculares.
a) El orbital 2p x del primer átomo de N y el orbital 2p y del segundo átomo de N en la molécula N 2. El eje z se define como el eje de unión en N 2.
b) El F 2p x y el orbital H 1s en la molécula HF. El eje z se define como el eje de unión.
c) El orbital 2p z de F y el orbital 1s en la molécula HF. El eje z se define como el eje de unión.
- Contestar
-
a)
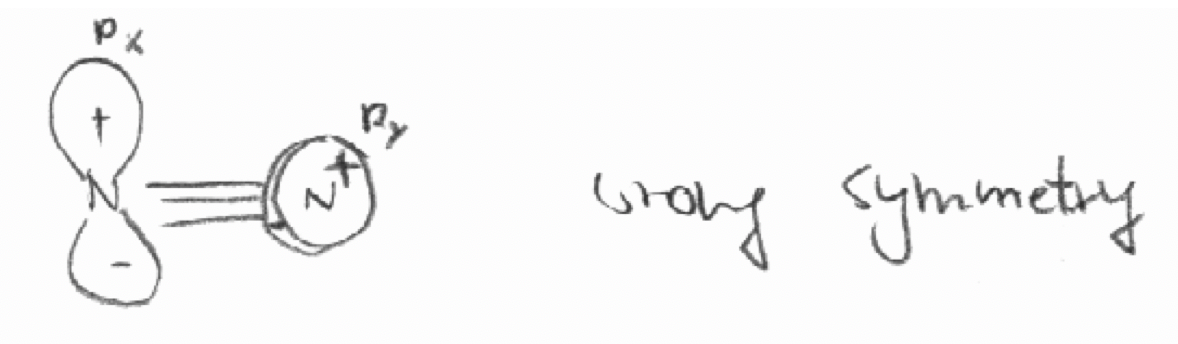
b)
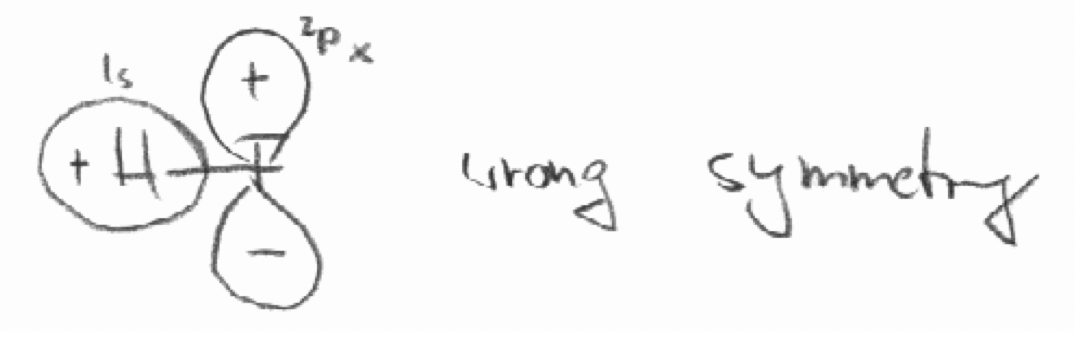
c)
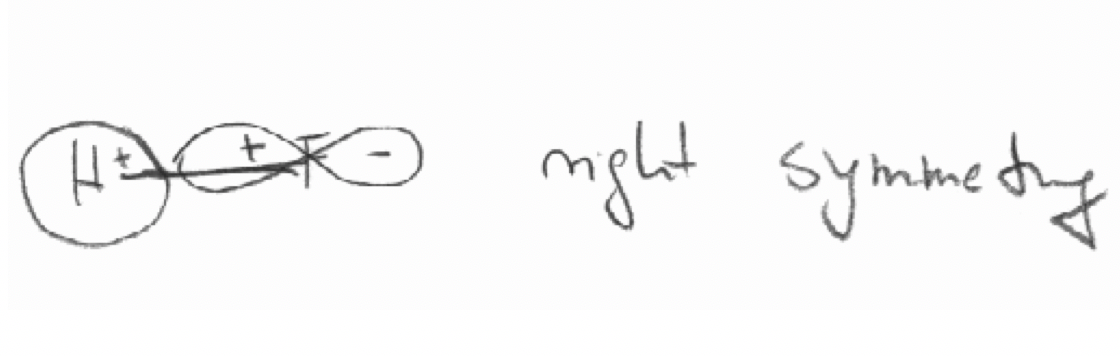
Ejercicio 5
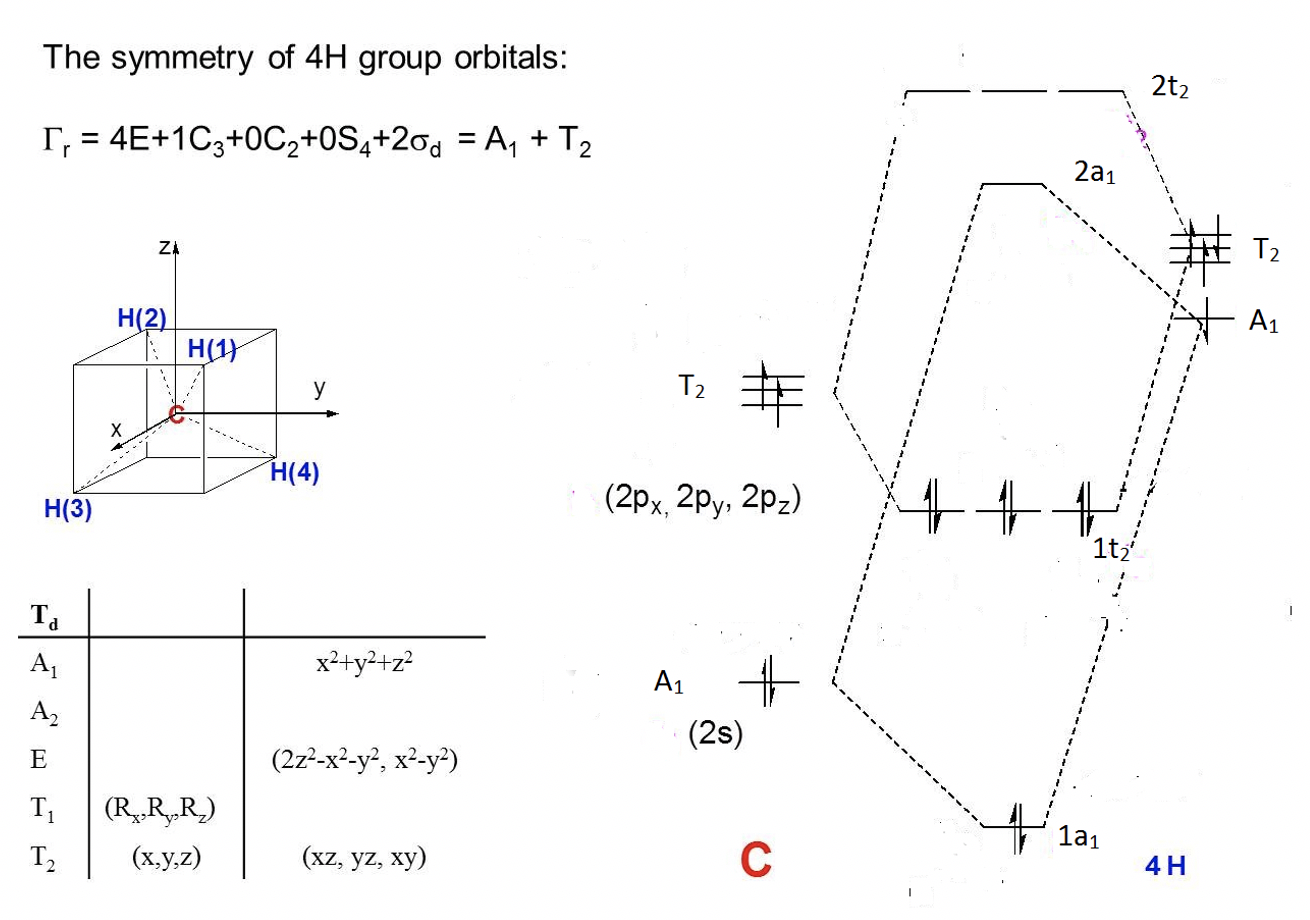
La molécula CH 4 pertenece al grupo puntual T d. Puedes encontrar la tabla de caracteres del grupo de puntos en internet.
a) Calcular la representación reducible para los orbitales del grupo ligando (LGO).
b) Calcular las representaciones irreducibles de los orbitales del grupo ligando (LGO).
c) Dibujar un diagrama orbital molecular cualitativo para CH 4.
- Contestar
-
Ejercicio 6
¿Cuáles son los tipos de simetría de los orbitales de átomos centrales en la molécula PCl 5?
- Contestar
- 1. Determinar grupo puntual de PCl 5. —> D 3h.
- 2. Decide cuáles son los orbitales de valencia del átomo central: 3s, 3p
- 3. Busca la tabla de personajes de D 3h, e.g., en internet. Encontrarás que sus simetrías son: A 1 '(3s), A 2 "(3p z), E' (3p x, 3p y)
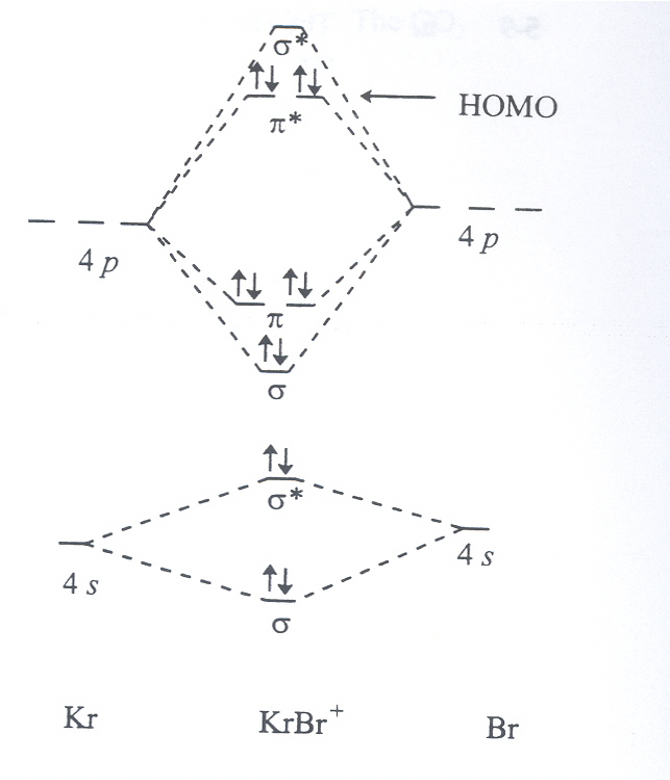
Ejercicio 7
Para la hipotética molécula BrKr +: ¿Hacia qué átomo está polarizado el HOMO? Explique brevemente por qué.
- Contestar
-

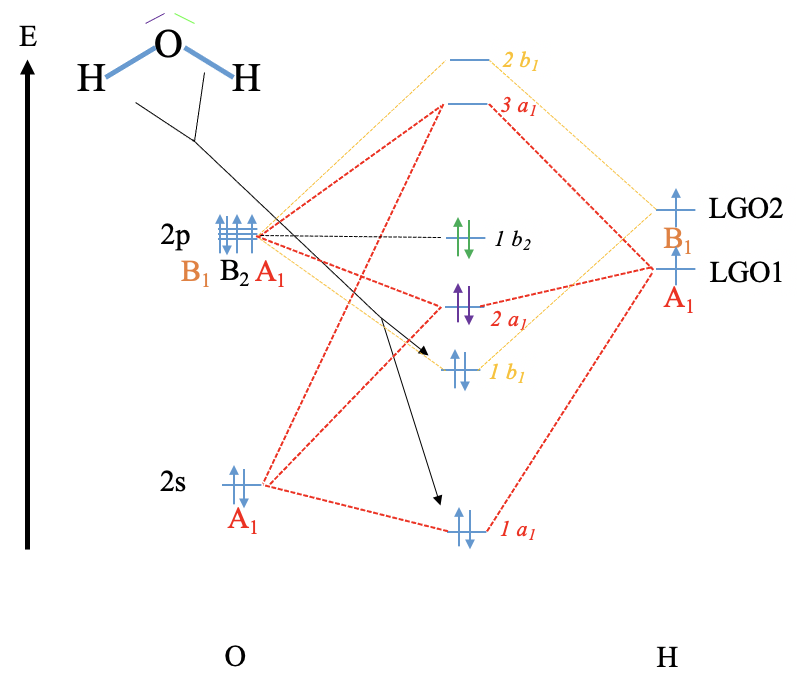
Ejercicio 8
Reconstruye el diagrama MO para agua y NH 3 (repite lo que hicimos en clase sin mirar tus notas (solo usa las tablas de caracteres respectivas).
- Contestar
-
Agua
NH 3
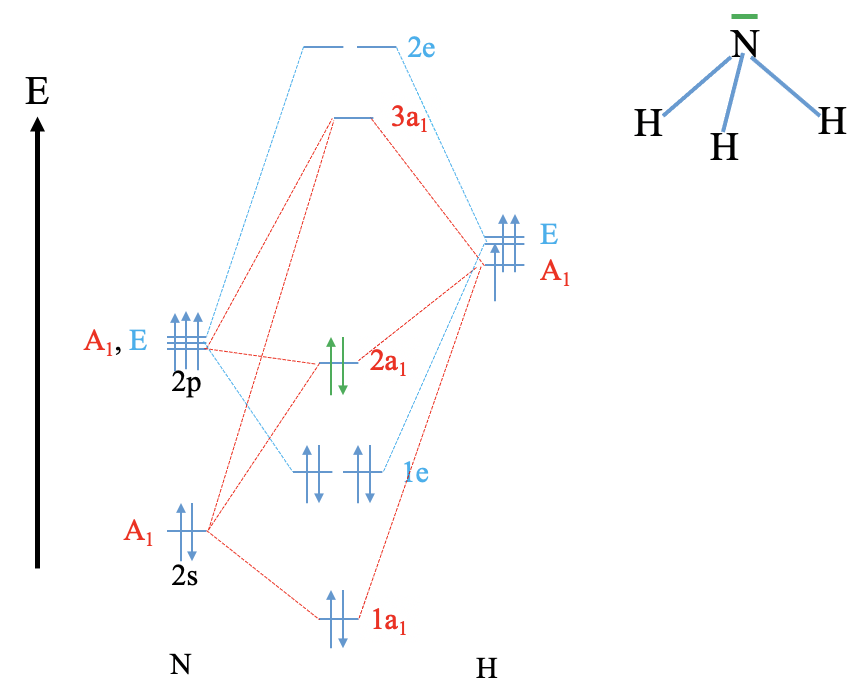
Un diagrama orbital molecular para una molécula diatómica (dos átomos) siempre tiene el mismo patrón básico.
- Dibuja una imagen de los niveles.
- Etiquetar cada nivel con σ, σ*, π, π*
- Contestar
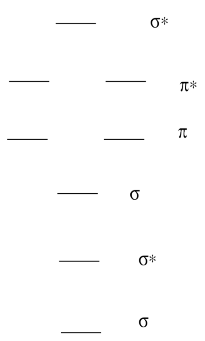
Un diagrama orbital molecular para una molécula diatómica (dos átomos) varía en el número de electrones. ¿Cómo se pueblan los electrones?
- Contestar
-
• Contar los electrones de valencia en la molécula. Ese es el número de electrones de valencia en cada átomo, ajustados para cualquier carga en la molécula. (por ejemplo, C 2 2 - tiene 10 electrones de valencia: 4 de cada carbono —eso es 8— y dos más para la carga 2-).
• Llene primero los electrones en los orbitales de menor energía.
• Los electrones pares después de todos los orbitales al mismo nivel de energía tienen un electrón.
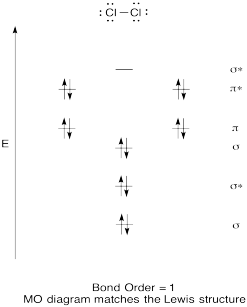
Construir un diagrama orbital molecular cualitativo para cloro, Cl 2. Comparar el orden de enlace con el visto en la estructura de Lewis (recuerde que un electrón en un orbital antienlace cancela la estabilización debido a la unión de un electrón en un orbital de enlace).
- Contestar
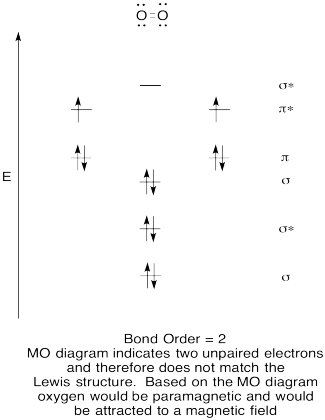
- Construir un diagrama orbital molecular cualitativo para oxígeno, O 2.
- Comparar el orden de unión con el visto en la estructura de Lewis.
- ¿De qué otra manera se compara esta imagen MO de oxígeno con la estructura de Lewis? ¿Qué te dicen las dos estructuras sobre el emparejamiento de electrones?
- Los compuestos que tienen todos sus electrones emparejados se denominan diamagnéticos. Aquellos con electrones desapareados se denominan paramagnéticos. Los materiales paramagnéticos son atraídos por un campo magnético, pero las cosas diamagnéticas no lo son. ¿Cómo esperarías que se comportara el oxígeno molecular?
- Contestar
-
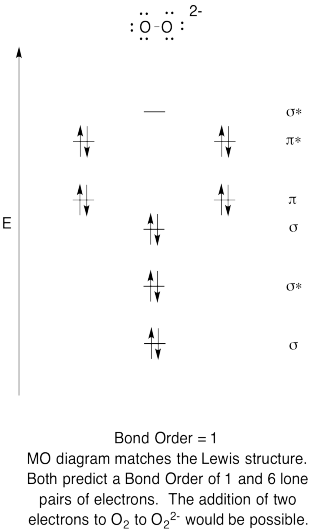
- Construir un diagrama orbital molecular cualitativo para anión peróxido, O 2 2 -.
- Comparar el orden de unión con el visto en la estructura de Lewis.
- ¿De qué otra manera se compara esta imagen MO de oxígeno con la estructura de Lewis? ¿Qué te dicen las dos estructuras sobre el emparejamiento de electrones?
- Basado en imágenes orbitales moleculares, ¿con qué facilidad cree que el dioxígeno podría reducirse a peróxido (mediante la adición de dos electrones)?
- Contestar
-
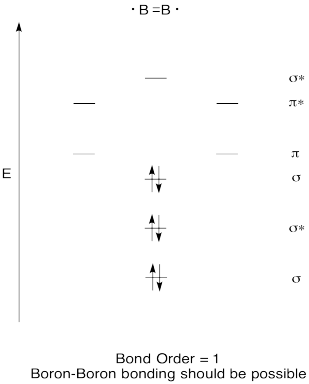
Construir un diagrama orbital molecular cualitativo para el diboro, B 2. ¿Crees que los enlaces boro-boro podrían formarse fácilmente, a partir de esta imagen?
- Contestar
-
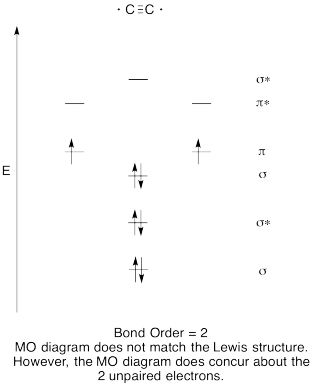
- Construir un diagrama orbital molecular cualitativo para dicarbono, C 2.
- Comparar el orden de unión con el visto en la estructura de Lewis.
- ¿De qué otra manera se compara esta imagen MO de oxígeno con la estructura de Lewis? ¿Qué te dicen las dos estructuras sobre el emparejamiento de electrones?
- Contestar
-
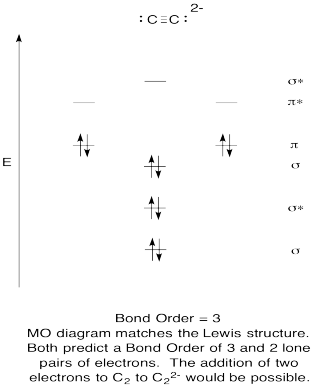
- Construir un diagrama orbital molecular cualitativo para anión acetiluro, C 2 2 -.
- Comparar el orden de unión con el visto en la estructura de Lewis.
- ¿De qué otra manera se compara esta imagen MO de oxígeno con la estructura de Lewis? ¿Qué te dicen las dos estructuras sobre el emparejamiento de electrones?
- Con base en imágenes orbitales moleculares, ¿con qué facilidad cree que el dicarbono podría reducirse a acetilido (mediante la adición de dos electrones)?
- Contestar
-
Hacer dibujos y notas para resumir el efecto de poblar orbitales antiadhesión.
- Contestar
-

Investigadores de Johns Hopkins reportaron recientemente la formación de Na 4 Al 2 en una descarga de arco pulsado (ponen mucha corriente eléctrica a través de una muestra de sodio y aluminio; Xinxing Zhang, Ivan A. Popov, Katie A. Lundell, Haopeng Wang, Chaonan Mu, Wei Wang, Hansgeorg Schnöckel, Alexander I. Boldyrev, Kit H. Bowen, Angewandte Chemie Edición Internacional, 2018, 57 (43), 14060-14064. Copyright 2018, John Wiley & Sons. Usado con permiso.).
- El compuesto es iónico. Explicar qué átomos forman los cationes, con base en tendencias periódicas.
- Por lo tanto, ¿qué átomos forman el anión?
- El anión es una molécula. ¿Cuál es la carga de esta molécula?
- Mostrar cómo calcular los electrones de valencia totales en este anión molecular.
- Dibuja una estructura de Lewis para este anión molecular.
- Construir un diagrama de nivel de energía orbital molecular diatómica para esta molécula. Marcar los niveles de energía (sigma, pi, etc.) y agregar el número correcto de electrones.
- Mostrar cómo calcular el orden de enlace en la molécula.
- Contestar
-
a) Na, porque el Na tiene un menor potencial de ionización (y una electronegatividad menor) que Al.
b) Al
c) 4-, porque hay cuatro Na +
d) total e - = 2 x 3 e - (por Al) + 4 e - (para la carga negativa) = 10 e-

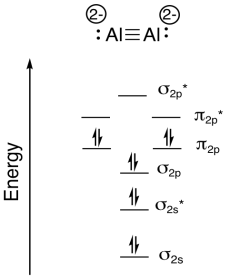
g)\(\textrm{bond order} = \frac{( \# bonding \: e^{-} - \# antibonding \: 3^{-})}{2} = \frac{8-2}{2}= 3\)
Dibuja el diagrama orbital molecular para (\(\ce{NO^-}\)).
- Contestar
-
Agrega textos aquí. No borre primero este texto.
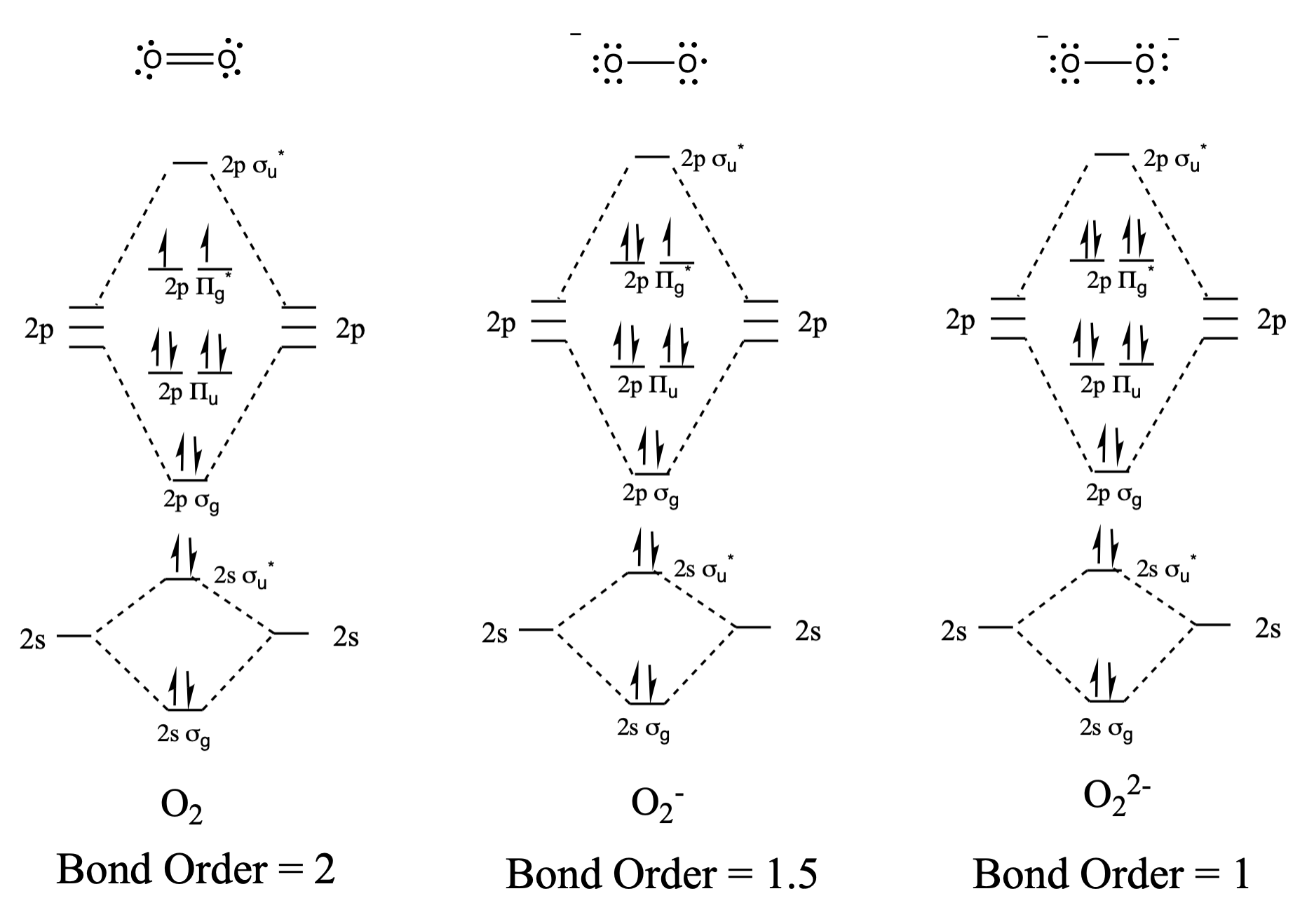
Dibuje y compare los diagramas orbitales moleculares con los diagramas de estructura de Lewis para\(\ce{O2}\),\(\ce{O2^-}\), y\(\ce{O2^2-}\).
- Contestar
-
Las estructuras de Lewis y los diagramas MO se muestran a continuación. En general, el orden de enlace derivado del diagrama MO concuerda con la estructura de Lewis para cada especie. En el caso de los dos iones, también concuerda el número de electrones desapareados de la teoría MO y la estructura de Lewis. En el caso del dioxígeno, sin embargo, existe una inconsistencia entre la representación de Lewis y el diagrama MO. Si bien la estructura de Lewis nos llevaría a creer que todos los electrones están emparejados, el diagrama MO indica paramagnetismo, con dos electrones desapareados. El diagrama MO explica el comportamiento magnético del dioxígeno.
Dibujar el diagrama orbital molecular para el ion hidróxido (\(\ce{OH^-}\)).
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Dibujar el diagrama orbital molecular para fluoruro de hidróxido (\(\ce{HF}\)).
- Contestar
-
Agrega textos aquí. No borre primero este texto.
Dibujar el diagrama orbital molecular para borano (\(\ce{BN}\)).
- Contestar
-
Agrega textos aquí. No borre primero este texto.
BH3
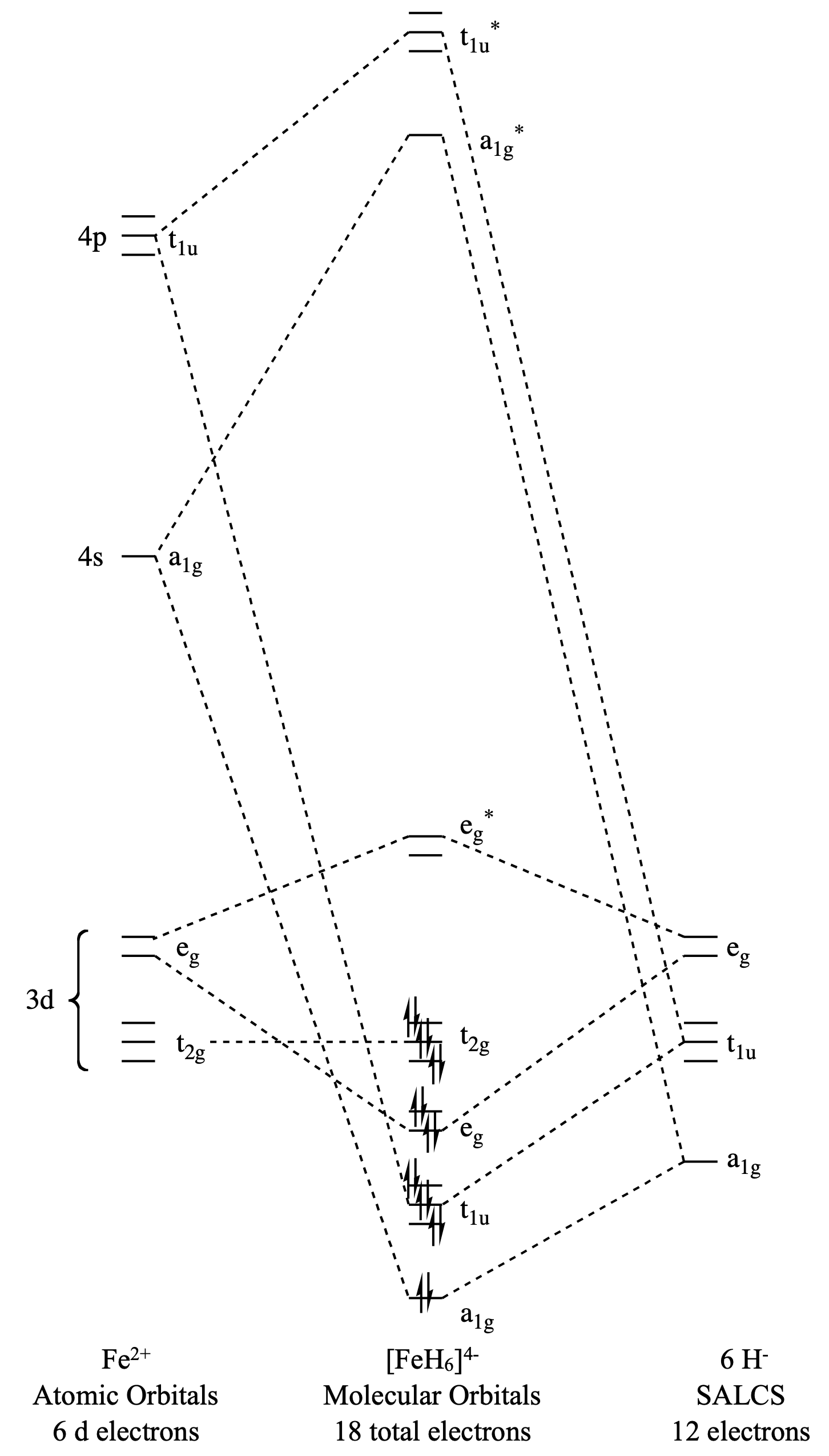
Dibuja el diagrama orbital molecular para (\(\ce{FeH6}\)).
- Contestar
-
Dibujar el diagrama orbital molecular para trifluoruro de boro (\(\ce{BF3}\)).
- ¿Qué es el orbital sin unión?
- ¿Qué son los orbitales HOMO y LUMO?
- ¿Por qué e' tiene 2 líneas de niveles de energía en comparación con a1', que solo tiene un nivel de energía de 1 línea?
- ¿Cuál es el orden de fianza\(\ce{BH3}\) en este diagrama MO?
- Contestar
-
A continuación se muestra el diagrama MO calculado.
- \(a_2''\)es el orbital solitario sin unión.
- El HOMO es el orbital\(a_2''\) no enlazante, el LUMO es un\(e'\) conjunto de unión de dos orbitales degenerados/
- \(e'\)es doblemente degenerado
- El orden de fianza es 3