1.3: Mediciones
- Page ID
- 77217
Las mediciones son una parte esencial para hacer las observaciones necesarias para desarrollar la ciencia. Varias mediciones se realizan comúnmente en la vida cotidiana, como se ilustra en la Fig. 1.3.1. Los valores medidos tienen dos componentes: un número y una unidad.
Números
Los números están compuestos por dígitos. Los dígitos son 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Los dígitos están escritos en fila en el número, por ejemplo, 123, lo que significa ciento veintitrés. Los números incluyen un punto decimal. Si el punto decimal no está marcado, se supone que está presente a la derecha del número. Por ejemplo, 123 es 123. por conversión, con el punto decimal mostrado en fuente roja.
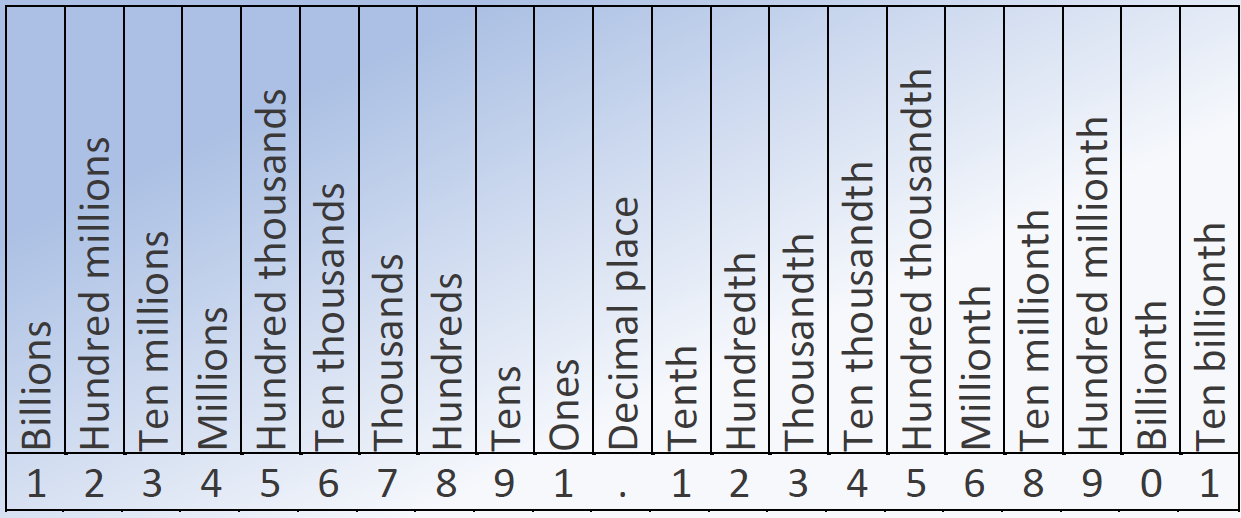
Valor posicional de un número
Los dígitos tienen valores posicionales. Los valores posicionales son relativos al punto decimal, es decir, el primer dígito a la izquierda del punto decimal es unos, el 2 º es decenas, el 3 rd es cientos, y así sucesivamente. El dígito 1 º a la derecha del punto decimal es décimo, segundo es centésima, 3 rd es milésima, y así, como se muestra en la Fig. 1.3.2. Por ejemplo, en 231.45, el dígito 2 es cientos, es decir, 200, 3 es decenas, es decir, treinta, 1 es unos, es decir uno, 4 es décimo, es decir, cuatro dividido por diez, y 5 es centésima, es decir cinco dividido por cien.
Signo de un número
Los números tienen signos, ya sea +ve o -ve, a la izquierda de un número, por ejemplo, -23.4 y +430. Por conversión, ningún signo significa +ve. Los signos son relativos a cero; el signo -ve significa que el número es menor que cero, y el signo +ve significa que el número es más que cero.
El número y los cálculos de inicio de sesión
Las reglas para el inicio de sesión en una respuesta calculada son las siguientes.
- Cuando se suman dos números positivos, la respuesta tiene un signo +ve, por ejemplo, 3+2 = 5.
- Cuando se suman dos números negativos, la respuesta tiene el signo —ve, por ejemplo, -4 + (-2) = -6.
- Cuando dos números que tienen signos opuestos suman, resta el número menor del número mayor, y la respuesta tiene el signo del número mayor. Por ejemplo, -5 +3 = -2.
- En la resta, cambia el signo del número restado y luego sigue las reglas de suma. Por ejemplo, restar 3 de 5:5- (+3) = 5-3 = 2. Tenga en cuenta que 3 se resta, y su signo cambió antes de la suma operativa. Otro ejemplo: restar -6 de 2:2- (-6) = 2+6 = 8
- Cuando dos números positivos se multiplican, la respuesta tiene un signo +ve, e.g., 2x3 = 6.
- Cuando dos números negativos se multiplican, la respuesta tiene un signo +ve, por ejemplo, (-4) x (-3) = 12.
- Cuando los dos números multiplicados tienen signos opuestos, la respuesta tiene un signo —ve, por ejemplo, (-3) x 2 = -6 y 4 x (-4) = -16.
- Cuando un número se divide por otro número, sigue reglas de multiplicación para el signo. Por ejemplo,\(\frac{-4}{-2}=2, \quad \frac{4}{2}=2, \quad\frac{-4}{2}=-2, \text { and } \frac{9}{-3}=-3\).
Cálculos porcentuales
El porcentaje (%) es la parte de cien, como se ilustra en la Fig. 1.3.3. El porcentaje se calcula como parte dividida por el total y luego se multiplica por cien, es decir:
\ begin {ecuación}
\ texto {porcentaje}\ %=\ frac {\ text {Monto parcial}} {\ text {Monto total}}\ veces 100\ nonumber
\ end {ecuación}
Calcular el porcentaje de aspirina si hay 81 mg de aspirina en una tableta de 325 mg?
Solución
parte = 81 mg aspirina, Total = 325 mg comprimido
Fórmula:\ begin {ecuación}
\ texto {porcentaje} =\ frac {\ texto {Cantidad parcial}} {\ texto {Monto total}}\ veces 100\ nonumber
\ end {ecuación}
Enchufa los valores en la fórmula y calcula:\ begin {ecuación}
\ text {Porcentaje} =\ frac {81\ mathrm {mg}\ texto {aspirina}} {325\ mathrm {mg}\ texto {tableta}}\ times 100=25\%\ text {aspirina}\ nonumber
\ end {ecuación}
Una pieza de joyería de oro de color verde de 18 quilates tiene 7.5 g de oro, 2.0 g de plata y 0.5 g de cobre. Calcular el porcentaje de oro en la joyería?
Solución
Parte = 7.5 g oro, Total = 7.5 g oro + 2.0 g plata + 0.5 g cobre = 10 g joyería.
Enchufa valores en la fórmula y calcula:\ begin {ecuación}
\ text {percentage} =\ frac {\ text {Monto parcial}} {\ text {Monto total}}\ times 100=\ frac {7.5\ mathrm {ggold}} {10\ mathrm {~g}}\ times 100=75\%\ mathrm {gold}\ nonumber
\ end {equation}
Escribir números en notación científica
A veces el número dado es demasiado grande o demasiado pequeño para ser fácilmente escrito, leído y captado. La notación científica es un enfoque para cambiar un número demasiado grande o demasiado pequeño en un número fácil de leer y escribir. Los siguientes pasos convierten un número dado a notación científica.
- Mueva el punto decimal hacia la derecha o hacia la izquierda, un dígito a la vez, hasta que el dígito más grande distinto de cero se convierta en el lugar de uno. Por ejemplo, mueve el decimal en 12,700,000 siete veces hacia la derecha
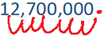para obtener 1.27, y mover el decimal en 0.000,006 seis veces hacia la izquierda
para obtener 6. Los números 1.27 y 6 obtenidos son los coeficientes de la notación científica. - El coeficiente se multiplica por 10 x, donde x es una potencia de diez. La potencia de diez es igual al número de veces que se movió el decimal. El signo de la potencia es +ve si el decimal se movió hacia la izquierda y -ve si el decimal se movió hacia la derecha. Por ejemplo, 12,700,000 en notación científica es 1.27 x 10 7, y 0.000.006 es 6 x 10 -6.
Unidades
Se miden las propiedades físicas como la masa, la longitud y la temperatura. El valor medido es una combinación de un número y una unidad, como se ilustra en la Fig. 1.3.4. Por ejemplo, la altura de una persona es de 1.83 metros, donde 1.83 es un número y un metro es una unidad.
Las unidades son cantidades definidas por la norma que los pueblos acuerdan utilizar como referencia.
Por ejemplo, el medidor se define como la distancia que recorre la luz en un vacío en\(\frac{1}{299,792,458}\) un segundo.
Sistemas de unidades
Existen diferentes conjuntos de unidades utilizadas en diferentes sistemas de unidades. Por ejemplo, 1.83 metros y 6.00 pies muestran el mismo valor de longitud pero usando una unidad de 'metro' del sistema internacional de unidades (SI) y 'pie' del sistema inglés de unidades. El sistema internacional de unidades (SI) es universalmente utilizado en el trabajo científico. Hay siete unidades base en el SI, como se indica en el Cuadro 1.
|
Medición |
Unidad |
Abreviatura |
|---|---|---|
|
Tiempo |
segundo |
s |
|
Largo |
medidor |
m |
|
Masa |
kilogramo |
kg |
|
Temperatura |
kelvin |
K |
|
Cantidad de sustancia |
mole |
mol |
|
Corriente eléctrica |
amperio |
A |
La siguiente sección se basa en la redefinición 2019 de las unidades base SI: https://en.Wikipedia.org/wiki/2019_redefinition _of_the_si_base_units #Kilogram, consultado el 2 de mayo de 2020
Tiempo
El tiempo es el progreso de la existencia y de los acontecimientos que ocurren en sucesión desde el pasado a través del presente hasta el futuro.
En tiempos antiguos, el dispositivo de medición de tiempo era el vidrio de arena de hora que se muestra en la Fig. 1.3.5. La unidad básica de tiempo es segundo (s), una unidad de tiempo estándar en todos los sistemas de medición. Otras unidades de tiempo son minuto (min) que es igual a 60 s, y hora que es igual a 60 min o 3600 s.
La duración de 9,192,631,770 periodos de la radiación correspondientes a la transición entre los dos niveles hiperfinos del estado fundamental del cesio 133 átomos a una temperatura de 0 K.
Largo
La longitud es una medida de distancia, es decir, una medida numérica de lo lejos que están los objetos o puntos.
La Fig. 1.3.6. ilustra el concepto de longitud. La unidad SI de longitud es un metro (m).
El medidor se define como la distancia que la luz recorre en un vacío en\(\frac{1}{299,792,458}\) un segundo.
Masa
La masa de un objeto es una medida de su inercia.
La inercia es la resistencia de cualquier objeto físico a cualquier cambio en su velocidad. La masa determina la fuerza de la atracción gravitacional de un objeto hacia otro objeto, una propiedad comúnmente utilizada en balanzas modernas para mediciones de masa, como se muestra en la Fig. 1.3.7. SI unidad de masa es el kilogramo (kg).
Definición anterior: La masa de un decímetro cúbico de agua en el punto de fusión del hielo.
Definición actual: Kilogramo (kg) se define tomando el valor numérico fijo de la constante de Planck h para ser 6.62607015×10 −34 cuando se expresa en la unidad kgm 2 s − 1.
Temperatura
La temperatura es una propiedad física de la materia que expresa picor o frialdad, como se ilustra en la Fig. 1.3.8.
La temperatura es una manifestación de la energía térmica de la materia, que es una fuente del flujo de energía en forma de calor de un objeto caliente a un objeto frío cuando están en contacto entre sí.
La unidad de temperatura SI es Kelvin (K).
Kelvin (K) se define tomando el valor numérico fijo de la constante de Boltzmann k para ser 1.380649×10 −23 cuando se expresa en la unidad kgm 2 s − 2 K − 1.
A 0 K, también llamado cero absoluto, es la temperatura de una materia a la que no se puede eliminar energía como calor de la materia. El punto de congelación del agua es 273.15 K, y el punto de ebullición del agua es 373.15 K.
Cantidad de sustancia
En química, la cantidad de sustancia (n) mide el número de entidades elementales especificadas. Las partículas elementales en química suelen ser átomos en el caso de elementos y moléculas o unidades de fórmula en el caso de compuestos. La unidad SI de la cantidad de una sustancia es un mol (mol).
El topo es exactamente 6.02214076×10 23 entidades elementales.
La Fig. 1.3.9 ilustra un mol de aluminio, cobre y carbono. La masa molar es la masa en gramos de un mol de esa sustancia, es decir, la masa de 6.02214076×10 23 átomos o moléculas. Por lo general, el número de partículas se muestra con cuatro cifras significativas, es decir, 6.022 x 10 23 átomos o moléculas en un mol de la sustancia.
Fuente: Información pública, foto: R. Press/NIST; diseño gráfico: N. Hanacek/NIST
Corriente eléctrica
La corriente eléctrica es el caudal de carga eléctrica más allá de un punto o una región.
Podría ser el flujo de electrones en cables eléctricos o el flujo de cationes y aniones en direcciones opuestas como en electrolitos, como se ilustra en la Fig. 1.3.10. La unidad de corriente SI es amperio (A).
El amperio (A) se define tomando la carga de un electrón (e) para ser 1.602176634×10 −19 culomb (C), donde C es equivalente a amperios-segundo (A.s).
Intensidad luminosa
La intensidad luminosa mide la potencia ponderada por longitud de onda emitida por una fuente de luz en una dirección particular por unidad de ángulo sólido.
El ángulo sólido se mide en esteradiano (sr), análogo al radián. El radián es un ángel plano que da la longitud de la circunferencia de un círculo, y el estereadiano es un ángulo 3D, como un cono, que da un área en la superficie de una esfera, como se muestra en la Fig. 1.3.11.
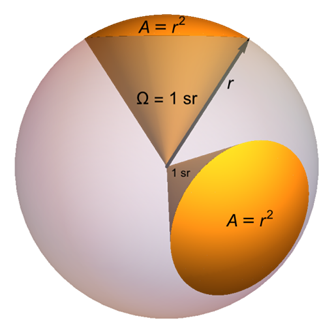
La unidad SI de intensidad luminosa en una dirección dada es Candela (cd).
La candela (cd) se define tomando el valor numérico fijo de la eficacia luminosa de la radiación monocromática de frecuencia 540 × 10 12 Hz, K cd, para que sea 683 cdsrw − 1, o cdsrkg − 1 m − 2 s 3, donde W es vatio —una unidad SI de potencia descrita por kg.m 2 .s -3.
Prefijos en SI
En varias situaciones, el número medido con la unidad base es demasiado grande o demasiado pequeño. Por ejemplo, la altura de una persona es cómoda de representar en el metro ya que la altura suele estar en un rango de 1 m a 2 m. Sin embargo, el diámetro de la tierra, es decir, 12,700,000 m, y el diámetro de los glóbulos rojos, es decir, 0.000,006 m, son demasiado grandes y demasiado pequeños, respectivamente. La unidad necesita ser revisada para que el número con ella sea fácil de leer y escribir.
Los prefijos se utilizan en SI para aumentar o disminuir la unidad base por orden de decenas.
Por ejemplo, kilo (k) significa mil veces, es decir, 1 km significa 1000 m y 1 kg significa 1000 g. Del mismo modo, micro (µ) significa una millonésima vez, es decir, 1 µm es 10 -6 m, y 1 µg es 10 -6 g. En la Tabla 2 se enumeran los prefijos de uso común en SI.
|
Prefijo |
Medios |
Abreviatura |
|---|---|---|
|
Gega |
10 9 |
G |
|
Mega |
10 6 |
M |
|
Kilo |
10 3 |
k |
|
Deci |
10 -1 |
d |
|
Centi |
10 -2 |
c |
|
Mili |
10 -3 |
m |
|
Micro |
10 -6 |
µ |
|
Nano |
10 -9 |
n |
|
Pico |
10 -12 |
p |
Se puede definir y usar una nueva unidad si no hay un prefijo apropiado disponible en SI para algún tipo específico de medición. Por ejemplo, el diámetro de los átomos varía en el rango de 1 x 10 -10 m a 5 x 10 -10 m, donde el prefijo pico (p, 10-12) es demasiado pequeño, y el prefijo nano (n, 10-9) es grande. Una nueva unidad llamada angstrom (Å) se define como 1Å = 10 -10 m para reportar diámetro atómico y distancias interatómicas.
Unidades derivadas
Las unidades en SI distintas de las siete unidades base son Unidades Derivadas obtenidas combinando las unidades base.
Por ejemplo, La unidad SI de volumen es metro-cubo (m 3), igual al espacio ocupado por un cubo de 1m en cada borde, como se ilustra en la Fig. 1.3.12.
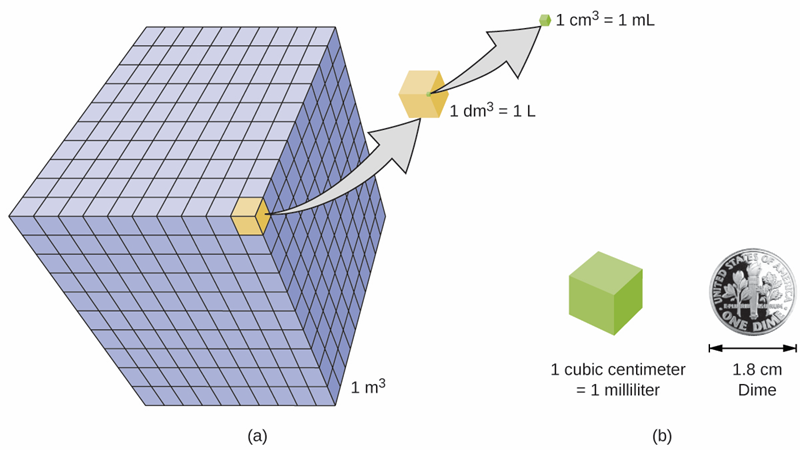
Por lo general, el volumen se reporta en decímetro-cubo (dm 3), comúnmente conocido como litro (L). Un litro es un volumen ocupado por un cubo que es un dm en cada borde. Otra unidad de volumen comúnmente utilizada es el centímetro-cubo (cm 3), que también se llama cc o mL. Un mL es el volumen ocupado por un cubo que mide un cm en cada borde. El dm 3 es una milésima de m 3, y cm 3 es la milésima de dm 3, es decir, 1000 dm 3 = 1 m 3, y 1000 cm 3 = 1 dm 3, como se ilustra en la Fig. 1.3.11.
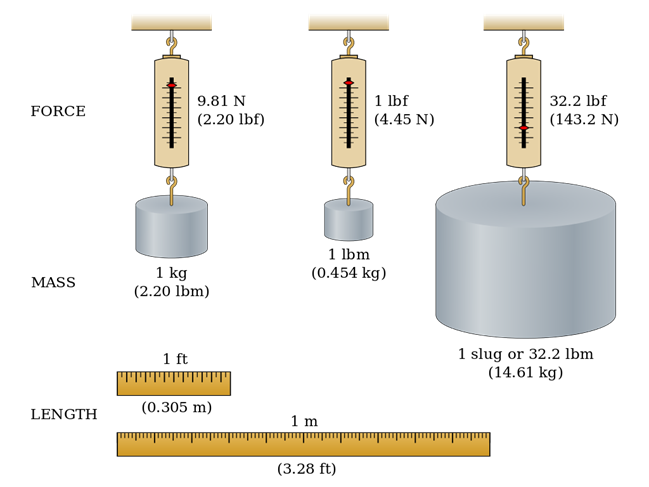
Relación de unidades SI con sistema métrico e inglés de unidades
El SI se desarrolló a partir del sistema métrico. Algunas unidades básicas son diferentes, pero ambos sistemas tienen mucho en común, usando los mismos prefijos. El sistema inglés de unidades utiliza un conjunto diferente de unidades excepto la unidad de tiempo común. En el Cuadro 3 se comparan las unidades de medida estándar en los tres sistemas de medición.
|
Cantidad |
Unidad inglesa |
Unidad métrica |
Unidad SI |
Relaciones |
|---|---|---|---|---|
|
Masa |
Libra (lb) |
Gramo (g) |
Kilogramo (kg) |
1 kg = 2.205 lb 1 kg = 1000 g |
|
Largo |
Pie (ft) |
Medidor (m) |
Medidor (m) |
1 m = 3.281 ft |
|
Volumen |
Cuarto (qt) |
Litro (L) |
Metro Cúbico (m 3) |
0.946 L = 1 qt 1 m 3 = 1000 L |
|
Energía |
caloría (cal) |
caloría (cal) |
Joule (J) |
4.184 J = 1 cal |
|
Temperatura |
Grado Fahrenheit (°F) |
Grado Celsius (°C) |
Kelvin (K) |
°F = (1.8 × °C) + 32 K = °C + 273.15 |