5.4: Actividad óptica
- Page ID
- 76446
Los dos enantiómeros son imágenes especulares entre sí. Son muy parecidos y comparten muchas propiedades en común, como el mismo b.p., m.p., densidad, color, solubilidad etc. De hecho, el par de enantiómeros tiene las mismas propiedades físicas excepto la forma en que interactúan con la luz polarizada plana.
En luz normal, el campo eléctrico oscila en todas las direcciones. Cuando la luz normal pasa a través de un filtro polarizador, solo la luz que oscila en un solo plano puede pasar, y la luz resultante que oscila en una sola dirección se llama luz polarizada en plano.
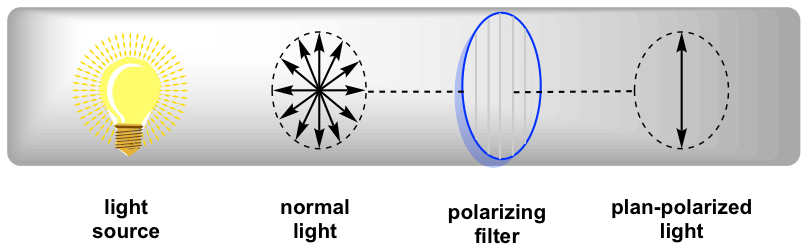
Cuando la luz polarizada en plano interactúa con moléculas quirales, el plano de polarización será rotado por las sustancias quirales. Fue descubierto por primera vez por Jean-Baptiste Biot en 1815 que algunas sustancias orgánicas naturales, como el alcanfor, son capaces de rotar el plano de polarización de la luz polarizada en el plano. También señaló que algunos compuestos giraban el plano en sentido horario y otros en sentido antihorario. Estudios posteriores indican que la rotación es causada por la quiralidad de las sustancias.
La propiedad de que un compuesto pueda rotar el plano de polarización de la luz polarizada en el plano se denomina actividad óptica, y el compuesto con dicha actividad se etiqueta como activo óptico. El estereoisómero que es activo óptico también se denomina isómero óptico.
El compuesto quiral es activo óptico. El compuesto aquiral es óptico inactivo.
La muestra que contiene un compuesto quiral gira el plano de polarización de la luz polarizada plana, la dirección y los ángulos de rotación dependen de la naturaleza y concentración de las sustancias quirales. Los ángulos de rotación se pueden medir mediante el uso de polarímetro (más adelante en esta sección).
Para un par de enantiómeros con la misma concentración, bajo las mismas condiciones, giran el plano de polarización con los mismos ángulos pero en sentido opuesto, uno es en sentido horario y el otro en sentido antihorario.
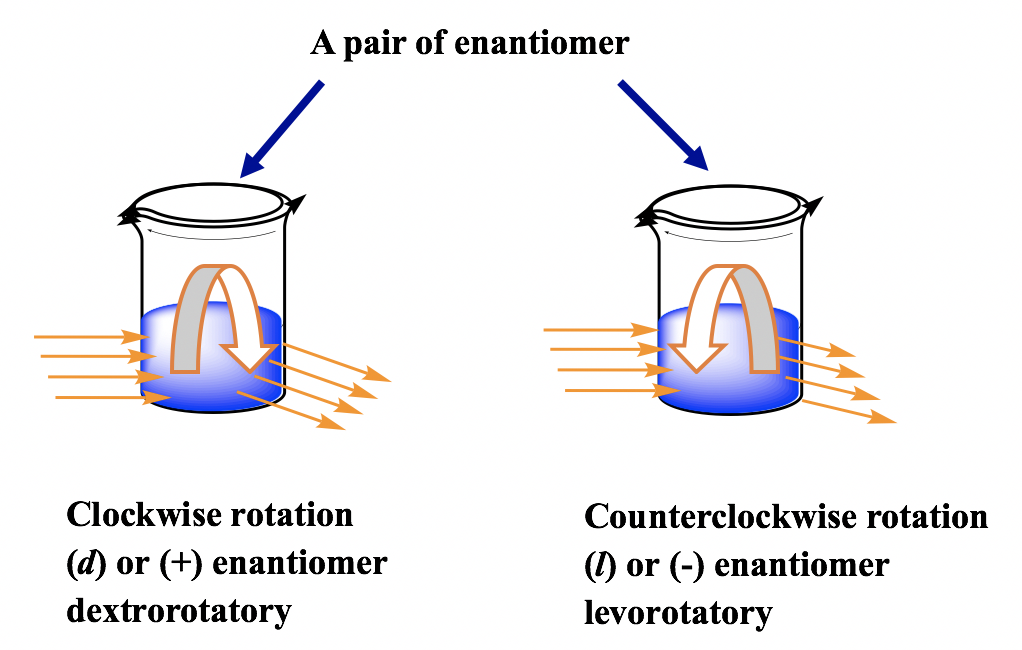
El enantiómero gira el plano de polarización en sentido horario se dice que es dextrorrotatorio (latín, significa a la derecha), y etiquetado con el prefijo (d) o (+). El enantiómero gira el plano de polarización en sentido antihorario se dice que es levorrotatorio (latín, significa a la izquierda), y etiquetado con el prefijo (l) o (—). Los d/l (o +/-) indican la dirección en la que un compuesto activo óptico gira el plano de polarización de la luz polarizada en el plano, que se tiene que determinar por experimento para medir la rotación óptica. El símbolo d/l (o +/ —) no tiene nada que ver con R/S. R/S indica la disposición de los grupos alrededor del centro de quiralidad, que se puede determinar conociendo la disposición espacial exacta de los grupos. Eso significa que el compuesto con configuración R puede ser d o l, y el compuesto con configuración S también puede ser d o l. Para los ejemplos siguientes, ambos compuestos son el isómero S, pero uno es d (+) y el otro es l (-).
Lo único que podemos estar seguros es que para un par de enantiómeros, si un enantiómero se ha determinado como d, entonces el otro enantiómero debe ser l, y viceversa.
Medición de Rotación Óptica
El polarímetro es el instrumento que mide la dirección y los ángulos de rotación de la luz polarizada en el plano. La luz polarizada en plano pasa a través del tubo de muestra que contiene la solución de muestra, y el ángulo de rotación será recibido y registrado por el analizador, como se resume en la Fig. 5.4c.
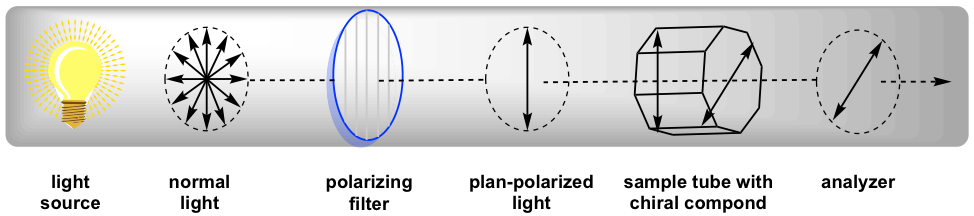
Dado que los resultados de la medición varían con la longitud de onda de la luz que se utiliza, la luz específica de un espectro atómico de sodio con la longitud de onda de 589 nm, que se llama la línea D de sodio, se usa para la mayoría de los polarímetros. El grado de rotación medido por el polarímetro se denomina rotación observada (α), y la rotación observada depende de la longitud del tubo de muestra, concentración de la muestra y temperatura.
Para comparar la rotación óptica entre diferentes compuestos bajo condiciones consistentes,
se utiliza la rotación específica. La rotación específica es la rotación causada por una solución con concentración de 1.0 g/mL en un tubo de muestra de 1.0 dm de longitud. La temperatura suele ser de 20°C. Con base en esta definición, la rotación específica se puede calcular a partir de la rotación observada aplicando la fórmula:
Tenga en cuenta: En esta fórmula, la unidad de concentración (g/mL) y la longitud del tubo de muestra (dm) no son las unidades con las que estamos familiarizados. Además, la unidad de la rotación específica está en grado (°), no es necesario preocuparse por la cancelación de unidades en esta fórmula.
Ejemplos: Calcular la rotación específica
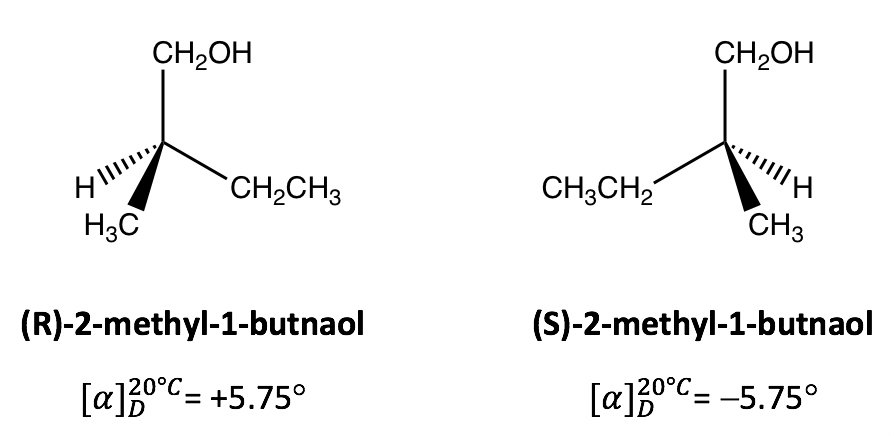
La rotación observada de 10.0g de (R) -2-metil-1-butnaol en 50ml de solución en un tubo polarímetro de 20 cm es de +2.3° a 20 °C, ¿cuál es la rotación específica del compuesto?
Solución
La rotación específica es la propiedad característica de un compuesto activo óptico. Los valores de rotación específicos de la literatura del compuesto auténtico pueden utilizarse para confirmar la identidad de un compuesto desconocido. Para el ejemplo aquí, si se ha medido que la rotación específica de (R) -2-metil-1-butnaol es de +5.75°, entonces podemos decir que el otro enantiómero (S) -2 -metil-1-butnaol debe tener la rotación específica de -5.75°, sin necesidad de realizar más mediciones.
Actividad óptica de diferentes muestras
Cuando una muestra bajo medición solo contiene un enantiómero, esta muestra se denomina enantioméricamente pura, significa que solo un enantiómero está presente en la muestra.
La muestra también puede consistir en una mezcla de un par de enantiómeros. Para dicha muestra de mezcla, el valor de rotación observado de la mezcla, junto con la información de la rotación específica de uno de los enantiómeros permiten calcular el porcentaje (%) de cada enantiómero en la mezcla. Para hacer dicho cálculo, se necesitará el concepto de exceso de enantiómero (ee). El exceso enantiomérico (ee) indica cuánto hay un exceso de un enantiómero en la mezcla, y se puede calcular como:
Utilizaremos una serie de ejemplos hipotéticos en la siguiente tabla para una explicación detallada.
| Si la rotación específica de un (+) -enantiómero es +100 °, entonces la rotación observada de las siguientes muestras son (supongamos que el tubo de muestra tiene la longitud de 1 dm, y la concentración para cada muestra es de 1.0 g/mL): | ||
| Número de muestra |
Muestra |
Rotación observada (º) |
| 1 | enantiómero puro (+) | +100 |
| 2 | Enantiómero (-) puro | -100 |
| 3 | Mezcla racémica de 50% (+) -enantiómero
y 50% (-) -enantiómero |
0 |
| 4 | Mezcla de 75% (+) -enantiómero y 25% (-) -enantiómero |
+50 |
| 4 |
Mezcla de 20% (+) -enantiómero y 80% (-) -enantiómero
|
-60 |
La muestra #1 y #2 son sencillas.
La muestra #3 es para una mezcla con igual cantidad de dos enantiómeros, y dicha mezcla se denomina mezcla racémica o racemato. Las mezclas racémicas no rotan el plano de polarización de la luz polarizada plana, eso significa que las mezclas racémicas son ópticas inactivas y tienen la rotación observada de cero! Esto se debe a que por cada molécula en la mezcla que gira el plano de polarización en una dirección, hay una molécula enantiomérica que gira el plan de polarización en la dirección opuesta con el mismo ángulo, y la rotación se cancela. Como resultado neto, no se observa rotación para la mezcla racémica global. El símbolo (±) a veces se usa para indicar que una mezcla es mezcla racémica.
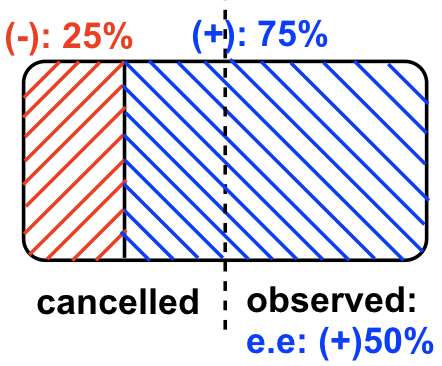
Muestra #4, el enantiómero (+) está en exceso. Dado que hay 75% (+) -enantiómero y 25% (-) -enantiómero, el valor de exceso enantiomérico (ee) del enantiómero (+) es 75% — 25% = 50%, esto también se puede calcular por la fórmula: ee =
En esta muestra de mezcla, la rotación del enantiómero (-) se cancela por la rotación causada por parte del enantiómero (+), por lo que la rotación neta total observada depende de la cantidad de “cantidad neta” de enantiómero (+) presente. Esto se puede mostrar mediante el diagrama a continuación que ayuda a entender.
Muestra #5, el enantiómero (-) está en exceso, y debido a que hay 80% (-) -enantiómero y 20% (+) -enantiómero, el valor de exceso enantiomérico (ee) del enantiómero (-) es 80% — 20% = 60%, esto también se puede calcular por la fórmula: ee =
Tenga en cuenta: para calcular el valor e.e, no es necesario incluir el signo del ángulo de rotación, siempre y cuando tenga en cuenta que el signo (+ o —) de la rotación observada indica que qué enantiómero está en exceso.
Ejercicios 5.6
Respuestas a las preguntas de práctica Capítulo 5
Ejemplos: Un nivel avanzado de cálculo
El enantiómero (+) de un compuesto tiene rotación específica ([α] 20 D) de +100°. Para una muestra (1 g/ml en célula de 1dm) que es una mezcla de enantiómeros (+) y (-), la rotación observada α es -45°, ¿cuál es el porcentaje de enantiómero (+) presente en esta muestra?
Solución
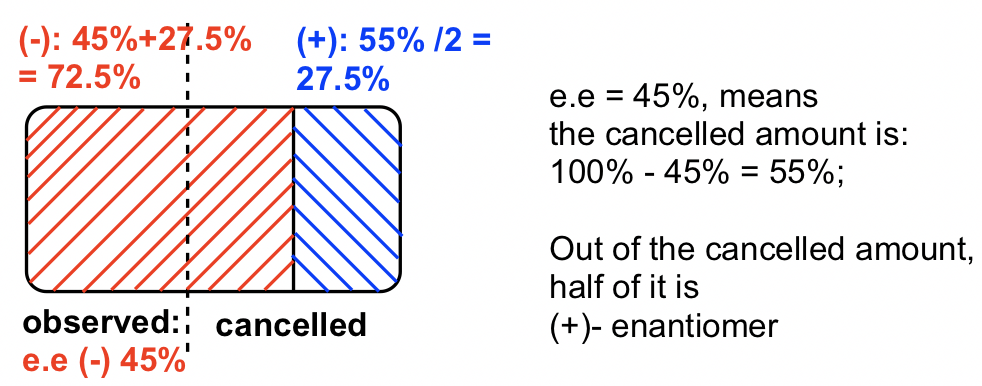
La rotación observada es en “-”, por lo que el enantiómero (-) está en exceso.
ee del enantiómero (-) es:
A partir de aquí, veremos dos formas de resolver ese tipo de preguntas:
Método I: resolver álgebra
“El% del enantiómero (-) se establece como “" x "”; el% del enantiómero (+) se establece como “" y "”
x + y = 100%
x — y = 45%
Resolver x = 72.5%; y = 27.5%;
Por lo que hay 72.5% (-) -enantiómero y 27.5% de (+) -enantiómero en la muestra.
Método II: usando diagrama, la respuesta es en color azul, hay 27.5% de enantiómero (+).
Quiralidad y Propiedades Biológicas
Aparte de la diferencia de actividad óptica, los diferentes enantiómeros de una molécula quiral suelen mostrar diferentes propiedades cuando interactúan con otras sustancias quirales. Esto se puede entender usando el ejemplo análogo de colocar una mano en el guante respectivo: la mano derecha solo cabe en el guante derecho, y se siente raro e incómodo si usas el guante izquierdo en la mano derecha. Esto se debe a que tanto la mano derecha como el guante derecho son quirales. Un objeto quiral solo encaja en un entorno quiral específico.
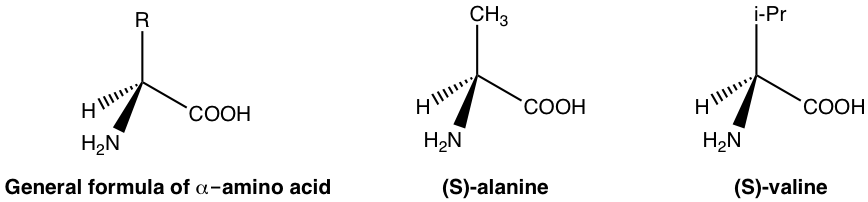
En el cuerpo humano, las funciones biológicas son moduladas por una gran cantidad de enzimas y receptores. Las enzimas y los receptores son esencialmente proteínas, y las proteínas están compuestas por aminoácidos. Los aminoácidos son ejemplos de sustancias quirales que existen naturalmente. Con la fórmula general dada a continuación, el carbono con grupo amino (NH 2) es el centro de quiralidad (asimétrico) para la mayoría de los aminoácidos, y solo existe un enantiómero (generalmente S-enantiómero) en la naturaleza. A continuación se dan algunos ejemplos de aminoácidos con la fórmula general.
Debido a que los aminoácidos son quirales, las proteínas son quirales por lo que las enzimas y los receptores también son quirales. Por lo tanto, la enzima o receptor forman el ambiente quiral en el cuerpo humano que distingue entre enantiómero R o S. Dicha selectividad se puede ilustrar mediante el diagrama simple a continuación.
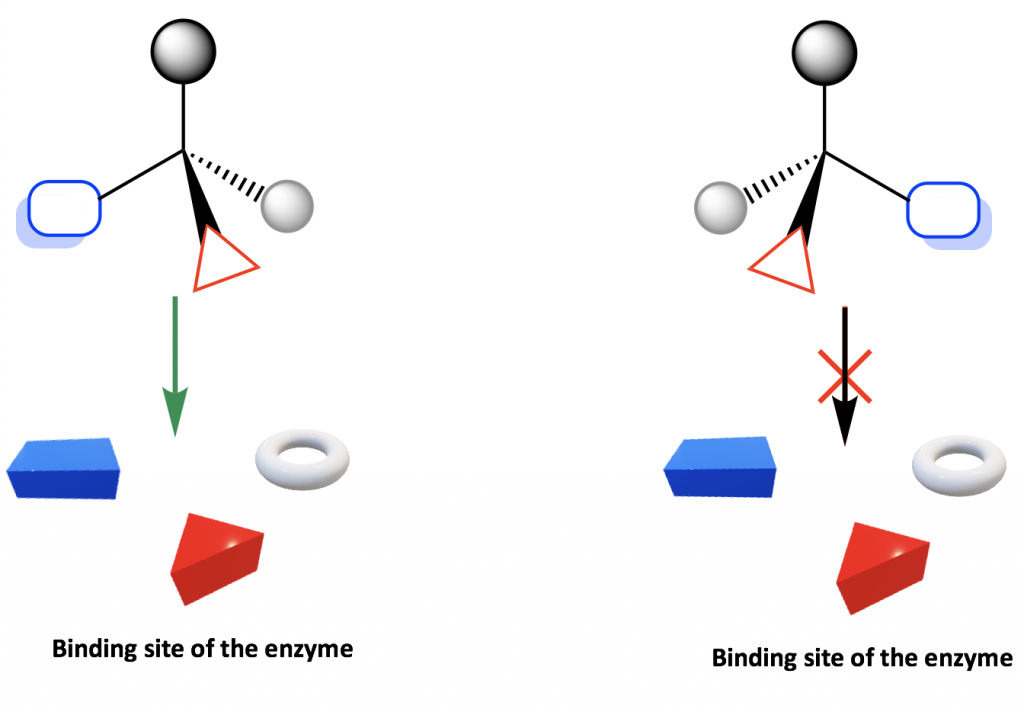
El sitio de unión de la enzima o receptor es quiral, por lo que solo se une con el enantiómero cuyos grupos están en las posiciones adecuadas para encajar en el sitio de unión. Como se muestra en el diagrama, solo un enantiómero se une con el sitio, pero no con el otro enantiómero.
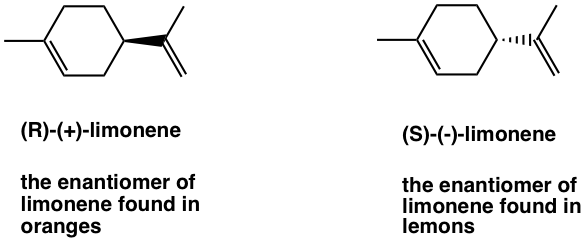
Un par de ejemplos comunes para mostrar tal selectividad de unión de diferentes enantiómeros pueden incluir limoneno y carvona.
El limoneno tiene dos enantiómeros, y huelen totalmente diferentes al ser humano porque interactúan con diferentes receptores que se localizan en las células nerviosas de la nariz. El (R) - (+) -limoneno es responsable del olor a naranja, y el (S) - (-) -limoneno le da el poco olor a limón.
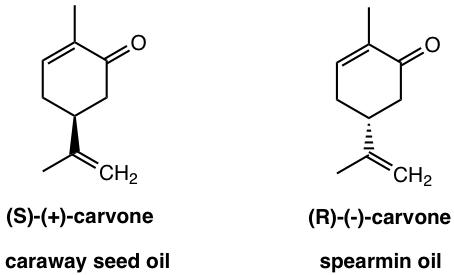
Si te gusta el pan de comino, eso se debe a que la (S) - (+) -carvona; y la (R) - (-) -carvona que se encuentra en el aceite de menta verde da olor muy diferente.
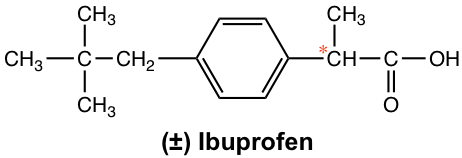
En muchos medicamentos se encuentran ejemplos más dramáticos de cómo la quiralidad juega un papel importante en las propiedades biológicas. Para el medicamento antiinflamatorio común de venta libre ibuprofeno (Advil), por ejemplo, solo el enantiómero (S) es el agente activo, mientras que el enantiómero (R) no tiene ninguna acción antiinflamatoria. Afortunadamente, el enantiómero (R) no tiene ningún efecto secundario dañino y se convierte lentamente en el enantiómero (S) en el cuerpo. El ibuprofeno se comercializa generalmente en forma de racemato.
El tema de los fármacos quirales (el fármaco contiene un solo enantiómero, no como racemato) no estuvo en la atención de la industria del descubrimiento de fármacos hasta 1960. En ese entonces, los fármacos se aprobaron en forma racemato si un centro de quiralidad involucraba, y no hubo más estudio sobre la diferencia biológica en diferentes enantiómeros. Todos estos fueron cambiados por el trágico incidente de la talidomida. La talidomida era un medicamento que se vendía en más de 40 países, principalmente en Europa, a principios de los sesenta como auxiliar para dormir y a las mujeres embarazadas como antiemético (fármaco que previene el vómito) para combatir las náuseas matutinas. No se reconoció en ese momento que solo el enantiómero R tiene la propiedad, mientras que el enantiómero S era un teratógeno que causa deformaciones congénitas. El medicamento se comercializó como una mezcla racémica y provocó que alrededor de 10 mil niños hubieran sido dañados hasta que fue retirado del mercado en noviembre de 1961. Sin embargo, este medicamento no fue aprobado en EU, atribuido a la doctora Frances O. Kelsey, quien era médica de la FDA (Food and Drug Administration) en ese momento y había insistido en pruebas de adición sobre algunos efectos secundarios. Miles de vidas fueron salvadas por la doctora Kelsey, y fue galardonada con la medalla del Presidente en 1962 por impedir la venta de talidomida.
