Inicio
Química
Química Orgánica
Reacciones radicales de los carbohidratos I: estructura y reactividad de los radicales carbohidrato
7: Filicidad Radical
II. Polaridades de enlace, energías de disociación de enlaces y constantes de velocidad para reacciones de abstracción de hidrógeno

II. Polaridades de enlace, energías de disociación de enlaces y constantes de velocidad para reacciones de abstracción de hidrógeno

Última actualización
Guardar como PDF

Page ID: 79560

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las polaridades de enlace, las energías de disociación de enlaces y las constantes de velocidad para la abstracción de átomos de hidrógeno unidos a estaño, silicio, azufre, selenio y carbono se dan en la Tabla 1. Según los valores de electronegatividad de Pauling, el hidrógeno tiene una pequeña carga negativa cuando se une al estaño o al silicio y una pequeña carga positiva cuando se une al azufre, selenio o carbono. La información del Cuadro 2 muestra que para cada tipo de enlace, la constante de velocidad para la abstracción de átomos de hidrógeno por radicales simples primarios, secundarios y terciarios centrados en carbono es casi la misma.

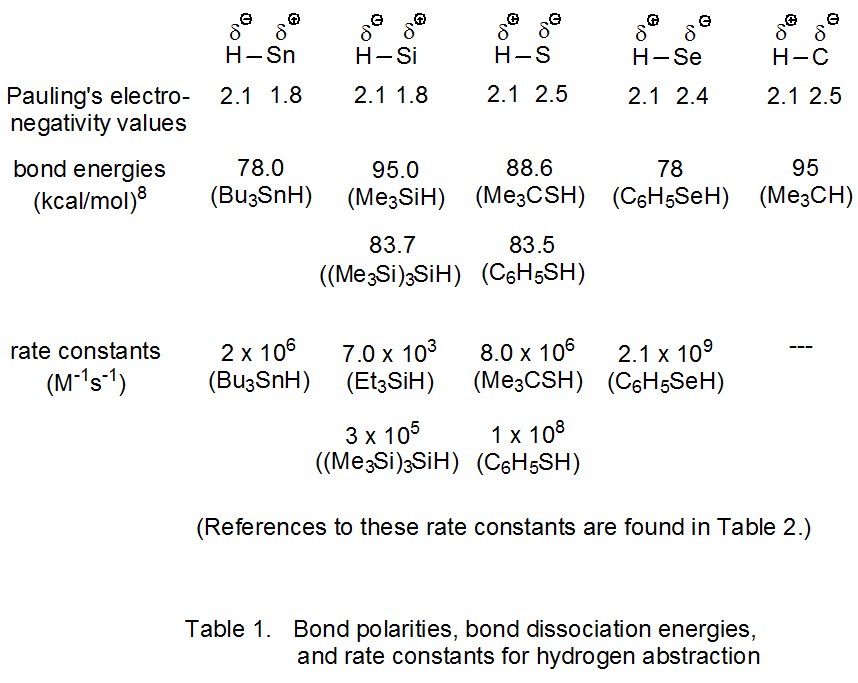
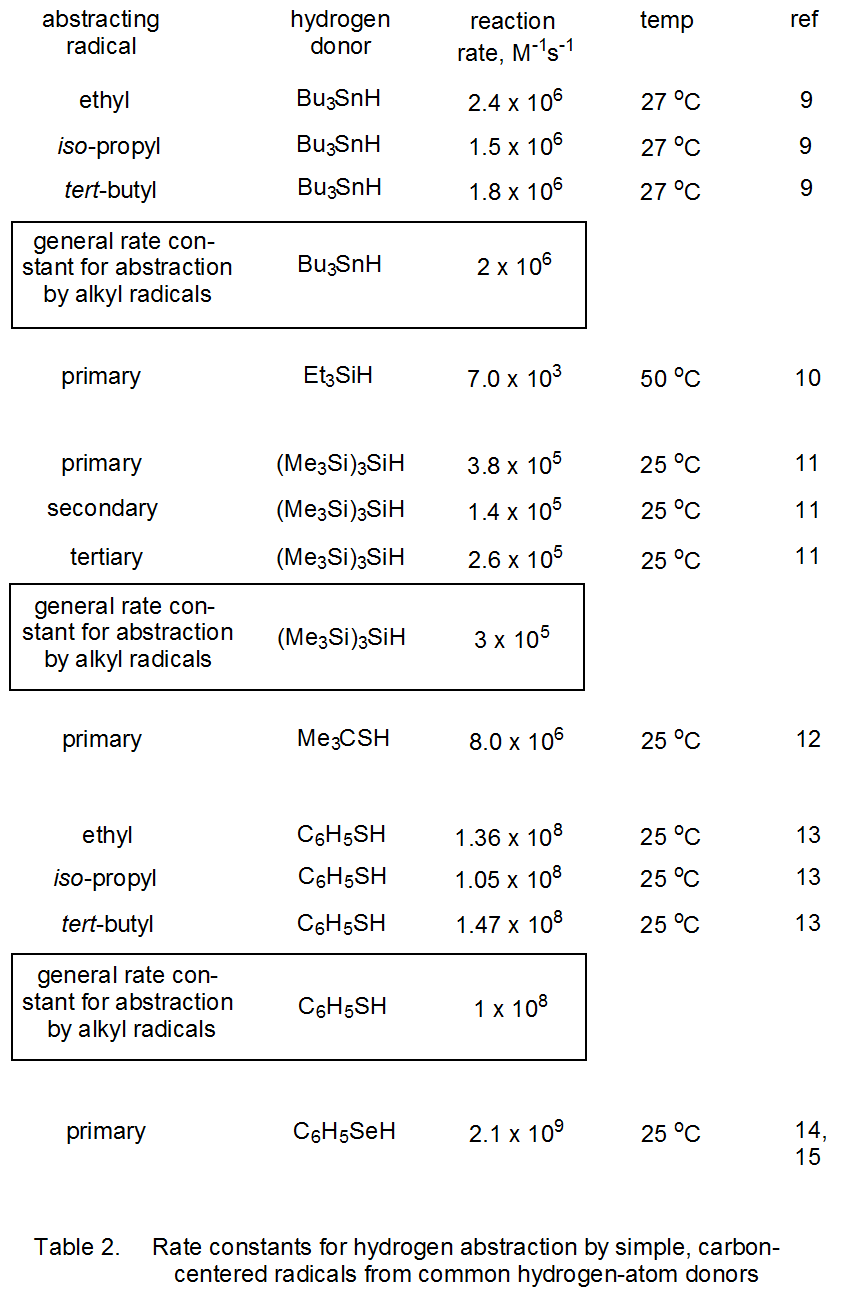
Cuando se utilizan las energías de disociación de enlaces en la Tabla 1 para calcular entalpías de reacción, muestran que la reacción en eq 4 es más exotérmica que la de la eq 5. Si se obedece la relación Evans-Polanyi, la primera reacción (eq 4) debería tener una energía de activación menor que la segunda (eq 5), pero parece ser cierto lo contrario. Las constantes de velocidad para estas reacciones, cuando se relacionan con las energías de activación a través de la ecuación de Arrhenius (eq 6), muestran que, a menos que los factores de frecuencia para estas dos reacciones sean bastante diferentes, la reacción dada en la ecuación 4 en realidad tiene una mayor energía de activación. Claramente, algo además de las entalpías de reacción debe tener un papel significativo en la determinación de las energías de activación para estas dos reacciones.

(4) .png

(5) .png

(6) .png

La identificación de un candidato probable para este factor adicional se puede hacer volviendo a las reacciones que se muestran en las ecuaciones 2 y 3 y recordando que estas reacciones muestran que algunos radicales centrados en carbono son nucleófilos y otros electrófilos. Si se asume que el radical terc- butilo es similar en su filicidad al radical ciclohexilo nucleófilo, entonces en la reacción en la ecuación 5 hay una coincidencia de polaridad entre el radical nucleófilo y el átomo de hidrógeno deficiente en electrones que se está abstrayendo. Dado que no existe una coincidencia similar en la reacción más lenta (eq 4), la filicidad radical se convierte en un candidato principal para el factor que se une con la entalpía de reacción al explicar las constantes de velocidad para las reacciones de abstracción de hidrógeno.