10.2: Método de Corriente de Rama

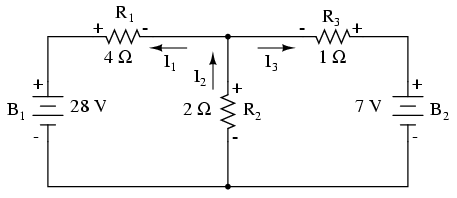
Usemos este circuito para ilustrar el método:

El primer paso es elegir un nodo (unión de cables) en el circuito para utilizarlo como punto de referencia para nuestras corrientes desconocidas. Voy a elegir el nodo que une la derecha de R ₁, la parte superior de R ₂ y la izquierda de R ₃.

En este nodo, adivina qué direcciones toman las corrientes de los tres cables, etiquetando las tres corrientes como I ₁, I ₂ y I ₃, respectivamente. Hay que tener en cuenta que estas direcciones de corriente son especulativas en este punto. Afortunadamente, si resulta que alguna de nuestras conjeturas estuvo equivocada, sabremos cuándo resolvemos matemáticamente para las corrientes (cualquier dirección actual “incorrecta” se mostrará como números negativos en nuestra solución).

La Ley Actual de Kirchhoff (KCL) nos dice que la suma algebraica de corrientes que entran y salen de un nodo debe ser igual a cero, así podemos relacionar estas tres corrientes (I ₁, I ₂ y I ₃) entre sí en una sola ecuación. Por el bien de la convención, denotaré cualquier corriente que ingrese al nodo como signo positivo, y cualquier corriente que salga del nodo como signo negativo:

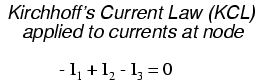
El siguiente paso es etiquetar todas las polaridades de caída de voltaje a través de las resistencias de acuerdo con las direcciones asumidas de las corrientes. Recuerde que el extremo “aguas arriba” de una resistencia siempre será negativo, y el extremo “aguas abajo” de una resistencia positivo uno con respecto al otro, ya que los electrones están cargados negativamente:

Las polaridades de las baterías, por supuesto, permanecen como estaban de acuerdo a su simbología (extremo corto negativo, extremo largo positivo). Está bien si la polaridad de la caída de voltaje de una resistencia no coincide con la polaridad de la batería más cercana, siempre y cuando la polaridad del voltaje de la resistencia se base correctamente en la dirección asumida de la corriente a través de ella. En algunos casos podemos descubrir que la corriente será forzada hacia atrás a través de una batería, provocando este mismo efecto. Lo importante a recordar aquí es basar todas sus polaridades de resistencia y cálculos posteriores en las direcciones de la (s) corriente (s) inicialmente asumida (s). Como se indicó anteriormente, si su suposición resulta ser incorrecta, será evidente una vez que las ecuaciones hayan sido resueltas (por medio de una solución negativa). La magnitud de la solución, sin embargo, seguirá siendo correcta.

La Ley de Voltaje (KVL) de Kirchhoff nos dice que la suma algebraica de todos los voltajes en un bucle debe ser igual a cero, así podemos crear más ecuaciones con términos actuales (I ₁, I ₂ y I ₃) para nuestras ecuaciones simultáneas. Para obtener una ecuación KVL, debemos contar las caídas de voltaje en un bucle del circuito, como si estuviéramos midiendo con un voltímetro real. Voy a elegir trazar primero el bucle izquierdo de este circuito, comenzando desde la esquina superior izquierda y moviéndome en sentido antihorario (la elección de puntos de partida y direcciones es arbitraria). El resultado se verá así:

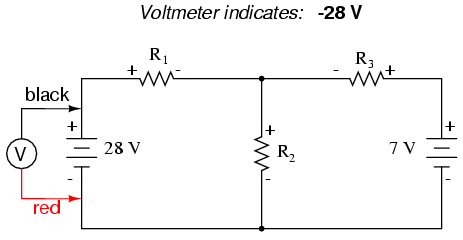
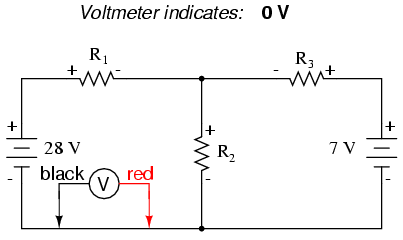
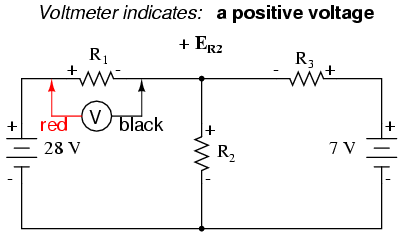
Habiendo completado nuestro rastro del bucle izquierdo, sumamos estas indicaciones de voltaje juntas para una suma de cero:

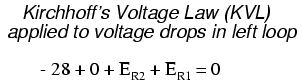
Por supuesto, aún no sabemos cuál es el voltaje a través de _R1 o _R2, por lo que no podemos insertar esos valores en la ecuación como cifras numéricas en este punto. No obstante, sí sabemos que los tres voltajes deben sumar algebraicamente a cero, por lo que la ecuación es cierta. Podemos ir un paso más allá y expresar los voltajes desconocidos como producto de las corrientes desconocidas correspondientes (I ₁ y I ₂) y sus respectivas resistencias, siguiendo la Ley de Ohm (E=IR), así como eliminar el término 0:

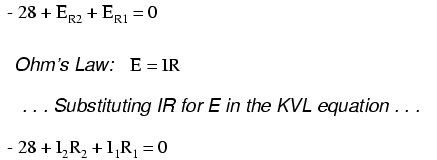
Como sabemos cuáles son los valores de todas las resistencias en ohmios, solo podemos sustituir esas figuras en la ecuación para simplificar un poco las cosas:

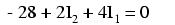
Quizás se esté preguntando por qué pasamos por toda la molestia de manipular esta ecuación desde su forma inicial (-28 + E _R2 + E _R1). Después de todo, los dos últimos términos aún se desconocen, entonces, ¿qué ventaja tiene expresarlos en términos de voltajes desconocidos o como corrientes desconocidas (multiplicadas por resistencias)? El propósito de hacer esto es obtener la ecuación KVL expresada usando las mismas variables desconocidas que la ecuación KCL, ya que esto es un requisito necesario para cualquier método de solución de ecuaciones simultáneas. Para resolver por tres corrientes desconocidas (I ₁, I ₂ y I ₃), debemos tener tres ecuaciones que relacionen estas tres corrientes (¡no voltajes!) juntos.

Aplicando los mismos pasos al bucle derecho del circuito (comenzando en el nodo elegido y moviéndose en sentido antihorario), obtenemos otra ecuación KVL:

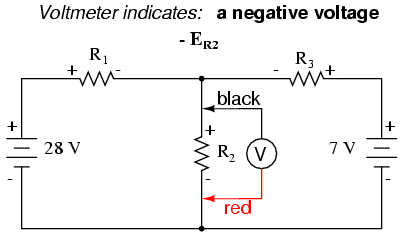
Sabiendo ahora que el voltaje a través de cada resistor puede ser y debe expresarse como el producto de la corriente correspondiente y la resistencia (conocida) de cada resistor, podemos reescribir la ecuación como tal:

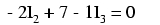
Ahora tenemos un sistema matemático de tres ecuaciones (una ecuación KCL y dos ecuaciones KVL) y tres incógnitas:

Para algunos métodos de solución (especialmente cualquier método que involucre una calculadora), es útil expresar cada término desconocido en cada ecuación, con cualquier valor constante a la derecha del signo igual, y con cualquier término de “unidad” expresado con un coeficiente explícito de 1. Reescribiendo de nuevo las ecuaciones, tenemos:

Usando cualquier técnica de solución disponible para nosotros, debemos llegar a una solución para los tres valores actuales desconocidos:

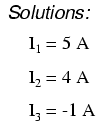
Entonces, I ₁ es 5 amperios, I ₂ es 4 amperios, y I ₃ es un negativo 1 amp. Pero, ¿qué significa corriente “negativa”? En este caso, significa que nuestra dirección asumida para I ₃ era opuesta a su dirección real. Volviendo a nuestro circuito original, podemos volver a dibujar la flecha de corriente para I ₃ (y volver a dibujar la polaridad de la caída de voltaje de R ₃ para que coincida):

¡Observe cómo la corriente se empuja hacia atrás a través de la batería 2 (electrones fluyendo “hacia arriba”) debido al mayor voltaje de la batería 1 (cuya corriente apunta “hacia abajo” como lo haría normalmente)! A pesar de que la polaridad de la batería _B2 está tratando de empujar electrones hacia abajo en esa rama del circuito, los electrones están siendo forzados hacia atrás a través de él debido al voltaje superior de la batería B ₁. ¿Significa esto que la batería más fuerte siempre “ganará” y la batería más débil siempre obtendrá corriente forzada a través de ella hacia atrás? ¡No! En realidad, depende tanto de los voltajes relativos de las baterías como de los valores de resistencia en el circuito. La única manera segura de determinar lo que está pasando es tomarse el tiempo para analizar matemáticamente la red.

Ahora que conocemos la magnitud de todas las corrientes en este circuito, podemos calcular las caídas de voltaje en todas las resistencias con la Ley de Ohm (E=IR):

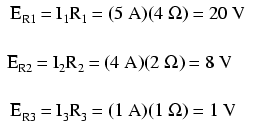
Analicemos ahora esta red usando SPICE para verificar nuestras cifras de voltaje. Podríamos analizar la corriente también con SPICE, pero como eso requiere la inserción de componentes adicionales en el circuito, y porque sabemos que si los voltajes son todos iguales y todas las resistencias son iguales, las corrientes deben ser todas iguales, optaré por el análisis menos complejo. Aquí hay un re-dibujo de nuestro circuito, completo con números de nodo para SPICE como referencia:

Efectivamente, todas las cifras de voltaje resultan ser las mismas: 20 voltios a través de R ₁ (nodos 1 y 2), 8 voltios a través de R ₂ (nodos 2 y 0), y 1 voltio a través de R ₃ (nodos 2 y 3). Toma nota de las señales de todas estas cifras de voltaje: ¡todas son valores positivos! SPICE basa sus polaridades en el orden en que se listan los nodos, siendo el primer nodo positivo y el segundo nodo negativo. Por ejemplo, una cifra de positivo (+) 20 voltios entre los nodos 1 y 2 significa que el nodo 1 es positivo con respecto al nodo 2. Si la cifra hubiera salido negativa en el análisis SPICE, habríamos sabido que nuestra polaridad real era “hacia atrás” (nodo 1 negativo con respecto al nodo 2). Al verificar las órdenes de los nodos en el listado SPICE, podemos ver que todas las polaridades coinciden con lo que determinamos a través del método de análisis de Corriente Rama.

Revisar

• Pasos a seguir para el método de análisis “Branch Current”:

(1) Elija un nodo y asuma direcciones de corrientes.

(2) Escribir una ecuación KCL relacionando las corrientes en el nodo.

(3) Etiquete polaridades de caída de voltaje de resistencia basadas en corrientes asumidas.

(4) Escribir ecuaciones KVL para cada bucle del circuito, sustituyendo el producto IR por E en cada término de resistencia de las ecuaciones.

(5) Resolver corrientes de rama desconocidas (ecuaciones simultáneas).

(6) Si alguna solución es negativa, ¡entonces la dirección supuesta de la corriente para esa solución es incorrecta!

(7) Resuelve caídas de voltaje en todas las resistencias (E=IR).