10.3: Método y Análisis de Corriente de Malla

Corriente de malla, método convencional

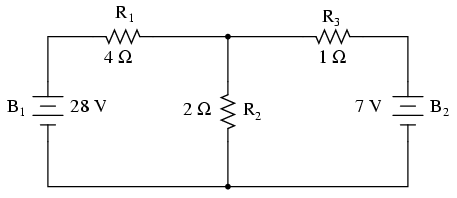
Veamos cómo funciona este método en el mismo problema de ejemplo:

Identificación de bucles en un circuito

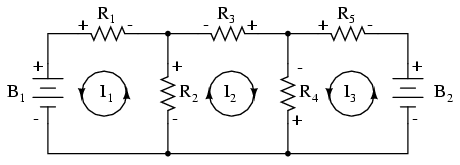
El primer paso en el método Mesh Current es identificar “bucles” dentro del circuito que abarcan todos los componentes. En nuestro circuito de ejemplo, el bucle formado por B ₁, R1 y _R2 será el primero mientras que el bucle formado por B ₂, R2 y R ₃ será el segundo. La parte más extraña del método Mesh Current es imaginar corrientes circulantes en cada uno de los bucles. De hecho, este método recibe su nombre de la idea de que estas corrientes engranan entre bucles como conjuntos de engranajes giratorios:

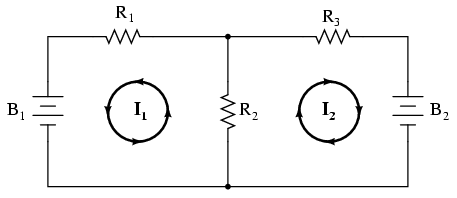
La elección de la dirección de cada corriente es totalmente arbitraria, al igual que en el método de Corriente Rama, pero las ecuaciones resultantes son más fáciles de resolver si las corrientes van en la misma dirección a través de componentes que se cruzan (observe cómo las corrientes I ₁ y I ₂ van “arriba” a través de resistencia R ₂, donde se “mallan” o se cruzan). Si la dirección asumida de una corriente de malla es incorrecta, la respuesta para esa corriente tendrá un valor negativo.

Etiquetar las polaridades de caída de voltaje

El siguiente paso es etiquetar todas las polaridades de caída de voltaje a través de las resistencias de acuerdo con las direcciones asumidas de las corrientes de malla. Recuerde que el extremo “aguas arriba” de una resistencia siempre será negativo, y el extremo “aguas abajo” de una resistencia positivo uno con respecto al otro, ya que los electrones están cargados negativamente. Las polaridades de la batería, por supuesto, están dictadas por sus orientaciones de símbolo en el diagrama, y pueden o no “estar de acuerdo” con las polaridades de la resistencia (direcciones de corriente asumidas):

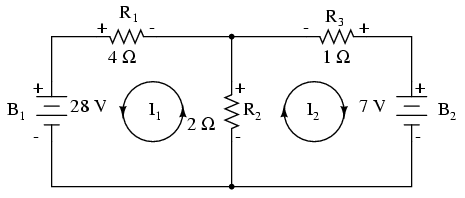
Usando la Ley de Voltaje de Kirchhoff, ahora podemos dar un paso alrededor de cada uno de estos bucles, generando ecuaciones representativas de las caídas de voltaje y polaridades de los componentes. Al igual que con el método de Corriente de Rama, denotaremos una caída de voltaje de una resistencia como el producto de la resistencia (en ohmios) y su respectiva corriente de malla (siendo desconocida esa cantidad en este punto). Donde dos corrientes engranan juntas, escribiremos ese término en la ecuación con la corriente de resistencia siendo la suma de las dos corrientes de malla.

Rastreo del Bucle Izquierdo del Circuito con Ecuaciones

Rastreando el bucle izquierdo del circuito, comenzando desde la esquina superior izquierda y moviéndose en sentido antihorario (la elección de los puntos de partida y direcciones es finalmente irrelevante), contando la polaridad como si tuviéramos un voltímetro en la mano, plomo rojo en el punto adelante y plomo negro en el punto de atrás, obtenemos esta ecuación:

Observe que el término medio de la ecuación utiliza la suma de las corrientes de malla I ₁ e I ₂ como la corriente a través de la resistencia _R2. Esto se debe a que las corrientes de malla I ₁ e I ₂ van en la misma dirección a través de R ₂, y así se complementan entre sí. Distribuyendo el coeficiente de 2 a los términos I ₁ e I ₂, y luego combinando I ₁ términos en la ecuación, podemos simplificar como tal:

En este momento tenemos una ecuación con dos incógnitas. Para poder resolver dos corrientes de malla desconocidas, debemos tener dos ecuaciones. Si trazamos el otro bucle del circuito, podemos obtener otra ecuación KVL y tener datos suficientes para resolver para las dos corrientes. Criatura de hábito que soy, comenzaré en la esquina superior izquierda del bucle derecho y trazaré en sentido antihorario:

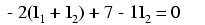
Simplificando la ecuación como antes, terminamos con:

Ahora, con dos ecuaciones, podemos usar uno de varios métodos para resolver matemáticamente para las corrientes desconocidas I ₁ y I ₂:

Sabiendo que estas soluciones son valores para corrientes de malla, no corrientes de ramificación, debemos volver a nuestro diagrama para ver cómo encajan entre sí para dar corrientes a través de todos los componentes:

La solución de -1 amp para I ₂ significa que nuestra dirección inicialmente asumida de la corriente era incorrecta. En la actualidad, I ₂ fluye en sentido contrario a las agujas del reloj a un valor de (positivo) 1 amperio:

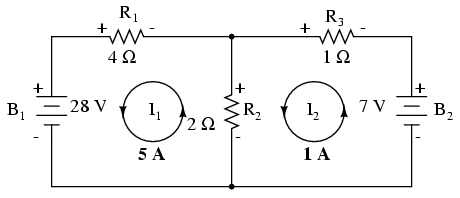
Este cambio de dirección de la corriente a partir de lo que se asumió primero alterará la polaridad de las caídas de voltaje a través de R ₂ y R ₃ debido a la corriente _I2. _{A partir de aquí, podemos decir que la corriente a través de R1 es de 5 amperios, siendo la caída de voltaje a través de R1 el producto de corriente y resistencia (E=IR), 20 voltios (positivo a la izquierda y negativo a la derecha).} También, podemos decir con seguridad que la corriente a través de R ₃ es de 1 amperio, con una caída de voltaje de 1 voltio (E=IR), positiva a la izquierda y negativa a la derecha. Pero, ¿qué está pasando en la R ₂?

La corriente de malla I ₁ va “arriba” a través de R ₂, mientras que la corriente de malla I ₂ va “hacia abajo” a través de R ₂. Para determinar la corriente real a través de R ₂, debemos ver cómo interactúan las corrientes de malla I ₁ e I ₂ (en este caso están en oposición), y agregarlas algebraicamente para llegar a un valor final. Como I ₁ va “arriba” a 5 amperios, y I ₂ va “abajo” en 1 amp, la corriente real a través de R ₂ debe ser un valor de 4 amperios, yendo “arriba:”

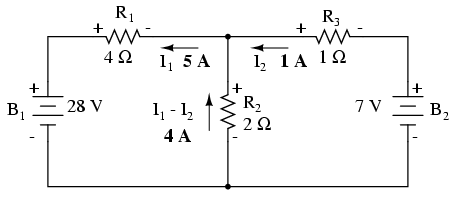
_{Una corriente de 4 amperios a través de la resistencia de 2 Ω de R 2 nos da una caída de voltaje de 8 voltios (E=IR), positiva en la parte superior y negativa en la parte inferior.}

Ventaja del análisis de corriente de malla

La principal ventaja del análisis Mesh Current es que generalmente permite la solución de una gran red con menos valores desconocidos y menos ecuaciones simultáneas. Nuestro problema de ejemplo tomó tres ecuaciones para resolver el método de Corriente de Rama y solo dos ecuaciones usando el método Mesh Current. Esta ventaja es mucho mayor a medida que las redes aumentan en complejidad:

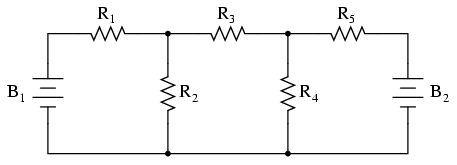
Para resolver esta red usando Corrientes de Sucursal, tendríamos que establecer cinco variables para dar cuenta de todas y cada una de las corrientes únicas en el circuito (I ₁ a I ₅). Esto requeriría cinco ecuaciones para su solución, en forma de dos ecuaciones KCL y tres ecuaciones KVL (dos ecuaciones para KCL en los nodos y tres ecuaciones para KVL en cada bucle):

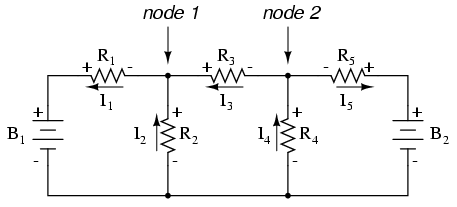
Supongo que si no tienes nada mejor que ver con tu tiempo que resolver para cinco variables desconocidas con cinco ecuaciones, quizás no te moleste usar el método de análisis de Corriente Rama para este circuito. Para aquellos de nosotros que tenemos mejores cosas que hacer con nuestro tiempo, el método Mesh Current es mucho más fácil, requiriendo solo tres incógnitas y tres ecuaciones para resolver:

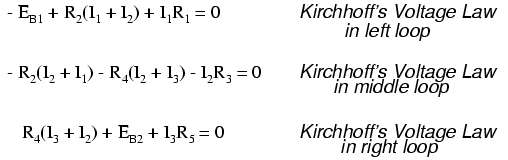
Menos ecuaciones con las que trabajar es una ventaja decidida, especialmente cuando se realiza una solución de ecuaciones simultáneas a mano (sin calculadora).

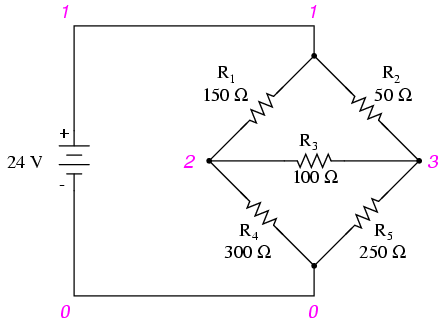
Otro tipo de circuito que se presta bien a Mesh Current es el desequilibrado Wheatstone Bridge. Tomemos este circuito, por ejemplo:

Dado que las relaciones de R ₁ /R ₄ y R ₂ /R ₅ son desiguales, sabemos que habrá voltaje a través de la resistencia R ₃, y cierta cantidad de corriente a través de ella. Como se discutió al inicio de este capítulo, este tipo de circuito es irreducible por análisis serie-paralelo normal, y sólo puede ser analizado por algún otro método.

Podríamos aplicar el método de Corriente Rama a este circuito, pero requeriría seis corrientes (I ₁ a I ₆), lo que llevaría a un conjunto muy grande de ecuaciones simultáneas para resolver. Sin embargo, usando el método Mesh Current, podemos resolver todas las corrientes y voltajes con muchas menos variables.

El primer paso en el método Mesh Current es dibujar las corrientes de malla suficientes para dar cuenta de todos los componentes del circuito. Mirando nuestro circuito de puentes, debería ser obvio dónde colocar dos de estas corrientes:

Las direcciones de estas corrientes de malla, por supuesto, son arbitrarias. No obstante, dos corrientes de malla no son suficientes en este circuito, porque ni I ₁ ni I ₂ pasan por la batería. Entonces, debemos agregar una tercera corriente de malla, I ₃:

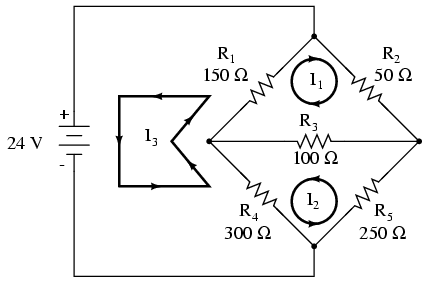
Aquí, he elegido I ₃ para hacer un bucle desde el lado inferior de la batería, pasando por R ₄, pasando por R ₁, y de vuelta al lado superior de la batería. Este no es el único camino que podría haber elegido para I ₃, sino que parece el más simple.

Ahora, debemos etiquetar las polaridades de caída de voltaje de la resistencia, siguiendo cada una de las direcciones de las corrientes asumidas:

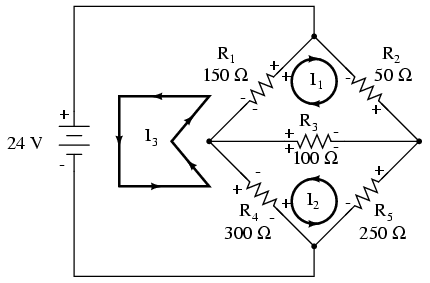
Observe algo muy importante aquí: en la resistencia R ₄, las polaridades para las respectivas corrientes de malla no coinciden. Esto se debe a que esas corrientes de malla (I ₂ e I ₃) están pasando por R ₄ en diferentes direcciones. Esto no excluye el uso del método de análisis Mesh Current, pero sí lo complica un poco. Aunque más adelante, mostraremos cómo evitar el choque actual de R ₄. (Ver ejemplo a continuación)

Generar una ecuación KVL para el bucle superior del puente, comenzando desde el nodo superior y trazando en sentido horario:

En esta ecuación, representamos las direcciones comunes de las corrientes por sus sumas a través de resistencias comunes. Por ejemplo, la resistencia R ₃, con un valor de 100 Ω, tiene su caída de voltaje representada en la ecuación KVL anterior por la expresión 100 (I ₁ + I ₂), ya que ambas corrientes I ₁ y I ₂ pasan por R ₃ de derecha a izquierda. _{Lo mismo puede decirse de la resistencia R1, con su expresión de caída de voltaje mostrada como 150 (I 1 + I 3), ya que tanto I 1 como I 3 van de abajo hacia arriba a través de esa resistencia, y así trabajan juntos para generar su caída de voltaje.}

Generar una ecuación KVL para el bucle inferior del puente no será tan fácil, ya que tenemos dos corrientes yendo una contra la otra a través de la resistencia R ₄. Así es como lo hago (comenzando en el nodo de la derecha, y trazando en sentido antihorario):

Observe cómo el segundo término en la forma original de la ecuación tiene el valor de la resistencia R ₄ de 300 Ω multiplicado por la diferencia entre I ₂ y I ₃ (I ₂ - I ₃). Es así como representamos el efecto combinado de dos corrientes de malla que van en direcciones opuestas a través del mismo componente. Elegir los signos matemáticos apropiados es muy importante aquí: 300 (I ₂ - I ₃) no significa lo mismo que 300 (I ₃ - I ₂). Elegí escribir 300 (I ₂ - I ₃) porque estaba pensando primero en el efecto de I ₂ (creando una caída de voltaje positiva, midiendo con un voltímetro imaginario a través de R ₄, plomo rojo en la parte inferior y plomo negro en la parte superior), y secundariamente en el efecto de I ₃ (creando una caída de voltaje negativa, un cable rojo en la parte inferior y un cable negro en la parte superior). Si hubiera pensado primero en términos del efecto de I ₃ y el efecto de I ₂ secundariamente, sosteniendo mis derivaciones imaginarias del voltímetro en las mismas posiciones (rojo en la parte inferior y negro en la parte superior), la expresión habría sido -300 (I ₃ - I ₂). Obsérvese que esta expresión es matemáticamente equivalente a la primera: +300 (I ₂ - I ₃).

Bueno, eso se encarga de dos ecuaciones, pero todavía necesito una tercera ecuación para completar mi conjunto de ecuaciones simultáneas de tres variables, tres ecuaciones. Esta tercera ecuación también debe incluir el voltaje de la batería, que hasta este punto no aparece en ninguna de las dos ecuaciones KVL anteriores. Para generar esta ecuación, volveré a trazar un bucle con mi voltímetro imaginario comenzando desde el terminal inferior (negativo) de la batería, escalando en sentido horario (nuevamente, la dirección en la que paso es arbitraria, y no necesita ser la misma que la dirección de la corriente de malla en ese bucle):

Resolviendo para I ₁, I ₂ y I ₃ usando cualquier método de ecuación simultánea que preferimos:

Ejemplo:

Use Octave para encontrar la solución para I ₁, I ₂ e I ₃ de la forma simplificada de ecuaciones anterior.

Solución:

En Octave, un clon Matlab® de código abierto, ingrese los coeficientes en la matriz A entre corchetes con elementos de columna separados por comas, y filas de punto y coma separados.Introduzca los voltajes en el vector de columna: b. Las corrientes desconocidas: I ₁, ₂, y I ₃ se calculan por el comando: x=A\ b. Estos están contenidos dentro del vector de columna x.

El valor negativo al que llegó para I ₁ nos dice que la dirección asumida para esa corriente de malla era incorrecta. Por lo tanto, los valores de corriente reales a través de cada resistencia son como tales:

Cálculo de caídas de voltaje en cada resistor:

Una simulación SPICE confirma la precisión de nuestros cálculos de voltaje:

Ejemplo:

(a) Encontrar una nueva ruta para la corriente I ₃ que no produzca una polaridad conflictiva en ninguna resistencia en comparación con I ₁ o I ₂. R ₄ fue el componente infractor. b) Encontrar valores para I ₁, I ₂ y I ₃. (c) Encuentre las cinco corrientes de resistencia y compárelas con los valores anteriores.

Solución:

(a) Ruta I ₃ a través de R ₅, R ₃ y R ₁ como se muestra:

Tenga en cuenta que se ha eliminado la polaridad conflictiva en R ₄. Además, ninguna de las otras resistencias tiene polaridades contradictorias.

(b) Octave, un clon matlab de código abierto (libre), produce un vector de corriente de malla en “x”:

No todas las corrientes I ₁, I ₂ e I ₃ son las mismas (I ₂) que el puente anterior debido a diferentes trayectorias de bucle Sin embargo, las corrientes de resistencia se comparan con los valores anteriores:

Dado que las corrientes de resistencia son las mismas que los valores anteriores, los voltajes de la resistencia serán idénticos y no es necesario volver a calcularlos.

Revisar

• Pasos a seguir para el método de análisis “Mesh Current”:

(1) Dibuje corrientes de malla en bucles de circuito, suficientes para dar cuenta de todos los componentes.

(2) Etiquete polaridades de caída de voltaje de resistencia basadas en direcciones asumidas de corrientes de malla.

(3) Escribir ecuaciones KVL para cada bucle del circuito, sustituyendo el producto IR por E en cada término de resistencia de la ecuación. Donde dos corrientes de malla se cruzan a través de un componente, expresan la corriente como la suma algebraica de esas dos corrientes de malla (es decir, I ₁ + I ₂) si las corrientes van en la misma dirección a través de ese componente. De no ser así, expresar la corriente como la diferencia (es decir, I ₁ - I ₂).

(4) Resolver corrientes de malla desconocidas (ecuaciones simultáneas).

(5) Si alguna solución es negativa, ¡entonces la dirección actual supuesta es incorrecta!

(6) Algebraicamente agregar corrientes de malla para encontrar corriente en componentes que comparten múltiples corrientes de malla.

(7) Resuelve caídas de voltaje en todas las resistencias (E=IR).

Corriente de malla por inspección

Echamos un segundo vistazo al “método de corriente de malla” con todas las corrientes funcionando en sentido antihorario (ccw). La motivación es simplificar la escritura de ecuaciones de malla ignorando la polaridad de caída de voltaje de la resistencia. Sin embargo, debemos prestar atención a la polaridad de las fuentes de voltaje con respecto a la dirección de corriente asumida. El signo de las caídas de voltaje de la resistencia seguirá un patrón fijo.

Si escribimos un conjunto de ecuaciones convencionales de corriente de malla para el circuito de abajo, donde sí prestamos atención a los signos de la caída de voltaje a través de las resistencias, podemos reorganizar los coeficientes en un patrón fijo:

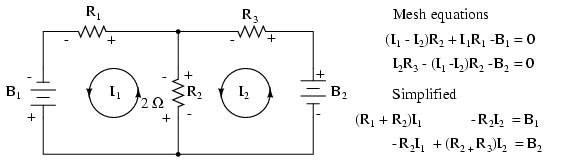
Una vez reordenados, podemos escribir ecuaciones por inspección. Los signos de los coeficientes siguen un patrón fijo en el par anterior, o el conjunto de tres en las reglas a continuación.

Reglas actuales de malla:

Este método asume fuentes de voltaje de flujo de electrones (no flujo de corriente convencional). Reemplace cualquier fuente de corriente en paralelo con una resistencia con una fuente de voltaje equivalente en serie con una resistencia equivalente.

Ignorando la dirección de la corriente o la polaridad de voltaje en las resistencias, dibuje bucles de corriente en sentido antihorario que atraviesan todos los Evite los bucles anidados.

Escribir ecuaciones de ley de voltaje en términos de corrientes desconocidas: I ₁, I ₂ y I ₃. La ecuación 1, el coeficiente 1, la ecuación 2, el coeficiente 2 y el coeficiente 3 de la ecuación 3 son las sumas positivas de resistencias alrededor de los bucles respectivos.

Todos los demás coeficientes son negativos, representativos de la resistencia común a un par de bucles. Ecuación 1 coeficiente 2 es la resistencia común a los bucles 1 y 2, coeficiente 3 la resistencia común a los bucles 1 y 3. Repita para otras ecuaciones y coeficientes.

El lado derecho de las ecuaciones es igual a cualquier fuente de voltaje de flujo de corriente electrónica. Un aumento de voltaje con respecto a la corriente supuesta en sentido contrario a las agujas del reloj es positiva, y 0 para ninguna fuente de voltaje.

Resolver ecuaciones para corrientes de malla:I ₁, I ₂ y I ₃. Resuelve corrientes a través de resistencias individuales con KCL. Resuelve tensiones con Ley de Ohmios y KVL.

Si bien las reglas anteriores son específicas para un circuito de tres mallas, las reglas pueden extenderse a mallas más pequeñas o más grandes. La siguiente figura ilustra la aplicación de las reglas. Las tres corrientes son todas dibujadas en la misma dirección, en sentido antihorario. Se escribe una ecuación KVL para cada uno de los tres bucles. Tenga en cuenta que no hay polaridad dibujada en las resistencias. No lo necesitamos para determinar los signos de los coeficientes. Aunque sí necesitamos prestar atención a la polaridad de la fuente de voltaje con respecto a la dirección de la corriente. La corriente I ₃ en sentido antihorario atraviesa la fuente de 24V de (+) a (-). Esto es un aumento de voltaje para el flujo de corriente de electrones. Por lo tanto, la tercera ecuación del lado derecho es +24V.

En Octava, ingresa los coeficientes en la matriz A con elementos de columna separados por comas y filas separadas por punto y coma. Ingresa los voltajes en el vector de columna b. Resuelve para las corrientes desconocidas: I ₁, I ₂ y I ₃ con el comando: x=A\ b. Estas corrientes están contenidas dentro del vector de columna x. Los valores positivos indican que las tres corrientes de malla fluyen todas en el supuesto sentido contrario a las agujas del reloj.

Las corrientes de malla coinciden con la solución anterior mediante un método de corriente de malla diferente. El cálculo de tensiones y corrientes de resistencia será idéntico a la solución anterior. No hace falta repetir aquí.

Tenga en cuenta que los textos de ingeniería eléctrica se basan en el flujo de corriente convencional. El método de corriente de bucle, corriente de malla en esos textos ejecutará las corrientes de malla asumidas en sentido horario. La corriente convencional fluye fuera del terminal (+) de la batería a través del circuito, volviendo al terminal (-). Un aumento de voltaje de corriente convencional corresponde a rastrear la corriente supuesta de (-) a (+) a través de cualquier fuente de voltaje.

Sigue un ejemplo más de un circuito anterior. La resistencia alrededor del bucle 1 es de 6 Ω, alrededor del bucle 2:3 Ω. La resistencia común a ambos bucles es de 2 Ω. Obsérvese los coeficientes de I ₁ e I ₂ en el par de ecuaciones. Rastrear la supuesta corriente del bucle 1 en sentido antihorario a través de B ₁ de (+) a (-) corresponde a un aumento de voltaje de flujo de corriente electrónica. Así, el signo de los 28 V es positivo. El bucle 2 en sentido antihorario asumió trazas de corriente (-) a (+) a través de B ₂, una caída de voltaje. Así, el signo de B ₂ es negativo, -7 en la ecuación de la 2ª malla. Una vez más, no hay marcas de polaridad en las resistencias. Tampoco figuran en las ecuaciones.

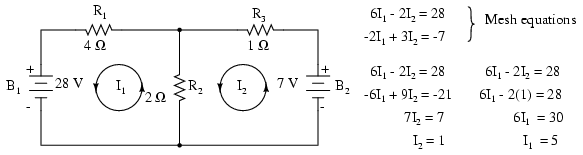
Las corrientes I ₁ = 5 A, e I ₂ = 1 A son ambas positivas. Ambos fluyen en la dirección de los bucles en sentido contrario a las agujas del reloj. Esto se compara con los resultados anteriores.

Resumen:

• El método de corriente de malla modificada evita tener que determinar los signos de los coeficientes de ecuación dibujando todas las corrientes de malla en sentido antihorario para el flujo de corriente electrónica.
• Sin embargo, sí necesitamos determinar el signo de cualquier fuente de voltaje en el bucle. La fuente de voltaje es positiva si la corriente ccw supuesta fluye con la batería (fuente). El signo es negativo si la corriente ccw supuesta fluye contra la batería.
• Consulte las reglas anteriores para obtener más detalles.