2.5: Razonamiento inductivo a partir de patrones
- Page ID
- 107382
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Razonamiento Inductivo
Un tipo de razonamiento es el razonamiento inductivo. El razonamiento inductivo implica sacar conclusiones basadas en ejemplos y patrones. Los patrones visuales y los patrones numéricos proporcionan buenos ejemplos de razonamiento inductivo. Veamos algunos patrones para tener una idea de lo que es el razonamiento inductivo.
¿Y si te dieran un patrón de tres números o formas y te pidieran determinar el sexto número o forma que se ajustara a ese patrón?
Ejemplo\(\PageIndex{1}\)
A continuación se muestra un patrón de puntos. ¿Cuántos puntos habría en la\(4^{th}\) figura? ¿Cuántos puntos habría en la\(6^{th}\) figura?
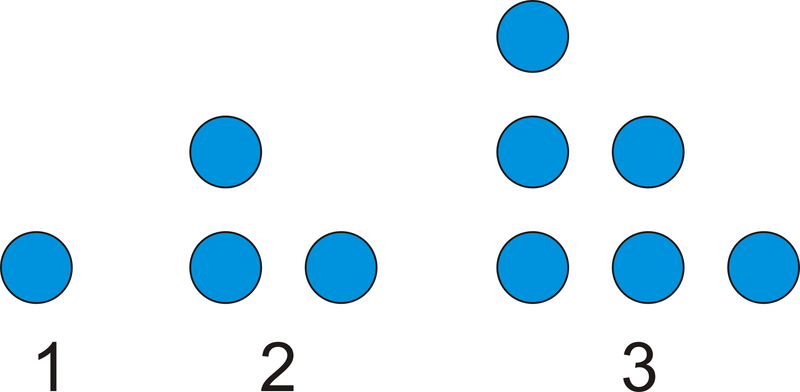Figura\(\PageIndex{1}\)Solución
Dibuja un cuadro. Contando los puntos, hay\(4+3+2+1=10\) puntos.
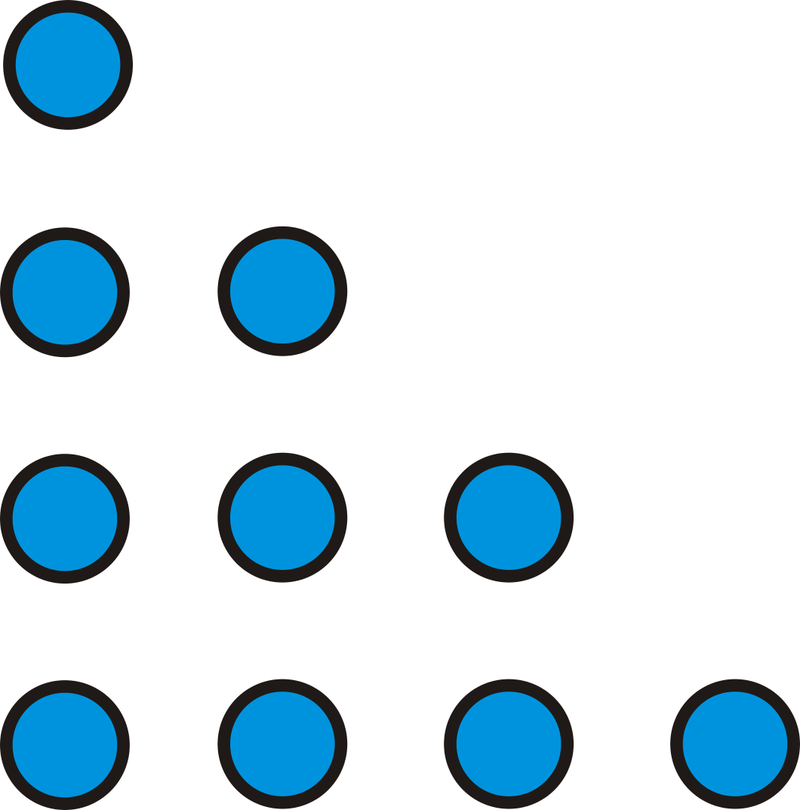Figura\(\PageIndex{2}\)Para la\(6^{th}\) figura, podemos usar el mismo patrón,\(6+5+4+3+2+1\). Hay 21 puntos en la\(6^{th}\) figura.
Ejemplo\(\PageIndex{2}\)
¿Cuántos triángulos habría en la\(10^{th}\) figura?
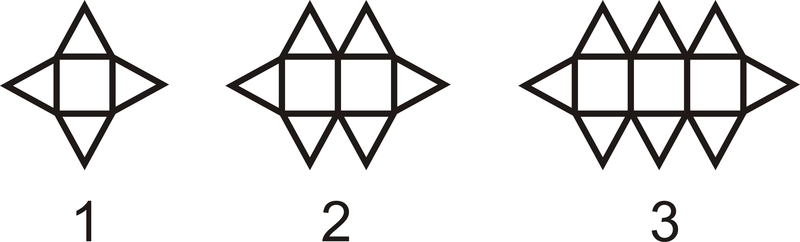Figura\(\PageIndex{3}\)Solución
Habría 10 cuadrados en la\(10^{th}\) figura, con un triángulo por encima y por debajo de cada uno. También hay un triángulo en cada extremo de la figura. Eso hace\(10+10+2=22\) triángulos en todos.
Ejemplo\(\PageIndex{3}\)
Mira el patrón\(2, 4, 6, 8, 10, \ldots\) ¿Cuál es el\(19^{th}\) término en el patrón?
Solución
Cada término es 2 más que el término anterior.
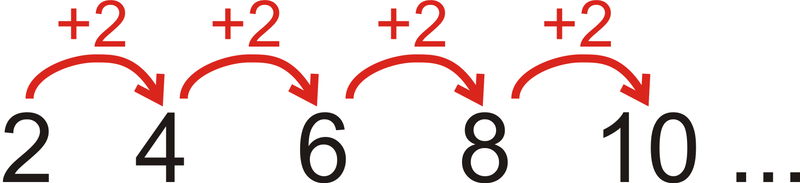Figura\(\PageIndex{4}\)Se podría contar el patrón hasta el\(19^{th}\) término, pero eso podría llevar un tiempo. Observe que el\(1^{st}\) término es\(2 \cdot 1\), el 2do término es\(2 \cdot 2\), el 3er término es\(2 \cdot 3\), y así sucesivamente. Entonces, el\(19^{th}\) término sería\(2 \cdot 19\) o 38.
Ejemplo\(\PageIndex{4}\)
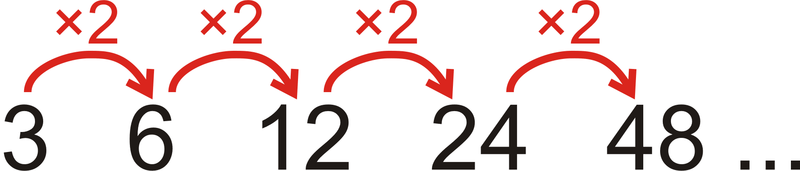
Mira el patrón:\(3, 6, 12, 24, 48, \ldots\)
¿Cuál es el siguiente término en el patrón? ¿Cuál es el\(10^{th}\) término?
Solución
Cada término se multiplica por 2 para obtener el siguiente término.
Figura\(\PageIndex{5}\)Por lo tanto, el siguiente término será\(48 \cdot 2\) o 96.
Para encontrar el\(10^{th}\) término, continuar multiplicando por 2, o\(3\cdot \underbrace{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2 \cdot 2 }_{2^{9}}=1536\).
Ejemplo\(\PageIndex{5}\)
Encuentra el octavo término en la lista de números:\(2, \dfrac{3}{4}, \dfrac{4}{9}, \dfrac{5}{16}, \dfrac{6}{25}\ldots\)
Solución
Primero, cambie 2 en una fracción, o\(\dfrac{2}{1}\). Entonces, el patrón es ahora\(\dfrac{2}{1}, \dfrac{3}{4}, \dfrac{4}{9}, \dfrac{5}{16}, \dfrac{6}{25}\ldots\) La parte superior es\(2, 3, 4, 5, 6\). Aumenta en 1 cada vez, por lo que el numerador del\(8^{th}\) término es 9. Los denominadores son los números cuadrados, por lo que el denominador del\(8^{th}\) término es\(8^2\) o 64. El\(8^{th}\) término es\(\dfrac{9}{64}\).
Revisar
Para las preguntas 1-3, determine cuántos puntos habría en el\(4^{th}\) y el\(10^{th}\) patrón de cada figura a continuación.
-
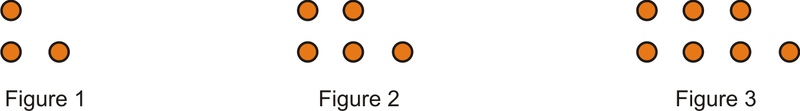Figura\(\PageIndex{6}\) -
Figura\(\PageIndex{7}\) -
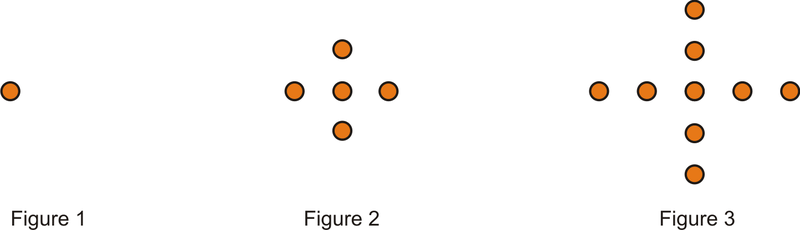Figura\(\PageIndex{8}\) - Utilice el patrón a continuación para responder a las preguntas.
Figura\(\PageIndex{9}\)- Dibuja la siguiente figura en el patrón.
- ¿Cómo se relaciona el número de puntos en cada estrella con el número de figura?
- Utilice el patrón a continuación para responder a las preguntas. Todos los triángulos son triángulos equiláteros.
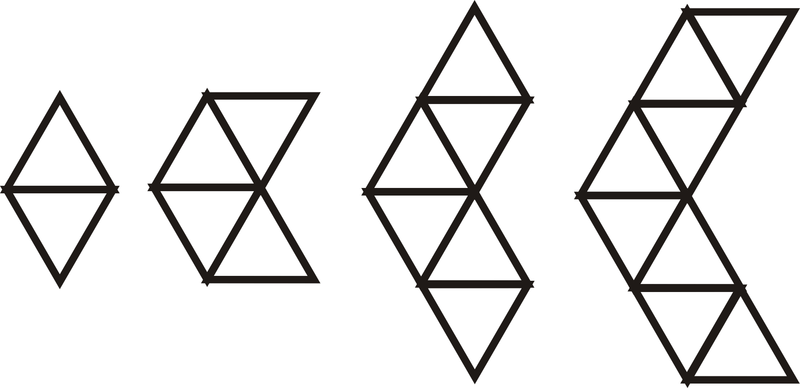Figura\(\PageIndex{10}\)- Dibuja la siguiente figura en el patrón. ¿Cuántos triángulos tiene?
- Determinar cuántos triángulos hay en la\(24^{th}\) figura.
Para las preguntas 6-13, determinar: los siguientes tres términos en el patrón.
- \(5, 8, 11, 14, 17, \ldots\)
- \(6, 1, -4, -9, -14, \ldots\)
- \(2, 4, 8, 16, 32, \ldots\)
- \(67, 56, 45, 34, 23, \ldots\)
- \(9, -4, 6, -8, 3, \ldots\)
- \(\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \ldots\)
- \(\dfrac{2}{3}, \dfrac{4}{7}, \dfrac{6}{11},\dfrac{8}{15}, \dfrac{10}{19},\ldots\)
- \(-1, 5, -9, 13, -17, \ldots\)
Para las preguntas 14-17, determinar los dos términos siguientes y describir el patrón.
- \(3, 6, 11, 18, 27, \ldots\)
- \(3, 8, 15, 24, 35, \ldots\)
- \(1, 8, 27, 64, 125, \ldots\)
- \(1, 1, 2, 3, 5, \ldots\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.1.
vocabulario
| Término | Definición |
|---|---|
| Razonamiento Inductivo | El razonamiento inductivo es un tipo de razonamiento en el que se extraen conclusiones de patrones y ejemplos previos. |
| Triángulo Equilátero | Un triángulo equilátero es un triángulo en el que los tres lados tienen la misma longitud. |
Recursos adicionales
Elemento Interactivo
Video: Razonamiento Inductivo
Actividades: Razonamiento inductivo a partir de patrones Preguntas de discusión
Ayudas de estudio: Guía de estudio de tipos de razonamiento
Práctica: Razonamiento inductivo a partir de patrones
Mundo real: La ciencia de la inducción