3.2: Líneas paralelas y sesgadas
- Page ID
- 107394
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Líneas que nunca se cruzan.
Las líneas paralelas son dos o más líneas que se encuentran en un mismo plano y nunca se cruzan. Para mostrar que las líneas son paralelas, se utilizan flechas.
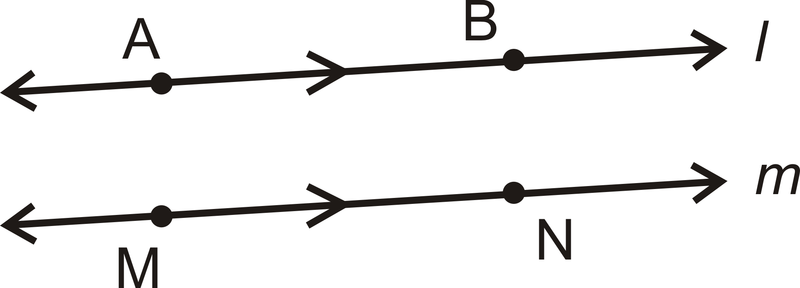
| Etiquetarlo | Dilo |
|---|---|
| \(\overleftrightarrow{AB} \parallel \overleftrightarrow{MN}\) | \(AB\)La línea es paralela a la línea\(MN\) |
| \(l\parallel m\) | \(l\)La línea es paralela a la línea\(m\). |
En la definición de paralelo se utiliza la palabra “línea”. Sin embargo, los segmentos de línea, los rayos y los planos también pueden ser paralelos. La siguiente imagen muestra dos planos paralelos, con un tercer plano azul que es perpendicular a ambos.
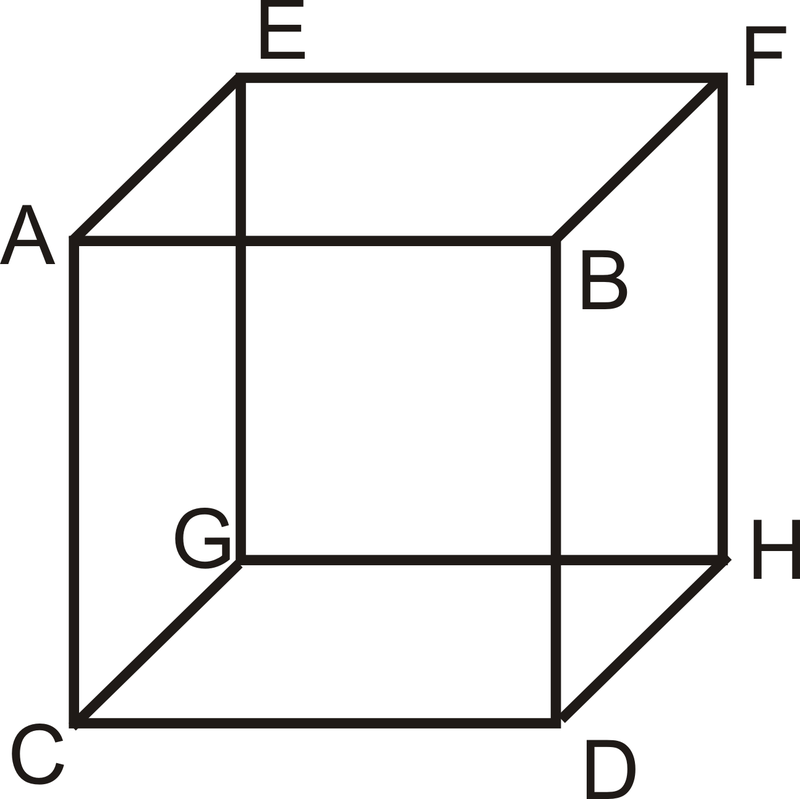
Las líneas sesgadas son líneas que están en diferentes planos y nunca se cruzan. Son diferentes de las líneas paralelas porque las líneas paralelas se encuentran en el MISMO plano. En el cubo de abajo,\(\overline{AB}\) y\(\overline{FH}\) son sesgadas\(\overline{AC}\) y y\(\overline{EF}\) sesgadas.
Datos básicos sobre las líneas paralelas
Propiedad: Si líneas\(l\parallel m\) y\(m\parallel n\), entonces\(l\parallel n\).
Si
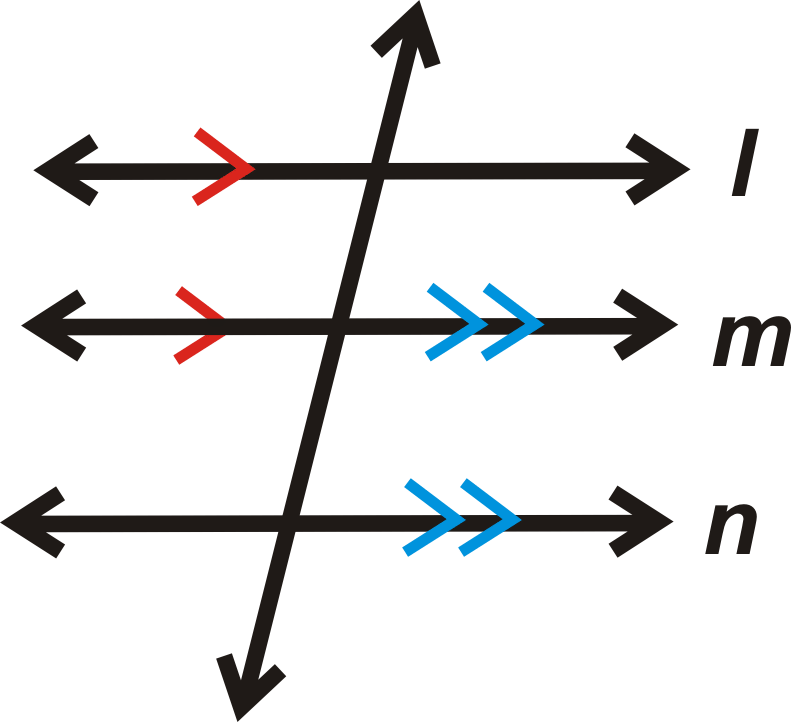
entonces
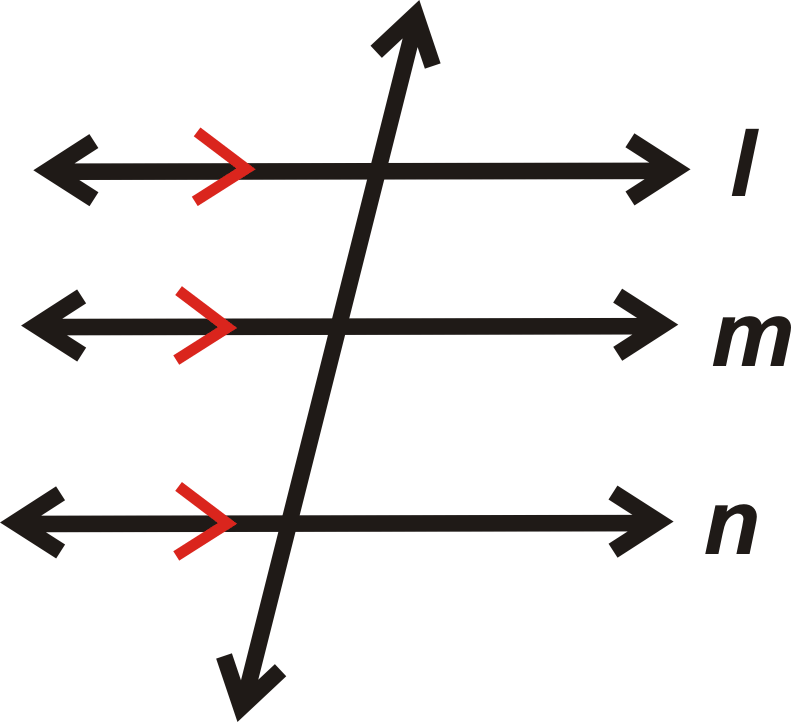
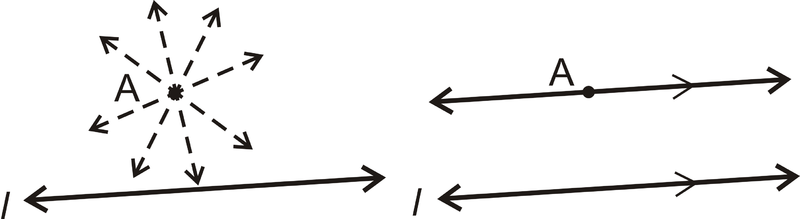
Postulado: Para cualquier línea y un punto que no esté en la línea, hay una línea paralela a esta línea a través del punto. Hay infinitamente muchas líneas que atraviesan\(A\), pero sólo una que es paralela a la\(l\).
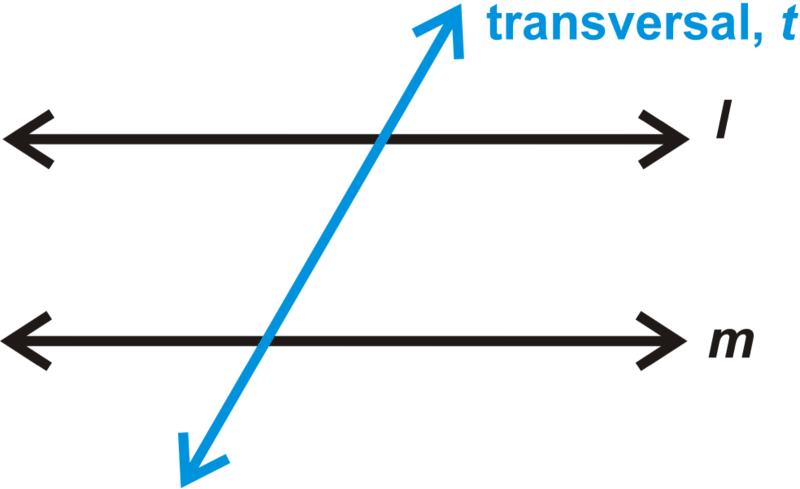
Una transversal es una línea que cruza otras dos líneas. El área entre\(l\) y\(m\) es el interior. El área exterior\(l\) y\(m\) es el exterior.
¿Y si te dieran un par de líneas que nunca se cruzan y se te pidiera describirlas? ¿Qué terminología usarías?
Utilice la figura a continuación para Ejemplos\(\PageIndex{1}\) y\(\PageIndex{2}\). Los dos pentágonos son paralelos y todos los lados rectangulares son perpendiculares a ambos.
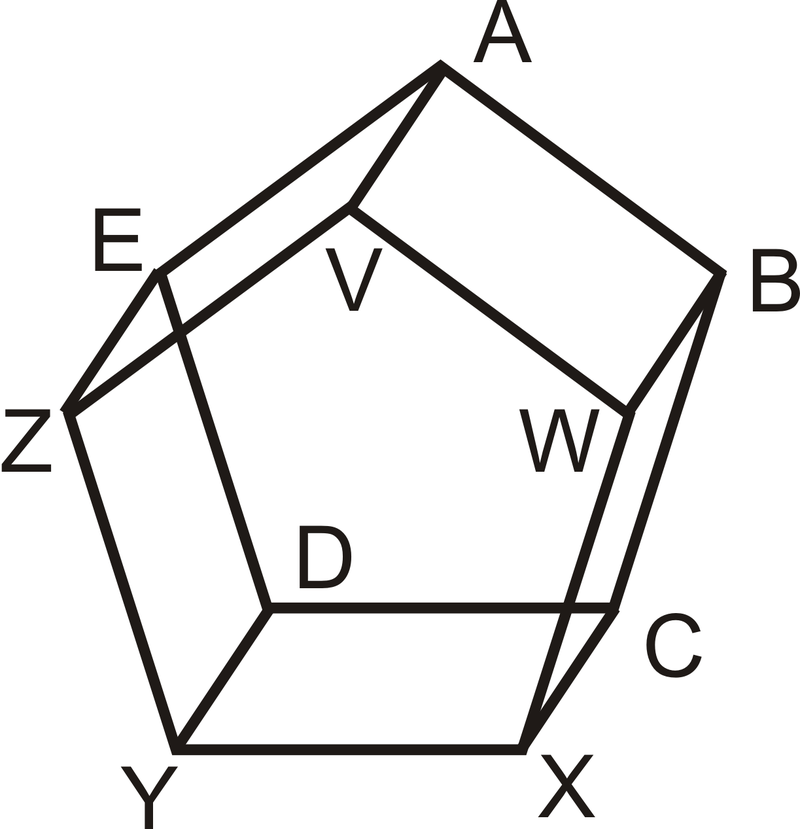
Ejemplo\(\PageIndex{1}\)
Encuentra dos pares de líneas sesgadas.
Solución
\(\overline{ZV}\)y\(\overline{WB}\). \(\overline{YD}\)y\(\overline{VW}\)
Ejemplo\(\PageIndex{2}\)
Porque\(\overline{XY}\), ¿cuántas líneas paralelas pasarían por punto\(D\)? Nombra esta (s) línea (s).
Solución
Una línea,\(\overline{CD}\)
Ejemplo\(\PageIndex{3}\)
Verdadero o falso: algunos pares de líneas sesgadas también son paralelas.
Solución
Esto es falso, por definición las líneas sesgadas están en diferentes planos y las líneas paralelas están en el mismo plano. Dos líneas podrían ser sesgadas o paralelas (o ninguna), pero nunca ambas.
Ejemplo\(\PageIndex{4}\)
Usando el cubo de abajo, enumere un par de líneas paralelas.
Solución
Una respuesta posible son las líneas\(\overline{AB}\) y\(\overline{EF}\).
Ejemplo\(\PageIndex{5}\)
Usando el cubo de abajo, enumere un par de líneas sesgadas.
Solución
Una posible respuesta es\(\overline{BD}\) y\(\overline{CG}\).
Revisar
- ¿Cuál de las siguientes es el mejor ejemplo de líneas paralelas?
- Vías Ferroviarias
- Poste de la lámpara y una acera
- Longitud en un globo
- Stonehenge (la estructura de piedra en Escocia)
- ¿Cuál de los siguientes es el mejor ejemplo de líneas sesgadas?
- Techo de una casa
- Autopista en dirección norte y paso elevado hacia el este
- Longitud en un globo
- El puente Golden Gate
Utilice la imagen de abajo para las preguntas 3-5.
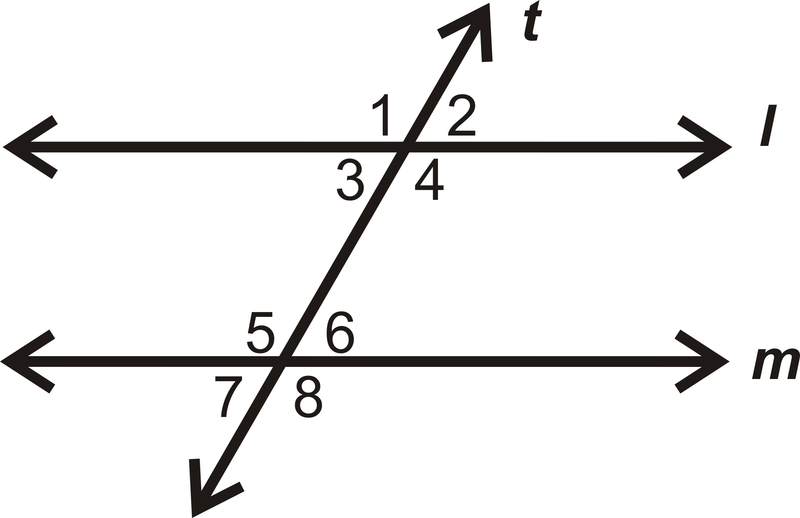
- Si\(m\angle 2=55^{\circ}\), ¿qué otros ángulos conoces?
- Si\(m\angle 5=123^{\circ}\), ¿qué otros ángulos conoces?
- ¿Es\(l\parallel m\)? ¿Por qué o por qué no?
Para 6-10, determinar si la afirmación es verdadera o falsa.
- Si\(p\parallel q \) y\(q\parallel r\), entonces\(p\parallel r\).
- Las líneas sesgadas nunca están en el mismo plano.
- Las líneas sesgadas pueden ser perpendiculares.
- Los planos pueden ser paralelos.
- Las líneas paralelas nunca están en el mismo plano.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.1.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| líneas paralelas | Dos o más líneas que se encuentran en un mismo plano y nunca se cruzan. Las líneas paralelas siempre tendrán la misma pendiente. |
| Líneas sesgadas | Las líneas sesgadas son líneas que están en diferentes planos y nunca se cruzan. |
| transversal | Una transversal es una línea que cruza otras dos líneas. |
| Paralelo | Dos o más líneas son paralelas cuando se encuentran en el mismo plano y nunca se cruzan. Estas líneas siempre tendrán la misma pendiente. |
| sesgar | Para sesgar un conjunto dado significa hacer que la tendencia de los datos favorezca a un extremo u otro |
Recursos adicionales
Elemento Interactivo
Video: Demostrando Líneas Paralelas
Práctica: Preguntas de discusión de líneas paralelas y sesgadas
Ayudas de estudio: Guía de estudio de líneas y ángulos
Pratice: Líneas paralelas y sesgadas
Mundo real: Cortocircuitos: Cómo funcionan los circuitos paralelos