3.4: Ángulos correspondientes
- Page ID
- 107386
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar los ángulos correspondientes como ángulos coincidentes.
Los ángulos correspondientes son dos ángulos que están en el “mismo lugar” con respecto a la transversal pero en líneas diferentes. Imagínese deslizar los cuatro ángulos formados con línea de\(l\) abajo a línea\(m\). Los ángulos que coinciden son los correspondientes.
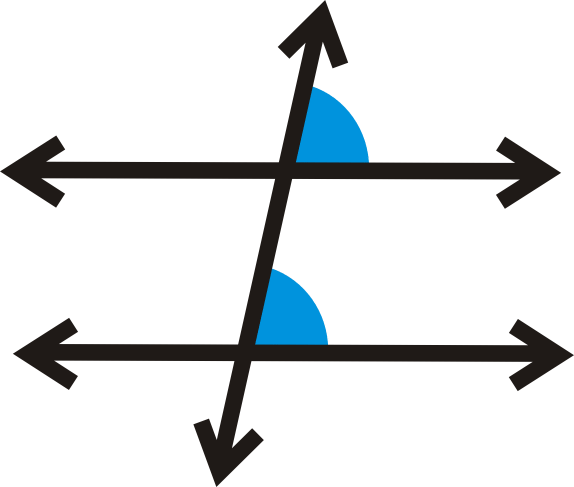
Postulado de ángulos correspondientes: Si dos líneas paralelas son cortadas por una transversal, entonces los ángulos correspondientes son congruentes.
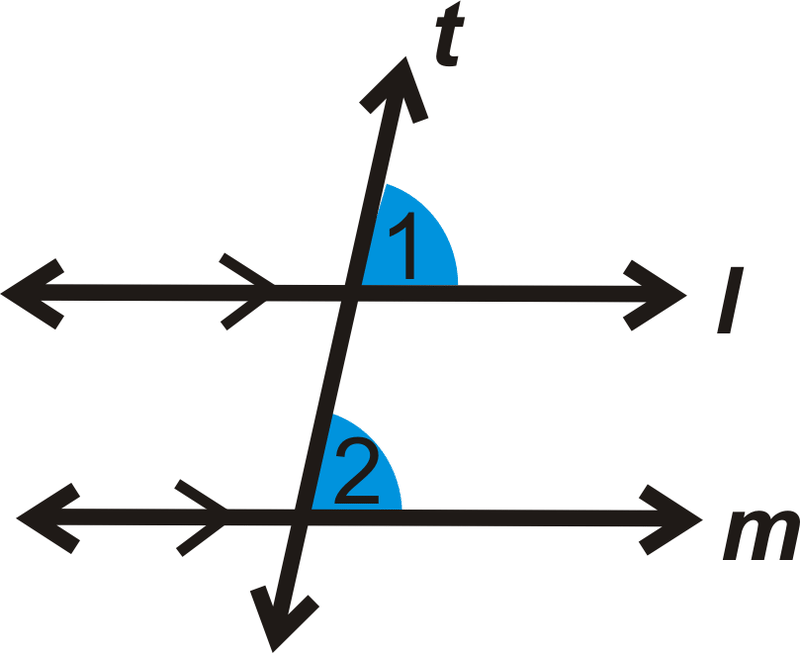
Si\(l \parallel m\), entonces\(\angle 1\cong \angle 2\).
Converse de Ángulos Correspondientes Postulado: Si los ángulos correspondientes son congruentes cuando dos líneas son cortadas por una transversal, entonces las líneas son paralelas.
Si
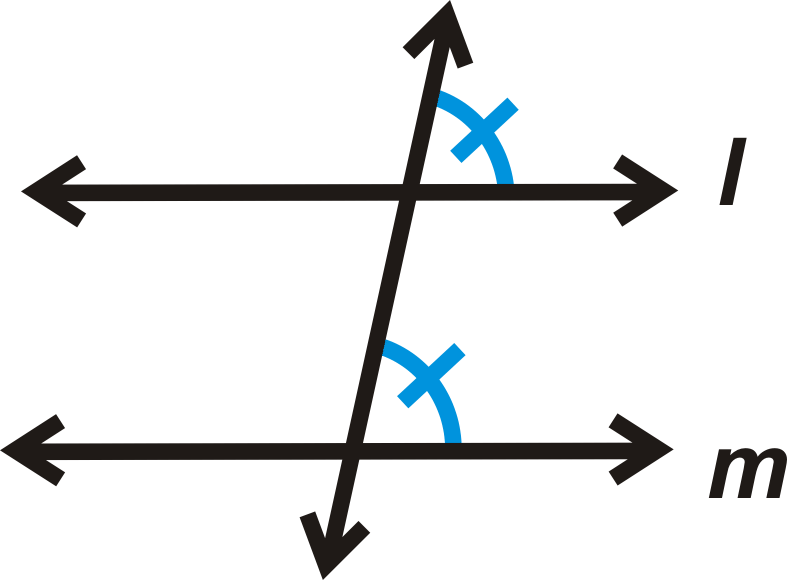
entonces\(l \parallel m\).
¿Y si te presentaran dos ángulos que están en el mismo lugar con respecto a lo transversal pero en líneas diferentes? ¿Cómo describirías estos ángulos y qué podrías concluir sobre sus medidas?
Ejemplo\(\PageIndex{1}\)
Si\(m\angle 2=76^{\circ}\), ¿qué es\(m\angle 6\)?
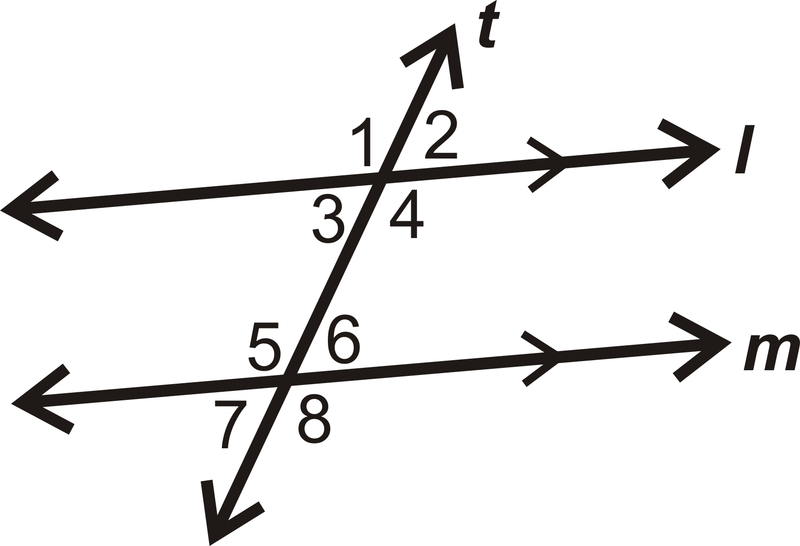
Solución
\(\angle 2\)y\(\angle 6\) son ángulos correspondientes y l||m de las flechas en la figura. \(\angle 2\cong \angle 6\)por el Postulado de Ángulos Correspondientes, lo que significa que\(m\angle 6=76^{\circ}\).
Ejemplo\(\PageIndex{2}\)
Usando las medidas de\ ángulo 2 y\ ángulo 6 del Ejemplo 1, encuentra todas las demás medidas de ángulo.
Solución
Si\(m\angle 2=76^{\circ}\), entonces\(m\angle 1=180^{\circ}−76^{\circ}=104^{\circ}\) (par lineal). \ ángulo 3\ cong\ ángulo 2\) (ángulos verticales), así\(m\angle 3=76^{\circ}\). \(m\angle 4=104^{\circ}\)(ángulo vertical con\ ángulo 1\)).
Por el Postulado de Ángulos Correspondientes\(\angle 1\cong \angle 5\), sabemos\(\angle 2\cong \angle 6\),\(\angle 3\cong \angle 7\),\(\angle 4\cong \angle 8\), y, así\(m\angle 5=104^{\circ}\),\(m\angle 6=76^{\circ}\),\(m\angle 7=76^{\circ}\), y\(m\angle 8=104^{\circ}\).
Ejemplo\(\PageIndex{3}\)
Encuentra el valor de y:
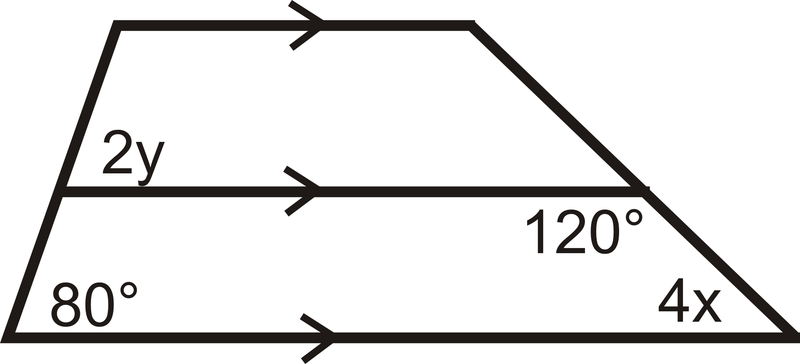
Solución
Las líneas horizontales se marcan paralelas y el ángulo marcado\(2y\) corresponde al ángulo marcado 80 por lo que estos dos ángulos son congruentes. Esto significa eso\(2y=80\) y por lo tanto\(y=40\).
Ejemplo\(\PageIndex{4}\)
Si a||b, ¿qué pares de ángulos son congruentes por el Postulado de Ángulos Correspondientes?
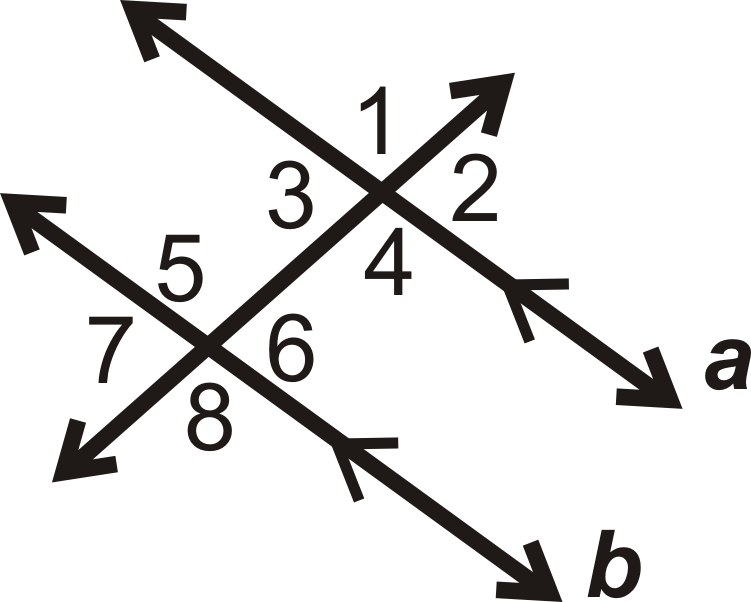
Solución
Hay 4 pares de ángulos correspondientes congruentes:
\(\angle 1\cong \angle 5\),\(\angle 2\cong \angle 6\),\(\angle 3\cong \angle 7\), y\(\angle 4\cong \angle 8\).
Ejemplo\(\PageIndex{5}\)
Si\(m\angle 8=110^{\circ}\) y\(m\angle 4=110^{\circ}\), entonces ¿qué sabemos de líneas\(l\) y\(m\)?
Solución
\(\angle 8\)y\(\angle 4\) son ángulos correspondientes. Ya que\(m\angle 8=m\angle 4\), podemos concluir que l||m.
Revisar
- Determinar si el par angular\(\angle 4\) y\(\angle 2\) es congruente, suplementario o ninguno:
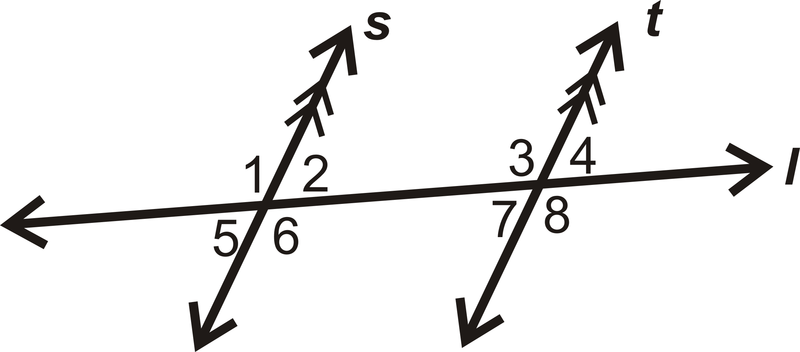
Figura\(\PageIndex{8}\) - Dé dos ejemplos de ángulos correspondientes en el diagrama:
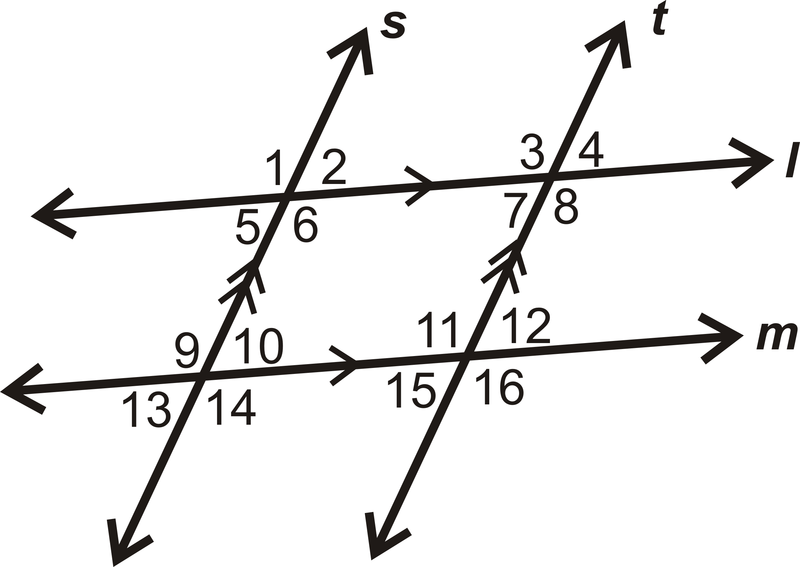
Figura\(\PageIndex{9}\) - Encuentra el valor de\(x\):
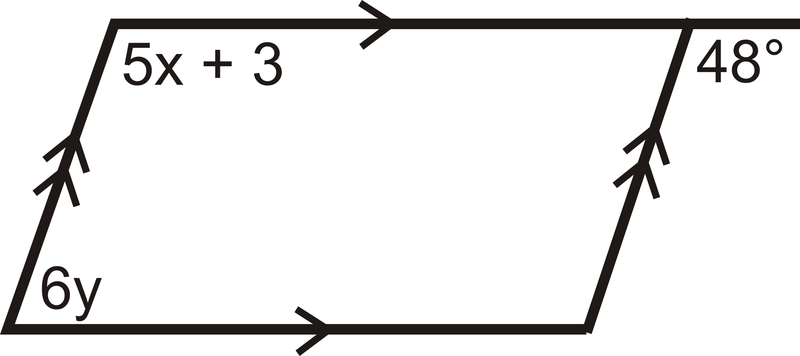
Figura\(\PageIndex{10}\) - ¿Las líneas son paralelas? ¿Por qué o por qué no?
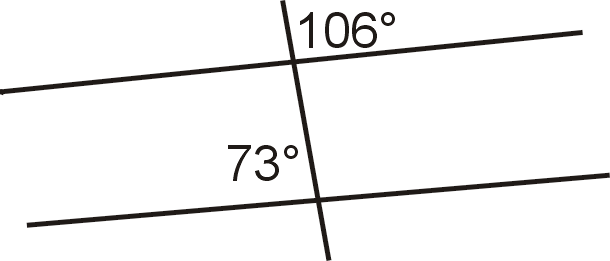
Figura\(\PageIndex{11}\) - ¿Las líneas son paralelas? Justifica tu respuesta.
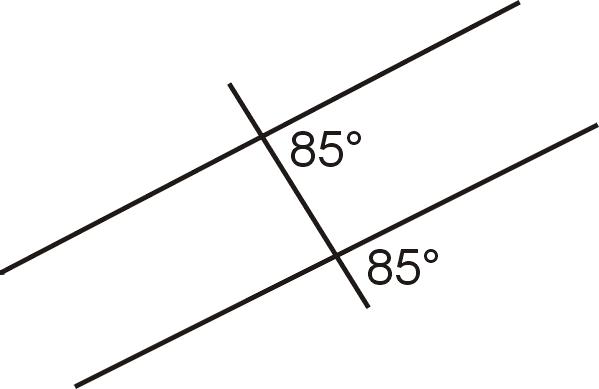
Figura\(\PageIndex{12}\)
Para 6-10, ¿cuál tiene\(x\) que ser el valor de para hacer paralelas las líneas?
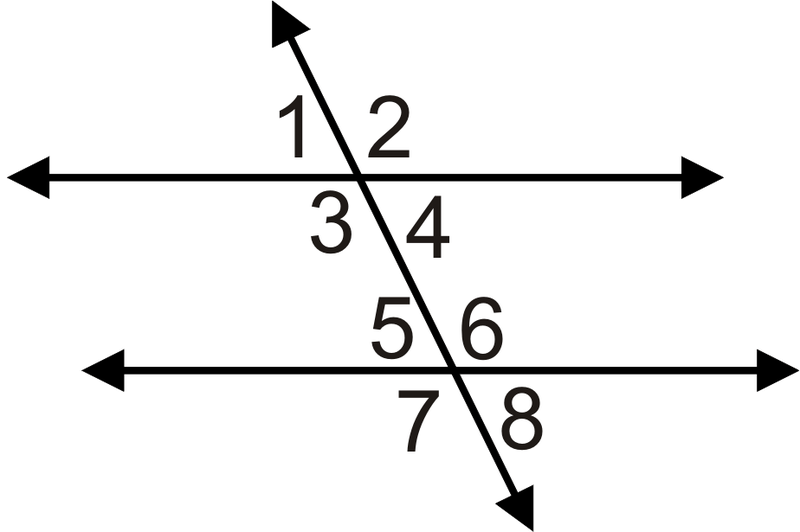
- Si\(m\angle 1=(6x−5)^{\circ}\) y\(m\angle 5=(5x+7)^{\circ}\).
- Si\(m\angle 2=(3x−4)^{\circ}\) y\(m\angle 6=(4x−10)^{\circ}\).
- Si\(m\angle 3=(7x−5)^{\circ}\) y\(m\angle 7=(5x+11)^{\circ}\).
- Si\(m\angle 4=(5x−5)^{\circ}\) y\(m\angle 8=(3x+15)^{\circ}\).
- Si\(m\angle 2=(2x+4)^{\circ}\) y\(m\angle 6=(5x−2)^{\circ}\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.3.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Ángulos correspondientes | Los ángulos correspondientes son dos ángulos que están en la misma posición con respecto a la transversal, pero en líneas diferentes. |
Recurso Adicional
Elemento Interactivo
Video: Principios de Ángulos Correspondientes - Básico
Actividades: Preguntas de discusión de ángulos correspondientes
Ayudas de estudio: Guía de estudio de ángulos y transversales
Práctica: Ángulos correspondientes
Mundo Real: Ángulos Correspondientes