3.5: Ángulos interiores alternos
- Page ID
- 107379
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ángulos en lados opuestos de una transversal, pero dentro de las líneas se cruza.
Los ángulos interiores alternos son dos ángulos que están en el interior de\(l\) y\(m\), pero en lados opuestos de la transversal.
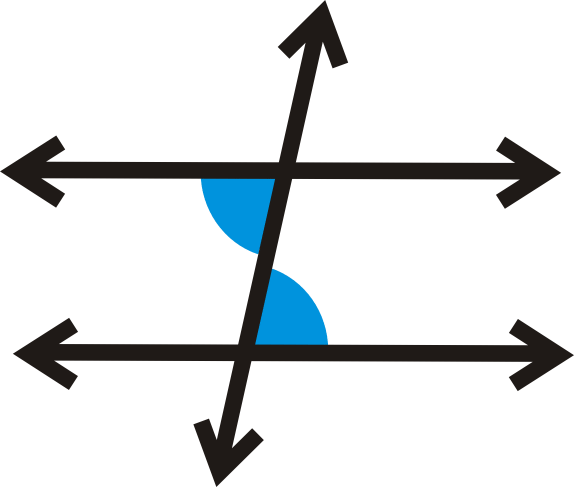
Teorema de ángulos interiores alternos: Si dos líneas paralelas son cortadas por una transversal, entonces los ángulos interiores alternos son congruentes.
Si\(l\parallel m\), entonces\(\angle 1\cong \angle 2\)
Teorema Converse de Ángulos Internos Alternativos: Si dos líneas son cortadas por una transversal y los ángulos interiores alternos son congruentes, entonces las líneas son paralelas.
Si
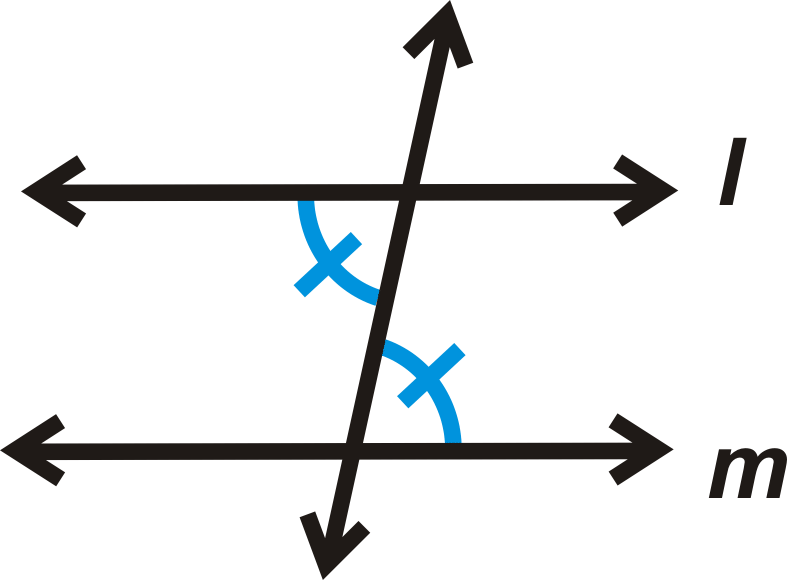
entonces\(l\parallel m\).
¿Y si te presentaran dos ángulos que están en el interior de dos líneas paralelas cortadas por una transversal pero en lados opuestos de la transversal? ¿Cómo describirías estos ángulos y qué podrías concluir sobre sus medidas?
Para Ejemplos\(\PageIndex{1}\) y\(\PageIndex{2}\), utilice la información dada para determinar qué líneas son paralelas. Si no hay ninguno, escriba ninguno. Considera cada pregunta de manera individual.
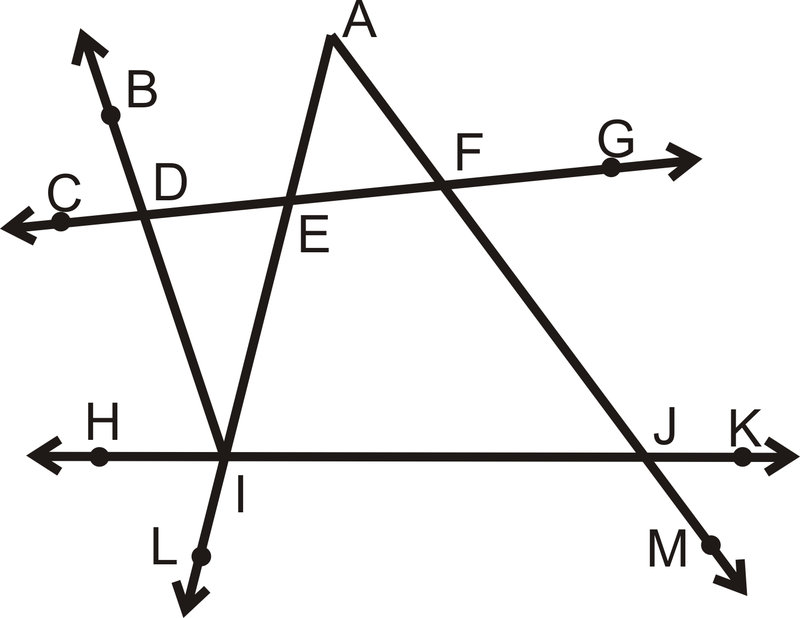
Ejemplo\(\PageIndex{1}\)
\(\angle EAF\cong \angle FJI\)
Solución
Ninguno
Ejemplo\(\PageIndex{2}\)
\(\angle EFJ\cong \angle FJK\)
Solución
\(\overleftarrow{CG} \parallel \overleftarrow{HK}\)
Ejemplo\(\PageIndex{3}\)
Encuentra el valor de\(x\).
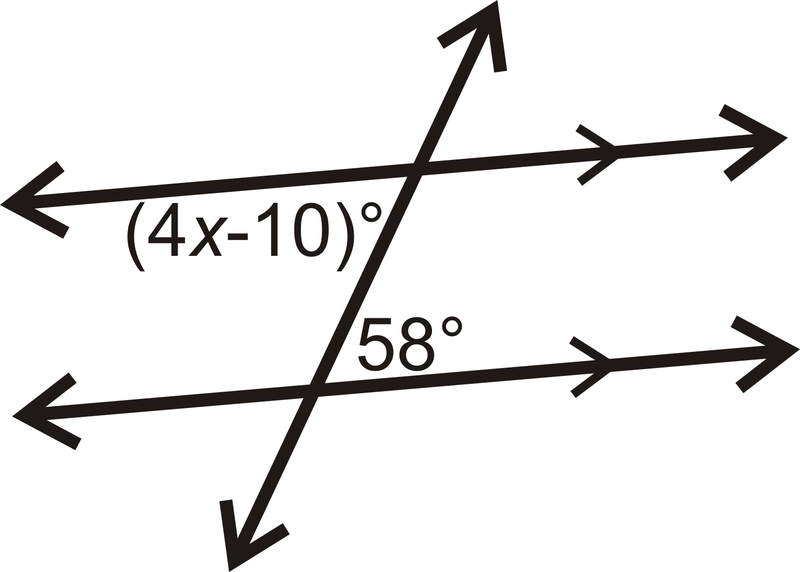
Solución
Los dos ángulos dados son ángulos interiores alternos e iguales.
\(\begin{align*} (4x−10)^{\circ} &=58^{\circ}\\ 4x &=68 \\ x &=17 \end{align*}\)
Ejemplo\(\PageIndex{4}\)
Verdadero o falso: los ángulos interiores alternos son siempre congruentes.
Solución
Esta afirmación es falsa, pero es un error común. Recuerde que los ángulos interiores alternos sólo son congruentes cuando las líneas son paralelas.
Ejemplo\(\PageIndex{5}\)
Los ángulos son ángulos interiores alternos, y deben ser iguales para\(a\parallel b\). Establezca las expresiones iguales entre sí y resuelva.
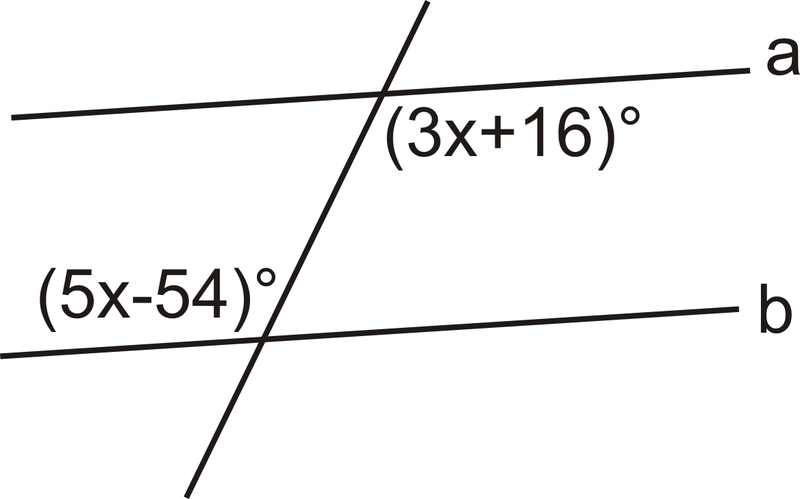
Solución
\(\begin{align*} 3x+16^{\circ} &=5x−54^{\circ} \\ 70&=2x \\ 35 &=x\end{align*}\)
Para hacer\(a\parallel b\),\(x=35\).
Revisar
- ¿Es el par angular\(\angle 6\) y\(\angle 3\) congruente, suplementario o ninguno?
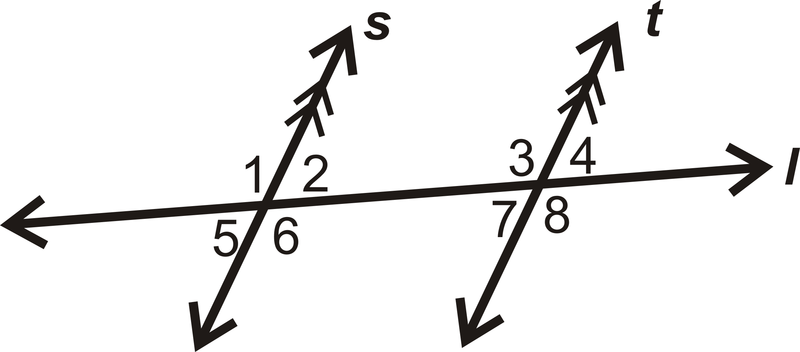
Figura\(\PageIndex{7}\) - Dé dos ejemplos de ángulos interiores alternos en el diagrama:
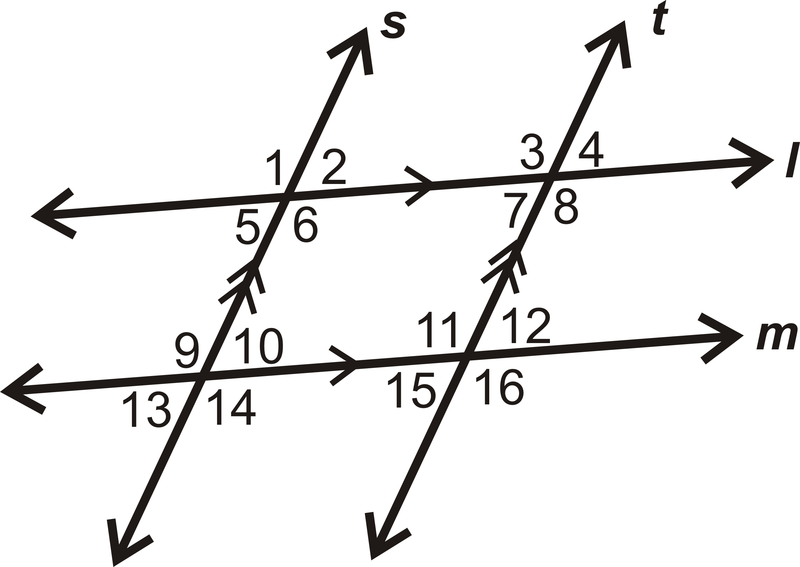
Figura\(\PageIndex{8}\)
Para 3-4, encuentra los valores de\(x\).
-
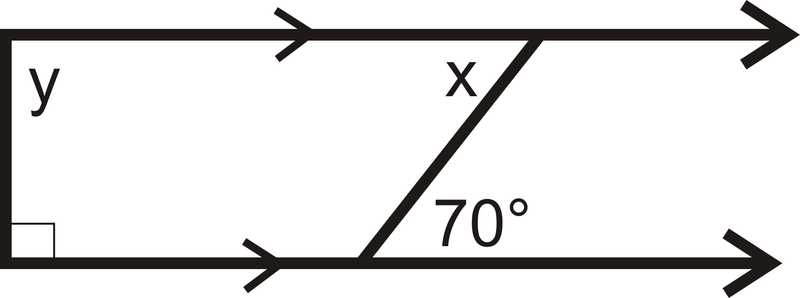Figura\(\PageIndex{9}\) -
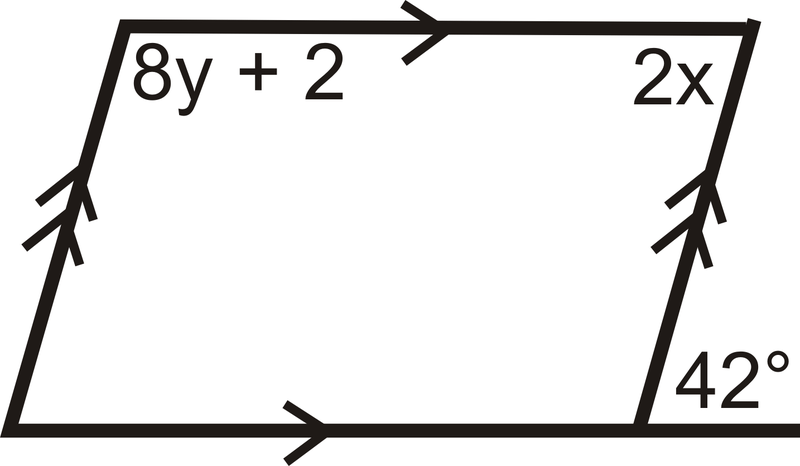Figura\(\PageIndex{10}\)
Para la pregunta 5, usa la imagen de abajo. Encuentra el valor de\(x\).
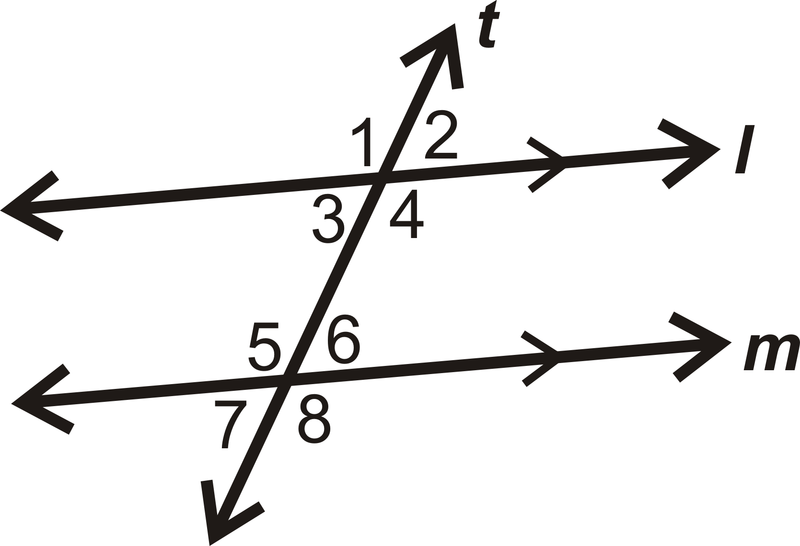
- \(m \angle 4=(5x−33)^{\circ}\),\(m \angle 5=(2x+60)^{\circ}\)
- ¿Son líneas\(l\) y\(m\) paralelas? En caso afirmativo, ¿cómo lo sabes?
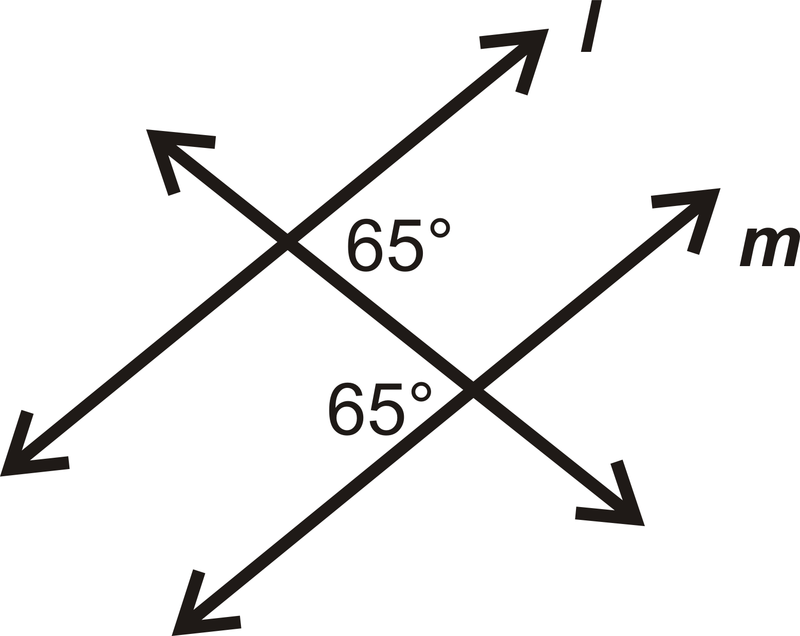Figura\(\PageIndex{12}\)
Para 7-10, ¿cuál tiene que ser el valor de\(x\) para hacer que las líneas sean paralelas?
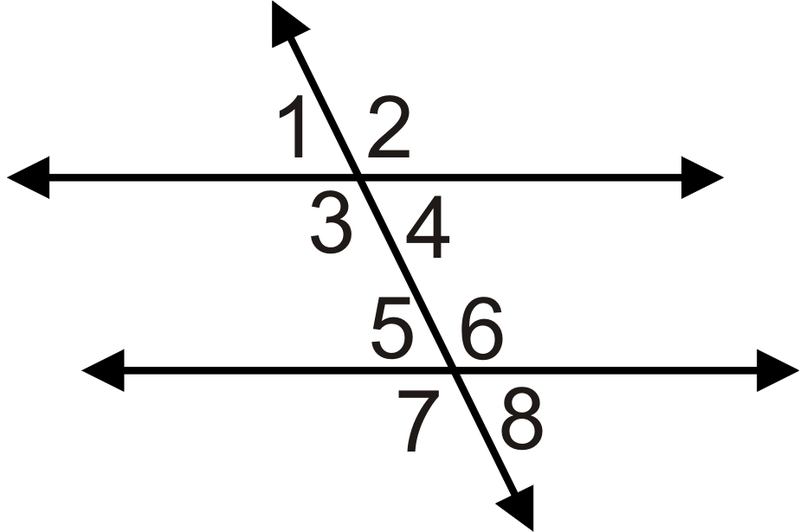
- \(m \angle 4=(3x−7)^{\circ}\)y\(m \angle 5=(5x−21)^{\circ}\)
- \(m \angle 3=(2x−1)^{\circ}\)y\(m \angle 6=(4x−11)^{\circ}\)
- \(m \angle 3=(5x−2)^{\circ}\)y\(m \angle 6=(3x)^{\circ}\)
- \(m \angle 4=(x−7)^{\circ}\)y\(m \angle 5=(5x−31)^{\circ}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.4.
Recursos
vocabulario
| Término | Definición |
|---|---|
| ángulos interiores alternos | Los ángulos interiores alternos son dos ángulos que se encuentran en el interior de dos líneas diferentes, pero en los lados opuestos de la transversal. |
| ángulos exteriores alternos | Los ángulos exteriores alternos son dos ángulos que se encuentran en el exterior de dos líneas diferentes, pero en los lados opuestos de la transversal. |
Recursos adicionales
Video: Principios Alternos de Ángulos Interiores - Básico
Actividades: Preguntas de discusión sobre ángulos interiores alternos
Ayudas de estudio: Guía de estudio de ángulos y transversales
Práctica: Ángulos interiores alternos
Mundo real: ángulos interiores alternos