3.6: Ángulos exteriores alternos
- Page ID
- 107380
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ángulos en lados opuestos de una transversal, pero fuera de las líneas se cruza.
Los ángulos exteriores alternos son dos ángulos que están en el exterior de\(l\) y\(m\), pero en lados opuestos de la transversal.
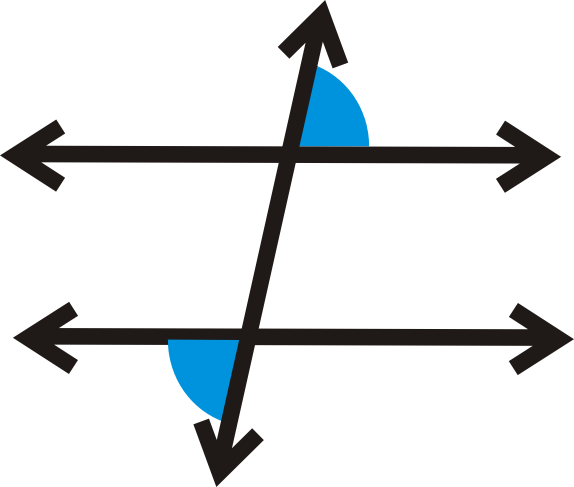
Teorema de ángulos exteriores alternos: Si dos líneas paralelas son cortadas por una transversal, entonces los ángulos exteriores alternos son congruentes.
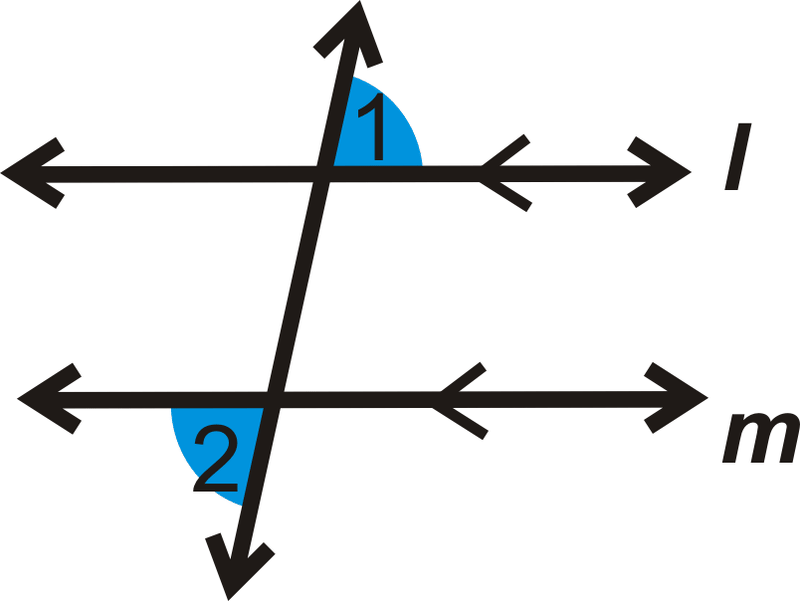
Si\(l \parallel m\), entonces\(\angle 1\cong \angle 2\).
Conversación del Teorema de Ángulos Exteriores Alternados: Si dos líneas son cortadas por una transversal y los ángulos exteriores alternos son congruentes, entonces las líneas son paralelas.
Si
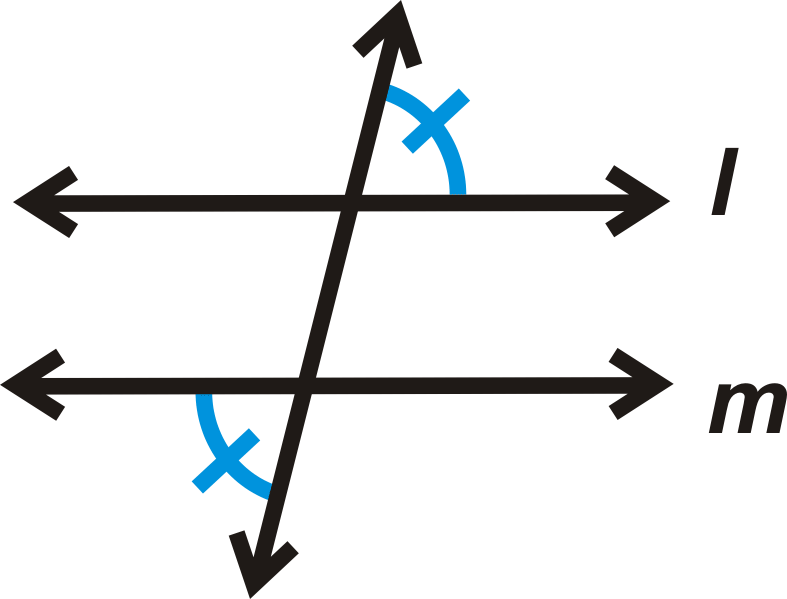
entonces\(l \parallel m\).
¿Y si te presentaran dos ángulos que están en el exterior de dos líneas paralelas cortadas por una transversal pero en lados opuestos de la transversal? ¿Cómo describirías estos ángulos y qué podrías concluir sobre sus medidas?
Para Ejemplos\(\PageIndex{1}\) y\(\PageIndex{2}\), use el siguiente diagrama:
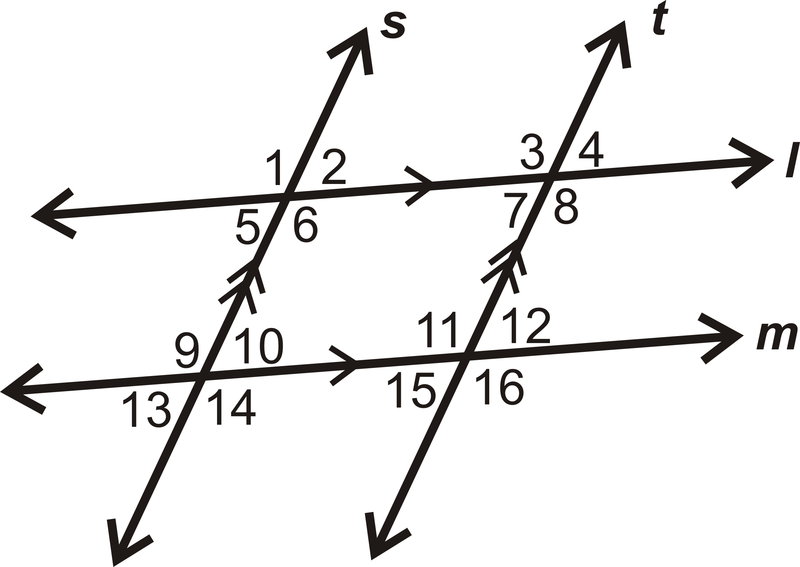
Ejemplo\(\PageIndex{1}\)
Dé un ejemplo de un par de ángulos exteriores alternos.
Solución
\(\angle 1\)y\(\angle 14\) (muchas otras posibilidades)
Ejemplo\(\PageIndex{2}\)
Dé otro ejemplo de un par de ángulos exteriores alternos.
Solución
\(\angle 2\)y\(\angle 13\) (muchas otras posibilidades, deben ser diferentes a la respuesta al Ejemplo 1)
Ejemplo\(\PageIndex{3}\)
Encuentra la medida de cada ángulo y el valor de\) y\).
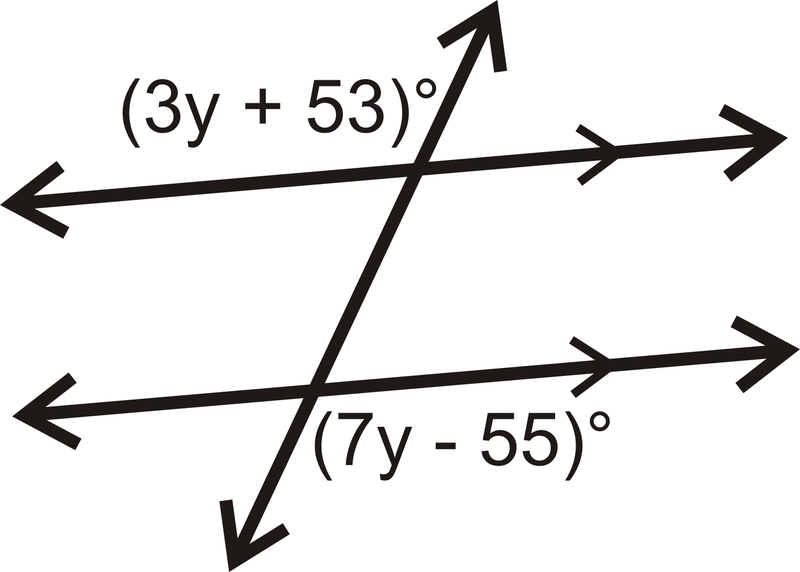
Solución
Los ángulos son ángulos exteriores alternos. Debido a que las líneas son paralelas, los ángulos son iguales.
\(\begin{align*} (3y+53)^{\circ} &=(7y−55)^{\circ} \\ 108 &=4y \\ 27 &=y \end{align*}\)
Si\(y=27, then each angle is \([3(27)+53]^{\circ}=134^{\circ}\).
Ejemplo\(\PageIndex{4}\)
El siguiente mapa muestra tres caminos en la localidad de Julio.
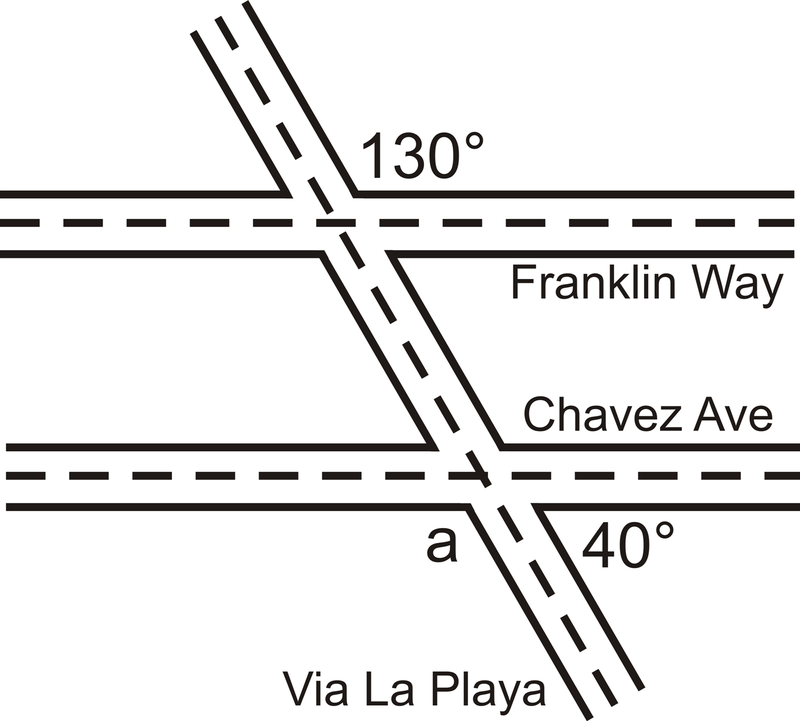
Solución
Julio utilizó una herramienta de topografía para medir dos ángulos en las intersecciones de esta imagen que dibujó (NO a escala). Julio quiere saber si Franklin Way es paralelo a la avenida Chávez.
El\(130^{\circ}\) ángulo y\ ángulo a son ángulos exteriores alternos. Si\(m \angle a=130^{\circ}\), entonces las líneas son paralelas.
\( \begin{align*} \angle a+40^{\circ} &=180^{\circ} & by\:the \:Linear \:Pair \:Postulate \\ \angle a&=140^{\circ} & \end{align*}\)
\(140^{\circ}\neq 130^{\circ}\), por lo que Franklin Way y la avenida Chávez no son calles paralelas.
Ejemplo\(\PageIndex{5}\)
¿Qué líneas son paralelas si\(\angle AFG\cong \angle IJM\)?
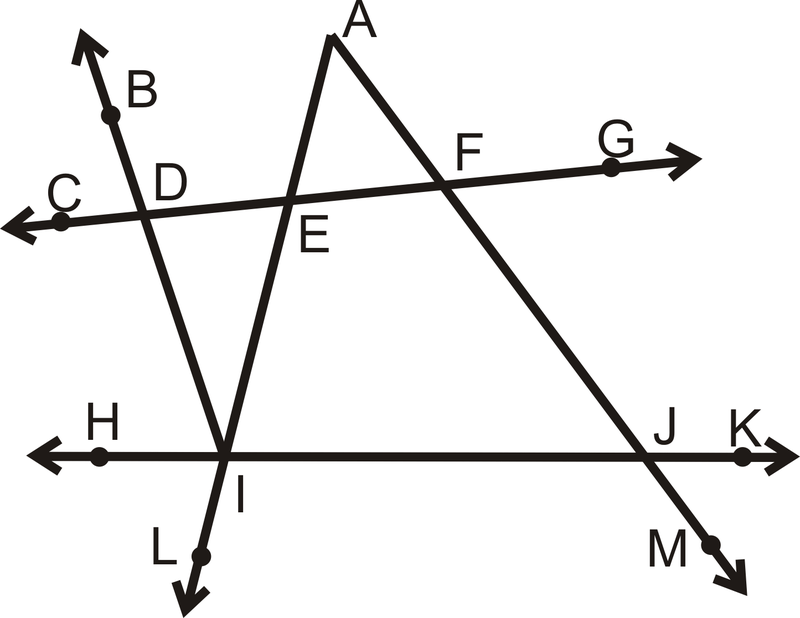
Solución
Estos dos ángulos son ángulos exteriores alternos así que si son congruentes significa que\(\overleftrightarrow{CG}\parallel \overleftrightarrow{HK}\).
Revisar
- Encuentra el valor de\(x\) si\(m \angle 1=(4x+35)^{\circ}\),\(m \angle8=(7x−40)^{\circ}\):
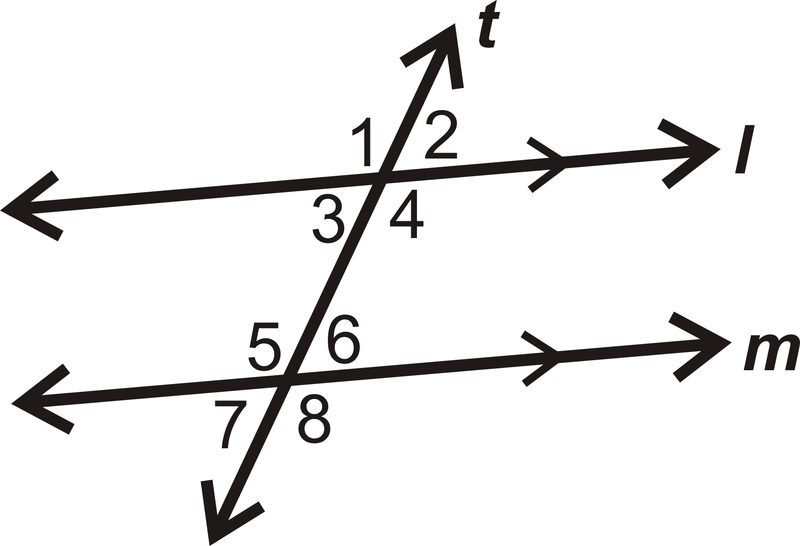
Figura\(\PageIndex{8}\) - ¿Las líneas 1 y 2 son paralelas? ¿Por qué o por qué no?
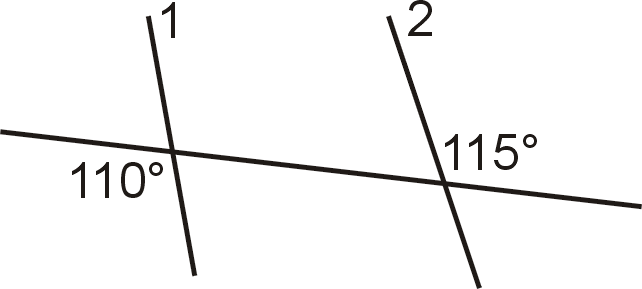
Figura\(\PageIndex{9}\)
Para 3-6, ¿cuál tiene\(x\) que ser el valor de para hacer paralelas las líneas?
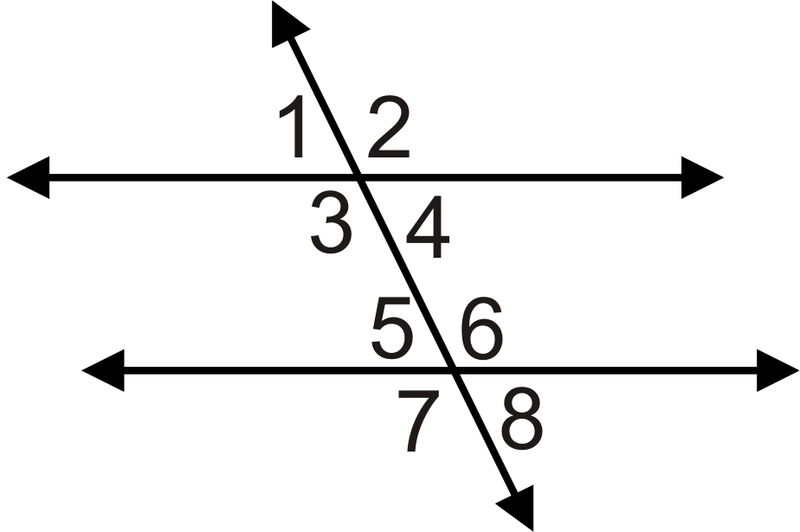
- \(m \angle2=(8x)^{\circ}\)y\(m \angle7=(11x−36)^{\circ}\)
- \(m \angle1=(3x+5)^{\circ}\)y\(m \angle8=(4x−3)^{\circ}\)
- \(m \angle2=(6x−4)^{\circ}\)y\(m \angle7=(5x+10)^{\circ}\)
- \(m \angle1=(2x−5)^{\circ}\)y\(m \angle8=(x)^{\circ}\)
Para 7-10, determinar si la declaración es verdadera o falsa.
- Los ángulos exteriores alternos son siempre congruentes.
- Si los ángulos exteriores alternativos son congruentes, entonces las líneas son paralelas.
- Los ángulos exteriores alternativos están en el interior de dos líneas.
- Los ángulos exteriores alternativos están en lados opuestos de la transversal.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.5.
Recursos
vocabulario
| Término | Definición |
|---|---|
| ángulos exteriores alternos | Los ángulos exteriores alternos son dos ángulos que se encuentran en el exterior de dos líneas diferentes, pero en los lados opuestos de la transversal. |
Recurso Adicional
Elemento Interactivo
Video: Principios Alternativos de Ángulos Exteriores - Básicos
Actividades: Preguntas de discusión sobre ángulos exteriores alternos
Ayudas de estudio: Guía de estudio de ángulos y transversalidades
Práctica: Ángulos exteriores alternos
Mundo real: ángulos exteriores alternos