4.1: Clasificar triángulos
- Page ID
- 107465
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Clasificar los triángulos como agudos, derechos, obtusos o equiangulares y como escalenos, isósceles o equiláteros. Utilice las clasificaciones para encontrar la información faltante.
Clasificación de Triángulos
Un triángulo es cualquier figura cerrada formada por tres segmentos de línea que se cruzan en sus puntos finales. Cada triángulo tiene tres vértices (los puntos donde se encuentran los segmentos), tres lados (los segmentos) y tres ángulos interiores (formados en cada vértice). Todas las siguientes formas son triángulos.
La suma de los ángulos interiores en un triángulo es\(180^{\circ}\). Esto se llama Teorema de la suma del triángulo y se discute más adelante en el concepto de “Teorema de la suma del triángulo”.
Los ángulos pueden clasificarse por su tamaño como agudos, obtusos o rectos. En cualquier triángulo, dos de los ángulos siempre serán agudos. El tercer ángulo puede ser agudo, obtuso o derecho. Clasificamos cada triángulo por este ángulo.
Triángulo recto: Un triángulo con un ángulo recto.
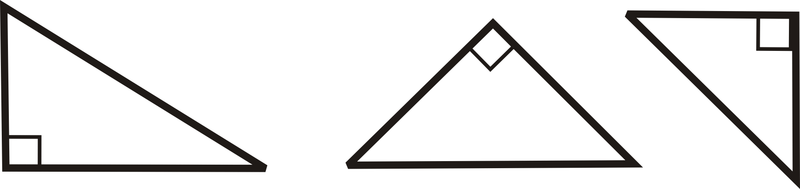
Triángulo Obtuso: Un triángulo con un ángulo obtuso.
Triángulo Agudo: Un triángulo donde los tres ángulos son agudos.
Triángulo Equiangular: Un triángulo donde todos los ángulos son congruentes.
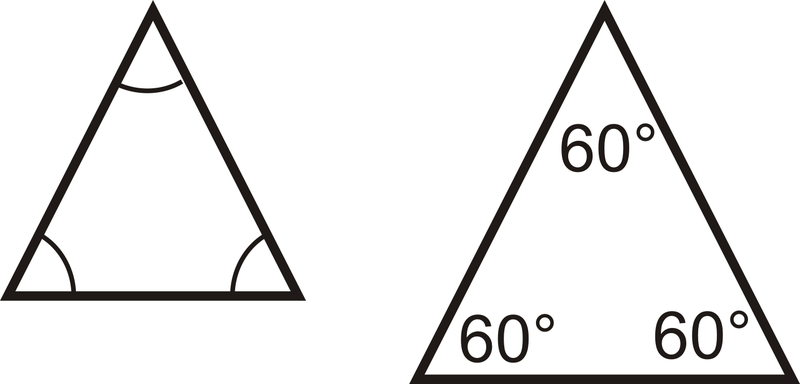
También se puede clasificar un triángulo por sus lados.
Triángulo Escaleno: Un triángulo donde los tres lados son de diferentes longitudes.
Triángulo Isósceles: Un triángulo con al menos dos lados congruentes.
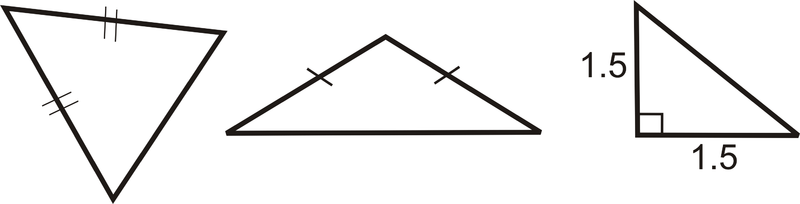
Triángulo Equilátero: Un triángulo con tres lados congruentes.
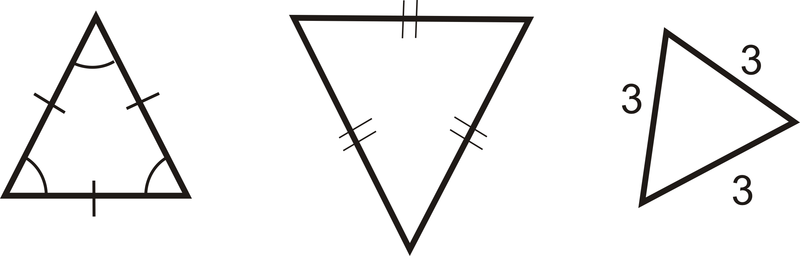
Obsérvese que a partir de las definiciones, un triángulo equilátero es también un triángulo isósceles.
¿Y si te dieran las medidas de ángulo y/o longitudes laterales de un triángulo? ¿Cómo describirías el triángulo a partir de esa información?
Ejemplo\(\PageIndex{1}\)
¿Cuáles de las siguientes figuras no son triángulos?
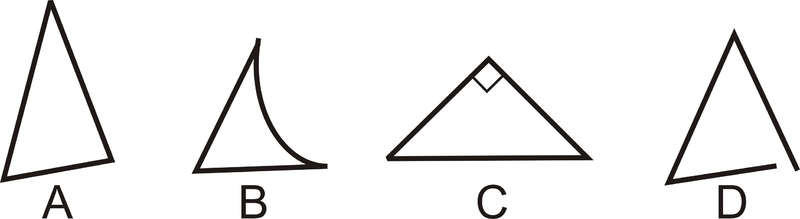Figura\(\PageIndex{9}\)Solución
B no es un triángulo porque tiene un lado curvo. D no está cerrado, por lo que tampoco es un triángulo.
Ejemplo\(\PageIndex{2}\)
¿Cuántos triángulos hay en el siguiente diagrama?
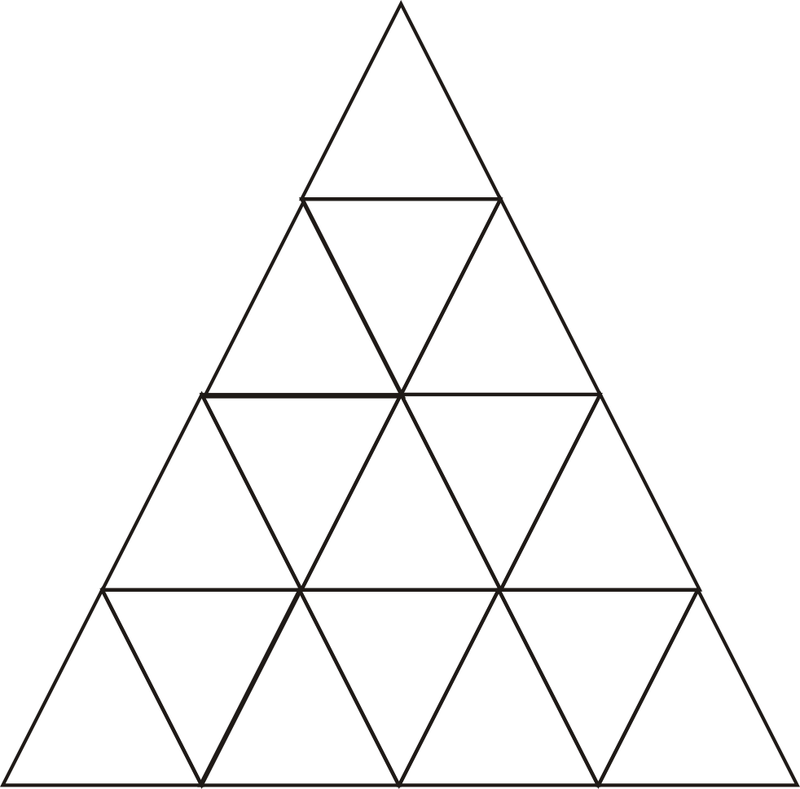Figura\(\PageIndex{10}\)Solución
Comienza contando los triángulos más pequeños, 16.
Ahora cuente los triángulos que están formados por 4 de los triángulos más pequeños, 7.
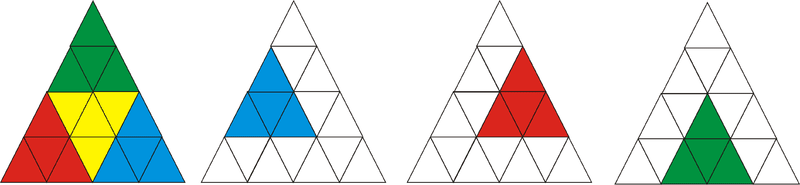Figura\(\PageIndex{11}\)A continuación, cuente los triángulos que están formados por 9 de los triángulos más pequeños, 3.
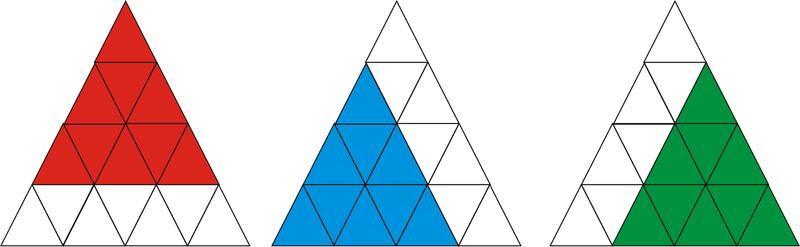
Finalmente, está el triángulo formado por los 16 triángulos más pequeños. Sumando estos números juntos, obtenemos\(16+7+3+1=27\).
Ejemplo\(\PageIndex{3}\)
Verdadero o falso: Un triángulo equilátero es equiangular.
Solución
Cierto. Los triángulos equiláteros tienen ángulos interiores que son todos congruentes por lo que son equiangulares.
Ejemplo\(\PageIndex{4}\)
¿Qué término describe mejor\(\Delta RST\) a continuación?
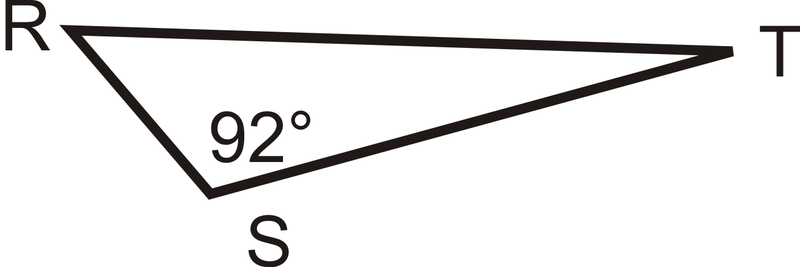
Solución
Este triángulo tiene uno etiquetado ángulo obtuso de\(92^{\circ}\). Los triángulos solo pueden tener un ángulo obtuso, por lo que es un triángulo obtuso.
Ejemplo\(\PageIndex{5}\)
Clasifica el triángulo por sus lados y ángulos.
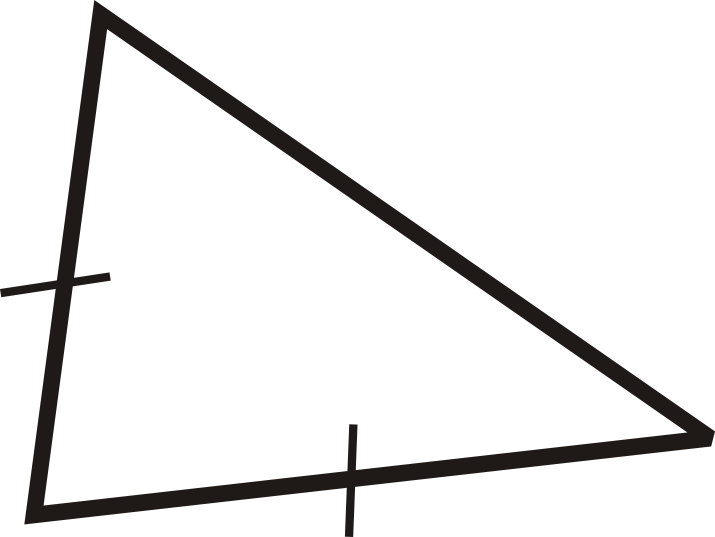
Solución
Vemos que hay dos lados congruentes, por lo que es isósceles. Por los ángulos, todos se ven agudos. Decimos que se trata de un triángulo isósceles agudo.
Revisar
Para las preguntas 1-6, clasifique cada triángulo por sus lados y por sus ángulos.
-
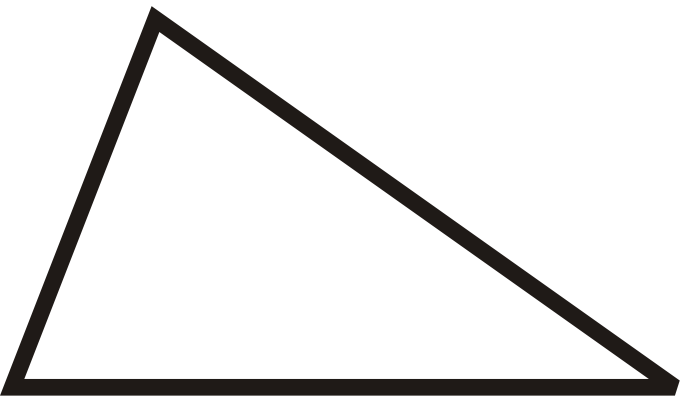
Figura\(\PageIndex{15}\) -
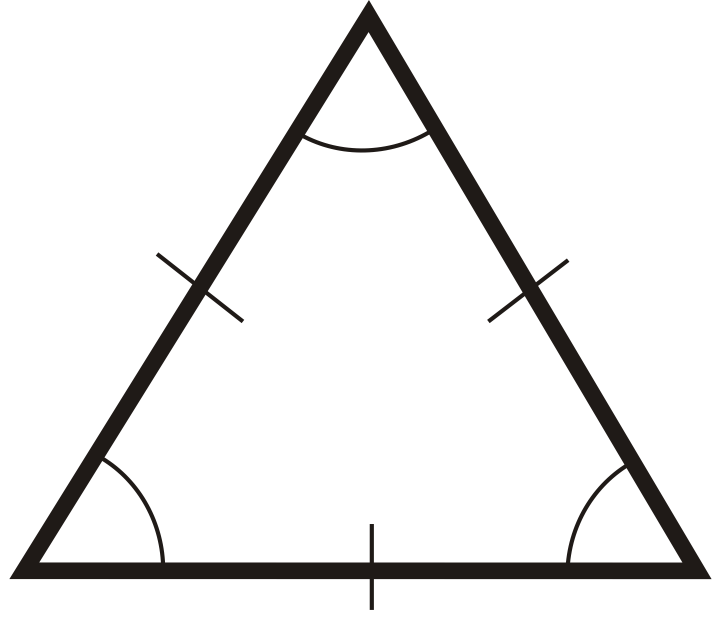
Figura\(\PageIndex{16}\) -
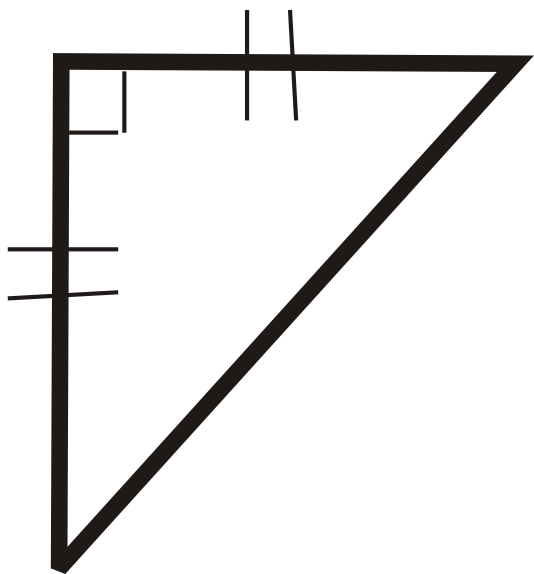
Figura\(\PageIndex{17}\) -
Figura\(\PageIndex{18}\) -
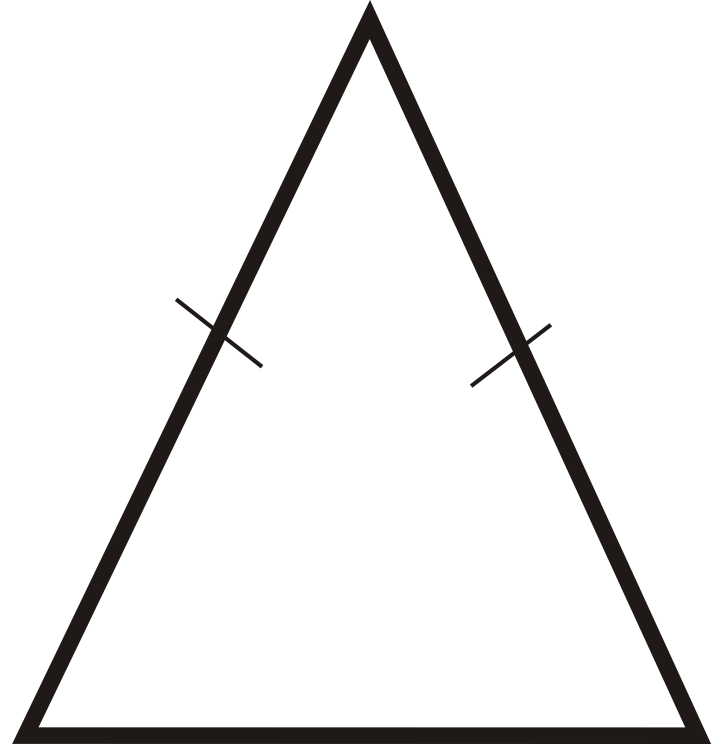
Figura\(\PageIndex{19}\) -
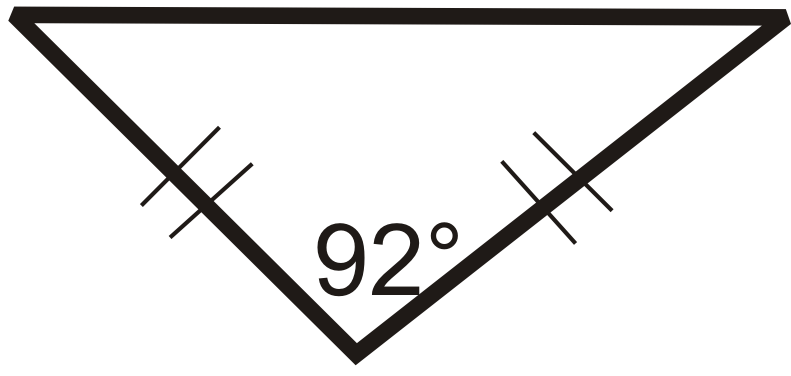
Figura\(\PageIndex{20}\) - ¿Se puede dibujar un triángulo con un ángulo recto y un ángulo obtuso? ¿Por qué o por qué no?
- En un triángulo isósceles, ¿pueden ser obtusos los ángulos opuestos a los lados congruentes?
Para 9-10, determinar si la declaración es verdadera o falsa.
- Los triángulos obtusos pueden ser isósceles.
- Un triángulo rectángulo es agudo.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.11.
Recursos
vocabulario
| Término | Definición |
|---|---|
| Triángulo Agudo | Un triángulo agudo tiene tres ángulos que cada uno mide menos de 90 grados. |
| triángulo equiangular | Un triángulo con todos los ángulos congruentes. |
| triángulo equilátero | Un triángulo con tres lados congruentes. |
| Triángulo Isósceles | Un triángulo isósceles es un triángulo en el que exactamente dos lados tienen la misma longitud. |
| Triángulo Obtuso | Un triángulo obtuso es un triángulo con un ángulo que es mayor a 90 grados. |
| Triángulo Escaleno | Un triángulo escaleno es un triángulo en el que los tres lados tienen diferentes longitudes. |
| Triángulo | Un triángulo es un polígono con tres lados y tres ángulos. |
| Ángulos interiores | Los ángulos interiores son los ángulos dentro de una figura. |
| Ángulo recto | Un ángulo recto es un ángulo igual a 90 grados. |
| Equilátero | Un polígono es equilátero si todos sus lados tienen la misma longitud. |
| Equiangular | Un polígono es equiangular si todos los ángulos son de la misma medida. |
Recursos adicionales
Elemento Interactivo
Video: Relaciones angulares y tipos de triángulos
Actividades: Triángulo Clasificación Discusión Preguntas
Ayudas de estudio: Guía de estudio de polígonos
Práctica: Clasificar triángulos
Mundo real: Puentes sobre aguas turbulentas