4.2: Clasificar triángulos por medición de ángulo
- Page ID
- 107561
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar los triángulos como agudos, derechos, obtusos o equiangulares.
Clasificación de Triángulos por Ángulos

La madre de Michael compró un caddie que cabe en una esquina. Ella usa el caddie para guardar sus escobas y trapeadores en la cochera. El caddie de su madre tenía la apariencia de un triángulo rectángulo cuando se veía desde arriba y encajaba perfectamente en la esquina. A Michael le gustaba el caddie, pero no podía darse el lujo de comprar uno como el suyo, así que decidió hacer el suyo. Compró madera y clavos y la armó, pero cuando trató de ponerla en la esquina de su habitación, no encajaba. Mide los ángulos de su caddie y se da cuenta de que la parte superior es el triángulo de abajo:
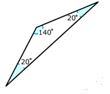
¿Cuál es la clasificación del triángulo de Michael?
En este concepto, aprenderás a usar ángulos para clasificar triángulos.
Clasificación de triángulos por ángulos
El prefijo “tri” significa tres. Triángulo significa tres ángulos.
Para clasificar un triángulo según sus ángulos, debes mirar los ángulos dentro del triángulo. Usa el número de grados en estos ángulos para clasificar el triángulo. Veamos una imagen de un triángulo para explicar.
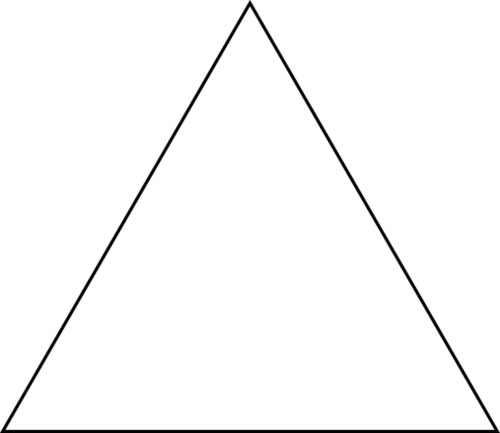
Mira la medida de cada ángulo dentro del triángulo para averiguar qué tipo de triángulo es. Existen cuatro tipos de triángulos basados en medidas de ángulo.
Un triángulo rectángulo es un triángulo que tiene un ángulo recto y dos ángulos agudos. Uno de los ángulos en el triángulo mide\(90^{\circ}\) y los otros dos ángulos son menores a 90. Aquí hay una imagen de un triángulo rectángulo.
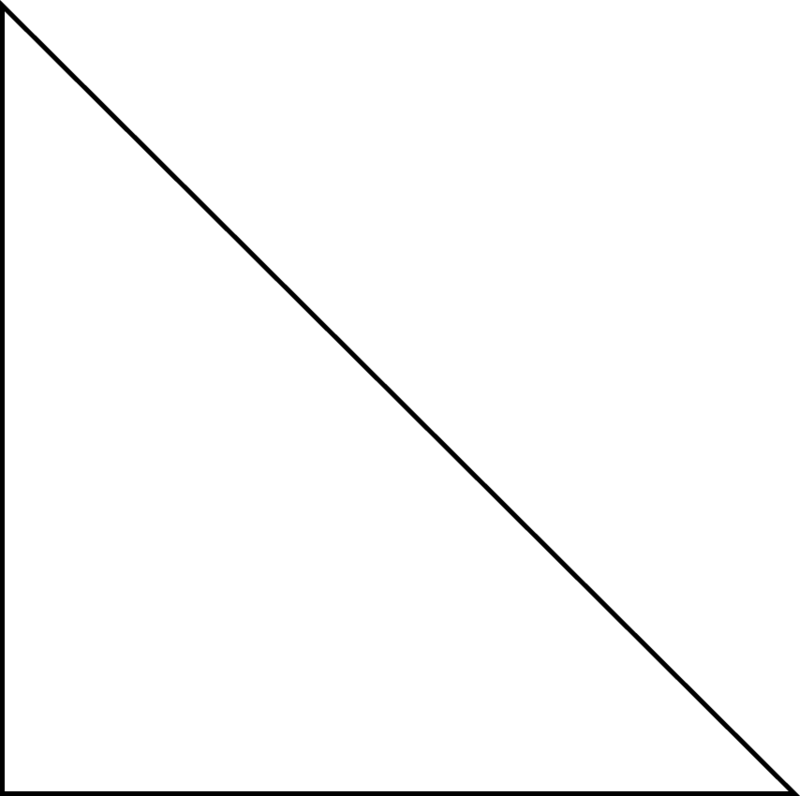
Se puede ver que el ángulo de 90 grados es el que está en la esquina inferior izquierda. Incluso puedes dibujar en la caja pequeña para identificarla como un ángulo de 90 grados. Si miras los otros dos ángulos puedes ver que esos ángulos son menores a 90 grados y son agudos.
Veamos un ejemplo de un ángulo recto.

su triángulo tiene un\(90^{\circ}\) ángulo y dos\(45^{\circ}\) ángulos. Encuentra la suma de los tres ángulos.
\(90+45+45=180^{\circ}\)
La suma de los tres ángulos de un triángulo siempre es igual a\(180^{\circ}\).
En un triángulo equiangular, los tres ángulos son iguales.
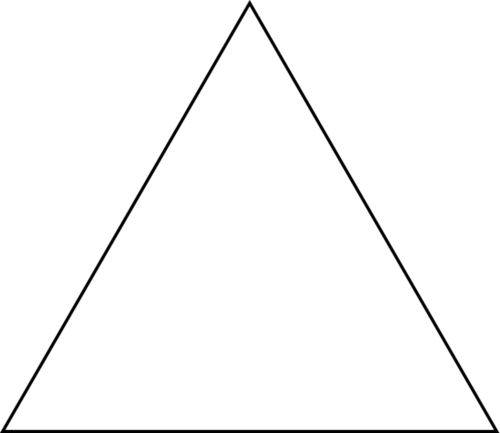
Los tres ángulos de este triángulo son iguales. Se trata de un triángulo equiangular.
Sabes que la suma de los tres ángulos es igual a\(180^{\circ}\), por lo tanto, para que los tres ángulos sean iguales, cada ángulo debe ser igual a\(60^{\circ}\).
\(60+60+60=180^{\circ}\)
La suma de los ángulos es igual a\(180^{\circ}\).
En un triángulo agudo, los tres ángulos del triángulo son menores a 90 grados. Aquí hay un ejemplo de un triángulo agudo.
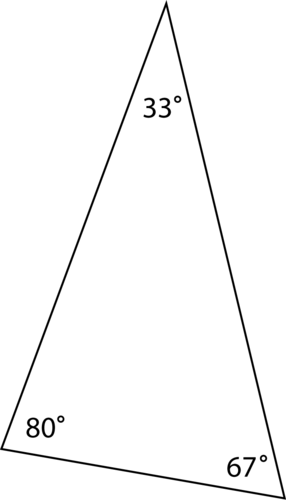
Los tres ángulos miden menos de 90 grados.
\(33+80+67=180^{\circ}\)
La suma de los ángulos es igual a\(180^{\circ}\).
Un triángulo obtuso tiene un ángulo que es mayor que 90 y dos ángulos que son menores a 90.
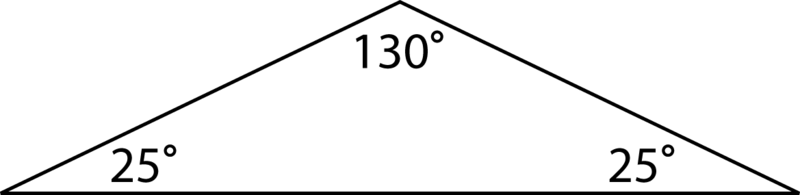
\(130+25+25=180^{\circ}\)
La suma de los ángulos es igual a\(180^{\circ}\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Michael y su caddie.
Intentó construir un caddie como el caddie de su madre. Su caddie parecía un triángulo rectángulo desde arriba pero terminó construyendo uno que tenía las siguientes medidas y apariencia desde arriba:

Solución
¿Cuál es la clasificación del triángulo de Michael?
Primero, enumere las medidas del ángulo.
20, 140
A continuación, determine si alguno de los ángulos es igual a 90 grados o mayor a 90 grados.
Sí, un ángulo es mayor que 90 grados
Después, clasifique el triángulo.
Obtuso
La respuesta es un triángulo obtuso. Michael creó un triángulo obtuso en lugar de un triángulo rectángulo.
Ejemplo\(\PageIndex{2}\)
Identificar el tipo de triángulo según sus ángulos.
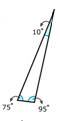
Solución
Primero, enumere las medidas del ángulo.
10, 75, 95
A continuación, determine si alguno de los ángulos es igual a 90 grados o mayor a 90 grados.
Sí, un ángulo es mayor que 90 grados
Después, clasifique el triángulo.
Obtuso
La respuesta es un triángulo obtuso.
Ejemplo\(\PageIndex{3}\)
Identificar el tipo de triángulo según sus ángulos.
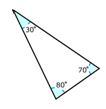
Solución
Primero, enumere las medidas del ángulo.
30, 70 y 80
A continuación, determine si alguno de los ángulos es igual a 90 grados o mayor a 90 grados.
No
Después, clasifique el ángulo.
Aguda
La respuesta es un triángulo agudo.
Ejemplo\(\PageIndex{}\)
Identificar el tipo de triángulo según sus ángulos.
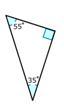
Solución
Primero, enumere las medidas del ángulo.
35, 55 y 90
A continuación, determine si alguno de los ángulos es igual a 90 grados o mayor a 90 grados.
Sí, uno de los ángulos es igual a 90 grados
Después, clasifique el ángulo.
Derecha
La respuesta es un triángulo rectángulo
Ejemplo\(\PageIndex{5}\)
Clasifica el triángulo observando la suma de sus ángulos.
\(40^{\circ}+60^{\circ}+80^{\circ}=180^{\circ}\)
Solución
Primero, enumere las medidas del ángulo.
40, 60 y 80
A continuación, determine si alguno de los ángulos es igual a 90 grados o mayor a 90 grados.
No
Después, clasifique el ángulo.
Aguda
La respuesta es un triángulo agudo.
Revisar
Clasifica cada triángulo según sus ángulos.
-
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{14}\) -
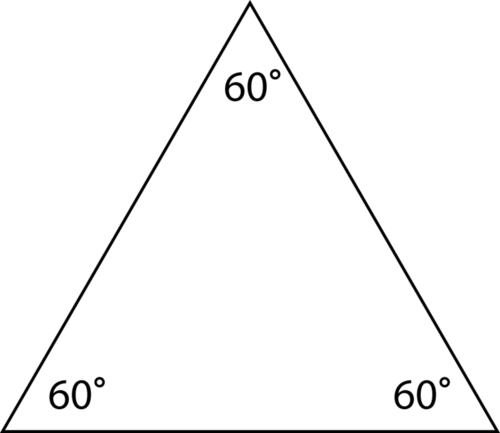
Figura\(\PageIndex{15}\) -
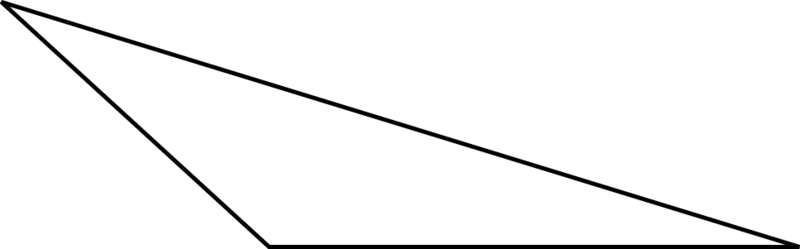
Figura\(\PageIndex{16}\) -
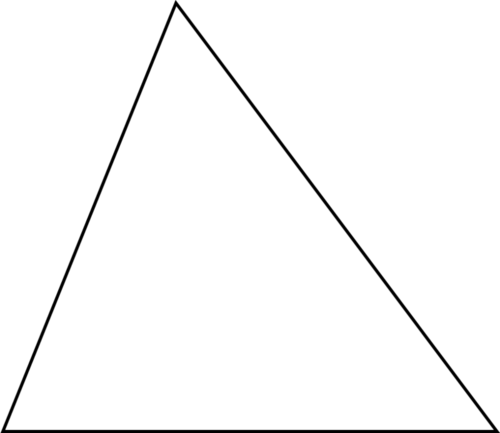
Figura\(\PageIndex{17}\)
Clasifica los siguientes triángulos observando la suma de las medidas del ángulo.
- \(40+55+45=180^{\circ}\)
- \(20+135+25=180^{\circ}\)
- \(30+90+60=180^{\circ}\)
- \(60+60+60=180^{\circ}\)
- \(110+15+55=180^{\circ}\)
- \(105+65+10=180^{\circ}\)
- \(80+55+45=180^{\circ}\)
- \(70+45+65=180^{\circ}\)
- \(145+20+15=180^{\circ}\)
- \(60+80+40=180^{\circ}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.7.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Triángulo Agudo | Un triángulo agudo tiene tres ángulos que cada uno mide menos de 90 grados. |
| Triángulo Equilátero | Un triángulo equilátero es un triángulo en el que los tres lados tienen la misma longitud. |
| Triángulo Obtuso | Un triángulo obtuso es un triángulo con un ángulo que es mayor a 90 grados. |
| Triángulo Recto | Un triángulo rectángulo es un triángulo con un ángulo de 90 grados. |
| Triángulo | Un triángulo es un polígono con tres lados y tres ángulos. |
Recurso Adicional
Elemento Interactivo
Video: Relaciones angulares y tipos de triángulos
Práctica: Clasificar triángulos por medición de ángulo

