4.26: Teorema de la desigualdad del triángulo
- Page ID
- 107457
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)¿Pueden tres longitudes hacer un triángulo? La respuesta es no. Por ejemplo, las longitudes 1, 2, 3 no pueden hacer un triángulo porque\(1+2=3\), así todas estarían en la misma línea. Las longitudes 4, 5, 10 tampoco pueden hacer un triángulo porque\(4+5=9<10\). Mira las fotos a continuación:
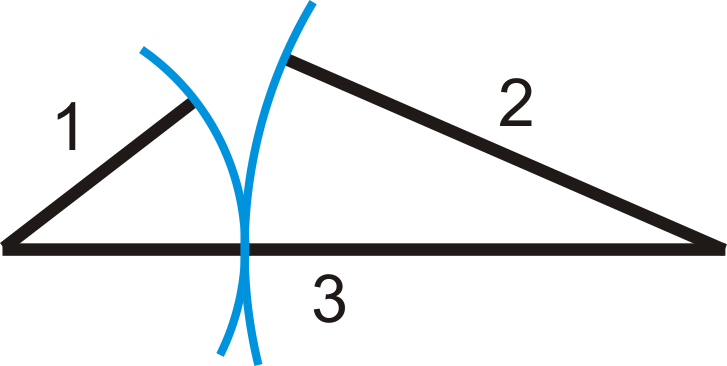
Los arcos muestran que los dos lados nunca se encontrarían para formar un triángulo.
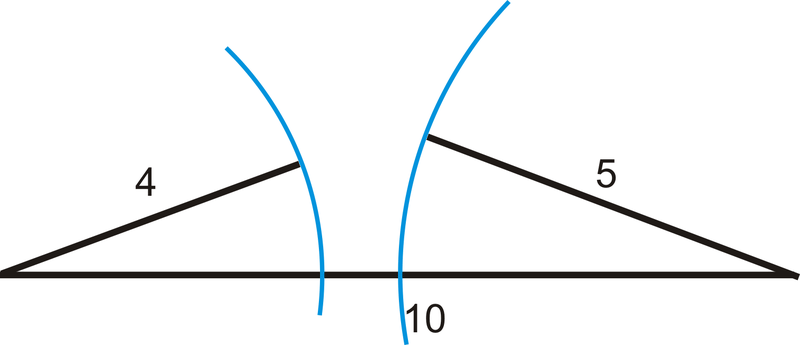
Para hacer un triángulo, dos lados deben sumar para ser mayores que el tercer lado. Esto se llama Teorema de Desigualdad del Triángulo. Esto significa que si conoces dos lados de un triángulo, solo hay ciertas longitudes que podría tener el tercer lado. Si dos lados tienen longitudes\(a\) y\(b\), entonces la longitud del tercer lado, s, tiene el rango\( a−b<s<a+b\).
¿Y si te dieran tres largos, como 5, 7 y 10? ¿Cómo podrías determinar si los lados con estas longitudes forman un triángulo?
Ejemplo\(\PageIndex{1}\)
¿Las longitudes 4.1, 3.5, 7.5 forman un triángulo?
Solución
Usa el Teorema de Desigualdad Triangular Verifique para asegurarse de que los dos números más pequeños sumen para ser mayores que el número más grande.
\(4.1+3.5>7.5\)y\(7.6>7.5\) así y es estas longitudes hacen un triángulo.
Ejemplo\(\PageIndex{2}\)
¿Las longitudes 4, 4, 8 forman un triángulo?
Solución
Usa el Teorema de Desigualdad Triangular Verifique para asegurarse de que los dos números más pequeños sumen para ser mayores que el número más grande.
\(4+8=12\)y\(12>11\) entonces sí estas longitudes hacen un triángulo.
Ejemplo\(\PageIndex{3}\)
¿Las longitudes 4, 11, 8 forman un triángulo?
Solución
Usa el Teorema de Desigualdad Triangular Verifique para asegurarse de que los dos números más pequeños sumen para ser mayores que el número más grande.
\(4+8=12\)y\(12>11\) entonces sí estas longitudes hacen un triángulo.
Ejemplo\(\PageIndex{4}\)
Encuentra la longitud del tercer lado de un triángulo si los otros dos lados son 10 y 6.
Solución
El Teorema de la Desigualdad del Triángulo también puede ayudarte a encontrar el rango del tercer lado. Los dos lados dados son 6 y 10. El tercer lado, s, debe estar entre\(10−6=4\) y\(10+6=16\). En otras palabras, el rango de valores para\(s\) es\(4<s<16\).
Observe que el rango no es menor que 4, y no igual a 4. El tercer lado podría ser 4.1 porque\(4.1+6>10\). Por la misma razón, s no puede ser mayor a 16, pero sí podría\(15.9, 10+6>15.9\).
Ejemplo\(\PageIndex{5}\)
La base de un triángulo isósceles tiene una longitud 24. ¿Qué puedes decir sobre la longitud de cada pierna?
Solución
Para resolver este problema, recuerda que un triángulo isósceles tiene dos lados congruentes (las patas). Tenemos que asegurarnos de que la suma de las longitudes de las piernas sea mayor a 24. En otras palabras, si\(x\) es la longitud de una pierna:
\(\begin{align*} x+x&>24 \\ 2x&>24 \\ x&>12\end{align*}\)
Cada pierna debe tener una longitud mayor a 12.
Revisar
Determina si los conjuntos de longitudes a continuación pueden formar un triángulo. Si no, indiquen por qué.
- 6, 6, 13
- 1, 2, 3
- 7, 8, 10
- 5, 4, 3
- 23, 56, 85
- 30, 40, 50
- 7, 8, 14
- 7, 8, 15
- 7, 8, 14.99
Si se dan dos longitudes de los lados de un triángulo, determine el rango de la longitud del tercer lado.
- 8 y 9
- 4 y 15
- 20 y 32
- 2 y 5
- 10 y 8
- \(x\)y\(2x\)
- Las patas de un triángulo isósceles tienen una longitud de 12 cada una. ¿Qué puedes decir sobre la longitud de la base?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.7.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Teorema de Desigualdad | El Teorema de la Desigualdad del Triángulo establece que para hacer un triángulo, dos lados deben sumar para ser mayores que el tercer lado. |
Recursos adicionales
Elemento Interactivo
Video: Teorema de la Desigualdad
Actividades: Teorema de la Desigualdad del Triángulo
Ayudas de estudio: Guía de estudio de desigualdades en triángulos
Práctica: Teorema de la desigualdad del triángulo
Mundo real: Teorema de la desigualdad del triángulo