4.14: SAS
- Page ID
- 107464
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dos juegos de lados correspondientes y ángulos incluidos prueban triángulos congruentes.
Postulado de ángulo lateral
Si dos lados y el ángulo incluido en un triángulo son congruentes con dos lados y el ángulo incluido en otro triángulo, entonces los dos triángulos son congruentes. (Cuando un ángulo está entre dos lados dados de un polígono, se denomina ángulo incluido).
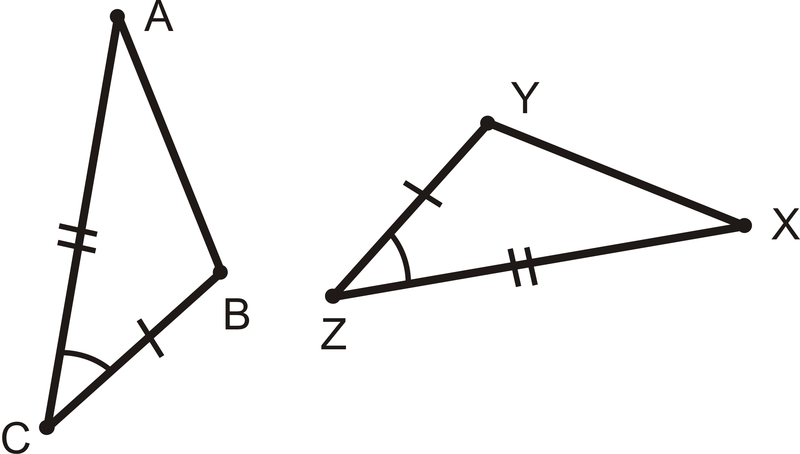
\(\overline{AC}\cong \overline{XZ}\),\(\overline{BC}\cong YZ\), y\(\angle C\cong \angle Z\), entonces\(\Delta ABC\cong \Delta XYZ\).
Esto se llama Postulado Side-Angle-Side (SAS) y es un atajo para demostrar que dos triángulos son congruentes. La colocación de la palabra Ángulo es importante porque indica que el ángulo que se le da es entre los dos lados.
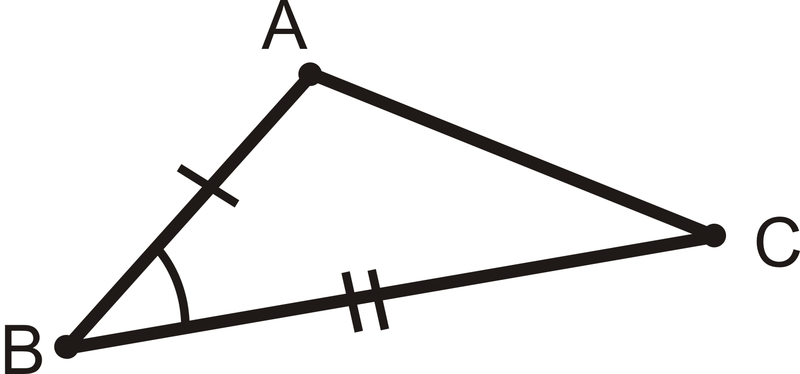
\(\angle B\)sería el ángulo incluido para lados\(\overline{AB}\) y\(\overline{BC}\).
¿Y si te dieran dos triángulos y te proporcionaran solo dos de sus longitudes laterales y la medida del ángulo entre esos dos lados? ¿Cómo podrías determinar si los dos triángulos eran congruentes?
Ejemplo\(\PageIndex{1}\)
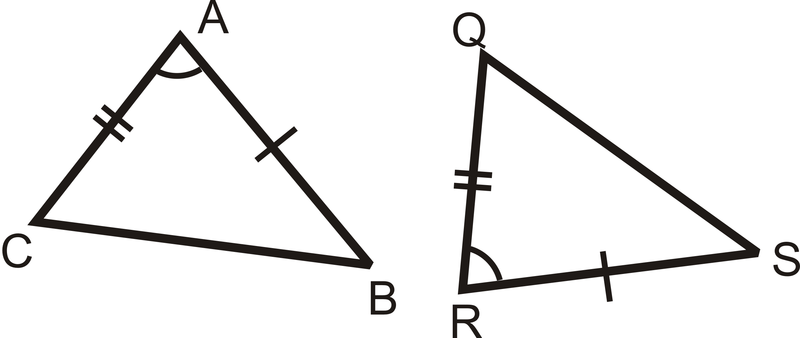
¿El par de triángulos es congruente? Si es así, escribe la declaración de congruencia y por qué.
Solución
El par de triángulos es congruente por el postulado SAS. \(\Delta CAB\cong \Delta QRS\).
Ejemplo\(\PageIndex{2}\)
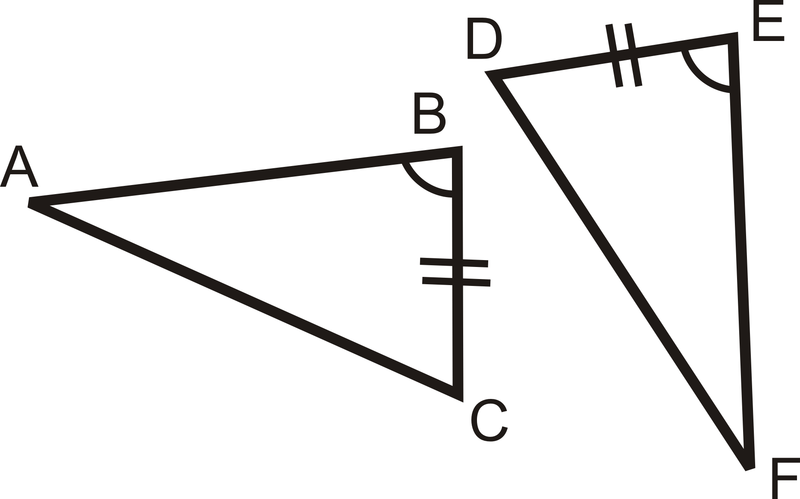
Indique la información adicional necesaria para mostrar que cada par de triángulos es congruente.
Solución
Sabemos que un par de lados y un par de ángulos son congruentes del diagrama. Para saber que los triángulos son congruentes por SAS necesitamos saber que el par de lados del otro lado del ángulo son congruentes. Entonces, necesitamos saber eso\(\overline{EF}\cong \overline{BA}\).
Ejemplo\(\PageIndex{3}\)
Rellene los espacios en blanco en el comprobante a continuación.
Dado:
\(\overline{AB}\cong \overline{DC},\: \overline{BE}\cong \overline{CE}\)
Demostrar:\(\Delta ABE\cong \Delta ACE\)
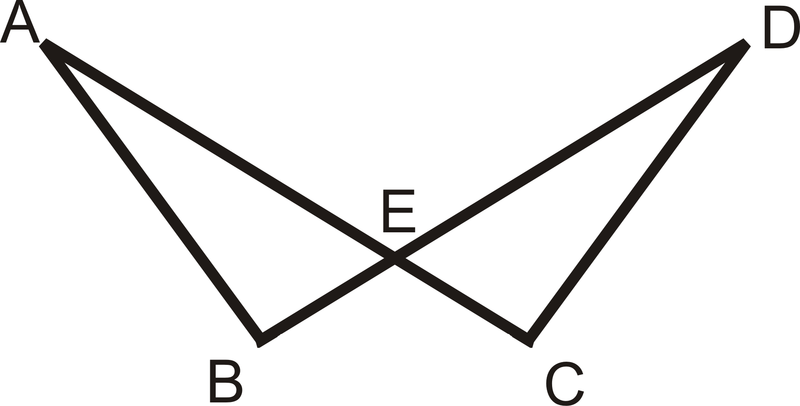
Solución
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(\angle AEB\cong \angle DEC\) | 2. |
| 3. \(\Delta ABE\cong \Delta ACE\) | 3. |
| Declaración | Razón |
|---|---|
| 1. \(\overline{AB}\cong \overline{DC},\: \overline{BE}\cong \overline{CE}\) | 1. Dado |
| 2. \(\angle AEB\cong \angle DEC\) | 2. Teorema de ángulo vertical |
| 3. \(\Delta ABE\cong \Delta ACE\) | 3. Postulado SAS |
Ejemplo\(\PageIndex{4}\)
¿Qué dato adicional necesitas para demostrar que estos dos triángulos son congruentes usando el Postulado SAS,\(\angle ABC\cong \angle LKM\)\(\overline{AB}\cong LK\overline{AB}\),\(\overline{BC}\cong \overline{KM}\), o\(\angle BAC\cong \angle KLM\)?
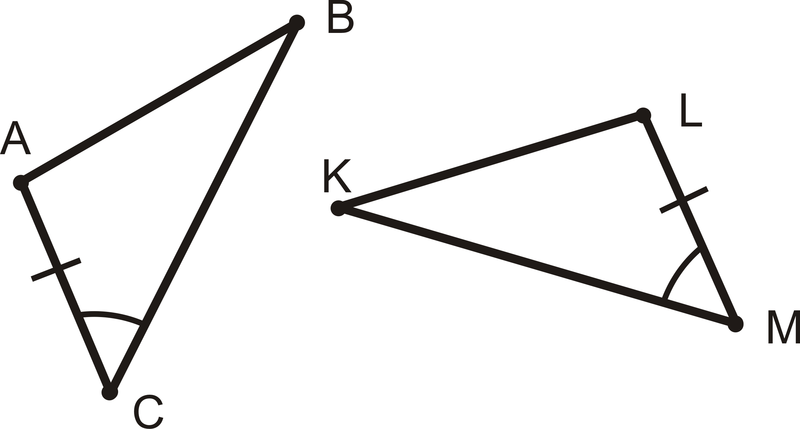
Solución
Para el Postulado SAS, se necesita el lado del otro lado del ángulo. En\(\Delta ABC\), eso es\(\overline{BC}\) y en\(\Delta LKM\) eso es\(\overline{KM}\). La respuesta es\(\overline{BC}\cong \overline{KM}\).
Ejemplo\(\PageIndex{5}\)
¿El par de triángulos es congruente? Si es así, escribe la declaración de congruencia y por qué.
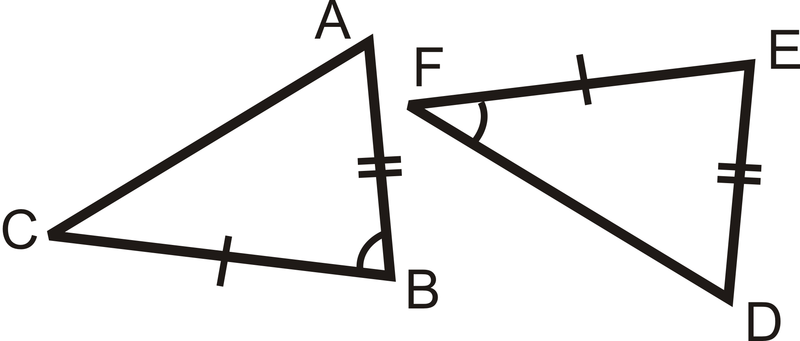
Solución
Si bien los triángulos tienen dos pares de lados y un par de ángulos que son congruentes, el ángulo no está en el mismo lugar en ambos triángulos. El primer triángulo encaja con SAS, pero el segundo triángulo es SSA. No hay suficiente información para que sepamos si estos triángulos son congruentes o no.
Revisar
¿Los pares de triángulos son congruentes? Si es así, escribe la declaración de congruencia y por qué.
-
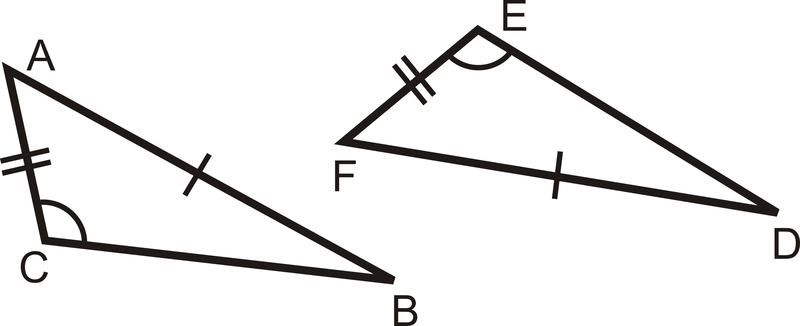
Figura\(\PageIndex{7}\) -
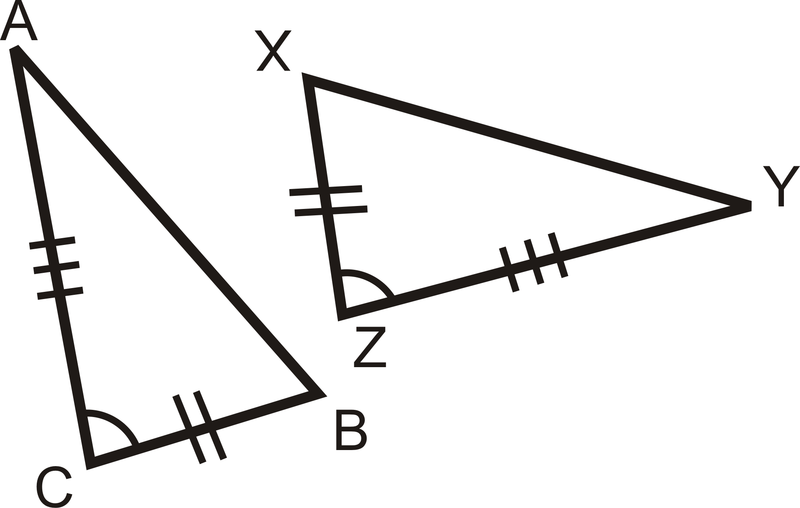
Figura\(\PageIndex{7}\) -
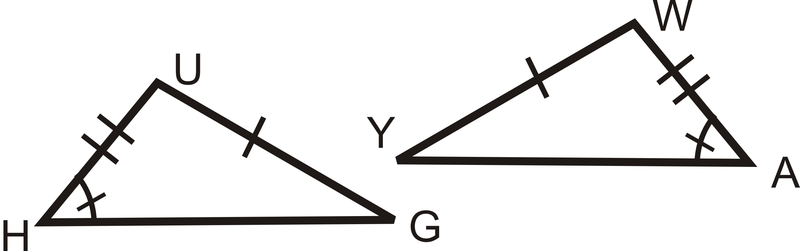
Figura\(\PageIndex{7}\)
Indicar la información adicional necesaria para mostrar que cada par de triángulos es congruente por SAS.
-
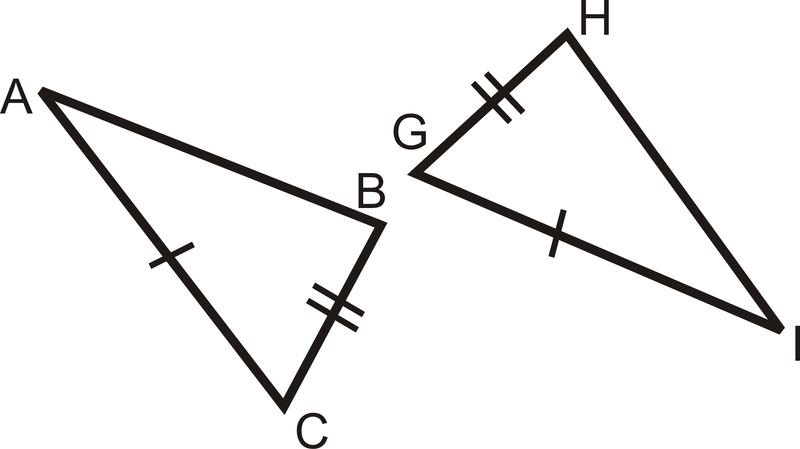
Figura\(\PageIndex{7}\) -
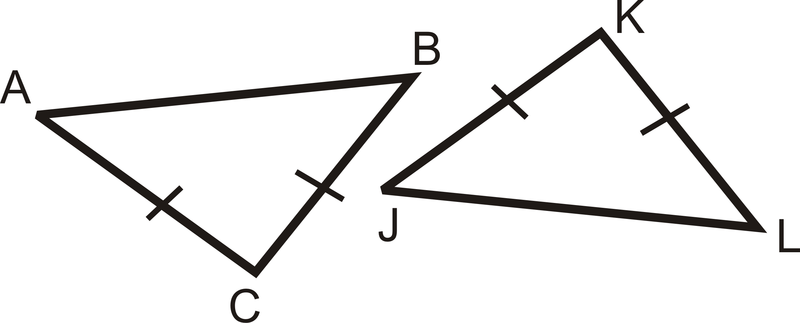
Figura\(\PageIndex{7}\) -
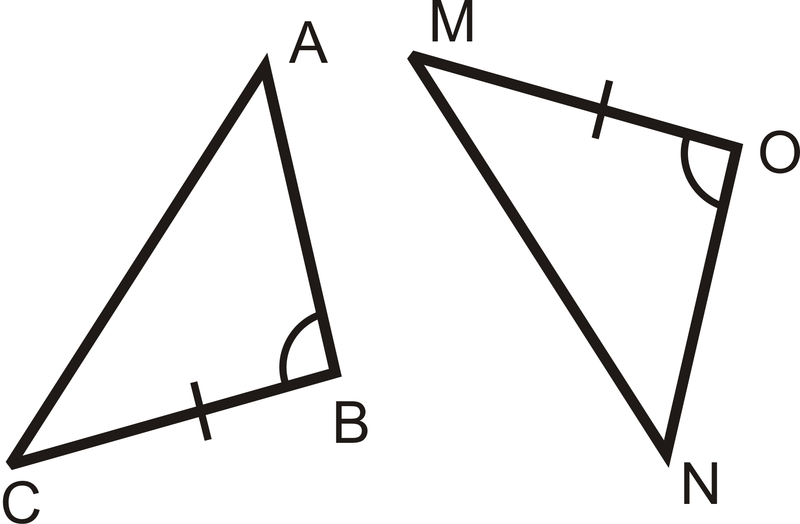
Figura\(\PageIndex{7}\)
Rellene los espacios en blanco en las pruebas a continuación.
- Dado:
- \(B\)es un punto medio de\(\overline{DC}\)
- \(\overline{AB}\perp \overline{DC}\)
Demostrar:\(\Delta ABD\cong \Delta ABC \)
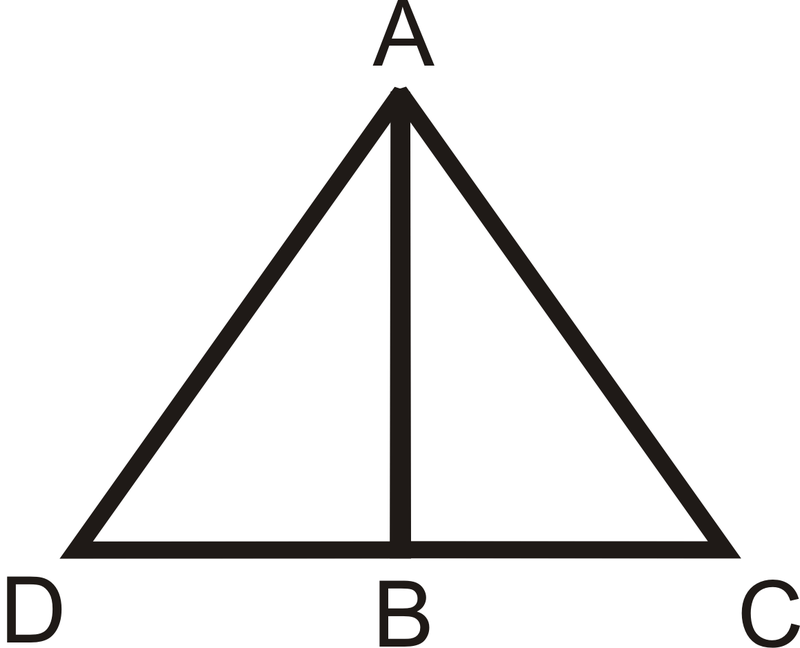
Figura\(\PageIndex{8}\)
| Declaración | Razón |
|---|---|
| 1. \(B\)es un punto medio de\(\overline{DC},\: \overline{AB}\perp \overline{DC}\) | 1. |
| 2. | 2. Definición de un punto medio |
| 3. \(\angle ABD\)y\(\angle ABC\) son ángulos rectos | 3. |
| 4. | 4. Todos los ángulos rectos son\ cong\) |
| 5. | 5. |
| 6. \(\Delta ABD\cong \Delta ABC\) | 6. |
- Dado:
- \(\overline{AB}\)es una bisectriz angular de\(\angle DAC\)
- \(\overline{AD}\cong \overline{AC}\)
Demostrar:\(\Delta ABD\cong \Delta ABC \)

Figura\(\PageIndex{9}\)
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(\angle DAB\cong \angle BAC\) | 2. |
| 3. | 3. reflexivo\(PoC\) |
| 4. \(\Delta ABD\cong \Delta ABC\) | 4. |
- Dado:
- \(B\)es el punto medio de\( \overline{DE}\) y\(\overline{AC}\)
- \(\angle ABE\)es un ángulo recto
Demostrar:\(\Delta ABE\cong \Delta CBD \)
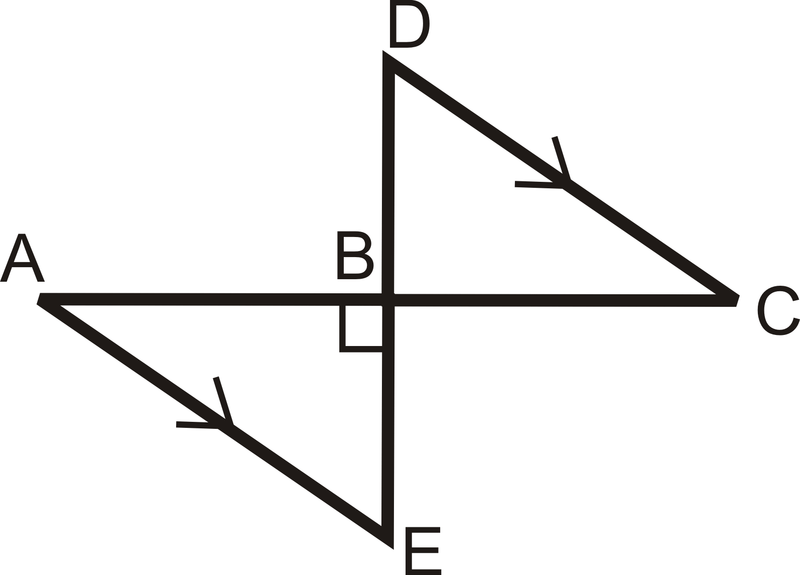
Figura\(\PageIndex{10}\)
| Declaración | Razón |
|---|---|
| 1. | 1. Dado |
| 2. \(\overline{DB}\cong \overline{BE},\: \overline{AB}\cong \overline{BC}\) | 2. |
| 3. | 3. Definición de un ángulo recto |
| 4. | 4. Teorema de ángulo vertical |
| 5. \(\Delta ABE\cong \Delta CBD\) | 5. |
- Dado:
- \(\overline{DB}\)es el ángulo bisectriz de\(\angle ADC\)
- \(\overline{AD}\cong \overline{DC}\)
Demostrar:\(\Delta ABD\cong \Delta CBD\)
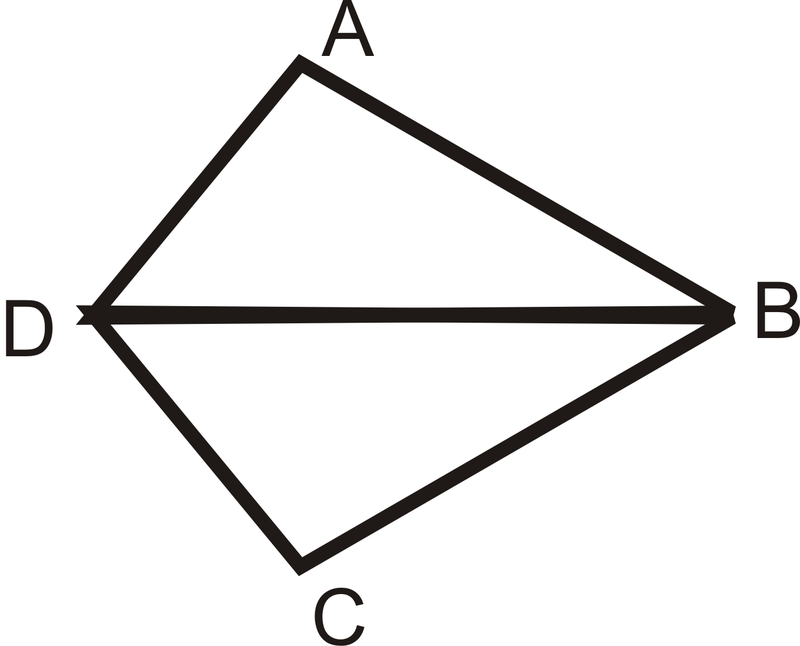
Figura\(\PageIndex{11}\)
| Declaración | Razón |
|---|---|
| 1. | 1. |
| 2. \(\angle ADB \cong \angle BDC\) | 2. |
| 3. | 3. |
| 4. \(\Delta ABD\cong \Delta CBD\) | 4. |
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.7.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulos Base | Los ángulos de base de un triángulo isósceles son los ángulos formados por la base y una pata del triángulo. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Triángulo Equilátero | Un triángulo equilátero es un triángulo en el que los tres lados tienen la misma longitud. |
| Ángulo incluido | El ángulo incluido en un triángulo es el ángulo entre dos lados conocidos. |
| SAS | SAS significa lado, ángulo, lado, y se refiere al hecho de que se conocen dos lados y el ángulo incluido de un triángulo. |
| Ángulo Lateral Triángulo Lateral | Un triángulo lateral de ángulo lateral es un triángulo donde dos de los lados y el ángulo entre ellos son cantidades conocidas. |
| Congruencia del Triángulo | La congruencia del triángulo ocurre si 3 lados en un triángulo son congruentes a 3 lados en otro triángulo. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Recursos adicionales
Elemento interactivo
Video: Introducción a los triángulos congruentes
Actividades: SAS Triangle Congruencia Discusión Preguntas
Ayudas de estudio: Guía de estudio de congruencia triangular
Práctica: SAS
Mundo Real: Congruencia del Triángulo SSS

