4.3: Clasificar triángulos por medición lateral
- Page ID
- 107493
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Clasificar los triángulos como escalenos, isosoles o equalaterales identificando el número de lados iguales.
Clasificación de triángulos por longitudes laterales
Tasha va a navegar con su padre en el viejo barco de su padre. La vela parece un triángulo. Todos los lados de la vela son de diferentes longitudes. Tasha quiere clasificar el triángulo pero no está segura de cómo nombrarlo. Dadas las longitudes laterales del triángulo, ¿cómo puede Tasha clasificar el triángulo?
En este concepto, aprenderás a clasificar los triángulos por sus longitudes laterales.
Clasificación de triángulos por longitudes laterales
Puedes usar las longitudes de los lados para ayudarte a clasificar triángulos.
Veamos cómo clasificar los triángulos según la longitud lateral.
Un triángulo equilátero tiene longitudes laterales iguales. Aquí hay un ejemplo.
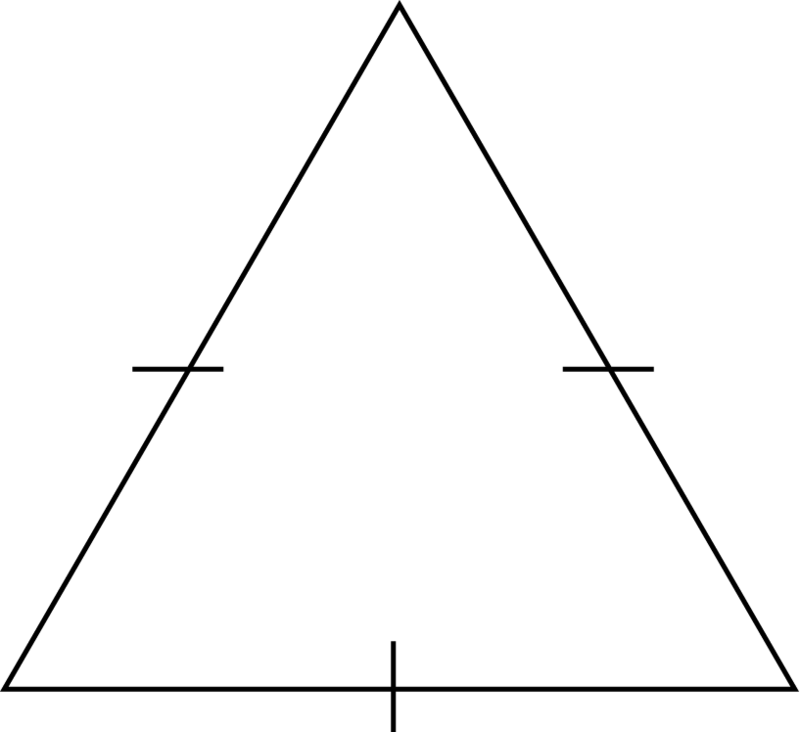
Estas pequeñas líneas te permiten saber que las longitudes laterales son las mismas. A veces las verás y otras no, quizá tengas que descifrarlo por tu cuenta o midiendo con una regla.
Un triángulo escaleno es un triángulo donde las longitudes de los tres lados son diferentes. Aquí hay un ejemplo de un triángulo escaleno.
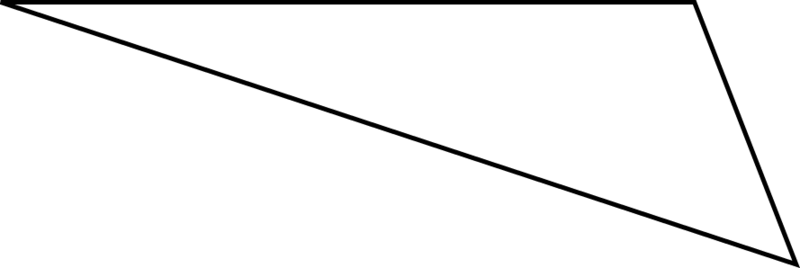
Se puede ver que los tres lados del triángulo son de diferentes longitudes.
Un triángulo isósceles tiene dos longitudes laterales que son iguales y una longitud lateral que es diferente. Aquí hay un ejemplo de un triángulo isósceles.
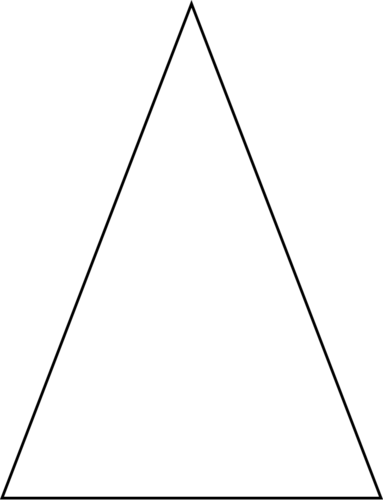Figura\(\PageIndex{4}\)Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Tasha y su vela.
Su vela tiene forma de triángulo con diferentes longitudes laterales. ¿Qué clasificación debe dar Tasha al triángulo?
Solución
Primero, determine si alguna de las longitudes laterales es la misma.
No
Después, clasifique el triángulo.
Escaleno
La respuesta es un triángulo escaleno.
Ejemplo\(\PageIndex{2}\)
Clasificar este triángulo como escaleno, isósceles o equilátero según sus longitudes laterales.
Longitudes laterales, 6 cm, 4 cm, 6 cm
Ángulos 70, 70, 40 grados
Solución
Primero, determine si alguna de las longitudes laterales es la misma.
Sí
A continuación, determine cuántas longitudes de lado son iguales.
Dos
Después, clasifique el triángulo.
Isósceles
La respuesta es un triángulo isósceles.
Ejemplo\(\PageIndex{3}\)
Clasifica este triángulo según sus longitudes laterales.
Solución
Primero, determine si alguna de las longitudes laterales es la misma.
No,
Después, clasifique el triángulo.
Escaleno
La respuesta es un triángulo escaleno.
Ejemplo\(\PageIndex{4}\)
Clasifica el triángulo según sus longitudes laterales.
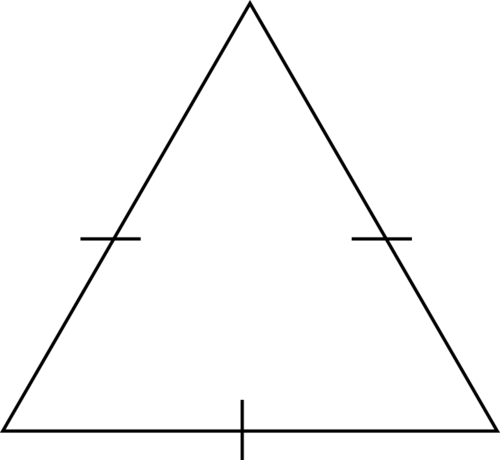Figura\(\PageIndex{5}\)Solución
Primero, determine si alguna de las longitudes laterales es la misma.
Sí
A continuación, determine cuántas longitudes de lado son iguales.
Todas las longitudes laterales son iguales
Después, clasifique el triángulo.
Equilátero
La respuesta es un triángulo equilátero.
Ejemplo\(\PageIndex{5}\)
Clasifica el triángulo según sus longitudes laterales.
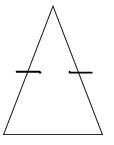
Solución
Primero, determine si alguna de las longitudes laterales es la misma.
Sí
A continuación, determine cuántas longitudes de lado son iguales.
Dos
Después, clasifique el triángulo.
Isósceles
La respuesta es un triángulo isósceles.
Revisar
Responde las siguientes preguntas usando lo que has aprendido sobre los triángulos, sus ángulos y longitudes laterales.
- Si un triángulo es un triángulo rectángulo, entonces ¿cuántos ángulos son agudos?
- ¿Cuántos ángulos en un triángulo rectángulo son ángulos rectos?
- ¿Cuántos grados hay en un triángulo rectángulo?
- ¿Qué es un ángulo obtuso?
- ¿Cuántos ángulos obtusos hay en un triángulo obtuso?
- Si hay un ángulo obtuso, ¿cuántos ángulos son agudos?
- Si un triángulo es equiangular, ¿cuál es la medida de los tres ángulos?
- ¿Qué significa la palabra “ángulo interior”?
- Verdadero o falso. Las longitudes laterales de un triángulo escaleno son todas iguales.
- Verdadero o falso. Las longitudes laterales de un triángulo escaleno son todas diferentes.
- Verdadero o falso. Las longitudes laterales de un triángulo equilátero son todas iguales.
- Verdadero o falso. Un triángulo isósceles tiene dos longitudes laterales iguales y una diferente.
- Verdadero o falso. Un triángulo escaleno también puede ser un triángulo isósceles.
- Verdadero o falso. Un triángulo equilátero también es equiangular.
- Verdadero o falso. Un triángulo escaleno no puede ser un triángulo agudo.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.8.
El vocabulario
| Término | Definición |
|---|---|
| Triángulo Isósceles | Un triángulo isósceles es un triángulo en el que exactamente dos lados tienen la misma longitud. |
| Triángulo Escaleno | Un triángulo escaleno es un triángulo en el que los tres lados tienen diferentes longitudes. |
| Triángulo | Un triángulo es un polígono con tres lados y tres ángulos. |
Recursos adicionales
Elemento Interactivo
Video: Relaciones angulares y tipos de triángulos
Práctica: Clasificar triángulos por medición lateral