4.11: Teorema del Tercer Ángulo
- Page ID
- 107481
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los terceros ángulos son iguales si los otros dos conjuntos son cada uno congruentes.
Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces el tercer par de ángulos también debe ser congruente. Esto se llama Teorema del Tercer Ángulo.
Si\(\angle A\cong \angle D\) y\(\angle B\cong \angle E\), entonces\(\angle C\cong \angle F\).
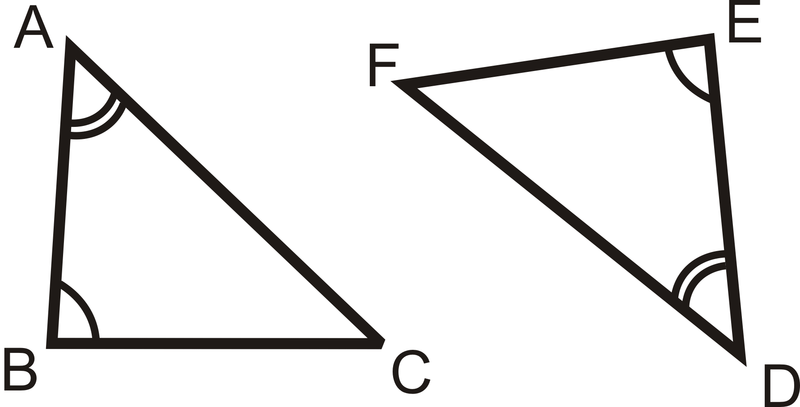
¿Y si te dieron\(\Delta FGH\)\(\Delta XYZ\) y y te dijeron eso\(\angle F\cong \angle X\) y\(\angle G\cong \angle Y\)? ¿Qué conclusión podrías sacar\(\angle H\) y\(\angle Z\)?
Ejemplo\(\PageIndex{1}\)
Determinar la medida de todos los ángulos en cada triángulo.
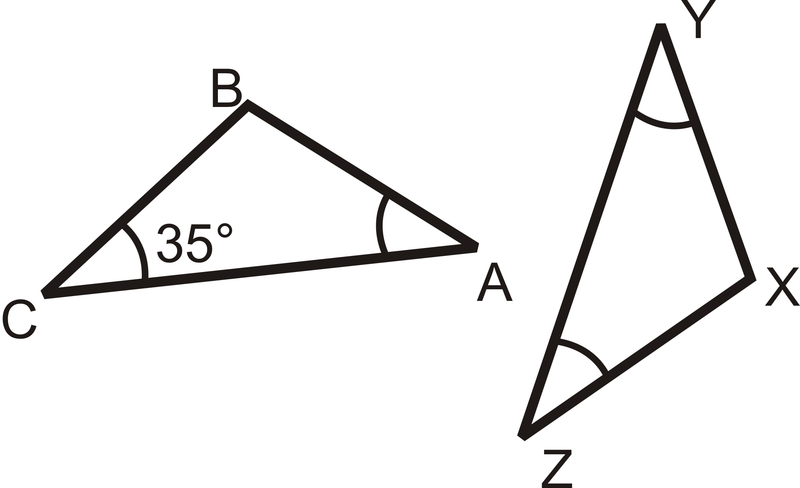
Solución
\(m\angle C=m\angle A=m\angle Y=m\angle Z=35\). Por el teorema de la suma del triángulo\(m\angle B=m\angle X=110\).
Ejemplo\(\PageIndex{2}\)
Determinar la medida de todos los ángulos en cada triángulo.
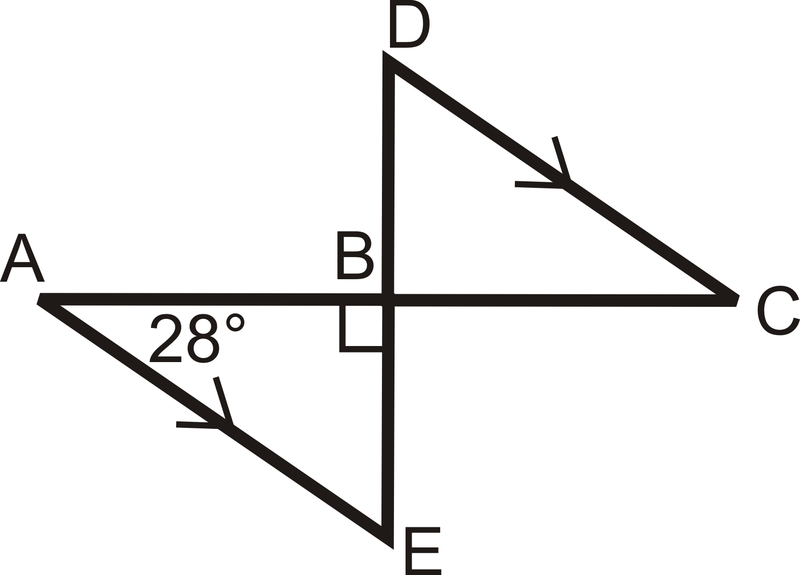
Solución
\(m\angle A=28\),\(m\angle ABE=90\) y por el teorema de la suma del triángulo,\(m\angle E=62\). \(m\angle D=m\angle E=62\)porque son ángulos interiores alternos y las líneas son paralelas. \(m\angle C=m\angle A=28\)porque son ángulos interiores alternos y las líneas son paralelas. \(m\angle DBC=m\angle ABE=90\)porque son ángulos verticales.
Ejemplo\(\PageIndex{3}\)
Determinar la medida de los ángulos faltantes.
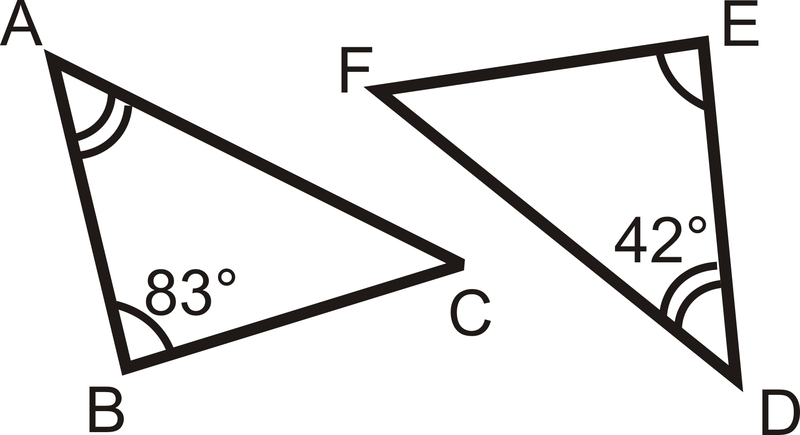
Solución
Desde el Teorema del Tercer Ángulo, lo sabemos\(\angle C\cong \angle F\). Del teorema de la suma del triángulo, sabemos que la suma de los ángulos interiores en cada triángulo es\(180^{\circ}\).
\(\begin{align*} m\angle A+m\angle B+m\angle C &=180^{\circ} \\ m\angle D+m\angle B+m\angle C=180^{\circ} \\ 42^{\circ}+83^{\circ}+m\angle C &=180^{\circ}\\ m\angle C &=55^{\circ}=m\angle F\end{align*}\)
Ejemplo\(\PageIndex{4}\)
Explicar por qué funciona el Teorema del Tercer Ángulo.
Solución
El Teorema del Tercer Ángulo es realmente como una extensión del Teorema de la Suma del Triángulo. Una vez que conoces dos ángulos en un triángulo, automáticamente conoces el tercero por el Teorema de la Suma del Triángulo. Esto significa que si tienes dos triángulos con dos pares de ángulos congruentes entre ellos, cuando usas el Teorema de la Suma del Triángulo en cada triángulo para llegar al tercer ángulo obtendrás la misma respuesta ambas veces. Por lo tanto, el tercer par de ángulos también debe ser congruente.
Ejemplo\(\PageIndex{5}\)
Determine la medida de todos los ángulos en el triángulo:
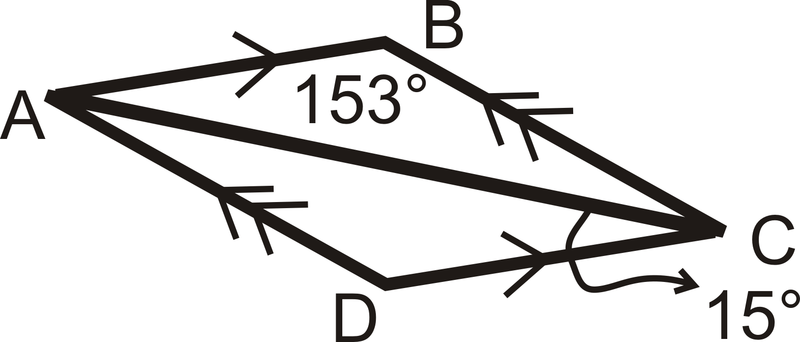
Solución
Primero podemos ver eso\(m\angle DCA=15^{\circ}\). Esto significa que\(m\angle BAC=15^{\circ}\) también porque son ángulos interiores alternos. \(m\angle ABC=153^{\circ}\)fue dado. Esto significa por el Teorema de la Suma Triangular que\(m\angle BCA=12^{\circ}\). Esto significa que\(m\angle CAD=12^{\circ}\) también porque son ángulos interiores alternos. Por último,\(m\angle ADC=153^{\circ}\) por el Teorema de la suma del triángulo.
Revisar
Determinar las medidas de los ángulos desconocidos.
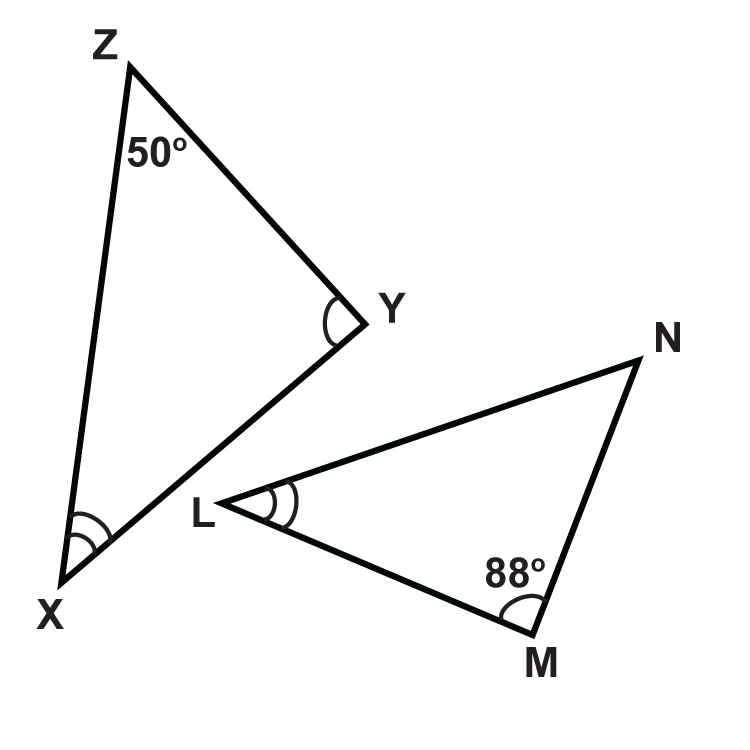
- \(\angle Y\)
- \(\angle x\)
- \(\angle N\)
- \(\angle L\)
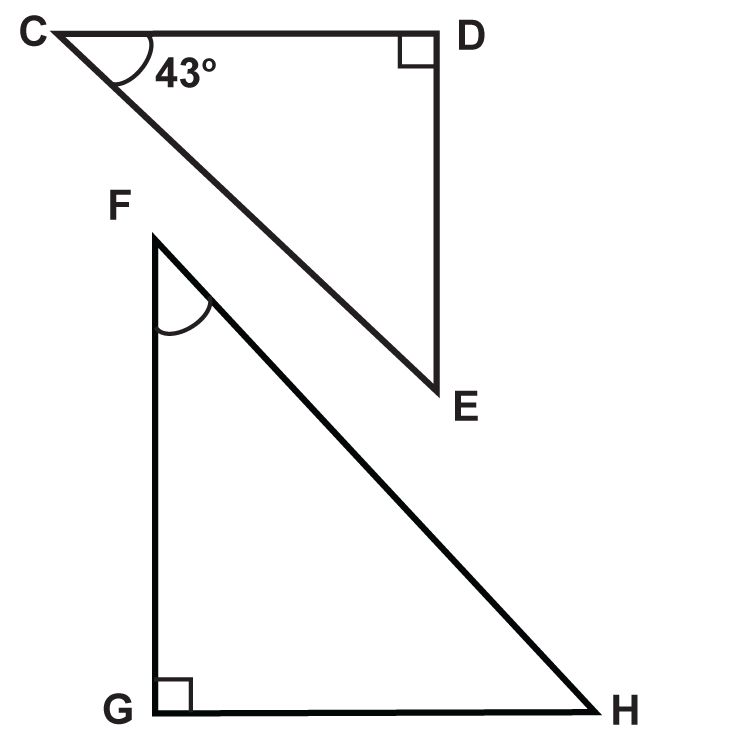
- \(\angle E\)
- \(\angle F\)
- \(\angle H\)
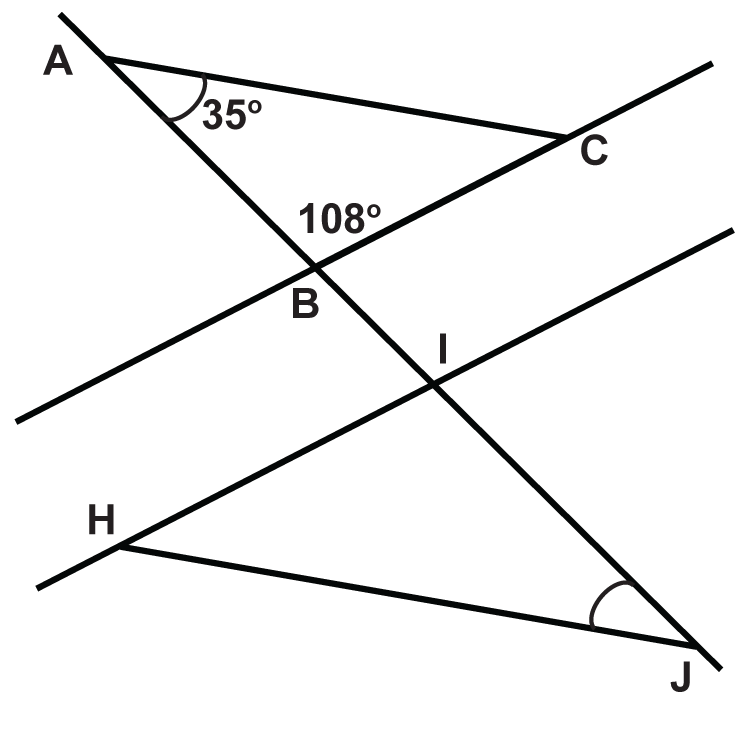
Eso se puede asumir\(\overleftrightarrow{BC}\parallel\overleftrightarrow{HI}\).
- \(\angle ACB\)
- \(\angle HIJ\)
- \(\angle HJI\)
- \(\angle IHJ\)
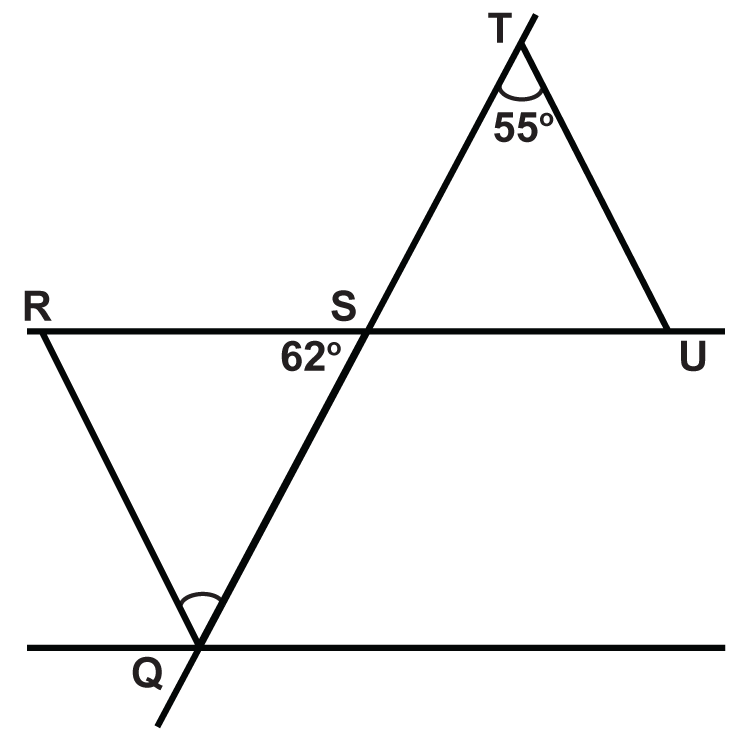
- \(\angle RQS\)
- \(\angle SRQ\)
- \(\angle TSU\)
- \(\angle TUS\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.5.
El vocabulario
| Término | Definición |
|---|---|
| Teorema de suma de triángulo | El Teorema de la Suma del Triángulo establece que la medida de los tres ángulos interiores de cualquier triángulo se sumará\(180^{\circ}\). |
| Teorema del Tercer Ángulo | Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces el tercer par de ángulos también es congruente. |
Recursos adicionales
Video: Principios del Teorema del Tercer Ángulo - Básico
Actividades: Preguntas de discusión del teorema del tercer ángulo
Ayudas de estudio: Guía de estudio de congruencia triangular
Práctica: Teorema del Tercer Ángulo
Mundo Real: Teorema del Tercer Ángulo
- \(\angle RQS\)
- \(\angle SRQ\)
- \(\angle TSU\)
- \(\angle TUS\)